LUT = lookup table

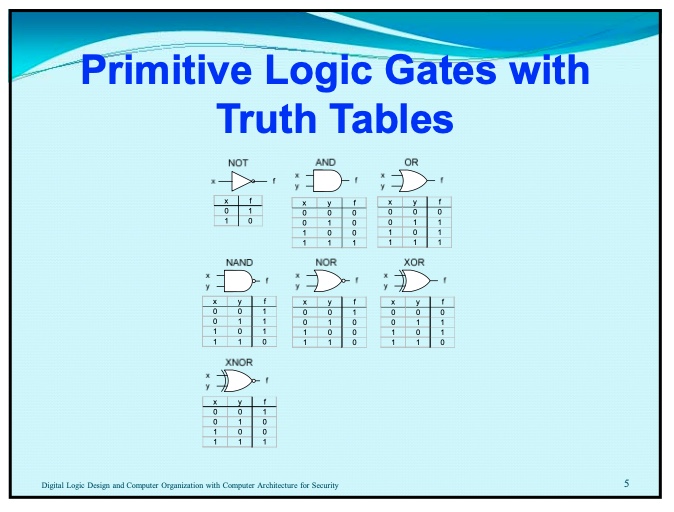
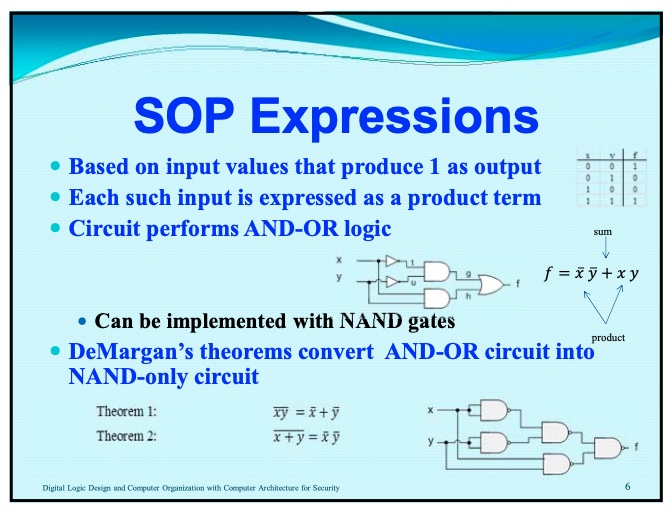
SOP = sum of products
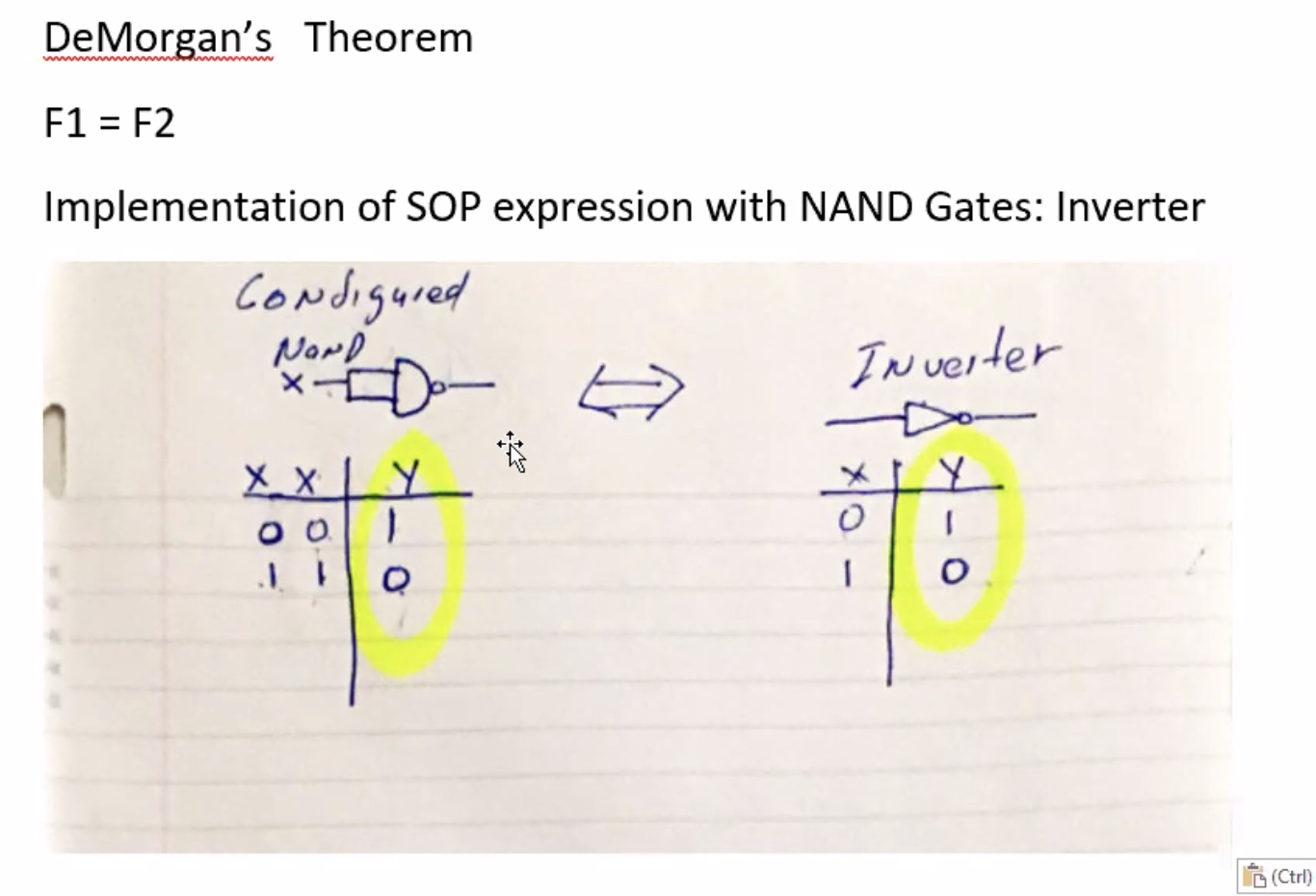
DeMorgan’s theorem #
- Two or more variables NAND’d together is the same as the two terms inverted and OR’d
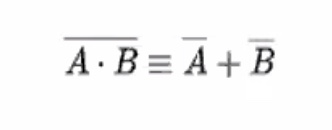
- Two or more variables NOR’d together is the same as the two variables inverted and AND’d together
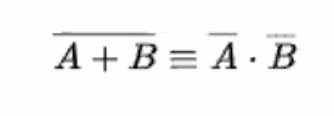
Lets show this via tables for these two equations:
\[\begin{aligned} F1 &= F2 \\ \neg(A \cdot B) &= \neg A + \neg B \end{aligned}\]Here is a table for \(F1\) :
| \(A B\) | \(A \cdot B\) | \(\neg(A \cdot B)\) |
|---|---|---|
0 0 |
0 |
1 |
0 1 |
0 |
1 |
1 0 |
0 |
1 |
1 1 |
1 |
0 |
Here is a table for \(F2\) :
| \(A B\) | \(\neg A \neg B\) | \(\neg A + \neg B\) |
|---|---|---|
0 0 |
1 1 |
1 |
0 1 |
1 0 |
1 |
1 0 |
0 1 |
1 |
1 1 |
0 0 |
0 |
Notice that the output of each table is the same, thus the theorem is true.