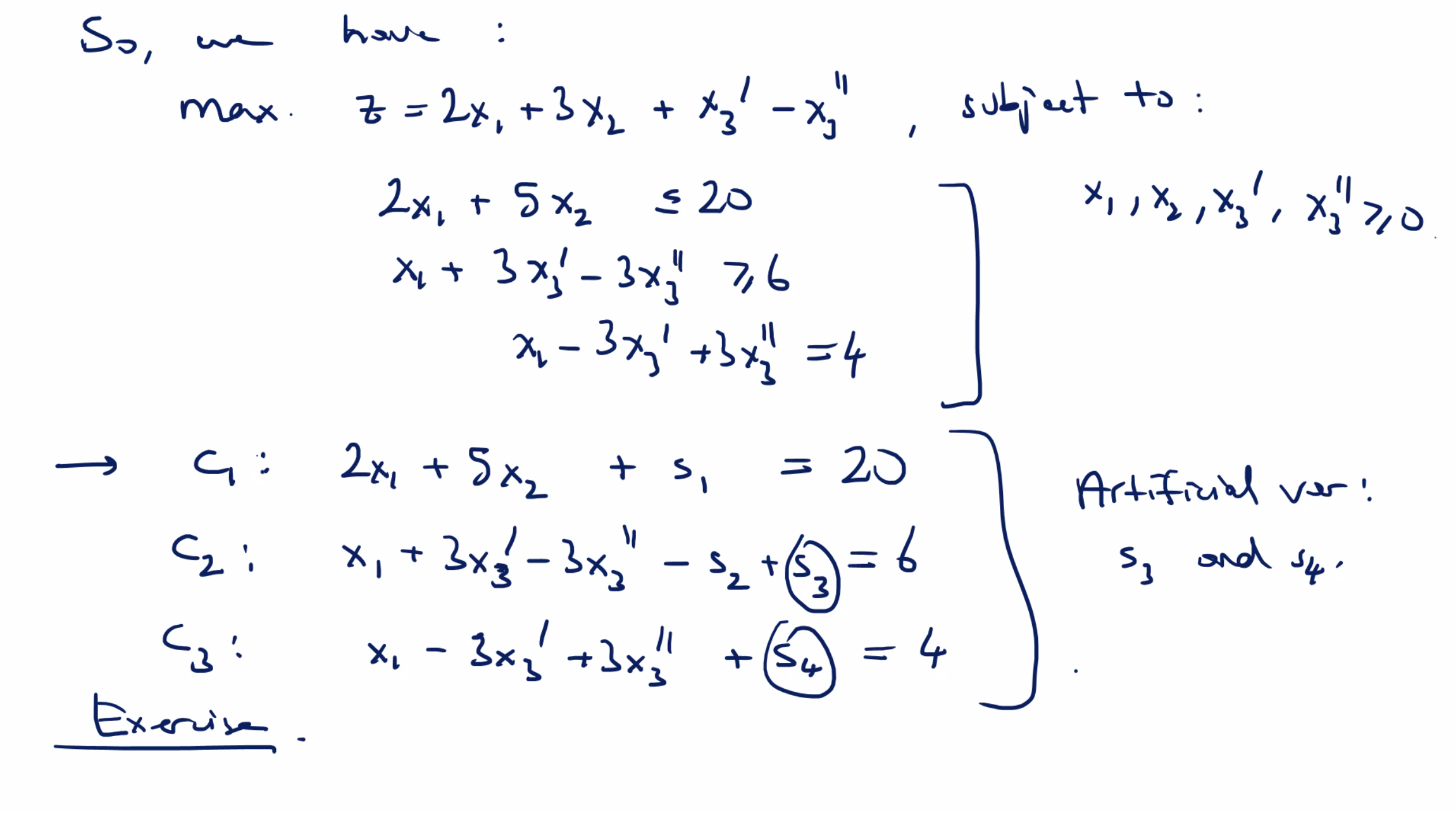Duality cont. #

• and \( A \to A^T \)

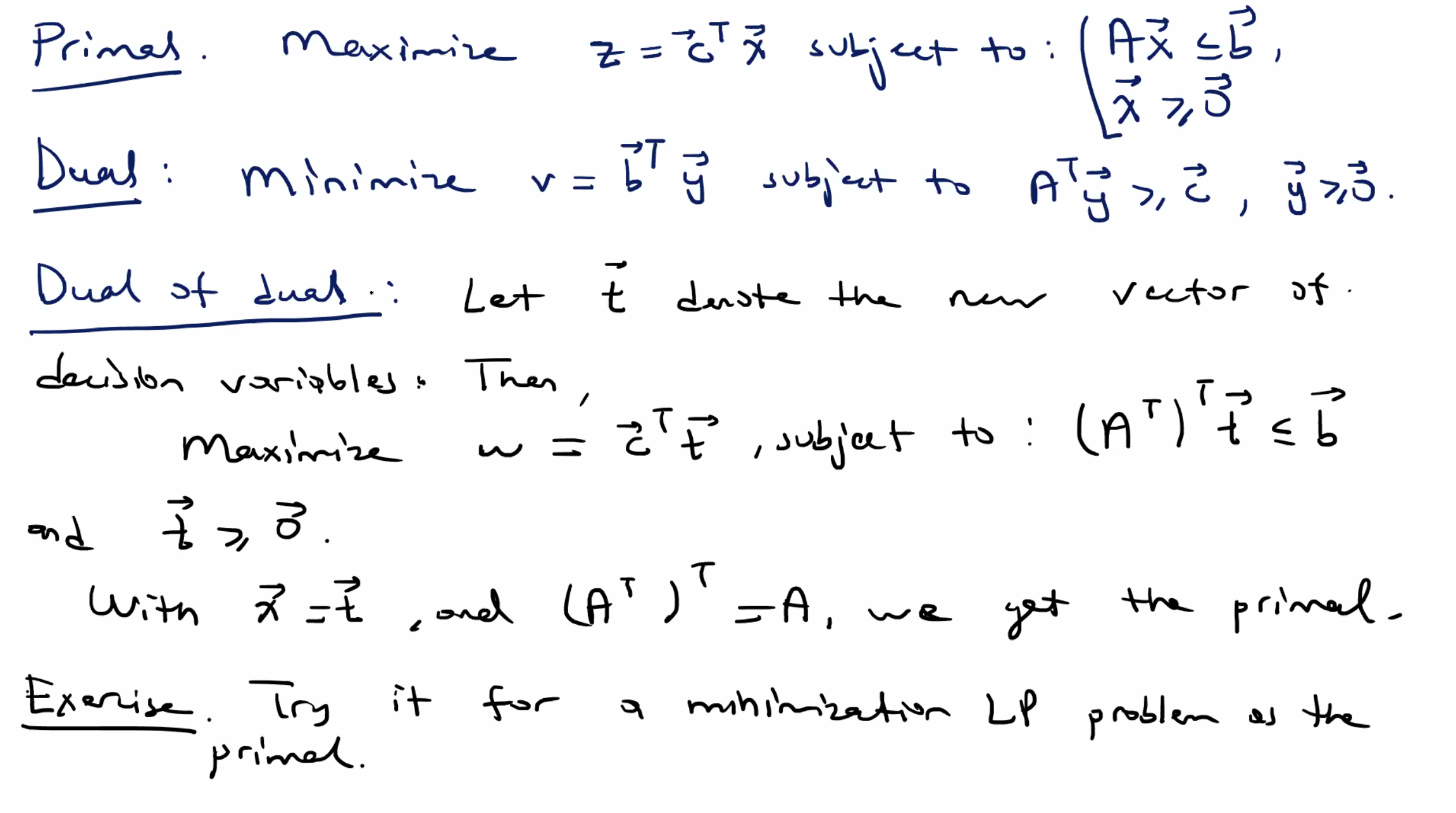
Facts, properties, principals #

1. Observe that there is a connection between shadow prices and the dual problem. An optimal solution to the symmetric dual of a primal LP problem
2. Let \( \hat{x} \) be a feasible solution to a primal problem in normal form with objective function \[ z = \bar{C}^T \bar{x} \] Let \( \hat{y} \) be a feasible solution to its symmetric dual problem with the objective function \[ v=\bar{b}^T \bar{y} \] Let \[ \hat{z} = \bar{C}^T \bar{x} \] and \[ \hat{v} = \bar{b}^T \hat{y} \] If \( \hat{z} = \hat{v} \) , then \( \hat{x} \) and \( \hat{y} \) are optimal solutions to their respective LP problem, and \( \hat{z} = \hat{v} \) is the optimal value for both problems. This is called the Optimality Principle.
3. Strong Duality Principle: If an optimal solution exists to either primal or dual, the other problem also has an optimal solution and the optimal values for both problems are equal to each other.

What if some of the constraints are not in normal form? #

If our constraints are not in the normal form in the primal LP problem, then we can transform them into a normal form.

For example,

• if a constraint \( C_j \) in a maximization problem has a “ \( \geq \) ” type inequality, we multiple by sides by \( -1 \) to convert it to a “ \( \leq \) ” type inequality.
• if a constraint \( C_j \) in a minimization problem has a “ \( \leq \) ” type inequality, we do the same as above

For equality constraints:

• we need to replace an inequality with two inequalities to make it a constraint in a “normal” form for duality purposes.
• for a maximization problem, if we have a constraint \[C_j : a_1 x_2 + a_2 x_2 = K \] which is equivalent to \[ a_1 x_2 + a_2 x_2 \leq K \\ a_1 x_1 + a_2 x_2 \geq K \] we can multiply the second one by \( -1 \) so everything is “ \( \leq \) ”. So, our new constraint \( C_j \) is \[\begin{aligned} C_j'&: &a_1 x_1 + &a_2 x_2 &\leq &K \\ C_j''&: &-a_1 x_1 - &a_2 x_2 &\leq &-K \end{aligned}\]
• for a minimization problem, convert both constraints to a “ \( \geq \) ” in a similar manner.
• another approach is to introduce “free” variables and create variables unrestricted in sign to control its dimension.

An example #

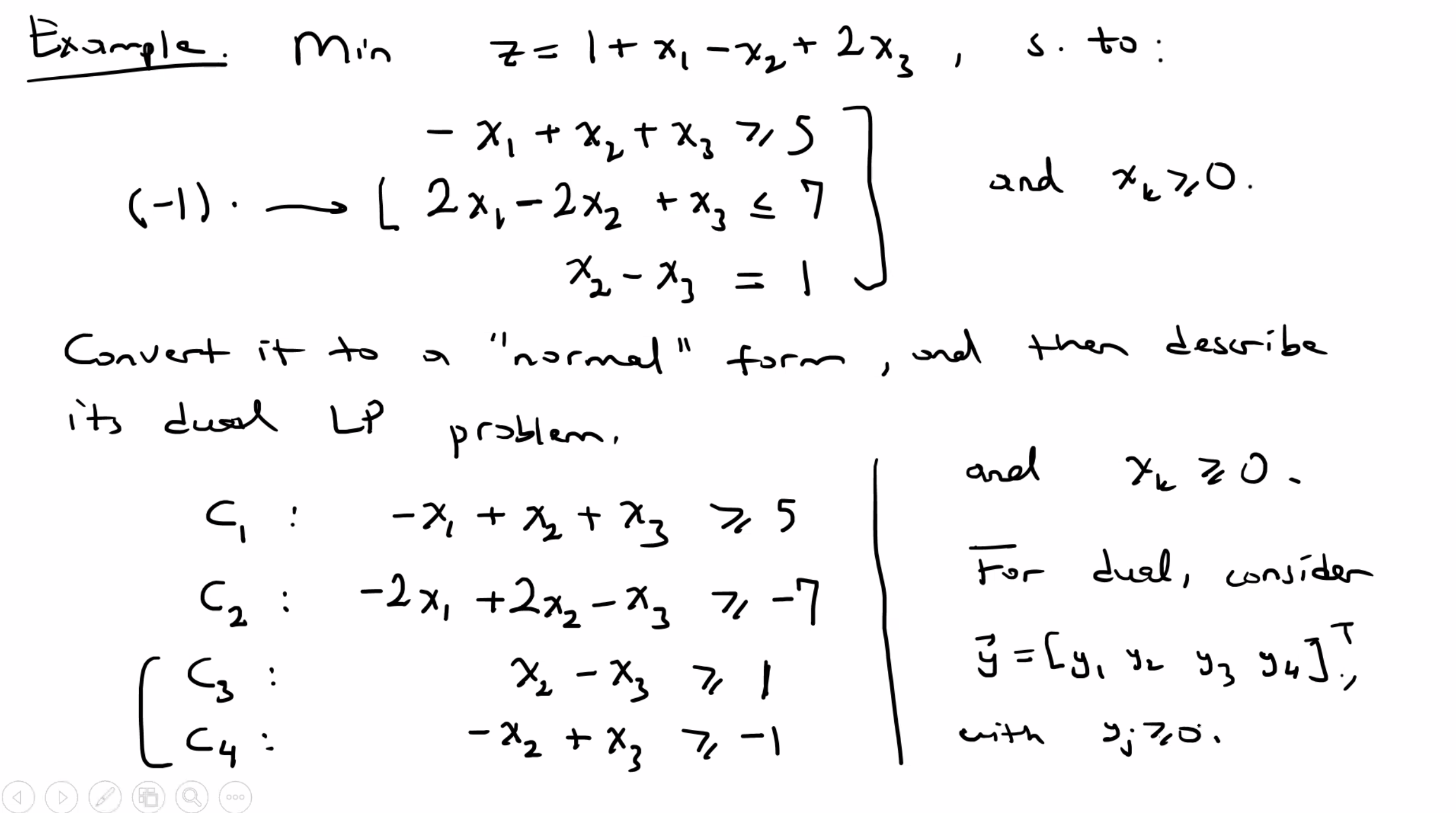
Lets convert it to canonical form:

Another example #