Asymptotic notation cont #
Big Omega #
Omega is lower bound (where Big O is upper bound).
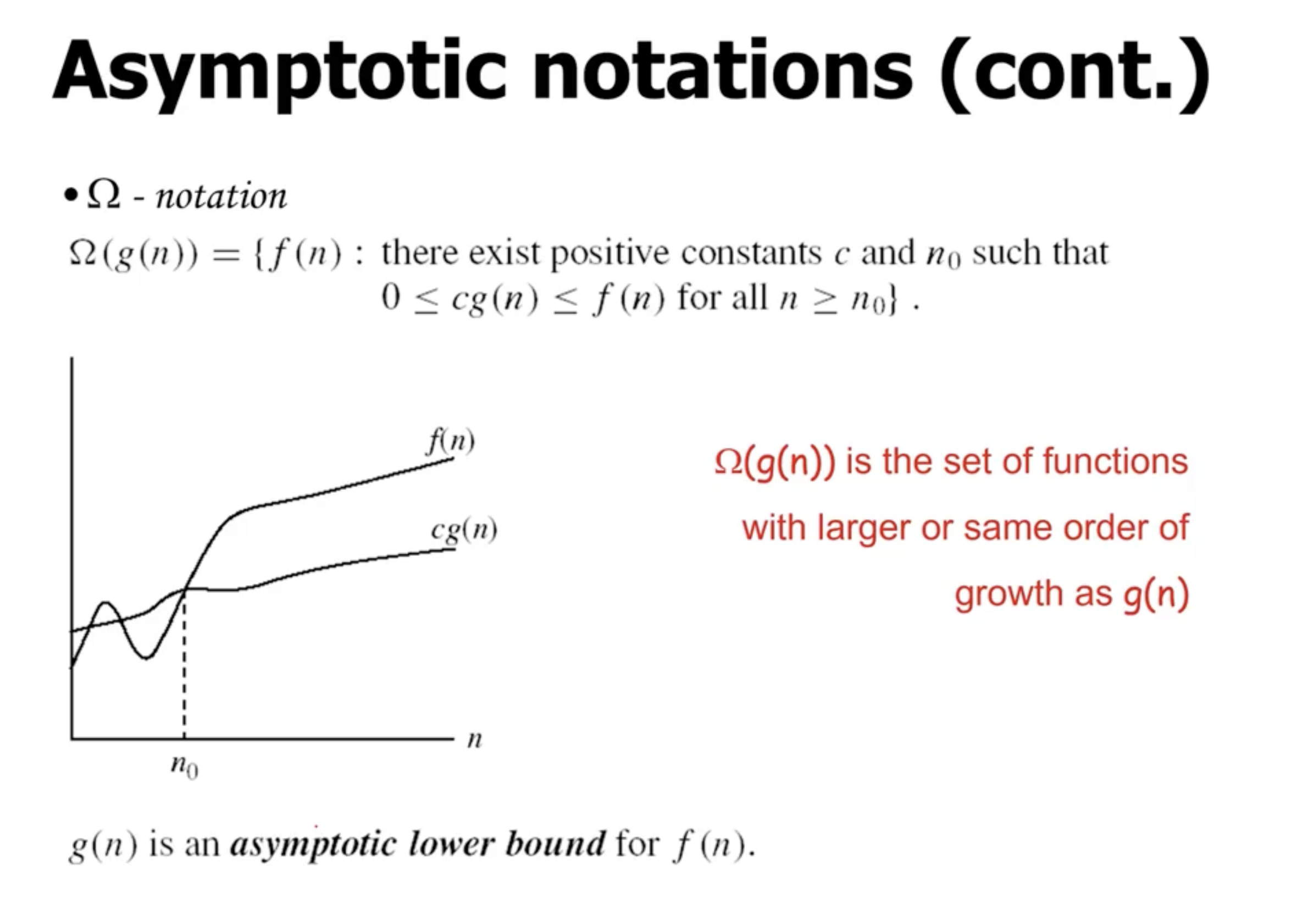
Examples #
\[\begin{aligned} 5n^2 = \Omega(n) \end{aligned}\] \( \exists c,n_0 \) such that \( 0 \leq c_n \leq 5 n^2 \) So, \[\begin{aligned} c \leq 5n \end{aligned}\] so \( c = 1 \) and \( n_0 = 1 \) .
\[\begin{aligned} 100n + 5 \neq \Omega (n^2) \end{aligned}\]
\( \exists c, n_0 \) such that \( 0 \leq cn^2 \leq 100n + 5 \)
\[\begin{aligned} 100n + 5 &\leq 100n + 5n (\forall n \geq 1) = 105n \\ cn^2 &\leq 105n \\ &\Rightarrow n(cn - 105) \leq 0 \end{aligned}\]Since \( n \) is positive, \( cn - 105 \leq 0 \Rightarrow n \leq \frac{105}{c} \) . This is not possible to satisfy, because \( n \) can be arbitrarily large and go to infinity. \( n \) can not be smaller than a constant!
\[\begin{aligned} n = \Omega (2n) \end{aligned}\]
\( \exists c,n_0 \) such that \( 0 \leq c 2n \leq n \)
\[\begin{aligned} c 2n &\leq n \\ 2c &\leq 1 \\ c &\leq \frac{1}{2} \end{aligned}\]Big Theta #
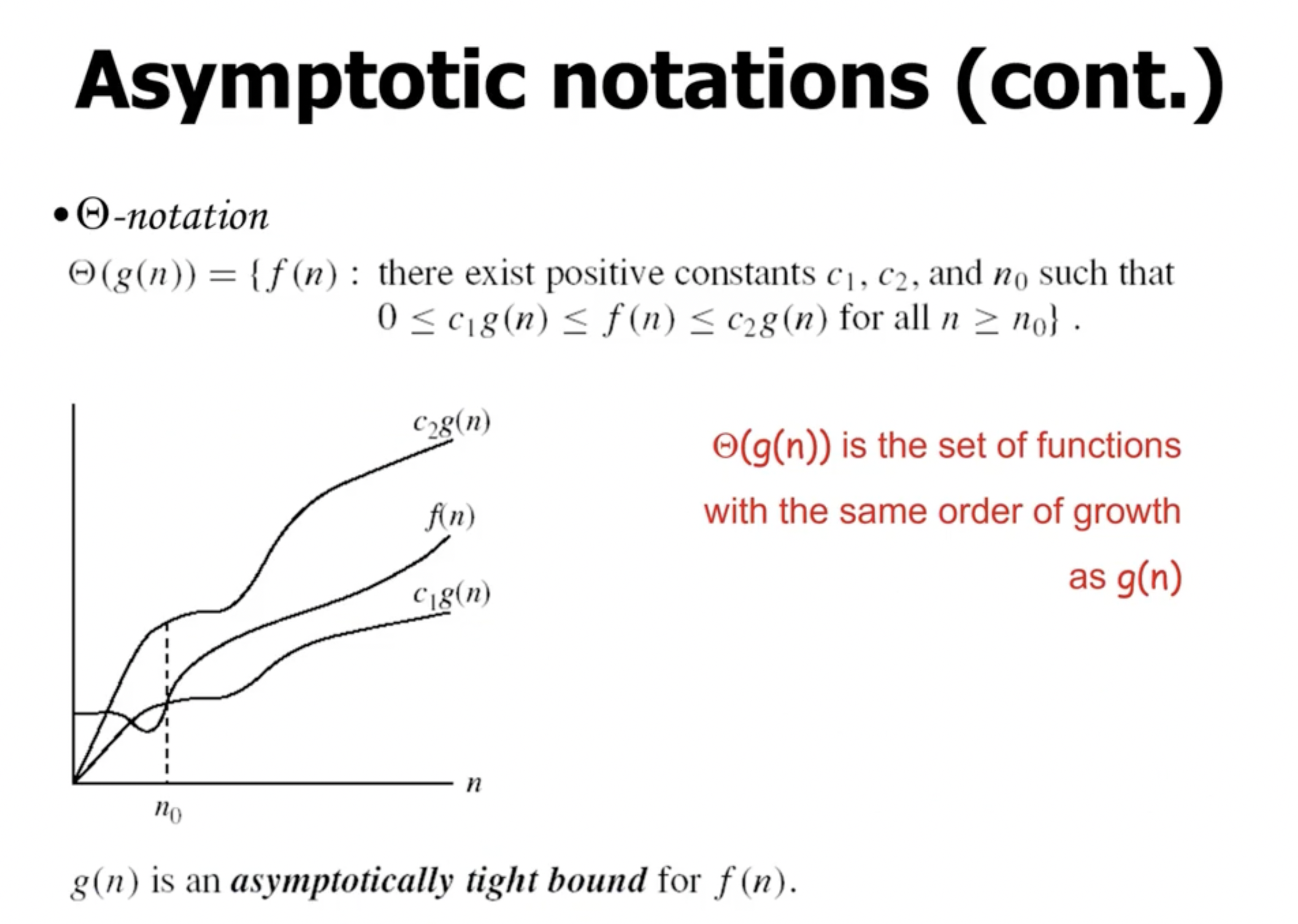
Big \( \Theta \) is both Big \( O \) and Big \( \Omega \) .
When finding \( n_0 \) we usually find it via \[\begin{aligned} n_0 = \text{max}(n_0^O, n_0^\Omega) \end{aligned}\]
Examples #
\[\begin{aligned} \frac{n^2}{2} - \frac{n}{2} = \Theta(n^2) \end{aligned}\]So, we can first prove that it is \( O(n^2) \) :
\[\begin{aligned} \frac{1}{2}n^2 - \frac{1}{2}n \leq n^2 \forall n \geq 0 \end{aligned}\] where \( c_2 = \frac{1}{2} \) and \( n_0 \geq 0 \) .
We can then prove that it is \( \Omega(n^2) \) :
\[\begin{aligned} \frac{1}{2}n^2 - \frac{1}{2} n &\geq \frac{1}{2}n^2 - \frac{1}{2} n \cdot \left( \frac{1}{2} n \right) \\ & = \frac{1}{4} n^2 \end{aligned}\] where \( c_1 = \frac{1}{4} \) and \( n_0 \geq 2 \) .
So for our Big \( \Theta \) problem, \( n_0 = \text{max} (0,2) = 2 \) .
When we try to solve something like \( n \neq \Theta (n^2) \) , we can see there is a contradiction:
\[\begin{aligned} c_1 n^2 \leq n \leq c_2 n^2 \end{aligned}\]Note: Whenever we get something where \( n \leq c \) , we can tell there will be a contradiction, because \( n \to \infty \) .

Relations between different sets #
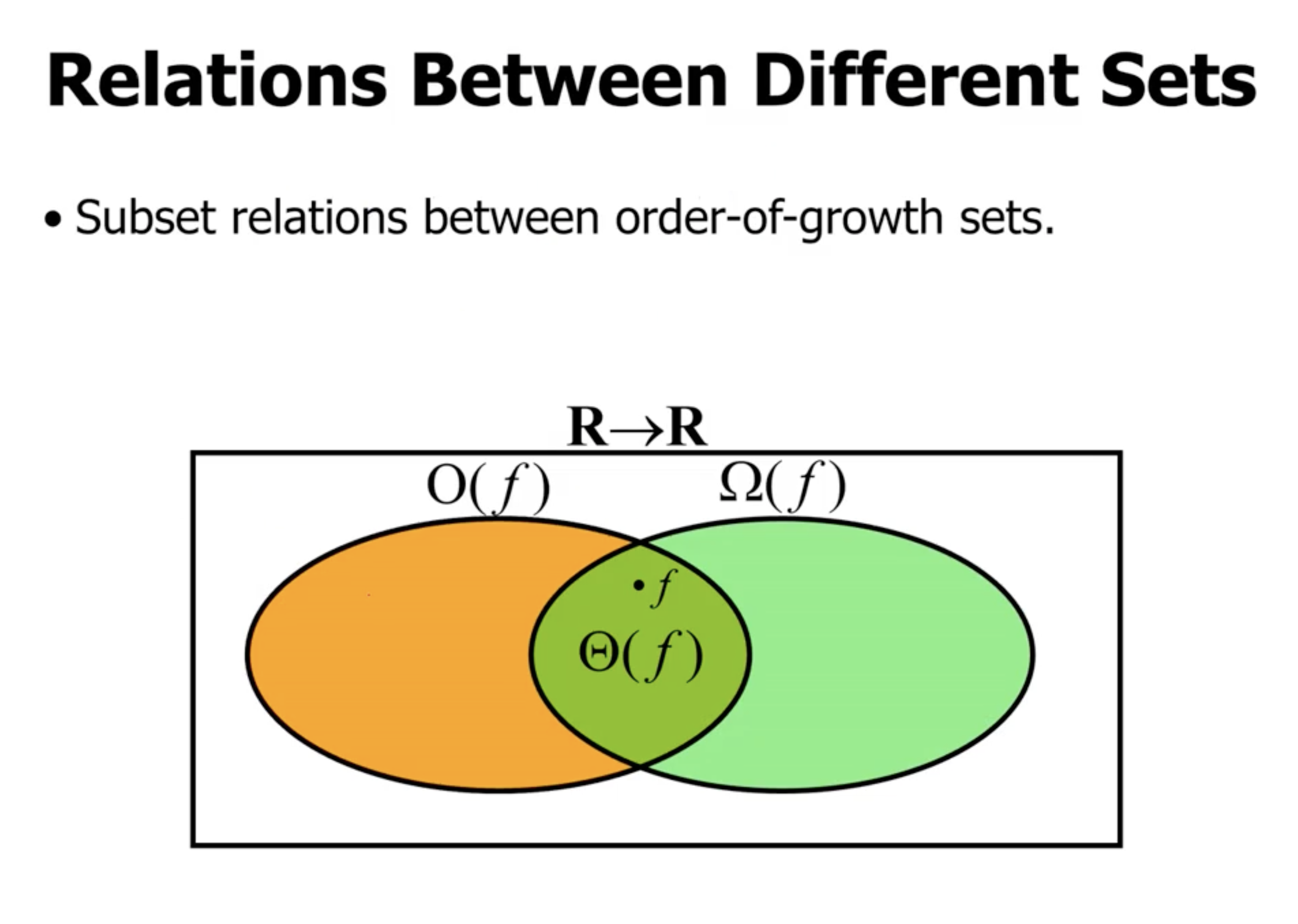
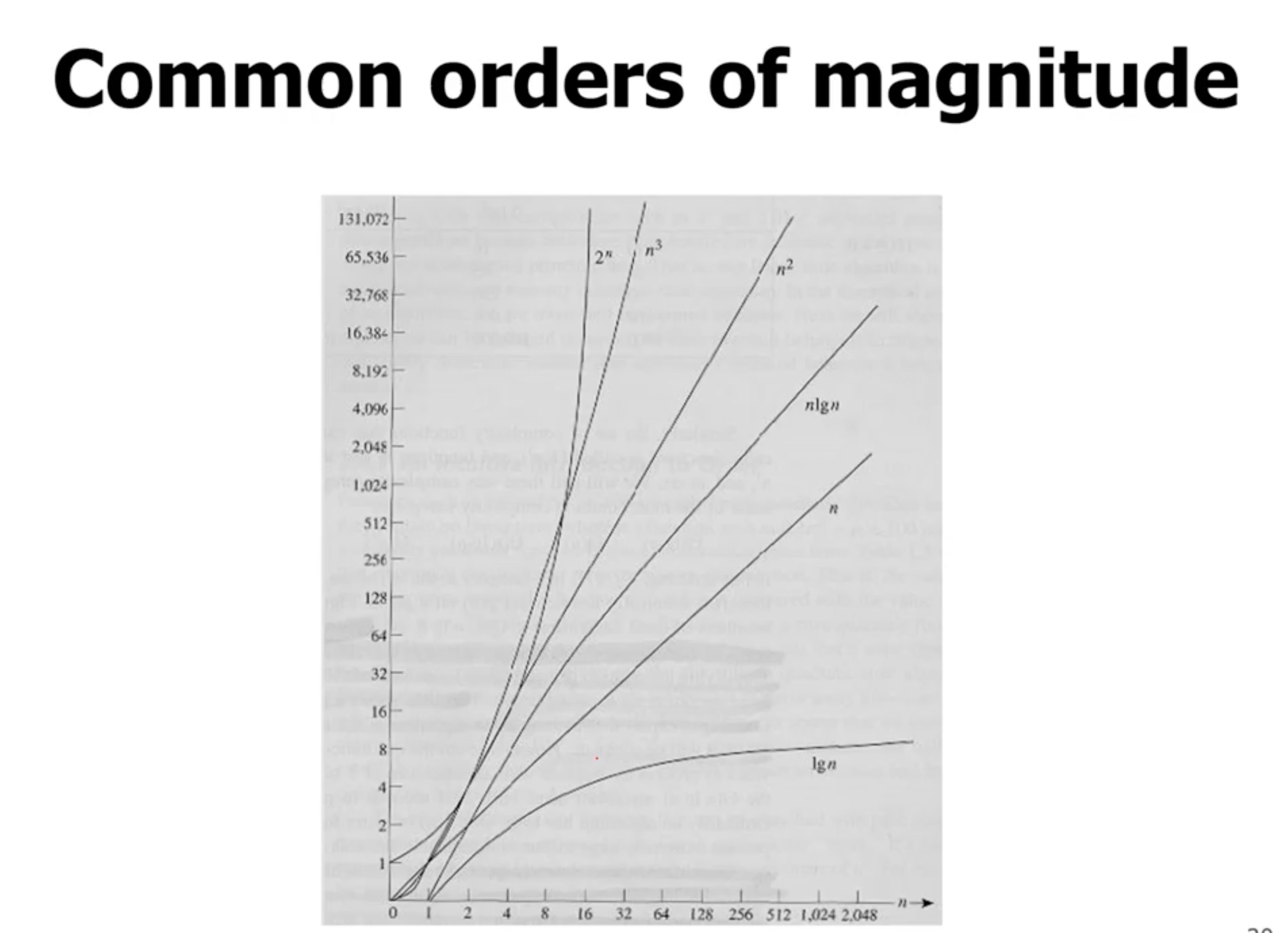
Note: Factorial terms like \( n! \) are even worse than \( 2^n \) .
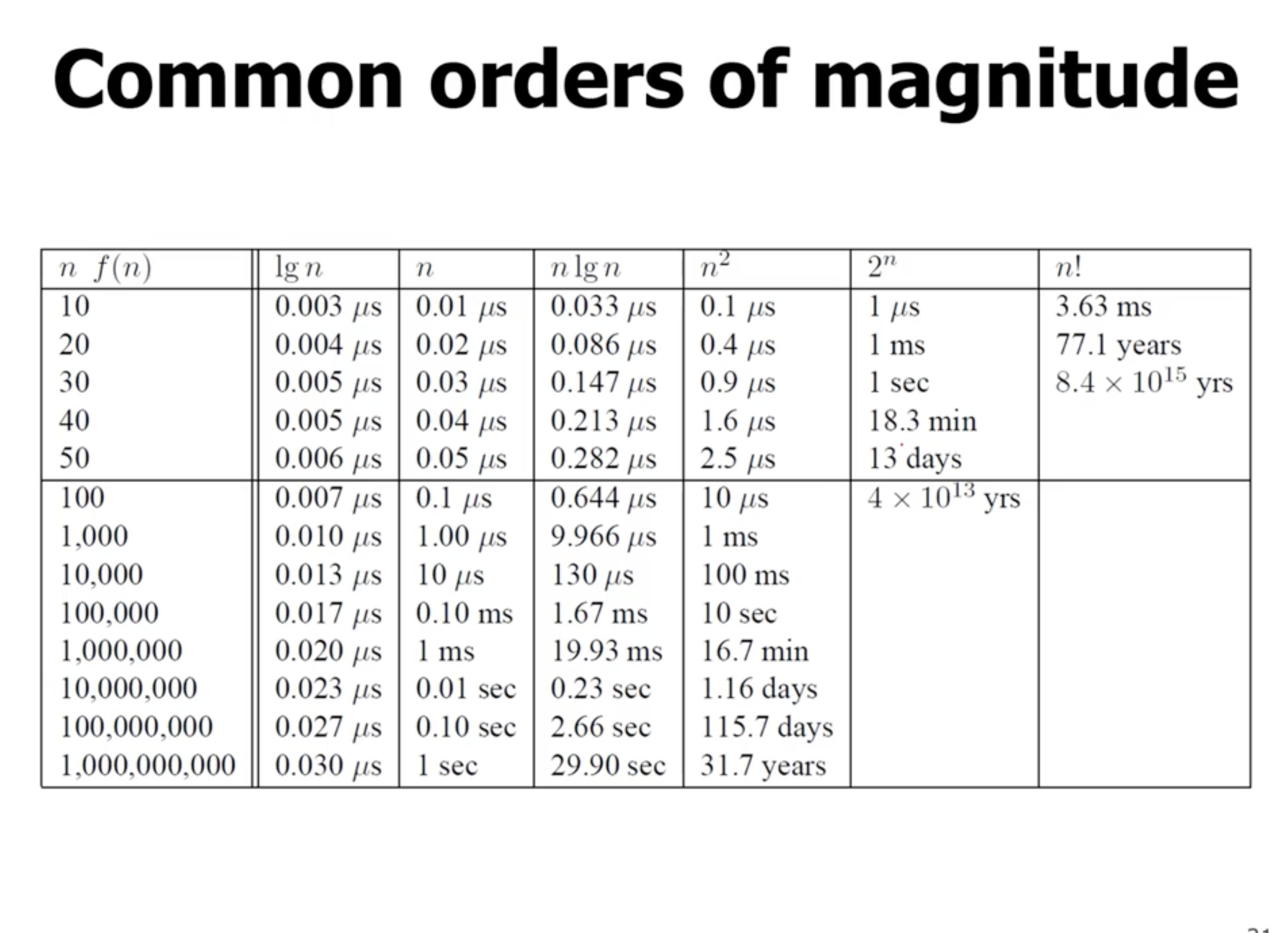

When we talk about the complexity of an algorithm, it doesn’t matter what base we use when we talk about logarithmic growth. This is because we can simply change the bases to anything using the change of base formula (as long as the base is not in the exponent).
More examples #

Asymptotic properties #


Common summations #

Mathematical induction #


Remember
- Find the base case
- In the inductive step, try to find the \( S(n) \) case inside the \( S(n+1) \) case.