Acceptance algorithm #

Decision problems #

A decision problem is a problem that has a binary answer, true or false (or accept and reject). A decision problem may be something like: “given \( x \) , is \( x \) prime?” We can use decision problems to prove the limitations for Turing machines, because there isn’t a pumping lemma for Turing machines.

If we can show that a decision problem can’t be solved, then we can show that computers can’t solve the same problem.

Consider this theorem: There is no algorithm accept(m,x), where m is another algorithm and x is an input, that for every m and x returns true if m outputs “accept” for x and “reject” otherwise.

Why not? Why don’t we just try to run the algorithm m on the input x?

accept(m,x):
    tmp = m(x)
    if tmp == "accept":
        return true
    return false

What if m takes a long time? For m to output “accept” it has to finish its computation and output. The complement of that is that it doesn’t return “accept”, OR it doesn’t finish its computation (infinte loop). If m is still running, we don’t know if its going to halt and accept, halt and reject, or never halt. So, the above pseudocode does not work.

The Towers of Hanoi #

The game where there is 3 pegs, and discs that get shorter and shorter up on the peg. The rule is you can only move one disc at a time, and you can’t put a bigger disc on top of a smaller disc.

There is a strategy for doing this: take all but the biggest disc and move it to the far peg, move the biggest disc to the middle, and move the discs back to the first disc.

This algorithm has a runtime complexity of \( O(2^n) \) . So if the game starts with \( n = 64 \) discs, the runtime is going to take a really long time. There is no algorithmic way to tell whether we are stuck in an infinite loop, or that the algorithm is simply taking a really long time to complete.

A proof sketch to show there isn’t an accept algorithm #

We will assume accept(m,x) exists. Lets define an algorithm D(m), where m is an algorithm:

D(m):
    if accept(m,m):
        output reject
    else:
        output accept

Note: accept(m,m) may look weird, but its really just testing the source code of m on itself. This is similar to a C compiler being written in C (a common test is to see if a C compiler can compile itself and output a functioning compiler).

D(m) is using accept(m,x) as a subroutine. So lets try to use it by running D(D). This would result in this substitution:

D(D):
    if accept(D,D):
        output reject
    else:
        output accept

So if D accepts D, then accept(D,D) is true by definition. But,

• if D accepts D, when we run D(D), accept(D,D) will be true and the output will be “reject.”
• if D doesn’t accept D, it will output “accept.”

These are contradictions.

All of this works because we assume that accept(m,x) exists.

Reductions #

A reduction, in a sense, is a way to say that if one problem isn’t possible, than the other problem isn’t possible also. You see this in NP-complete problems a lot.

Problem A “reduces” to Problem B, if a Problem A Solver could be constructed using a Problem B Solver.

ASolver(a_instance):
    ...
    BSolver
    ...
    returns a_answer

ASolver takes an instance of A, and returns an answer. Notice that ASolver uses the BSolver subroutine. Then it shows that problem A reduces to problem B.

This pseudocode shows that if there exists a BSolver, that implies that there exists an ASolver.

Concrete example #

Consider a function that finds the median from an array of numbers. Lets assume that the array is odd length so the median is well defined.

FindMedian(arr):
    sorted_array = sort(arr)
    ans = sorted_array[len(arr) / 2]
    return ans

Since this FindMedian function is possible, if the sort function is available. That means that FindMedian reduces to sort. So if there exists a sorting algorithm, then there exists a median finder algorithm. \[\begin{aligned} \exists \text{ sort} \to \exists \text{ median} \end{aligned}\]

A more abstract example #

Consider the function GetRich

GetRich():
    lotto = Genie("next lottery winner")
    return lotto

So the algorithm solves the problem of how to get rich, which uses a subroutine that gives the lottery numbers. So GetRich reduces to Genie. \[\begin{aligned} \exists \text{ Genie} \to \exists \text{ GetRich} \end{aligned}\]

Since there is no genie algorithm, we have no way of writing a get rich algorithm.

How to use reductions to show something doesn’t exist #

Recall contrapositives:

This can be represented as a truth table:

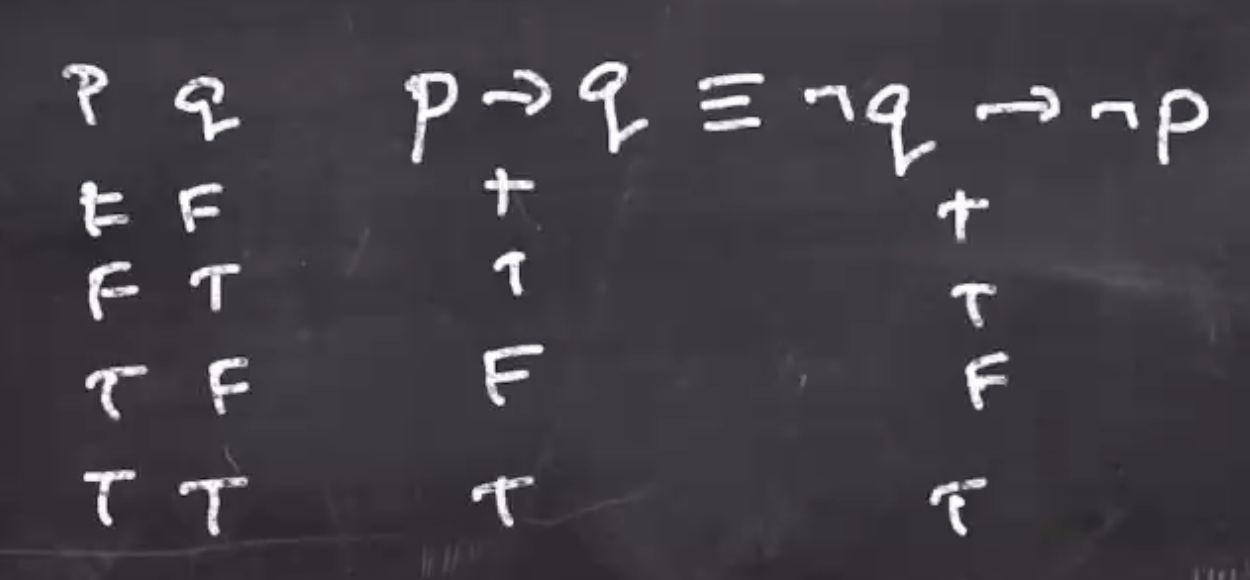
So these 2 statements are logically equivalent.

Since the existence of BSolver implies the existence of ASolver, we can write this as a contrapositive as: “if there does not exists an ASolver, than BSolver doesn’t exist either.”

Acceptance #

Recall: accept(m,x) is trying to output true if algorithm m accepts input x, otherwise false.

We’ve previously established that accept(m,x) is not computable on all (m,x). The reason why this is not possible is because it could go into an infinite loop and never terminate.

To show BSolver cannot exist:

accept(m, x):
    ...
    BSolver
    ...
    return answer

This would show that the existence of BSolver implies the existence of accept, but we are more interested in the contrapositive \[\begin{aligned} \neg \exists \text{ accept} \to \neg \exists \text{ BSolver} \end{aligned}\]

Because accept cannot exist, neither can BSolver.

The Halting problem #

This is possibly the most famous non-computable problem.

halt(m,x) outputs true if m halts on x. m is an algorithm, and x is an input to that algorithm. It can either

• Halt on x and accept
• Halt not on x and reject
• or, get stuck in an infinite loop

We can show this isn’t computable by using our template

accept(m,x):
    if halt(m,x):
        return m(x)
    else:
        return false

If there existed halt(m,x) that worked on all inputs, then accept(m,x) would exist. \[\begin{aligned} \exists \text{ halt(m,x)} \to \exists \text{ accept(m,x)} \end{aligned}\]

But we are interested in the contrapositive: \[\begin{aligned} \neg \exists \text{ accept(m,x)} \to \neg \exists \text{ halt(m,x)} \end{aligned}\]

Since accept(m,x) doesn’t exist on all inputs, halt(m,x) also doesn’t exist.