SQL cont. #

Subqueries can be used inside insert statements:

This insert statement will update the numbers dynamically based on the response from the subquery. The next time an employee is inserted, we can run this insert statement to update DEPTS_INFO using a trigger.

Or, we can use views…

Virtual table view #

CREATE VIEW dept_info_view AS
    SELECT dname,
           COUNT(*) AS no_of_emps,
           SUM(salary) AS total_sal
    FROM department, employee
    WHERE dnumber=dno
    GROUP BY dname;

This results in a self updating table, called a view:

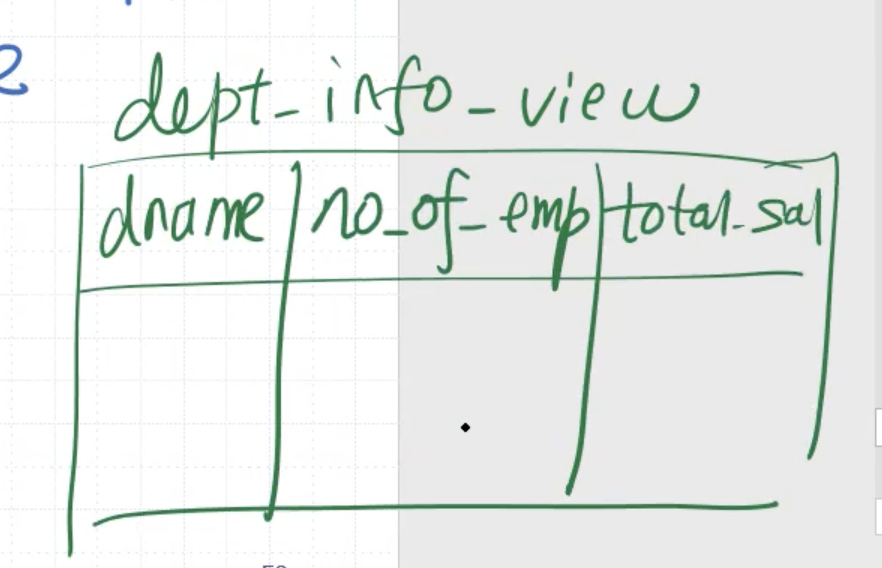
We can query the view the same way we’d query a table.

SELECT * FROM dept_info_view;

The views are maintained by the DBMS. The views will be automatically updated, to main consistency between the view and the table being viewed. This is a way we can have derived attributes.

Note: Views are covered more in depth in CS174.

Functional dependencies and normalization #

File: Normalization slides

Formal measures are also called normal forms. To understand normal forms, we will start with functional dependency.

Functional dependencies #

• \( X \) and \( Y \) are sets of attributes

The functional dependency means that if 2 tuples share the same \( X \) value for an attribute, it means they also share the same \( Y \) value for an attribute.

When \( X \) and \( Y \) are sets of a single item, they may be commonly notated like

So if 2 tuples share the same \( \text{ssn} \) , they will share the same \( \text{ename} \) .

Armstrong’s inferences rules #

• For reflexivity, if \[\begin{aligned} \{\text{ssn}\} \subseteq \{\text{ssn,ename}\} \end{aligned}\] then \[\begin{aligned} \{\text{ssn,ename}\} \to \text{ssn} \end{aligned}\]

• For augmentation, if \[\begin{aligned} \text{ssn} \to \text{ename} \end{aligned}\] we can add something to both sides, and it still holds \[\begin{aligned} \{\text{ssn, address}\} \to \{\text{ename, address}\} \end{aligned}\]

• For transitivity,

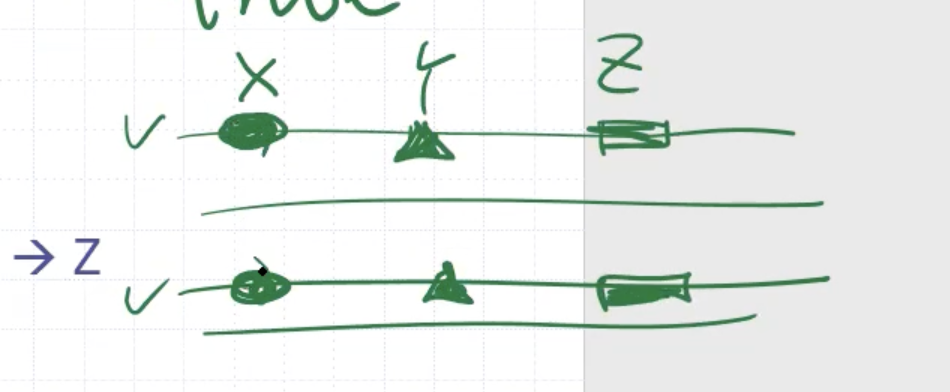
• For decomposition, if \[\begin{aligned} \text{ssn} \to \{\text{ename, bdate, address}\} \end{aligned}\] then we also know \[\begin{aligned} \text{ssn} &\to \text{ename} \\ \text{ssn} &\to \text{bdate} \\ \text{ssn} &\to \text{address} \\ \text{ssn} &\to \{\text{ename, bdate}\} \\ \text{ssn} &\to \{\text{bdate, address}\} \\ \text{ssn} &\to \{\text{ename, address}\} \\ \end{aligned}\]
• Union is the opposite of the decomposition above
• Pseudotransitivity is the transitivity between decomposed sets above

Closure #

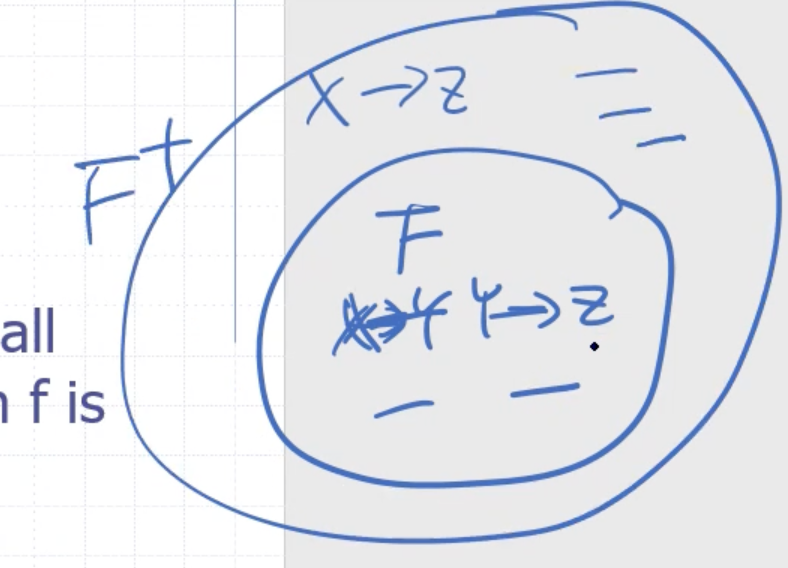
Each element of the set \( F \) is a functional dependency. The set \( F^+ \) is all the dependencies in \( F \) , plus all the dependencies that can be inferred from \( F \) .

The set \( X^+ \) is the set of attributes that are functionally deteremined by \( X \) based on \( F \) .

Equivalence #

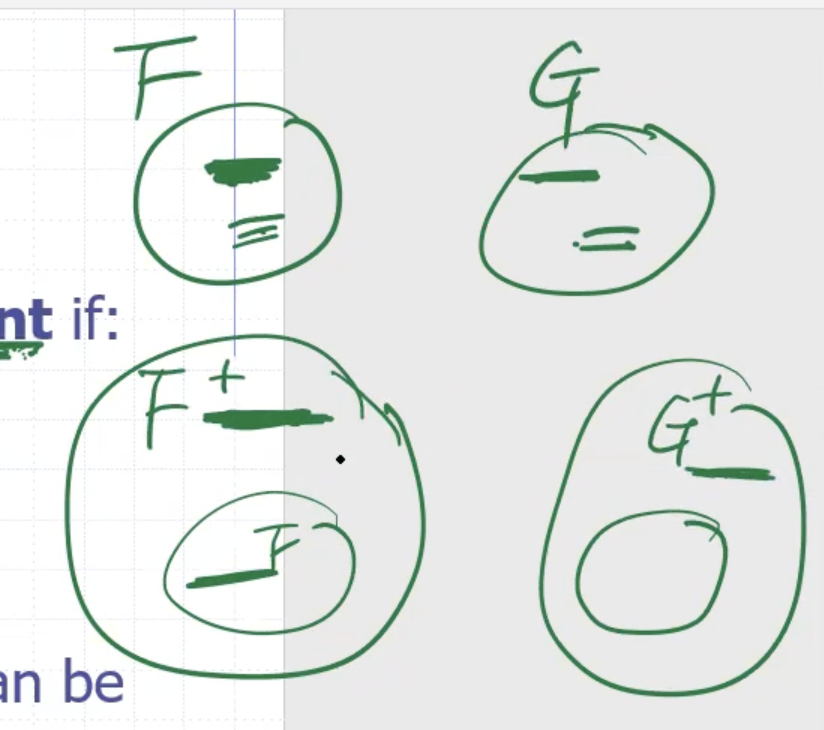
Minimal sets #

Normalization #

There are 4 normal forms we will study: 1NF, 2NF, 3NF, BCNF. The higher the number, the more strict the form.

Keys and superkeys #

• any key is a superkey

First normal form #

Since the Research department has a set of locations, it is not in first normal form. We can put it in first normal form by using decomposition.

• The disadvantage to solution 2 is that the department name and manager’s ssn is repeated for each location.
• The disadvantage to solution 3 is that any tuple that doesn’t have exactly 3 locations will have a lot of null values in the table. Also the schema would needed to be modified if a department needed 4 locations.