Fields #

A field is

• A collection of \( F \) objects
• Two binary operations \( \times \) and \( + \) closed on \( F \) .
• \( F \) contains multiplicative identity 1 where \( (1 \times y) = y \) for all \( y \) in \( F \) .
• \( F \) contains additive identity 0 where \( (0 + y) = y \) for all \( y \) in \( F \) .
• For each \( y \) in \( F \) , there exists a \( z \) in \( F \) such that \( (y + z) = 0 \) (additive inverse).
• For each \( y \) in \( F \) , except 0, there exists a \( z \) in \( F \) such that \( (y \times z) = 1 \) (multiplicative inverse).
• Associative, commutative, distributive laws work as expected

Shorthands

• \( a^{-1} \) is \( a \) ’s multiplicative inverse
• \( -a \) is \( a \) ’s additive inverse
• \( a-b \) is short for \( a + - b \)
• \( a / b \) is short for \( a \times b^{-1} \)

Field examples #

• \( \mathbb{R} \) with standard addition and multiplication form a field (real numbers).
• \( \mathbb{Q} \) with standard addition and multiplication form a field (rational numbers).
• \( \mathbb{Z} \) with standard addition and multiplication doesn’t form a field (integers).
  • \( a^{-1} \) doesn’t exist for most \( a \)
• \( \mathbb{Z}_p \) forms a field with \( p \) prime and addition and multiplication \( \mod p \) .
  • \( p \) must be prime to make sure every element has a multiplicative inverse.

Theorem: If \( p \) is prime, then there is a field of size \( p^n \) for each \( n > 0 \).

\( \mathbb{Z}_p \) is not convenient for high-speed processing: \( \mod p \) is expensive and standard data type don’t hold a prime number of values.

Since 2 is prime, there is a field of size \( 2^n \) for all \( n > 0 \) . This is promising because all data types can hold power-of-two different values.

Galois Fields #

Evariste Galois died age 20 in a duel, 1821

The set of all bit sequences of length \( n \) form a field called \( GF(2^n) \) . Because of the above theorem, there is a guarantee to have a field in a size of \( 2^n \) . We will use \( GF(256) \) for this class.

GF(256) = {00000000, 00000001, 00000010, ..., 11111111}

Addition

• Interpret the bits as coefficients of a degree 7 polynomial with variable \( x \)
• Add the two polynomlials to keep coefficients 0 or 1, mod each coefficient by 2
• Concat the coefficients of the resulting degree 7 polynomial
  • Shortcut, xor’ing the two bytes produces the same result

Multiplication

• Interpret the bits as coefficients of a degree 7 polynomial with variable \( x \)
• Multiply the two polynomials, to keep coefficients 0 or 1, mod each coefficient by 2
• Mod the result by \( x^8 + x^4 + x^3 + x^1 + x^0 \)
• Concat the coefficients of the resulting degree 7 polynomial
  • No shortcut, multiplication is expensive

GF(256) example #

Addition in \( GF(256) \) ,

Multiplication in \( GF(256) \) ,

Note: We are modding by the given polynomial above.

Padding #

Recall that our block cipher modes of operation use blocks of size \( b \) . The more common scenario ends with a block that is less than the size of \( b \) . So we can use padding to help the mode of operation.

In CTR mode, since its producing a key stream, they do not require padding. Stream ciphers do not require padding.

In the other modes, ECB and CBC, we need our input to be a multiple of \( b \) in order for it to work. In a non-stream cipher, to ensure a size that is a multiple of \( b \) , it has to go through a padding process.

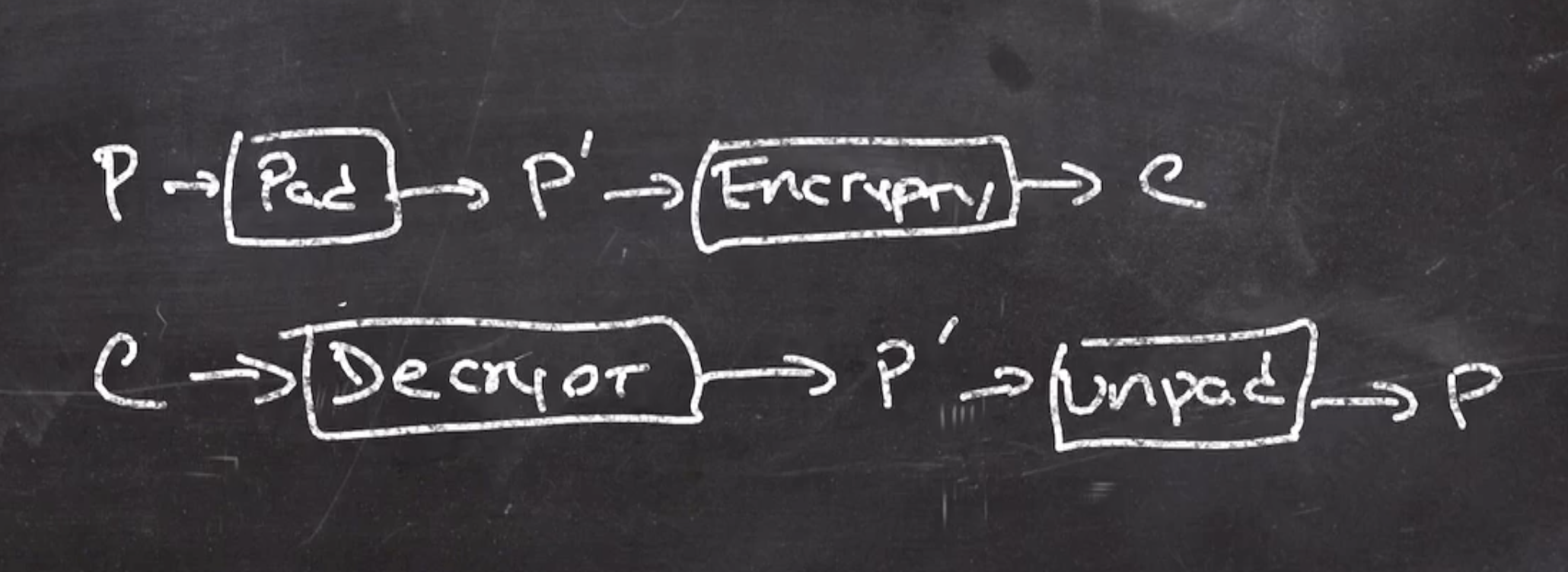
These padding functions need

• unpad is the inverse of pad
• \( P' \) is a multiple of \( b \)
• efficiency

10* padding #

• append a 1 bit, then
• append enough 0 to next multiple of \( b \)

So if \( b = 16 \) ,

b  = 16
p  = 1111 0000 1111         // needs padding to be 16 bits
p' = 1111 0000 1111 1000    // padded

So how do we distinguish between padded and not? We decide to always pad even if it already is a multiple of \( b \) .

So

b  = 16
p  = 1111 0000 1111 0000
p' = 1111 0000 1111 0000 1000 0000 0000 0000

Note: Whenever we do ECB/CBC, we will always apply padding to avoid ambiguity with the receiver.

To unpad

• We will decrypt the ciphertext to get \( P' \)
• Remove all 0 and strip the rightmost 1

b  = 16
p' = 1111 0000 1111 0000 1000 0000 0000 0000
// strip zeros from right of p'
p' = 1111 0000 1111 0000 1
// strip 1 from right of p' to get p
p  = 1111 0000 1111 0000

If we’re at \( b - 1 \) bits,

p  = 1111 1111 1111 111     // one away from 16
p' = 1111 1111 1111 1111    // adding the 1 made it a multiple of b
                            // no 0s needed