Symmetric encryption #

Files:

• Intro to SSE programming
• https://www.crypto-textbook.com/download/Understanding-Cryptography-Chapter4.pdf

Recall that encryption is to be used for private communication. Before a message is encrypted its called a plaintext, and after its been encrypted its called a ciphertext. The ciphertext is then decrypted to get the plaintext.

Recall that we defined

perm384bc(k, x) = perm384(k xor x) xor k

Remember, perm384 is a public random permutation, so its not enough for secrecy. So we xor before and after with a key. That way, even if the adversary knows whats going in or out, the adversary does not know the actual value going into the known algorithm because of the xor with the key.

This is a block cipher (hence the bc in the name perm384bc). All hardware has specific circuits for block ciphers. The standardized block cipher is called AES. It is so standardized that chip builders have specific hardware and assembly instructions to make AES as efficient as possible.

Block ciphers #

A block cipher is defined as

Property: a block cipher with a random key is indistinguishable from a random permutation.

Block cipher modes of operation #

There are multiple modes that we will study.

Consider \( P: \{0,1\}^b \to \{0,1\}^b \) where \( b = 128 \) (blocksize).

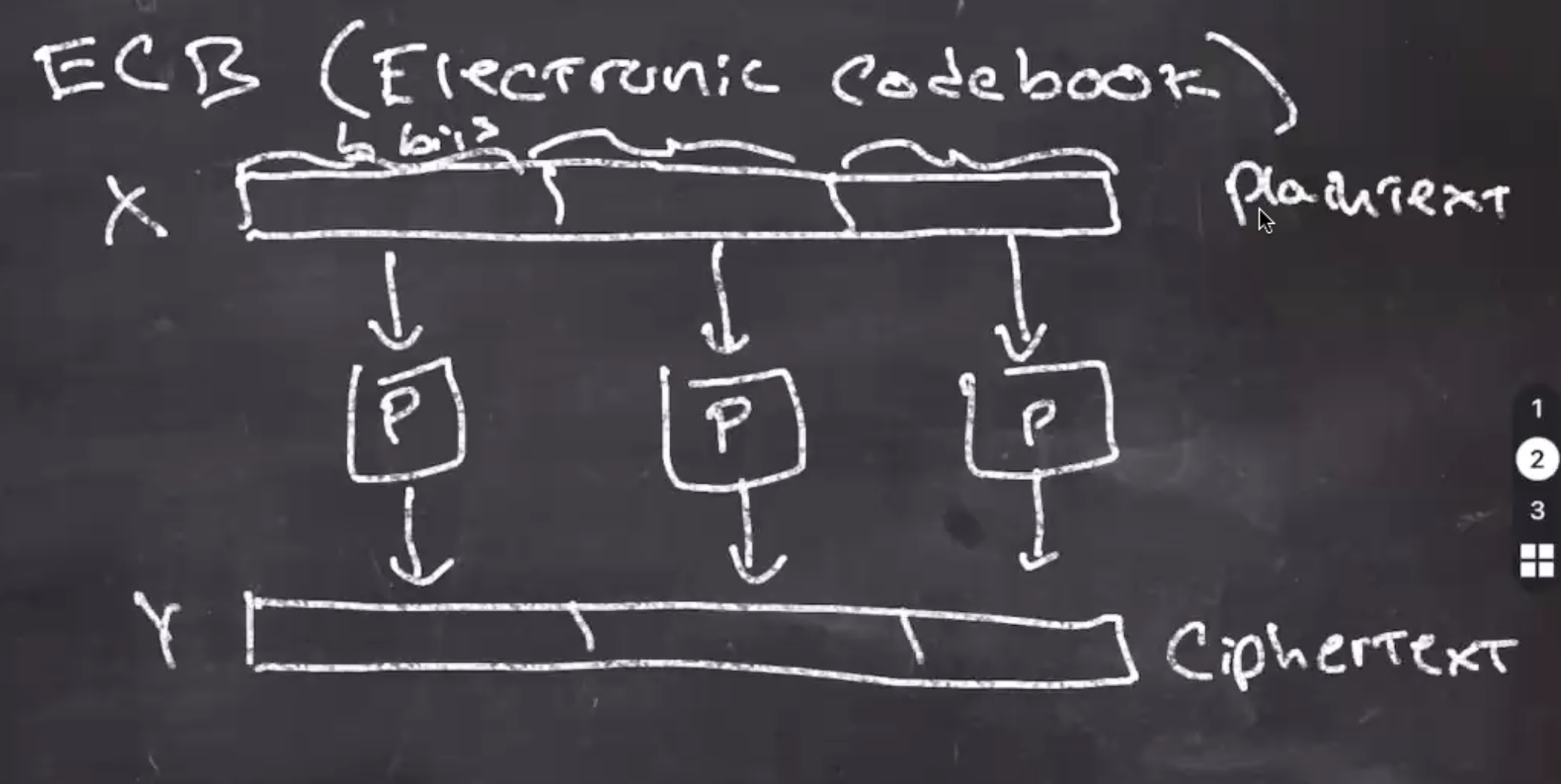
ECB (electronic codebook)

• Let our plaintext be \( x \) , and divided into \( b \) bit size chunks.
• Each chunk will be fed through \( p \)

CBC (cipher block chaining)

• Very similar looking to ECB, but addresses some of ECB’s flaws, eg
  • We want repeated encryption on ciphertexts to be different, so as to not leak information
• Xor an initialization vector \( IV \) , before the block cipher, where \( IV \) is a random \( b \) bits, per encryption.
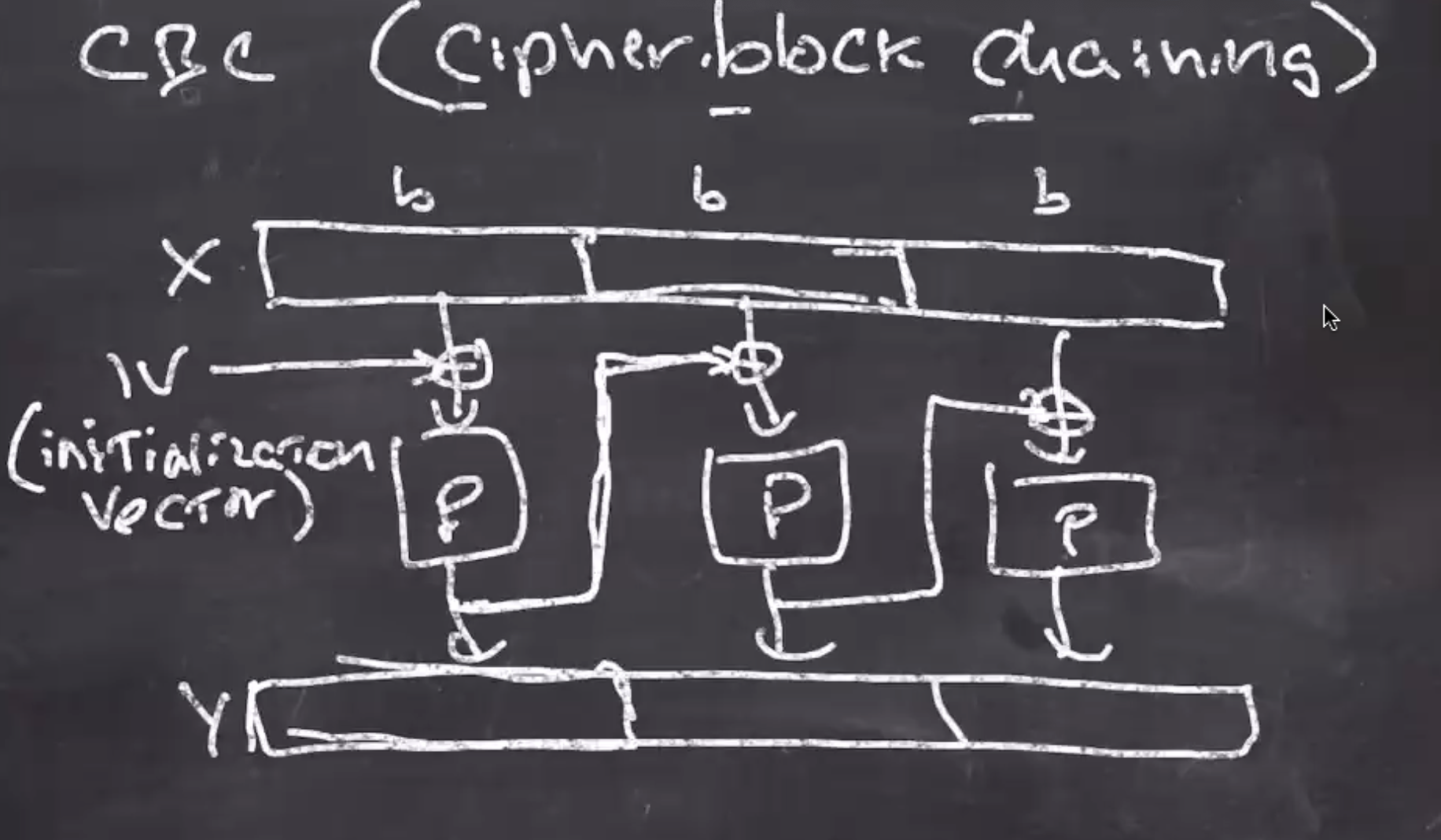
• \( IV \) and the ciphertext \( Y \) are sent to the recipient ( \( IV \) is only used to decrypt the very first block)
• CBC is serial during encryption (blocks are encrypted in order because the second block needs the first and so on)
• However, decryption can be done in parallel

CTR (counter)

• Counter mode behaves differently than the last 2
• Let \( N \) be a nonce (a value used once)
• We build a \( b \) bit block where the first part is \( N \) and the second part is the number 1 encoded into binary (its traditional to have the first block split in half).
• The next block will have the nonce and the number 2 (in binary) as the second part of the block,
• What comes out of this process is the key stream, 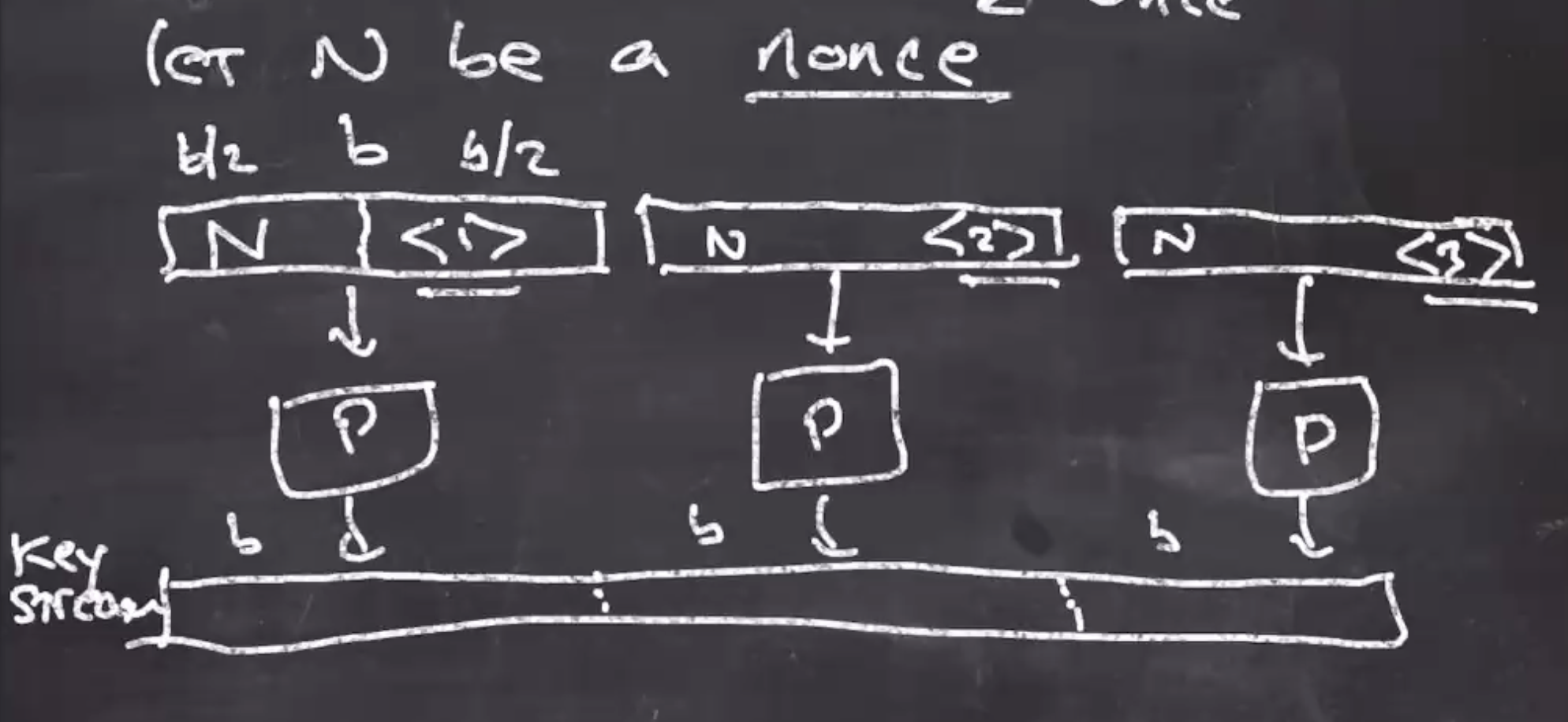The distribution of the key stream is very close to uniform.
• We then take our plaintext \( X \) and xor it with the key stream, \[\begin{aligned} Y = X \oplus \text{ key stream} \end{aligned}\]
• The nonce and the ciphertext are sent to the recipient
• This is now the most popular mode
• The counter should be incremented in an endian-neutral manner

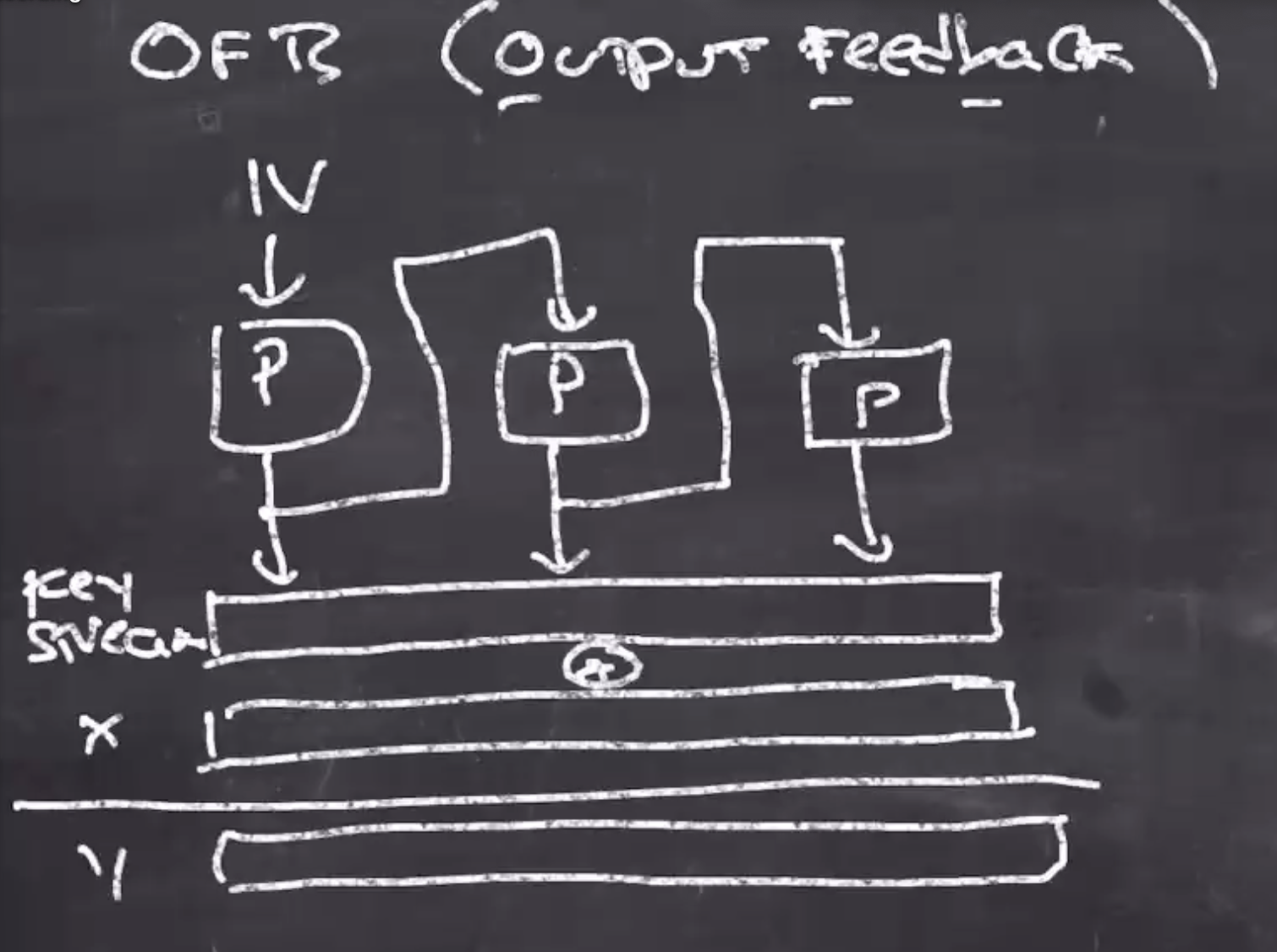
OFB (output feedback)

• Each output from \( P \) is fed into the next input for each block, and this creates a key stream
• We send \( IV \) and the ciphertext \( Y \)

Note: Our next programming assignment will be to implement the block cipher perm384bc and use the CTR mode to encrypt.

multiple messages in a row, diff nonce, same key for perm384bc?

Security model for encryption #

Cryptographers often come up with models that quantify how secure something is.

Real encryption should be indistinguishable from random. If the adversary cannot distinguish a ciphertext from random, then we consider that secure.

We can quantify this using distinguishing games, consider

• Real world
  • Init of black box: let \( k \) be a random key
  • on \( f(x) \) encrypt \( x \) with \( k \)
• Random world
  • Init of black box: let \( k \) be a random key
  • on \( f(x) \) encrypt \( x \) with \( k \) , then send back same number of random bits

If the distinguisher can’t tell the difference between these 2 worlds (ie the advantage is close to 0), then the encryption is good. Note that the adversary has an easy goal, just distinguish if its random or not. They don’t have to attempt to recover the plaintext, not even the key.

This is called “real or random” security.

Distinguishing algorithm for ECB mode #

• Real world
  • \( k \) is random
  • on \( x \) : ECB encrypt \( x \)
• Random world
  • \( k \) is random
  • on \( x \) : ECB encrypt \( x \) , then send back random bits of same length as ciphertext

Distinguisher:

x = <0>_b || <0>_b  // 2 of the same blocks
y = f(x)
y1 || y2 = y        // split y into 2 halfs
if y1 == y2:
    output "real"
else:
    output "random"

Therefore, by itself ECB is not secure.

Distinguishing algorithm for CTR mode #

• Real world
  • \( x,n \) is passed and the CTR encrypted ciphertext is returned
• Random world
  • Random bits returned (the same length as real world)

If we press the box \( q \) times:

for i from 1 to q:
    y[i] = f(<0>_b, <i>_b/2)
if any y[1]..y[q] are the same:
    output "rand"
else:
    output "real"

This is a good advantage if \( q \) is small and \( b \) is large.

Note: In AES, \(b = 128\).

Bounds in security #

In upper bound security: the adversary can’t do better.

• Essentially a proof that the adversary can’t do better.
• Harder to prove!

In lower bound security: the adversary does at least this well.

• An attack that proves you can do at least this well.

Security reduction #

A distinguisher box with either a random function or a block cipher with a random key:

block_cipher_distinguisher(g):
    f = CTR(g)              // let f be a CTR mode algorithm
    ans = real_or_random(f) // a function that tells what world we're in
    if ans == real
        output "block cipher"
    else:
        output "random"

This is a security reduction. It shows how you could break 1 thing, if you had another function to break it (real_or_random).

This establishes a upper bound of around the birthday bound as well. So since the upper and lower are almost the same, then they can make the claim of the actual security.

Galois Fields #

A Galois Field, usually denoted as \( GF(2^n) \) where its elements are \( n \) -bit strings.

So in \( GF(2^5) = \{00000, \ldots, 11111\}\) , where each of these elements represents a polynomial. So,

In order to call this a field, we have to define

• addition: add polynomials and mod coefficients by 2, ie \[\begin{aligned} 10101 + 11011 &= (x^4 + x^2 + x^0) + (x^4 + x^3 + x^1 + x^0) \\ &= 2x^4 + x^3 + x^2 + x^1 + 2x^0 \\ &\,\text{mod coeffecients by 2} \\ &= x^3 + x^2 + x^1 \\ &= 01110 \end{aligned}\] Note that this entire process is simply the xor of the 2 inputs! \[\begin{aligned} 10101 \oplus 11011 &= 01110 \end{aligned}\]

• multiplication: multiply the polynomials, mod by modulus, mod coefficients by 2 \[\begin{aligned} 10101 + 11011 &= (x^4 + x^2 + x^0)(x^4 + x^3 + x^1 + x^0) \\ &= x^8 + x^7 + x^6 + 2x^5 + 2x^4 + 2x^3 + x^2 + x^1 + x^0 \\ &\text{ mod coeffecients by 2} \\ &= x^8 + x^7 + x^6 + x^2 + x^1 + x^0 \\ &\text{ mod by irreducible polynomial} \\ &= x^8 + x^7 + x^6 + x^2 + x^1 + x^0 \mod x^5 + x^2 + x^0 \\ &= x^4 + x^2 \\ &= 10100 \end{aligned}\]

  Polynomial modulus work

  

  Note: We use the irreducible polynomial: \( x^5 + x^2 + x^0 \) to mod by. This came from a lookup table for \(GF(2^5)\).