Bitwise manipulations #
File: Slides

Data is a sequence of bytes in memory, whether we receive it from a file or network. We will use unsigned int types to avoid sign extension. These manipulations are powerful in cryptography.

We can also move the bits back and forth using left/right shifts. Bits that shift off the end are gone for good, and 0s are added on the opposite end (in unsigned types).
Common uses #


Correction: we are clearing bit position 7 in the above slide.
x = x & ~(1 << 7);

Correction: above slide should shift right 7.
x = 1 & (x >> 7);

Rotations are very common in encryption.

Here, (x & 0x000000FF) is called a mask.
It masks everything except the last 8 bits.

On Intel CPUs, the return value is left in %eax.
Array allocation #
File: Slides

Auto allocated memory only exists in scope, you can’t have long lived memory this way.

Remember, malloc takes the number of bytes you want, not the number of elements.
If malloc is unsuccessful, it will return 0 (NULL).

Reverse array example #

This could crash if you have less than 400B on the stack available.

This uses \( O(n) \) space complexity.

Obtaining memory addresses #

Inverse techniques in C #
AXR – add, XOR, rotate #
We can write an invertible functions using these 3 operations.
- add
- xor
- rotation
Consider something like
x = x + y;
This can be “undone” via
x = x - y;
These work with the other operations, i.e.
x = x ^ y;
x = x ^ y; // xor is its own inverse
Note: XOR is associative:
(x ^ y) ^ y = x ^ (y ^ y)
Rotation (we’ll use <<< to indicate left rotate):
x = x <<< y;
x = x >>> y; // or x = x <<< (32 - y)
Note: You can either rotate back, or continue to rotate the entire width.
Here we are assuming that x is a 32 bit value
We can compose these 3 operators to scramble bits (and is invertible):
uint32_t scramble(uint32_t x)
{
x = x ^ 0x1AFE9B3A; // xor by random constant
x = x << 12;
x = x + 0x2783AFBC; // add random constant
return x;
}
We could easily write the invertible function to undo these operations:
uint32_t unscramble(uint32_t x)
{
x = x - 0x2783AFBC; // sub random constant
x = x >> 12;
x = x ^ 0x1AFE9B3A; // xor by random constant
return x;
}
The operations just have to happen in the opposite order of scramble.
Feistel #
Another way to write an invertible function in C is to use a Feistel construction. The idea is that the construction itself is invertible, and not the components.
We can take an input and break it into 2 pieces, and use one half to cause a scrambling of the other half.
An abstract example in C, (here f doesn’t exist).
// x points to an array of two uint32_t
void fscramble(uint32_t * x)
{
x[0] = x[0] ^ f(x[1]) // f returns random looking uint32_t
x[1] = x[1] ^ f(x[0]) // f returns random looking uint32_t
}
Note: Here, f is some kind of scrambling function.
To undo these operations, we just need to do the original operations in reverse order:
// x points to an array of two uint32_t
void funscramble(uint32_t * x)
{
x[1] = x[1] ^ f(x[0]) // f returns random looking uint32_t
x[0] = x[0] ^ f(x[1]) // f returns random looking uint32_t
}
What is interesting about these Feistel structures, is that f itself does NOT need to be invertible.
A concrete example:
// x points to an array of two uint32_t
void fscramble(uint32_t * x)
{
x[0] = x[0] ^ (x[1] * x[1] + x[1]) // square and add
x[1] = x[1] ^ (x[0] * x[0] + x[0]) // square and add
}
// x points to an array of two uint32_t
void funscramble(uint32_t * x)
{
x[1] = x[1] ^ (x[0] * x[0] + x[0]) // square and add
x[0] = x[0] ^ (x[1] * x[1] + x[1]) // square and add
}
Composing simple ciphers #
We will make a simple function that is invertible, but simple to create. Historically, cryptography uses permutations the most for ciphers.
Caesar cipher #
One of the oldest uses of cryptography was used in Roman times, the Caesar cipher. They selected a number to be used as a fixed key. So long as the key wasn’t leaked, it provided adequate privacy.
It is a simple shift of the alphabet, so \( A \to D, B \to E \) , etc. At the end you wrap around, \( Z \to C \) .
So if we are encrypting the word BAD, and are shifting by 3:
B A D
E D G add 3
B A D sub 3 to get original
This is known as a shift cipher.
shift(x):
ciphertext = x + 3 mod 26
We can make this more flexible and more secure by using the key and the character:
shift(x, k):
ciphertext = x + k mod 26
So we can get the plaintext by doing the opposite:
plaintext = y - k mod 26
// or
= y + (26 - k) mod 26
This is working in the field
\( Z_{26} \)
, meaning we use mod 26.
The goal of this is to have the ciphertext and the function to look very random.
So if we encrypt using a key of k, and are in the field
\( Z_5 \)
.
k = 3
encrypt(k, x) = x + k mod 5
This is a permutation function, and all it does is add 3 to each of its inputs.

This doesn’t “look random”, as it seems that all of the arrows are parallel.
However, it is secure as long as k is picked at random, and we only encrypt a single x.
Each of the outputs are equally likely, therefore the ciphertext is secure.
Normally however, we don’t usually encrypt a single character. We want our permutation that we are going to use to be more random so we can encrypt more than 1 char at a time.
Multiplicative cipher #
Here instead of using addition (like the shift cipher), we will use multiplication.
So if we are in \( Z_{26} \) .
\[\begin{aligned} e(k,x) &= xk \mod 26 \\ d(k,y) &= y k^{-1} \mod 26 \end{aligned}\]This only works if the multiplicative inverse \( k^{-1} \) exists in \( Z_{26} \) . The inverse of \( k \) has to be an element in \( Z_{26} \) , normally people think of fractions as inverses.
Note that not all values in \( Z_{26} \) have an inverse.
\( k^{-1} \) exists iff \( gcd(k,26) = 1 \) .
If \( k \) and \( 26 \) share no factors, then it has a multiplicative inverse.
The easiest way to find candidates for \( k \) is:
- Go through all of the numbers in \( Z_{26} \) and throw out the prime factors that have 26.
So 26 has two prime factors: \( 26 = 2 * 13 \) .
So we throw out all the ones that have a multiple of 2 or 13, whats left is the numbers that have a multiplicative inverse, i.e.
\[ k = 1,3,5,7,9,11,15,17,19,21 \]So lets see how random the multiplicative cipher looks compared to the shift cipher:
If \( k = 3 \) and \( Z_5 \to Z_5 \) :
\( E(k,x) = kx \mod 5 \)x |
E(3,x) |
|---|---|
| 0 | 0 |
| 1 | 3 |
| 2 | 1 |
| 3 | 4 |
| 4 | 2 |

This looks a lot more random than the shift cipher. However, it looks like 0 will always map to 0 in a multiplicative cipher. Also, even though the arrows aren’t parallel, they still have some regularity to them. So we can do better.
Composing ciphers #
Principle: Composing simple ciphers of different structures yields a more random looking cipher.
If we compose 2 invertible functions, the composition will still be invertible.
For example, if we start with a shift cipher, and then use a multiplicative cipher:
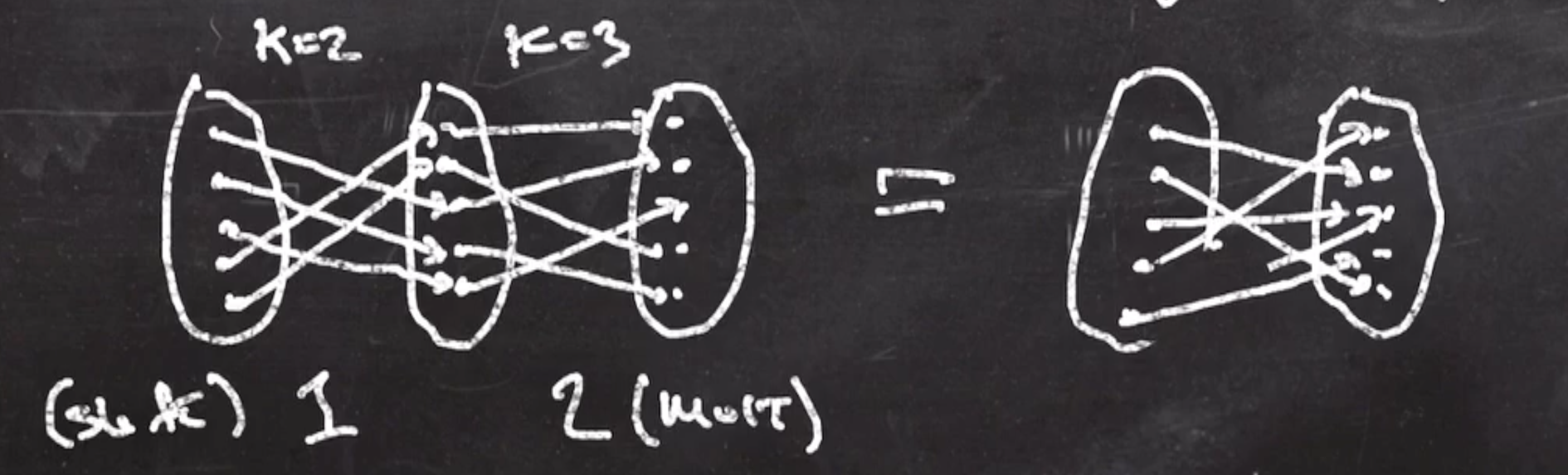
Correction: On right, 2 goes to 2, and 4 goes to 3.
You need to alternate between different ciphers to add security. (Composing 2 shifts wouldn’t add any additional security than 1).
Example of a non-linear simple cipher #
An example of a non-linear cipher is a transposition cipher.
It considers the data to be in chunks, it doesn’t scramble the characters, but rearranges them:

It is a simple cipher (because it is reversible), and it is a permutation (domain and codomain are same). It is non-linear because it cannot be represented by the sum of product terms.
Connection to AXR operations:
- add is a shift cipher in \( Z_{2^n} \)
- xor is a shift cipher in \( Z_2 \), for example \(a \oplus b = a + b \mod 2\)
- rotate is a transposition.
We usually don’t use multiplication because it is more computationally expensive.