More reduction examples #
The SAT problem #
One of the first problems to be proved NP-Complete.

Both parts highlighted in red must be true. It is easy to make the right side false by setting \( x_2 \) to false.

Note that the red circled part cannot be true, and since it is being OR’d we need to make sure that the left side is true.


So, it is satisfiable.
\( \to \) means "if"\( \leftrightarrow \) means “if and only if”

Conjunctive normal form #

- if each clause has 3 literals, we call it 3CNF
- similarly for 4

Consider a 1CNF:
\[\begin{aligned} x_1 \wedge x_2 \wedge \bar{x_1} \end{aligned}\]We can find out if this is satisfiable or not by trying to make each clause true. Note that \( x_1 \) creates a contradiction. So, 1CNF expressions are not NP-Complete. Similarly for 2CNF.

- while we don’t show the proof here, we can now use the fact that 3CNF is NP-Complete to prove other problems are NP-Complete (by reducing 3CNF to the other problems).
The clique problem #



Lets reduce this instance of a 3CNF problem to an instance of a \( k \) -clique problem:
We can split each clause up into a group of 3 vertices. Connect vertices if they are the same boolean value in all clauses.
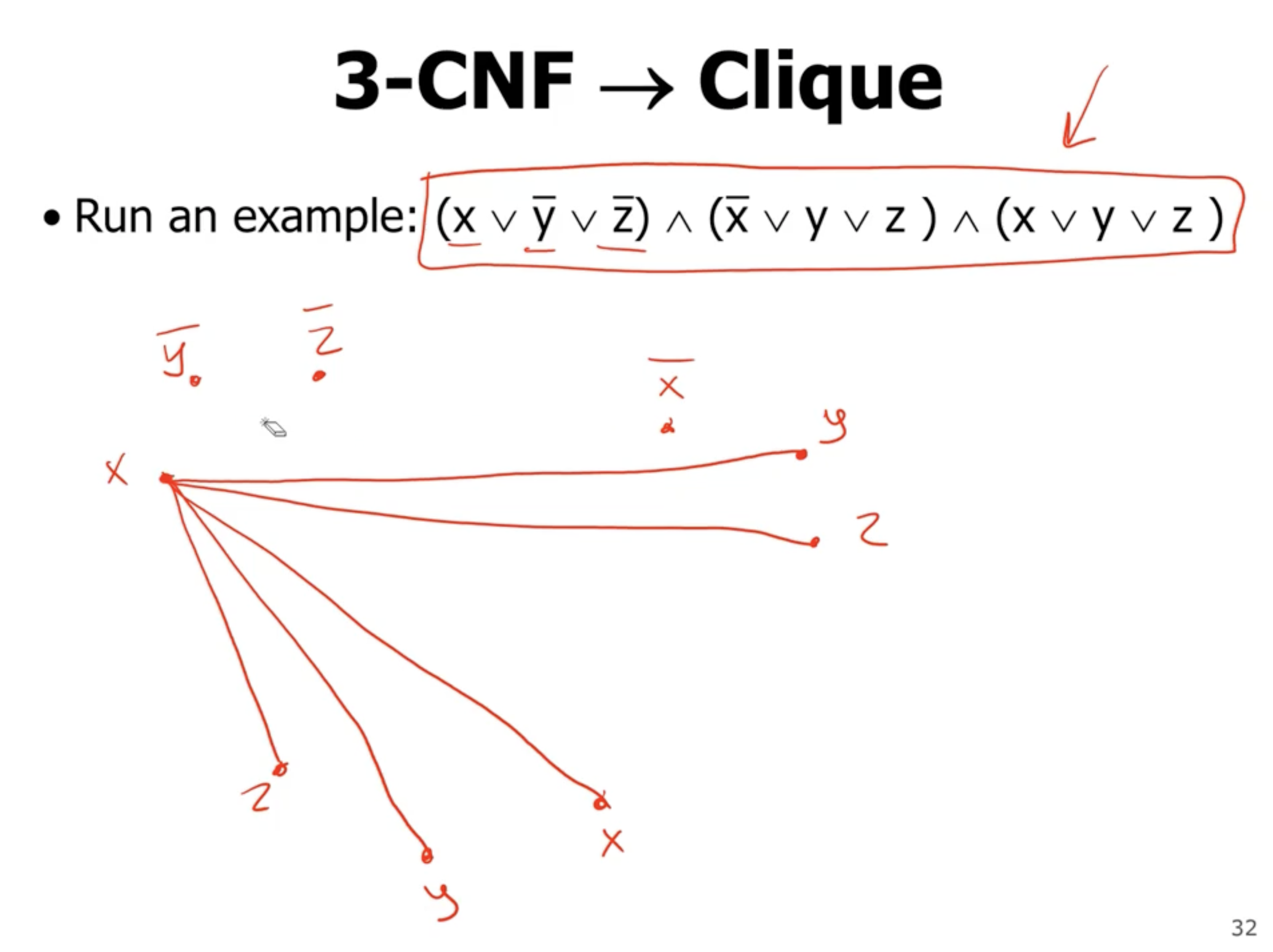



So how do we prove that this is a valid reduction?
- the creation of this graph was done in polynomial time
- we need to prove that the answer to the 2 problems are the same
- if the 3CNF is satisfiable, then at least 1 literal from the clauses is true, which means we would have a \( k \) -clique in the graph
- if we have a \( k \) -clique in the graph, then the 3 vertices of the clique will be from 3 different clauses, and therefore the 3CNF will be satisfiable
Reducing the clique problem to the vertex cover problem #
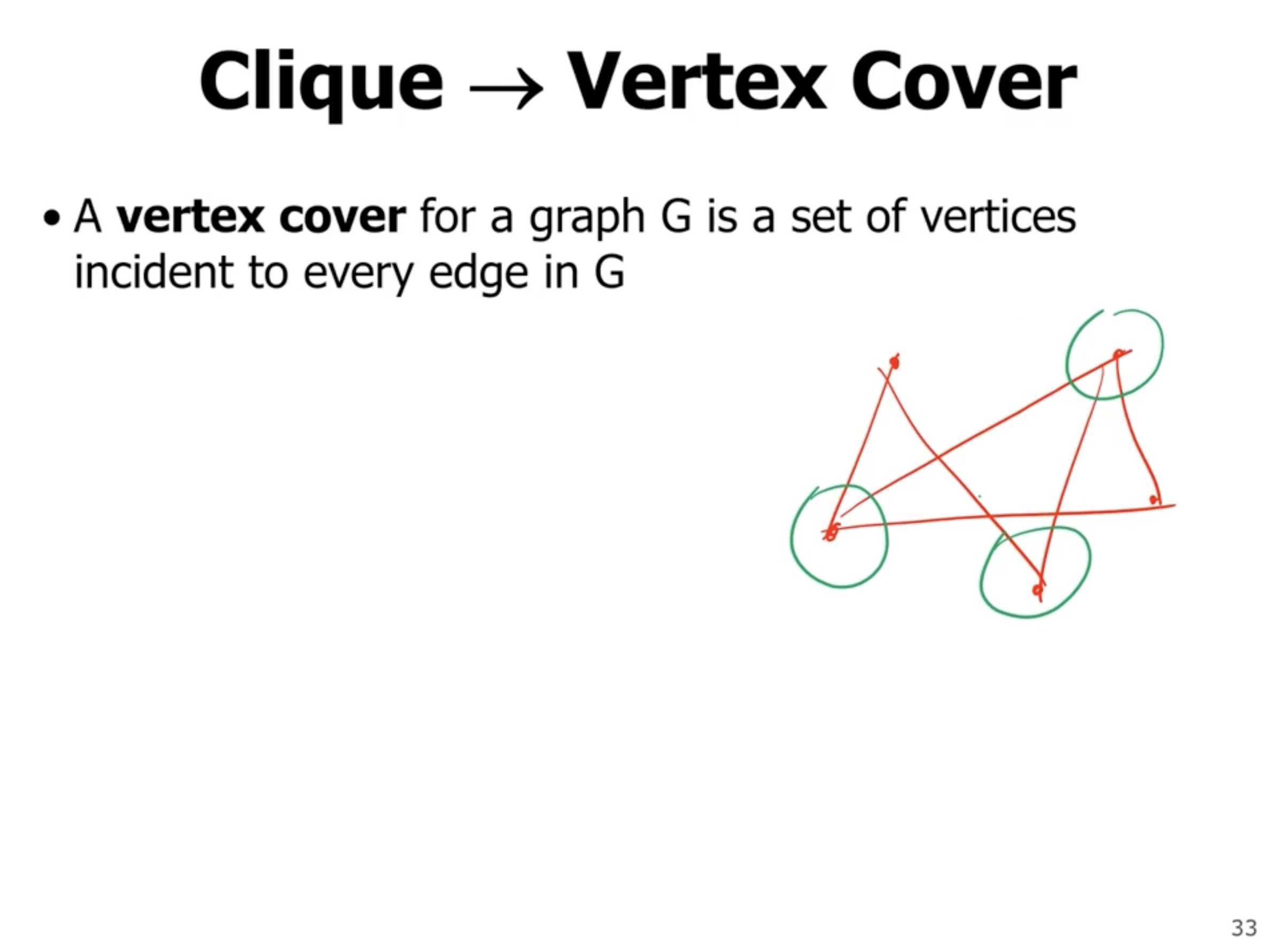
Each edge has an endpoint in one of the 3 circled green vertices.
We can check if it has a 1 vertex cover, if no then we can increase the question. If the graph has 2 vertex cover, then the minimum number is 2 for vertex cover. At most, we can have \( n \) vertex cover.
So how can we reduce the clique problem to the vertex cover problem?




- the complement of a clique has no edges
- so, any other edge in the graph can be covered by the other vertices not among the clique (there are \( n - k \) of them).


General reduction comments #

