Quicksort #

The way that the array is divided matters.

Partitioning the array using Hoare’s partition #

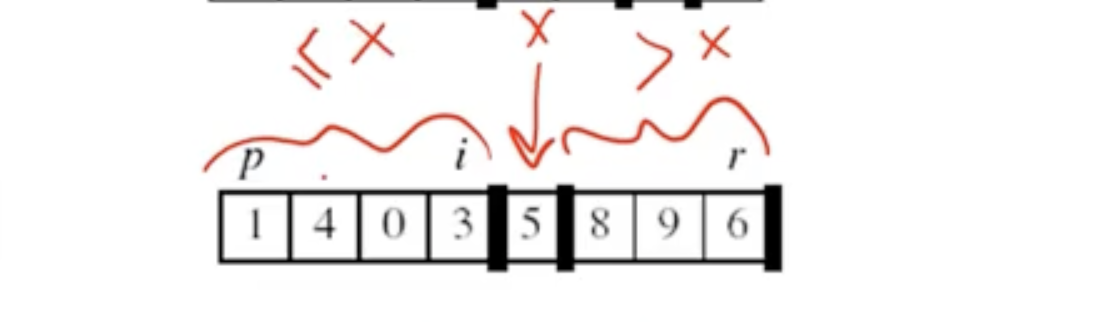
i will move toward the right until it reaches a element that is bigger or equal to the pivot point. j will move to the right until it finds a element that is less thatn or equal to the pivot point. i and j will swap as long as the pointers haven’t crossed paths.

When i and j cross each other, then the 2 subarrays are partially sorted.

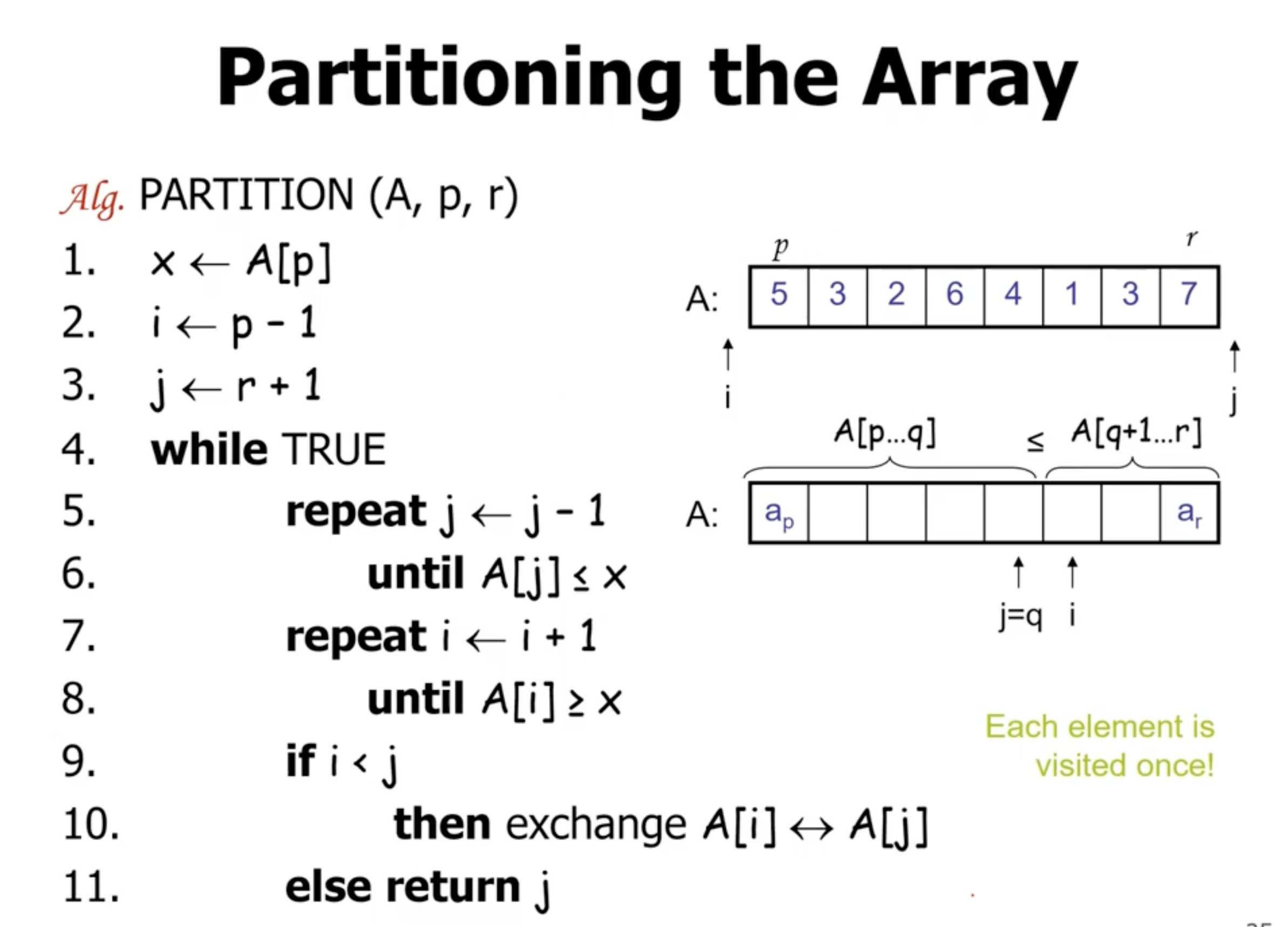
The runtime for partition is \( \Theta (n) \) .

Quicksort algorithm #

We don’t actually have to explicitly combine the 2 arrays, because they are next to each other and they will be already sorted.

So the runtime for quicksort in general is \[\begin{aligned} T(n) &= T(q) + T(n-q) + f(n) \end{aligned}\]

where \( f(n) \) depends on the partition function. However, we can’t be fully sure that the time complexity given the input (the value of \( q \) ). If partition divides the 2 subarrays into size 1 and everything else, then the worst case complexity happens. So, quicksort is really bad at sorting arrays that are already in order (or close to it).

Lomuto’s partition method #

• The pivot is the last element in the array.
• i starts pointing to the blank space before the array.
• j moves to the right until it sees an element that is less than or equal to x.
• i then moves one to the right, and the pointers swap.

Once j reaches the pivot, the pivot is swapped into the element to the right of i.

The good thing about this approach is we don’t need to contain the pivot element in the recursive call. So we remove at least 1 from the total size of the sub problems.

Note: The pivot point is not included in the subarrays.

Randomizing quicksort #

Quicksort performs at its worst when the array is already sorted (or close to it).

The pivot element can be chosen randomly, then swapped into either the first or the last element of the array, depending on which partition algorithm we’re using.

Example problems #

This can be solved naievly like so

for i from 0 to n-1
    for j from 1 to n
        compare a[i] and a[j]

But this results in a \( \Theta(n^2) \) time complexity. So the solution is to sort the array first, then we can check adjacent pairs.

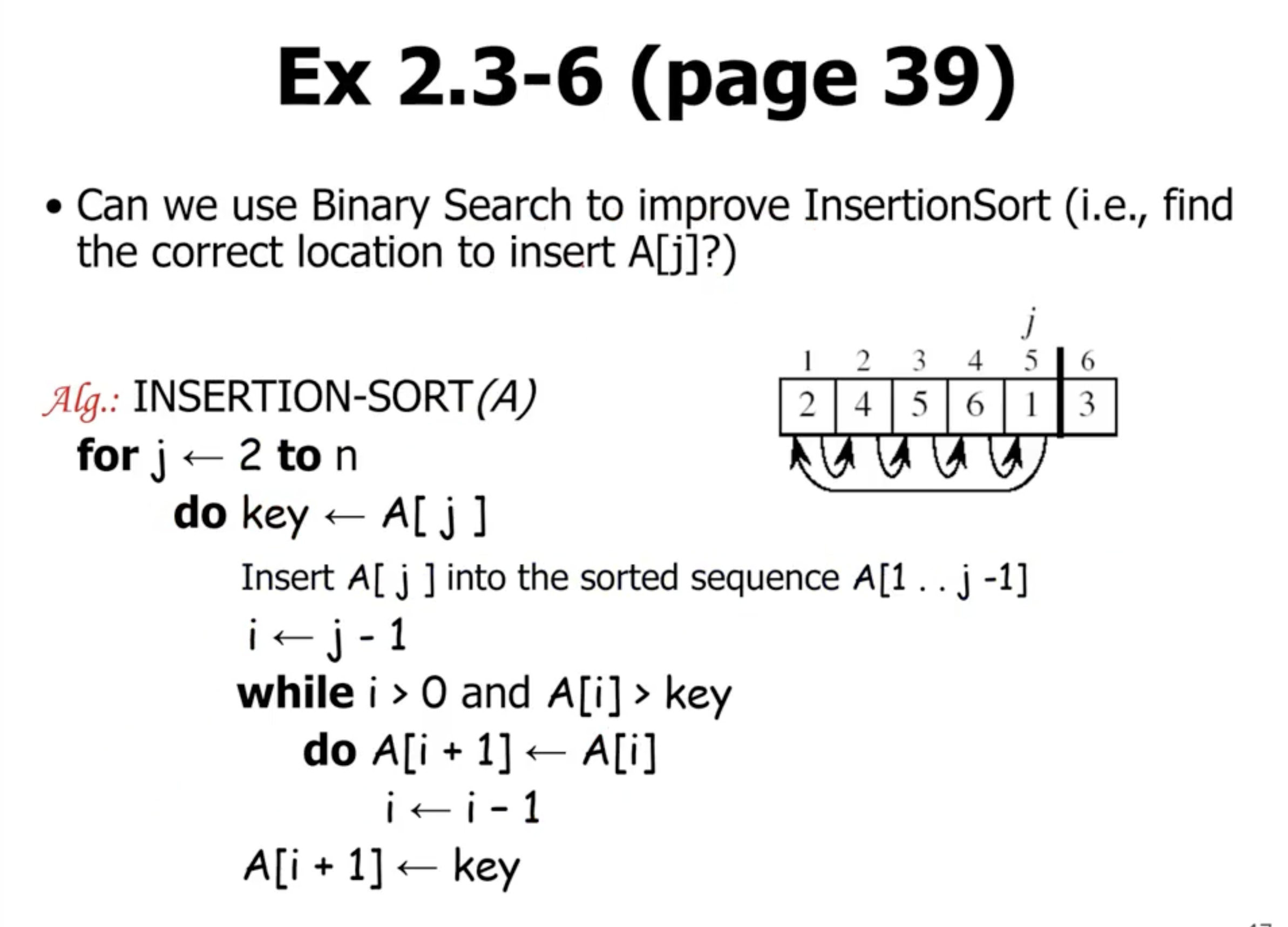
While we could use a binary search on the already sorted subarray, we would need to shift all the elements down to insert the new element into place.

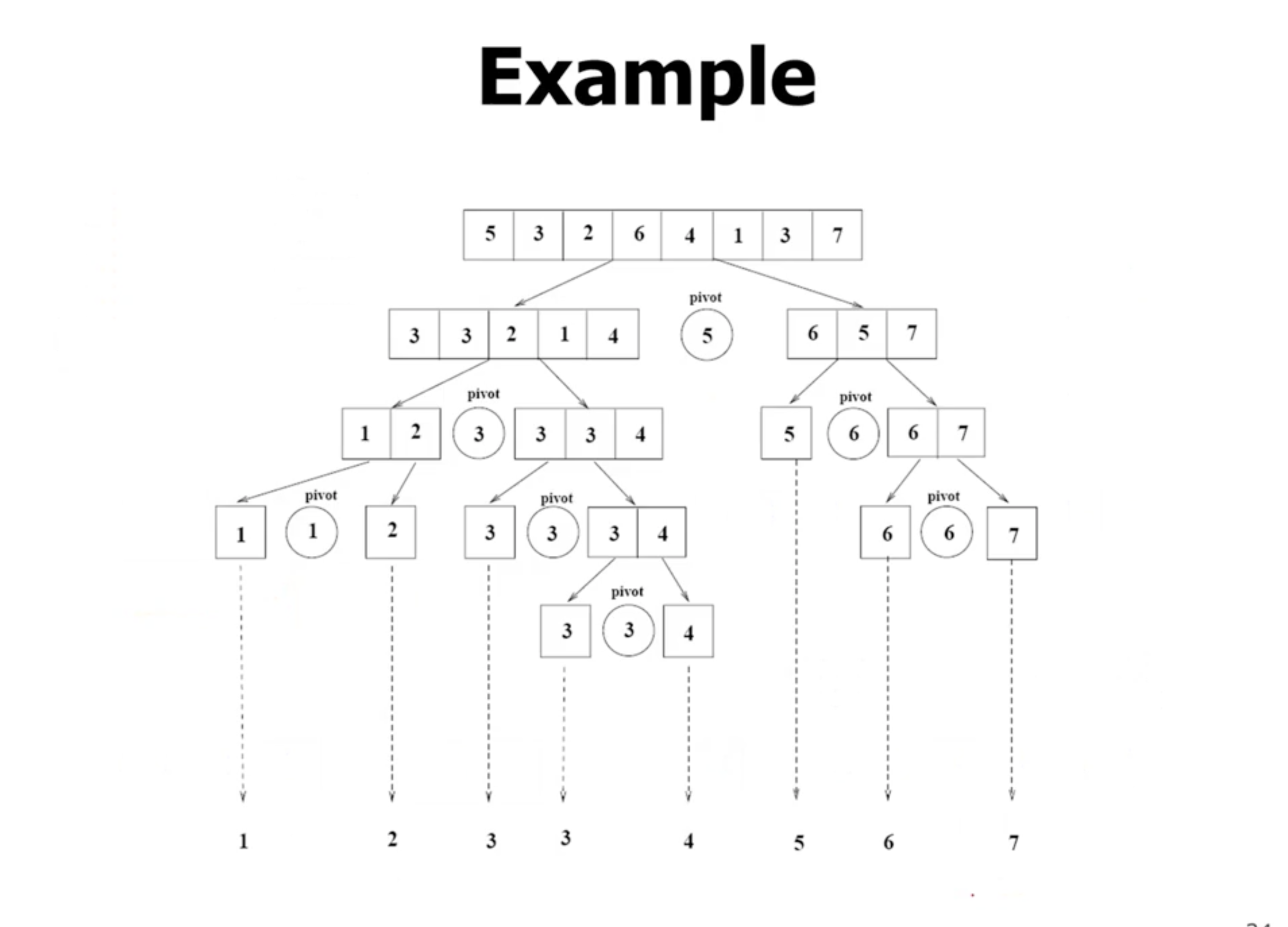
In this case, where all elements are the same, i and j will instantly stop and swap. So each element will actually have to be swapped. Once the pointers pass each other, then each sub array will also have to “sort”. So, the overall time complexity when quicksorting an array of identical elements using Hoare’s partition is \( \Theta(n \lg n) \) .

When using Lomuto’s partition, the element will swap with itself. The index returned will be the last element, and then the subarrays will be of great unequal size. So quicksort using this partition method will give a time complexity of \( \Theta(n^2) \) .