Divide and conquer #

A problem divided into any ratio, with the rest of the problem a complement of the original input, the overall complexity will still be \( \Theta(n \lg n) \) .

Mergesort #

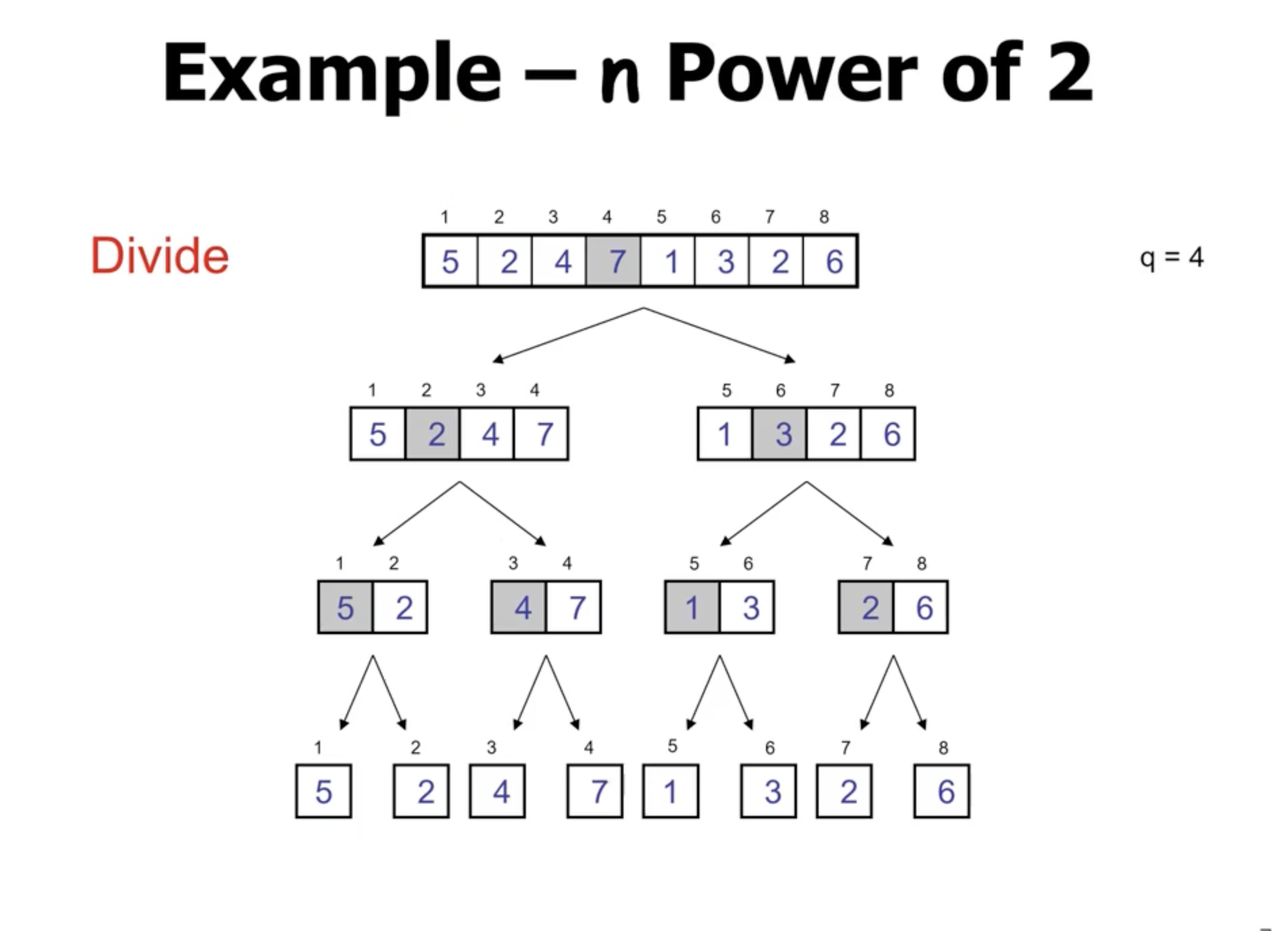
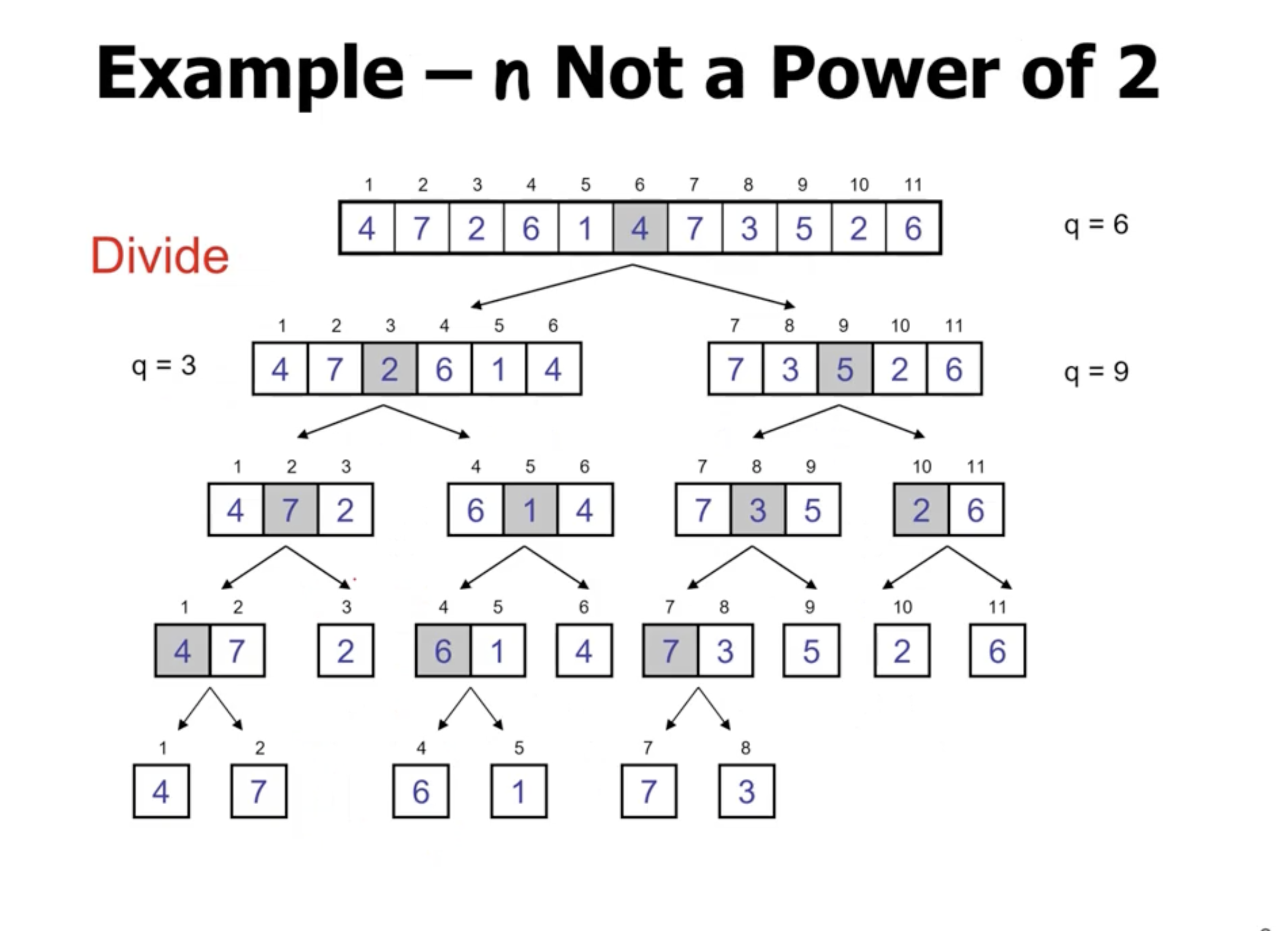
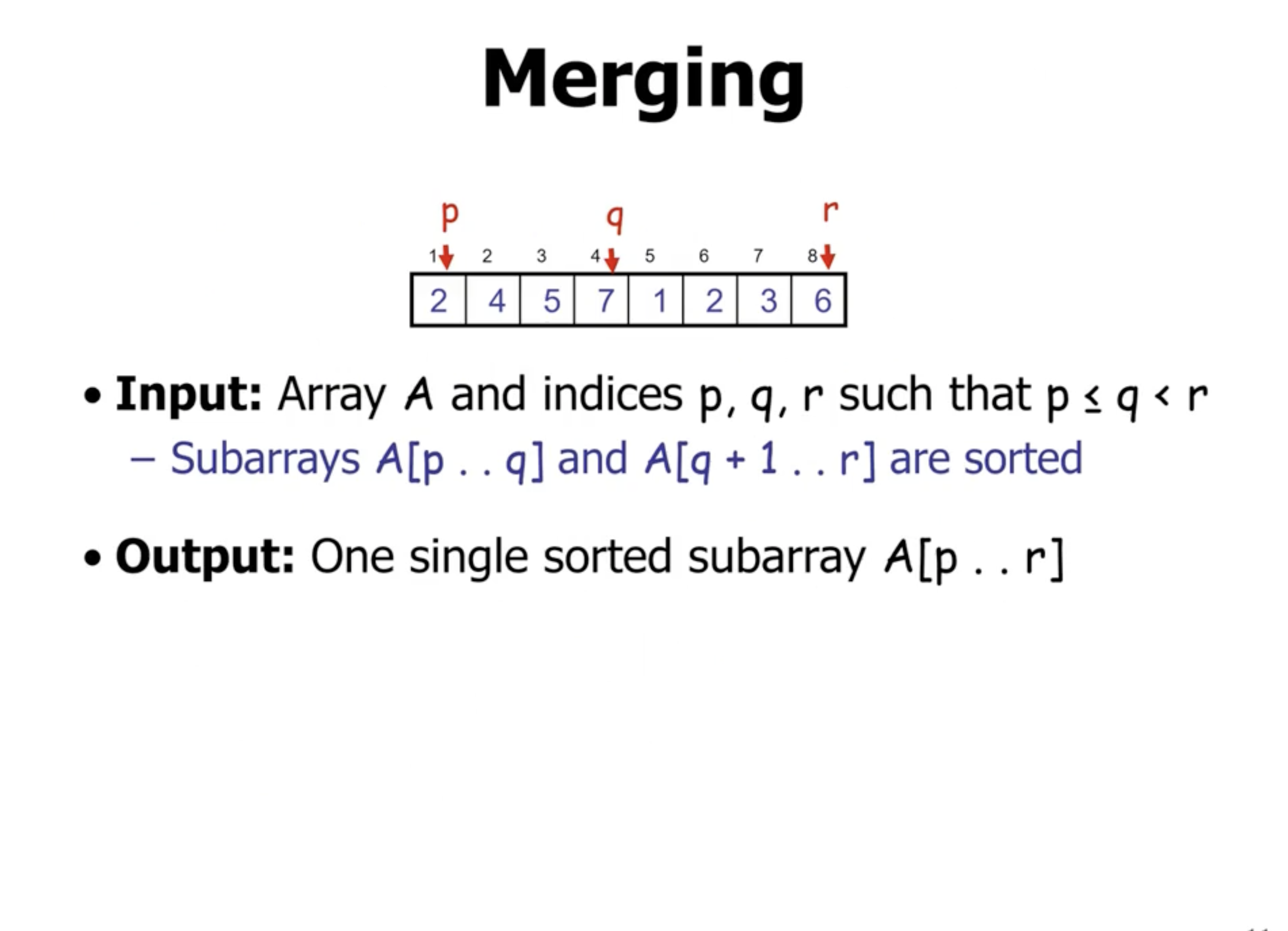
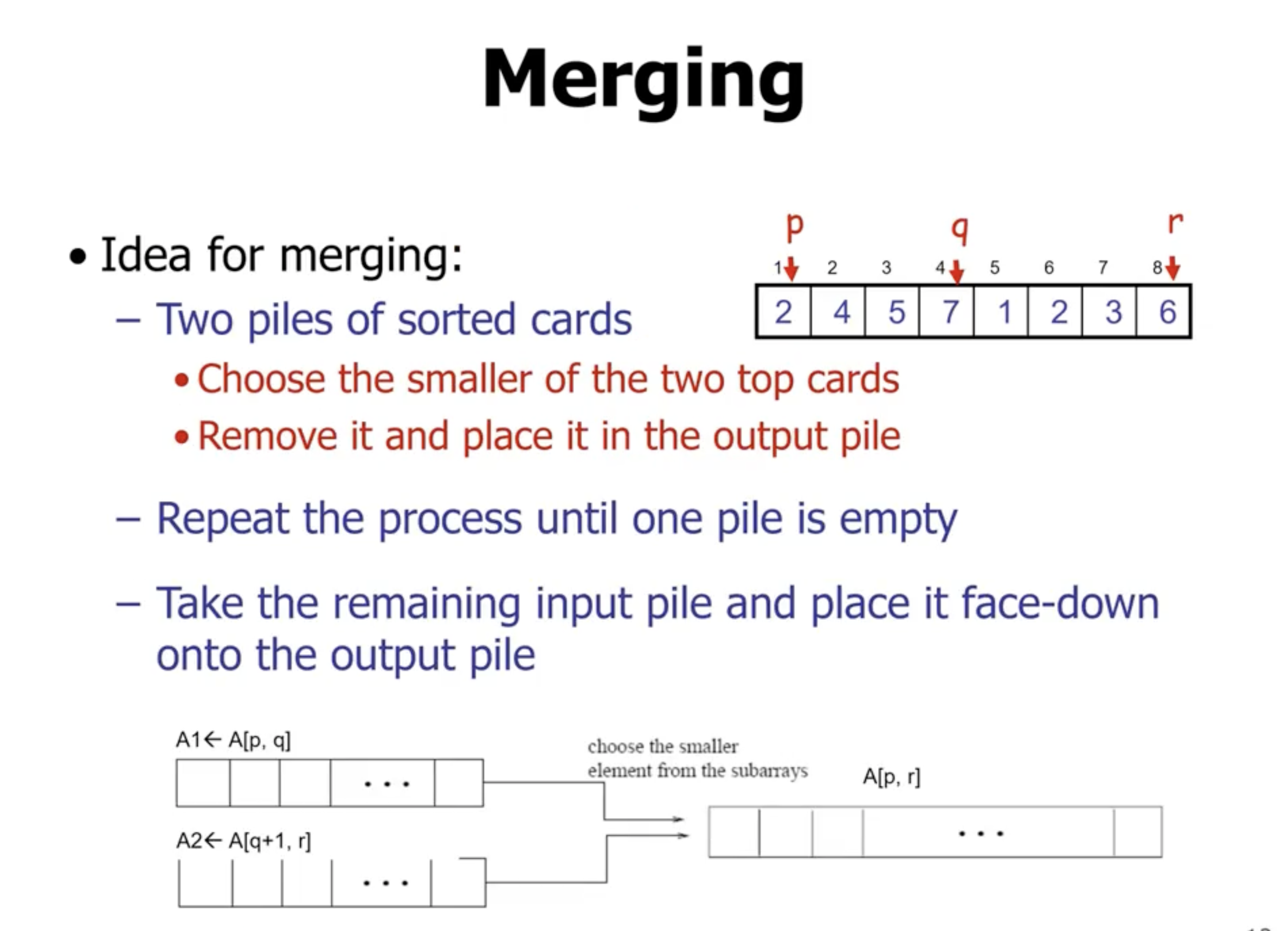
Mergesort does not sort in place. During merge, it copies each subarray to a new array, then places them back into the original.

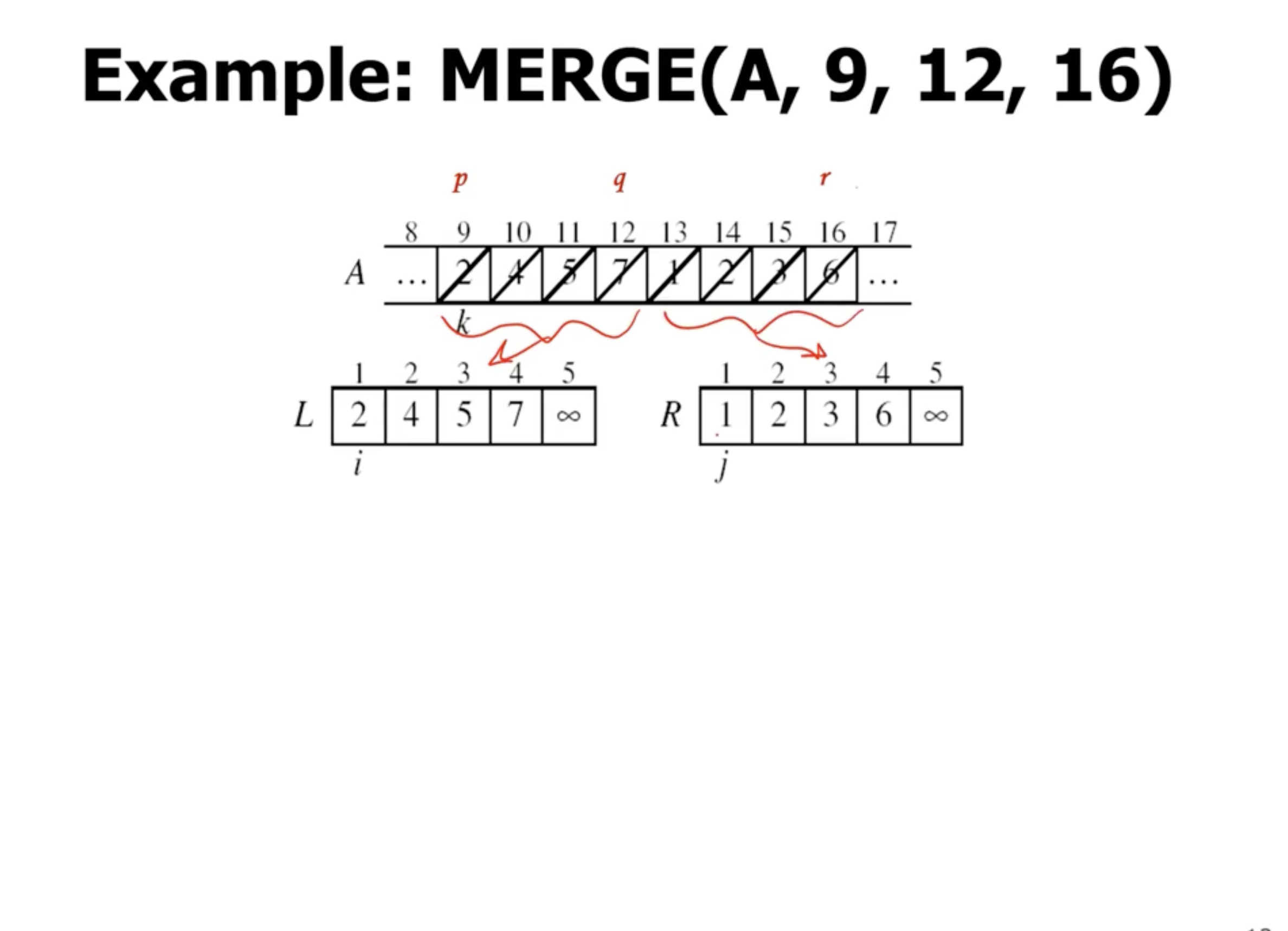
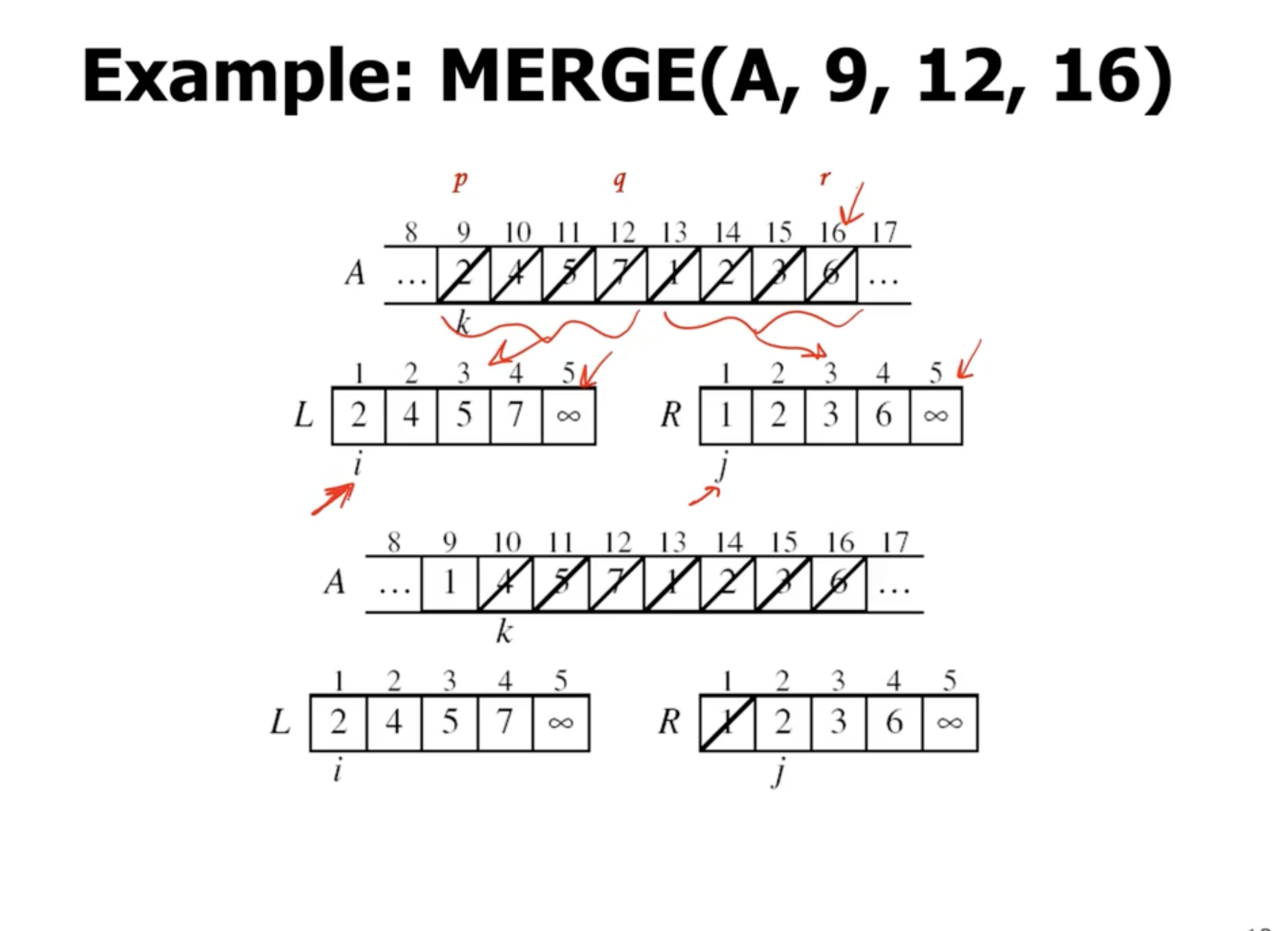
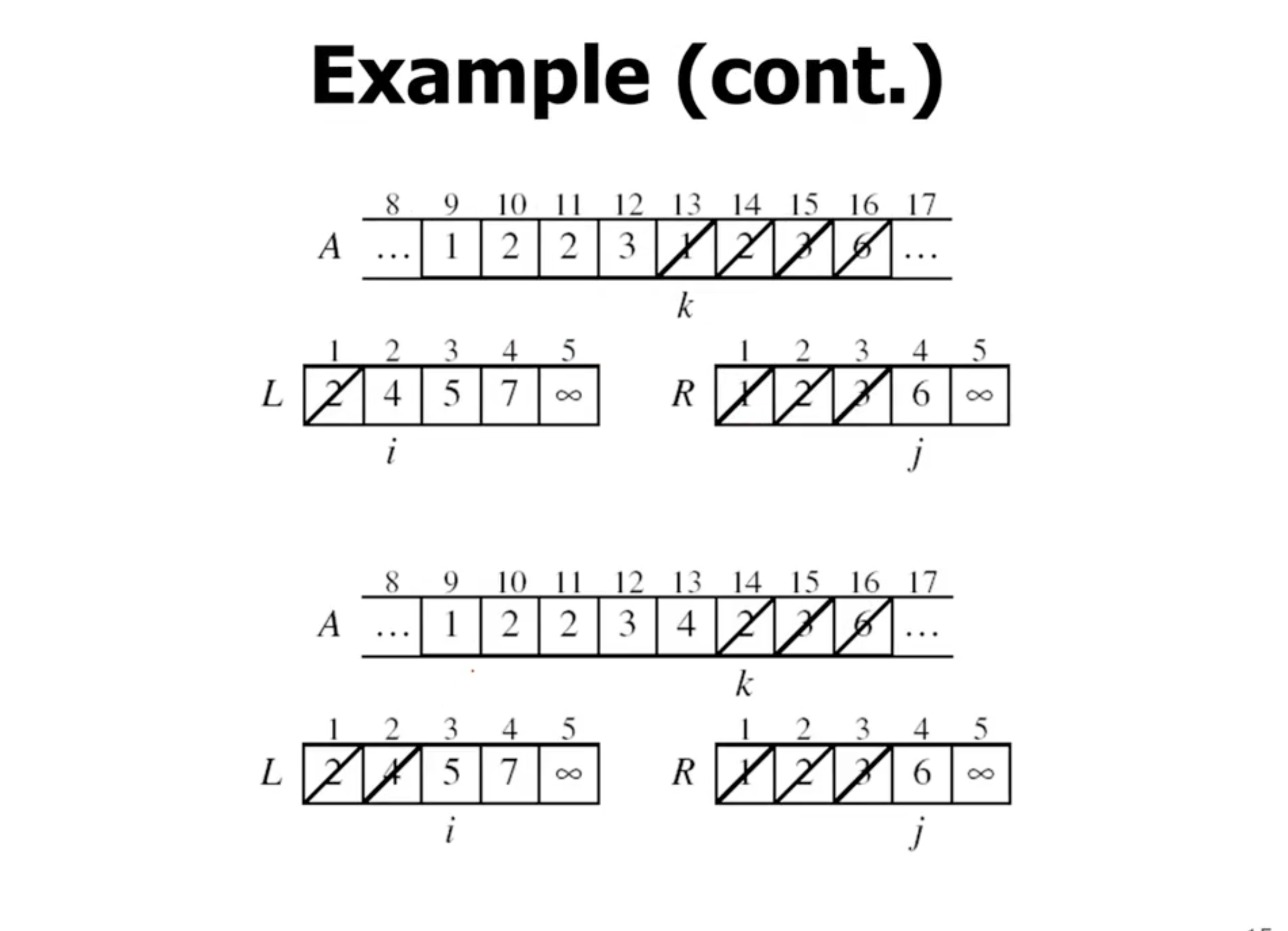
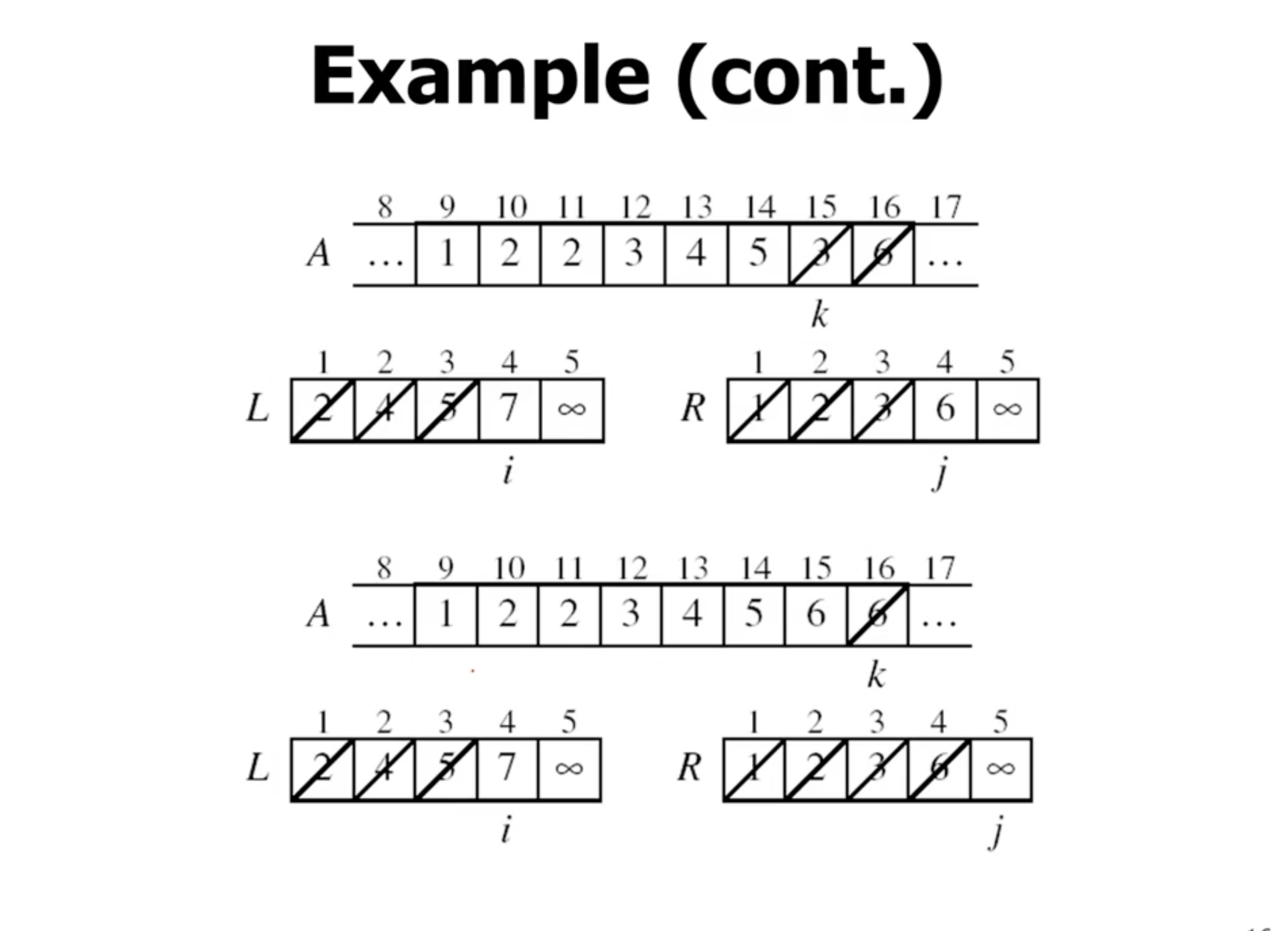
Merge function #

Analyzing divide and conquer algorithms #

Advantages and disadvantages #

Sorting challenges #

The sorting problem is generally sorting the keys of records.

While some algorithms time complexity, like selection/bubble/insertion, may have a runtime complexity of \( O(n^2) \) , the actual comparisons and swapping during the algorithm may happen more than that amount. However, since we are just comparing the keys, and not the huge records, we don’t have to take this into account.

This examples shows us that merely comparing the runtime complexity is not always the best way of comparing algorithms. For example, if we are swapping huge records, then the algorithm with the least amount of swaps will be best (even if it has a worse runtime complexity).

In this problem, since the number of elements is huge, we don’t want to choose the algorithm that has the last amount of swaps. The actual amount of comparisons will be a better way to choose our algorithm. In this case, we will choose mergesort.

If we have an array that is almost sorted, then insertion sort will do the best. Bubble sort will have to still do \( n^2 \) comparisons, even if only 1 element is out of order (the lowest at the end).