Backtracking #
Recursive programming can be divided into two categories. One category creates the solution, and the other searches for the solution.
When searching, we want to consider backtracking.



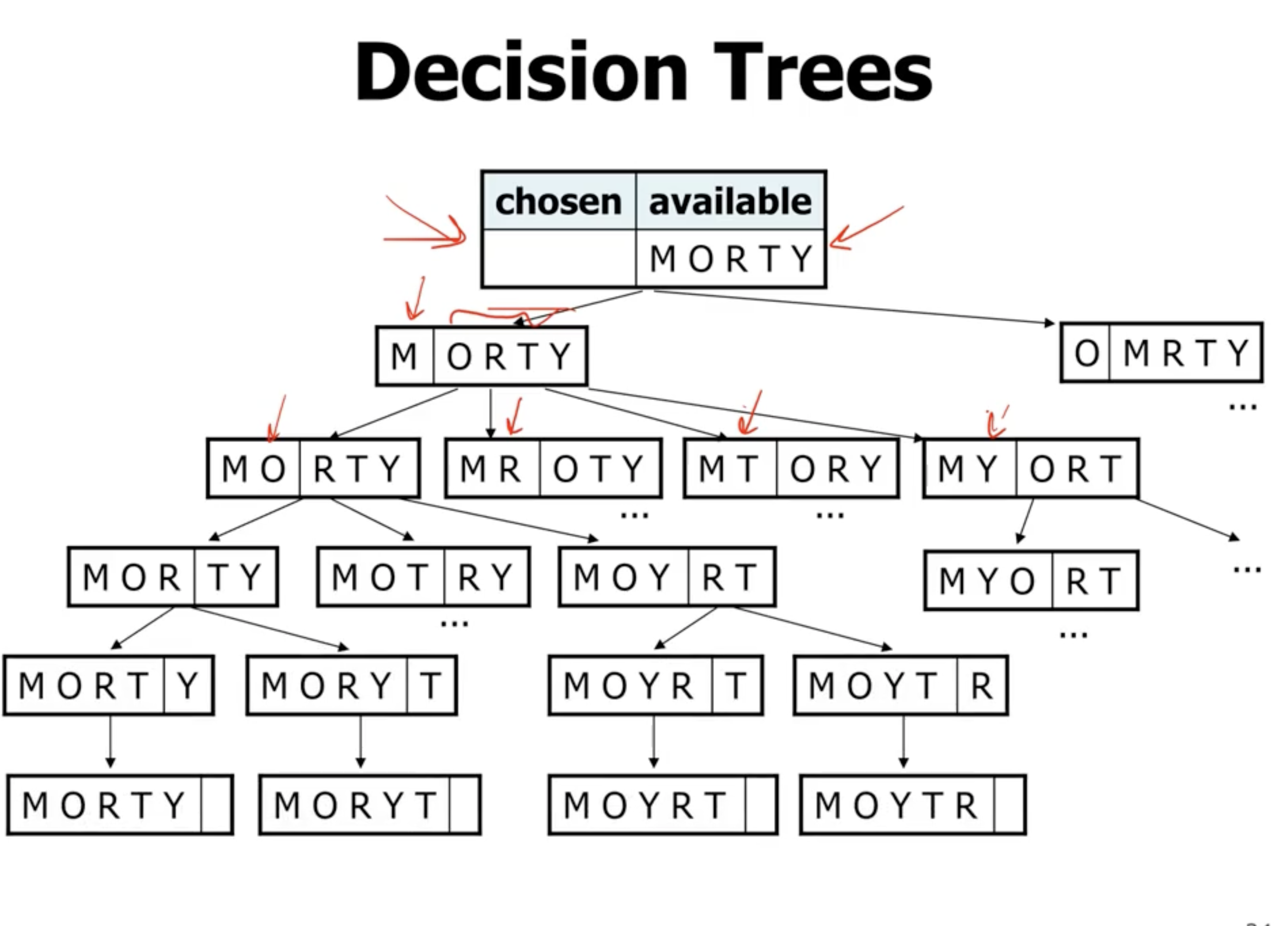
We can search these decision trees for our solution in the solution space. When looking for a solution, if we ever reach a subtree that doesn’t meet our criteria, we can backtrack.


Strategies #


Examples #

Pretend that our maze is represented with 0 and 1, a 2D array where 0 is a wall and 1 is not, something like this:

We can make a choice, and explore until the end, then backtrack to unchoose and make a new choice.
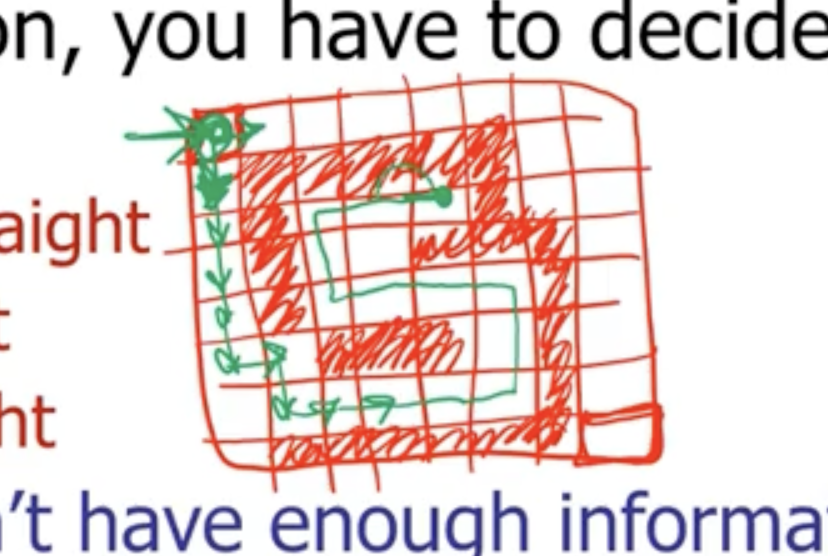
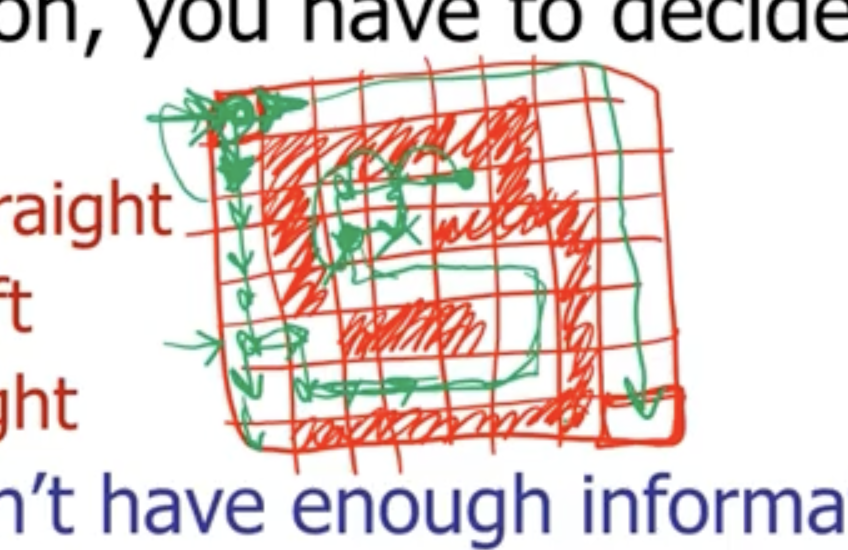






Note: Remember, the order doesn’t matter in a combination.
My solution in python
def permute(s):
""" outputs all possible rearrangements of letters in string s """
def _permute(s, chosen):
if len(s) == 0:
print(chosen)
else:
for i in range(len(s)):
_permute(s.replace(s[i], ""), chosen + s[i])
_permute(s, "")
def combinations(n, k):
""" outputs all k combinations of the first n positive integers """
nums = [i for i in range(1, n + 1)]
def _combinations(n, k, start, output):
if len(output) == k:
print(output)
else:
for i in range(start, len(nums)):
_combinations(n, k, i + 1, output + str(nums[i]))
_combinations(n, k, 0, "")
if __name__ == '__main__':
print('permute("morty")')
permute("morty")
print("combinations(6, 3)")
combinations(6, 3)
Output
permute("morty")
morty
moryt
motry
motyr
moyrt
moytr
mroty
mroyt
mrtoy
mrtyo
mryot
mryto
mtory
mtoyr
mtroy
mtryo
mtyor
mtyro
myort
myotr
myrot
myrto
mytor
mytro
omrty
omryt
omtry
omtyr
omyrt
omytr
ormty
ormyt
ortmy
ortym
orymt
orytm
otmry
otmyr
otrmy
otrym
otymr
otyrm
oymrt
oymtr
oyrmt
oyrtm
oytmr
oytrm
rmoty
rmoyt
rmtoy
rmtyo
rmyot
rmyto
romty
romyt
rotmy
rotym
roymt
roytm
rtmoy
rtmyo
rtomy
rtoym
rtymo
rtyom
rymot
rymto
ryomt
ryotm
rytmo
rytom
tmory
tmoyr
tmroy
tmryo
tmyor
tmyro
tomry
tomyr
tormy
torym
toymr
toyrm
trmoy
trmyo
tromy
troym
trymo
tryom
tymor
tymro
tyomr
tyorm
tyrmo
tyrom
ymort
ymotr
ymrot
ymrto
ymtor
ymtro
yomrt
yomtr
yormt
yortm
yotmr
yotrm
yrmot
yrmto
yromt
yrotm
yrtmo
yrtom
ytmor
ytmro
ytomr
ytorm
ytrmo
ytrom
combinations(6, 3)
123
124
125
126
134
135
136
145
146
156
234
235
236
245
246
256
345
346
356
456

8 queens problem #

Given an 8 x 8 chessboard, place 8 queens so they can not attack each other.
Note: This can be written for \( n \) queens in a \( n \times n \) chess board.
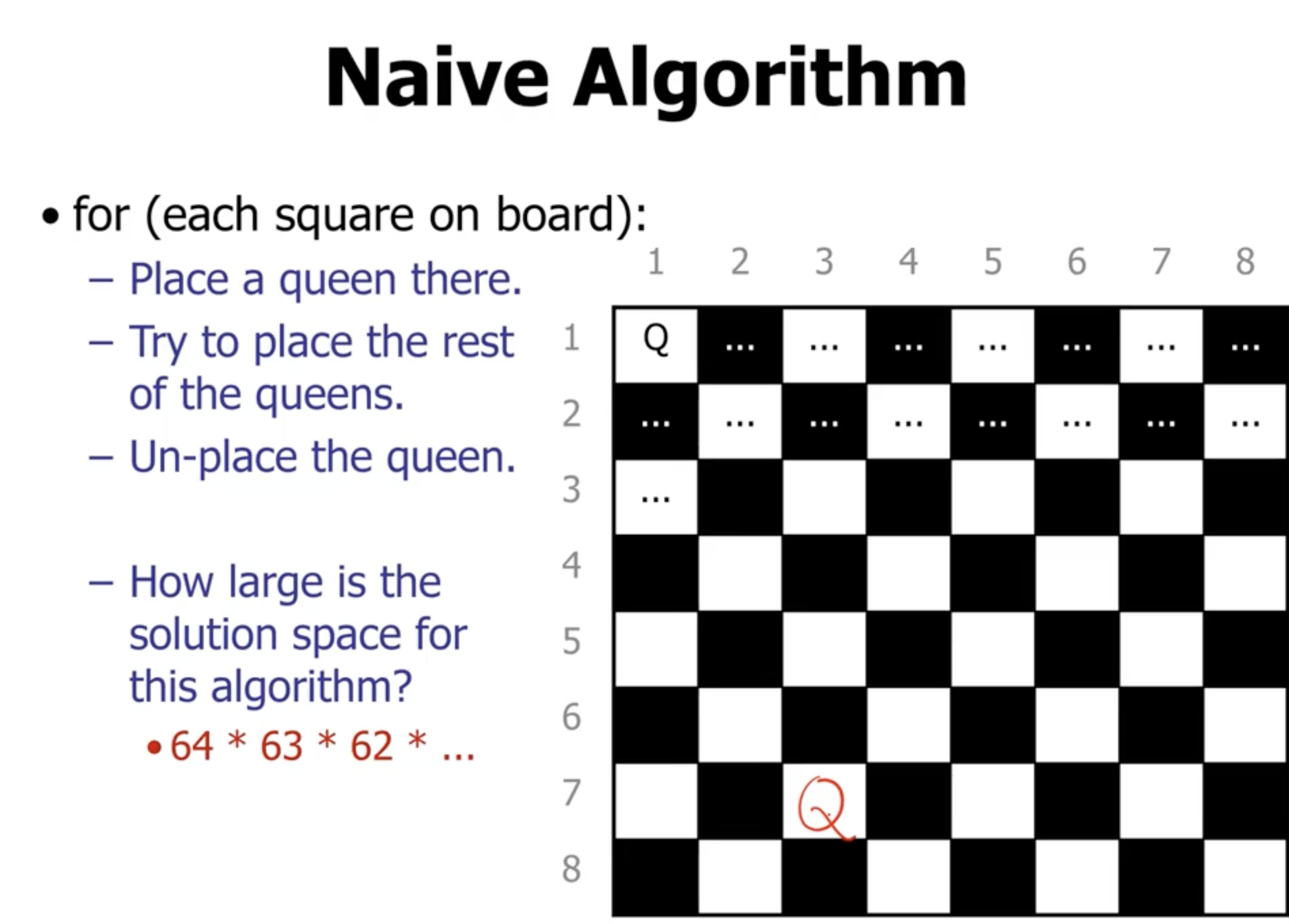
This results in a terrible complexity of \( O((n^2)!) \)

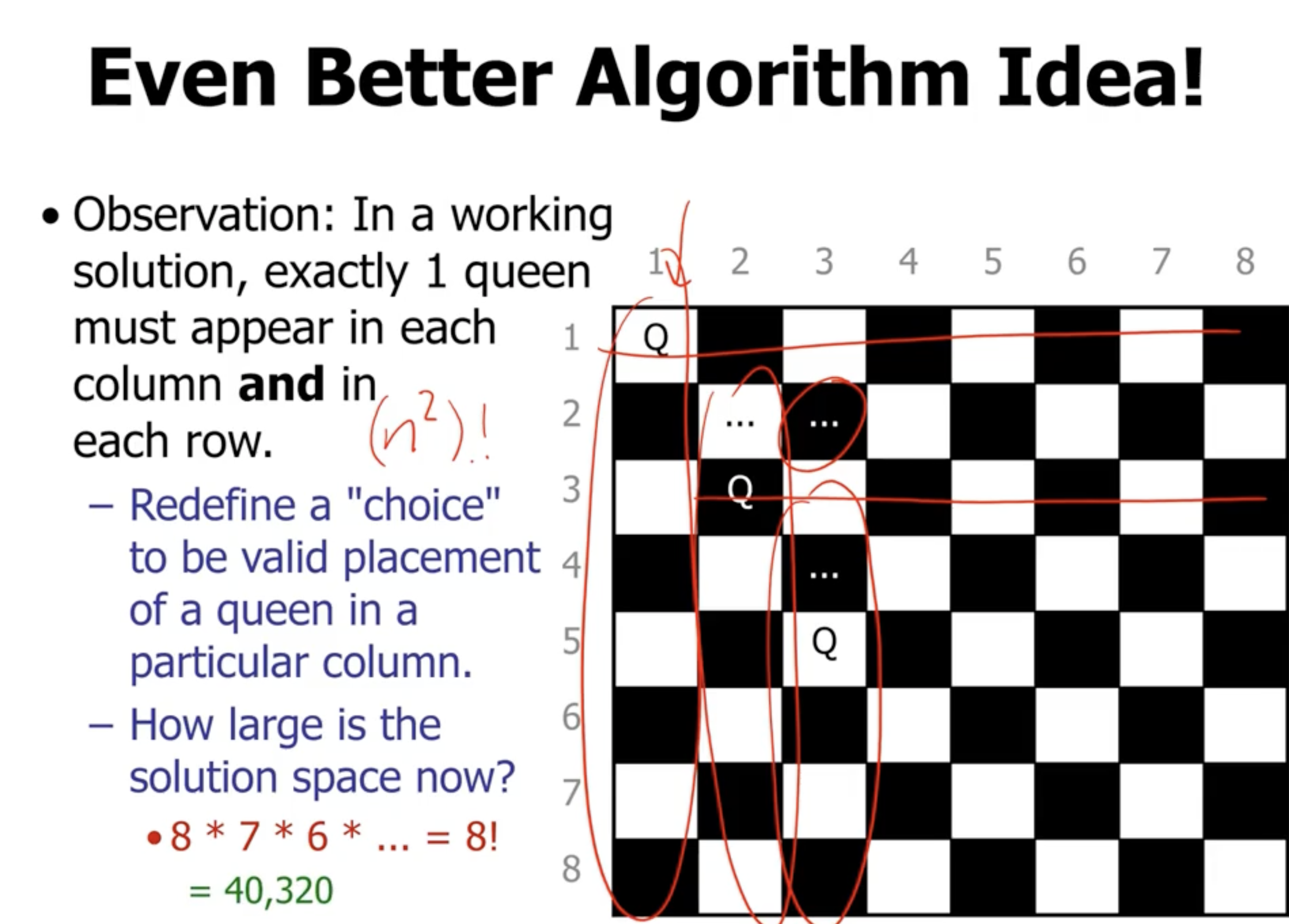
For really small \( n \) this will work, (somewhere around \( n < 15 \) ), despite the complexity being \( O(n!) \) .
My solution in python
# Place n queens on a nxn chess board, where no queen can attack another
def make_board(n):
return [[0 for i in range(n)] for i in range(n)]
def print_board(board):
for row in board:
for col in row:
print(str(col) + " ", end="")
print()
def place_queens(board):
n = len(board)
cols = [i for i in range(n)]
def placeable(row, col):
# check row
for r in board[row]:
if r == 1:
return False
# check col
for c in board:
if c[col] == 1:
return False
# check diags
## up left
r, c = row - 1, col - 1
while r > -1 and c > -1:
if board[r][c] == 1:
return False
else:
r -= 1
c -= 1
## up right
r, c = row - 1, col + 1
while r > -1 and c < n:
if board[r][c] == 1:
return False
else:
r -= 1
c += 1
## down left
r, c = row + 1, col - 1
while r < n and c > -1:
if board[r][c] == 1:
return False
else:
r += 1
c -= 1
## down right
r, c = row + 1, col + 1
while r < n and c < n:
if board[r][c] == 1:
return False
else:
r += 1
c += 1
# valid
return True
def drop(l, item):
new = l.copy()
new.remove(item)
return new
def _place_queens(row, cols):
if len(cols) == 0:
print("SOLUTION:")
print_board(board)
exit(0) # remove to find ALL solutions
else:
for col in cols:
if placeable(row, col):
# choose
board[row][col] = 1
# explore
_place_queens(row + 1, drop(cols, col))
# unchoose
board[row][col] = 0
_place_queens(0, cols)
if __name__ == '__main__':
board = make_board(8)
place_queens(board)
Output
SOLUTION:
1 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0
0 0 0 0 0 0 1 0
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
Sudoku #

My solution in Python
# Sudoku puzzle solver
def make_sudoku_board():
return [
[5, 3, 0, 0, 7, 0, 0, 0, 0],
[6, 0, 0, 1, 9, 5, 0, 0, 0],
[0, 9, 8, 0, 0, 0, 0, 6, 0],
[8, 0, 0, 0, 6, 0, 0, 0, 3],
[4, 0, 0, 8, 0, 3, 0, 0, 1],
[7, 0, 0, 0, 2, 0, 0, 0, 6],
[0, 6, 0, 0, 0, 0, 2, 8, 0],
[0, 0, 0, 4, 1, 9, 0, 0, 5],
[0, 0, 0, 0, 8, 0, 0, 7, 9],
]
def print_board(board):
for row in board:
for col in row:
print(col, end=" ")
print()
def solve(board):
def get_nums(row, col):
nums = [i for i in range(1, 10)]
# eliminate nums from row
for r in board[row]:
try:
nums.remove(r)
except:
pass
# eliminate nums from col
for r in board:
try:
nums.remove(r[col])
except:
pass
# eliminate nums from matrix
mat_row, mat_col = 0, 0
if row < 3:
mat_row = 0
elif row < 6:
mat_row = 3
else:
mat_row = 6
if col < 3:
mat_col = 0
elif col < 6:
mat_col = 3
else:
mat_col = 6
for i in range(mat_row, mat_row + 3):
for j in range(mat_col, mat_col + 3):
try:
nums.remove(board[i][j])
except:
pass
return nums
def _solve(row, col):
if row == 8 and col == 8:
print("\nSOLUTION:")
print_board(board)
exit(0)
if board[row][col] == 0:
for t in get_nums(row, col):
# choose
board[row][col] = t
# explore
_solve(row if col < 8 else row + 1, (col + 1) % 9)
# unchoose
board[row][col] = 0
else:
_solve(row if col < 8 else row + 1, (col + 1) % 9)
_solve(0, 0)
if __name__ == '__main__':
board = make_sudoku_board()
print_board(board)
solve(board)
Output
5 3 0 0 7 0 0 0 0
6 0 0 1 9 5 0 0 0
0 9 8 0 0 0 0 6 0
8 0 0 0 6 0 0 0 3
4 0 0 8 0 3 0 0 1
7 0 0 0 2 0 0 0 6
0 6 0 0 0 0 2 8 0
0 0 0 4 1 9 0 0 5
0 0 0 0 8 0 0 7 9
SOLUTION:
5 3 4 6 7 8 9 1 2
6 7 2 1 9 5 3 4 8
1 9 8 3 4 2 5 6 7
8 5 9 7 6 1 4 2 3
4 2 6 8 5 3 7 9 1
7 1 3 9 2 4 8 5 6
9 6 1 5 3 7 2 8 4
2 8 7 4 1 9 6 3 5
3 4 5 2 8 6 1 7 9