A note on learning in this class #
On different levels of learning

We will strive for about 60% of problems being level 3.
When working on a problem, there can be 3 outcomes
- could solve it
- could not solve it
- solved, but incorrect
If solved incorrectly, tracing back to the exact part that went wrong can be really beneficial.
Methods of proof cont. #
An easy starting example #
Suppose that \( x > 3 \) , is \( x^2-2y > 5 \) ?
Note: Remember, this is a universal statement. So it is asking whether that is true for all \( x \) and \( y \) .
The first thing we can try to do is disprove the statement. We need to come up with values that show that this statement is false. Lets say we let \( x=4 \) , and \( y=10 \) , so
\[\begin{aligned} 4^2 - 2(10) &> 5 \\ -4 &\not > 5 \end{aligned}\]So, by counter example, it is not true for all \( x \) and \( y \) values.
Example 2 #
Suppose that \( a,b \in \mathbb{R} \) . If \( 0 < a < b \) , then \( a^2 < b^2 \) . We can let
\[\begin{aligned} p &= 0 < a < b \\ q &= a^2 < b^2 \end{aligned}\]The question is saying that “if \( p \) then \( q \) .”
We can start by trying to see if \( p \to q \) is true. Lets start with \( p \) , and see if we can get to \( \)
\[\begin{aligned} 0 < a &< b\\ a \cdot a &< b \cdot a \\ a^2 &< ab\\ \end{aligned}\]Also,
\[\begin{aligned} a \cdot b &< b \cdot b \\ ab &< b^2 \end{aligned}\]And we can plug it back in:
\[\begin{aligned} a^2 < ab < b^2 \\ a^2 < b^2 \end{aligned}\]Example 3 #
Suppose that \( a,b,c \in \mathbb{R} \) and \( a > b \) . If \( ac \leq bc \) , then \( c \leq 0 \) .
Looking at the direct method to solve this
\[\begin{aligned} ac \leq bc \to c \leq 0 \end{aligned}\]show that it may be difficult to prove that given the constraints above. We can look at the opposite direction (remembering that \( a > b \) ),
\[\begin{aligned} c \leq 0 \to ac \leq bc \end{aligned}\]to see that the problem is more doable.
If \( c = 0 \) , then
\[\begin{aligned} ac = bc \end{aligned}\]and if \( c < 0 \) , then
\[\begin{aligned} c( a > b) = ac \leq bc \end{aligned}\]So in this case it was easier to prove \( \neg q \to \neg p \) .
Example 4 #
Show that for any natural number \( n \) ,
\[\begin{aligned} 2^0 + 2^1 + \cdots + 2^n = 2^{n+1} - 1 \end{aligned}\]If we call this function \( p(n) \) , then the problem is really asking \( \forall n \in \mathbb{N} : p(n) \) (is true). For this problem, we can try mathematical induction.
Since the domain for this is natural numbers, we can start from 0 and increase. \( p(0) \) should be the base case, lets see:
\[\begin{aligned} p(0) &= 2^0 = 2^{0+1} - 1 & \text{true}\\ \end{aligned}\]The inductive step: Suppose that \( p(n) \) is true, we show that \( p(n+1) \) is true.
\[\begin{aligned} p(n) &= 2^0 + 2^1 + \cdots + 2^n = 2^{n+1} - 1 \\ p(n+1) &= 2^0 + 2^1 + \cdots + 2^{n+1} = 2^{(n+1)+1} - 1 \end{aligned}\]Lets start with the left side of \( p(n+1) \) , and substitute in \( p(n) \)
\[\begin{aligned} \overbrace{\underbrace{2^0 + 2^1 + \cdots + 2^n}_{p(n)} + 2^{n+1}}^{p(n+1)} &= (2^{n+1} - 1) + 2^{n+1} \\ &= 2 \cdot 2^{n+1} - 1 \\ &= 2^{(n+1)+1} - 1 \end{aligned}\]So, by mathematical induction it is true.
Example 5 #
Show that \( \forall n \geq 5 : 2^n > n^2 \) .
Note: Since the variable is named \( n \) , and \( n \) starts as being equal to or greater than a natural number, we can assume that \( n \) is also a natural number. If \( n \) was real, the problem would most likely explicitly state that \( n \) is real.
Lets use mathematical induction for this problem, with the base case being \( p(5) \) :
\[\begin{aligned} p(5) &= 2^5 > 5^2 \\ &= 32 > 25 &\text{true} \end{aligned}\]Inductive step: Assume \( p(n) \) is true, show that \( p(n+1) \) is true,
\[\begin{aligned} p(n) &= 2^n > n^2 \\ p(n+1) &= 2^{n+1} > (n+1)^2 \end{aligned}\]Lets start with the left side of \( p(n+1) \) , and substitute in \( p(n) \)
\[\begin{aligned} 2^{n+1} = 2 \cdot 2^n &> 2 \cdot n^2 = 2 n^2 \\ \end{aligned}\]Lets see if we can make \( 2n^2 \) as similar to \( (n+1)^2 \) as possible
\[\begin{aligned} 2n^2 \geq n^2 + 2n + 1 \\ n^2 \geq 2n + 1 \\ n \geq 2 + \frac{1}{n} \end{aligned}\]So as long as
\[\begin{aligned} n \geq 2 + \frac{1}{5} \end{aligned}\]We can argue that since
\[\begin{aligned} n \geq 2 + 1 \geq 2 + \frac{1}{n} \end{aligned}\]So,
\[\begin{aligned} 2^{n+1} \geq (n+1)^2 \end{aligned}\]Example 6 #
Show that for any \( n > 0 \) , a \( 2^n \times 2^n \) grid square with any one square removed can be covered with L shaped tiles.
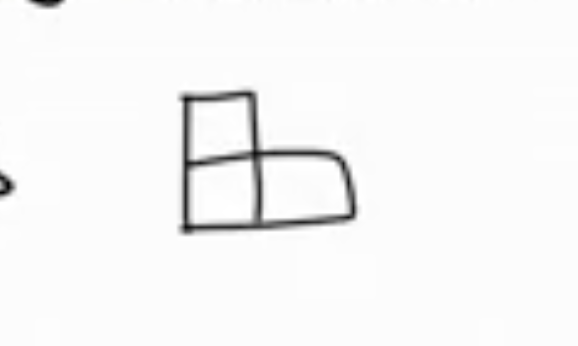
So for \( n = 1 \) :
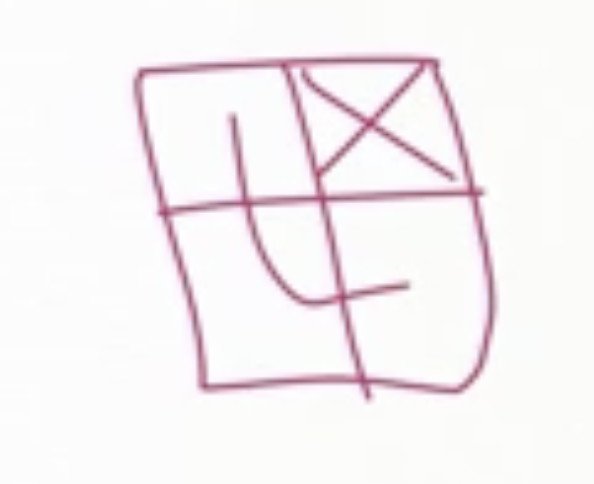

The domain of this problem is all the squares made up of \( 2^n \times 2^n \) , with the base case being \( n = 1 \) . So we can use mathematical induction.
The base case for the \( 2 \times 2 \) grid shows that if any of the squares are removed, the rest can be covered with an L shape. We can show all 4 cases:

The inductive step: lets assume that it is true for \( 2^n \times 2^n \) grid sizes, lets show it is true for \( 2^{n+1} \times 2^{n+1} \) grid sizes also.
If we think of one square being removed in the top right quadrant, we can cover that with an L shape.
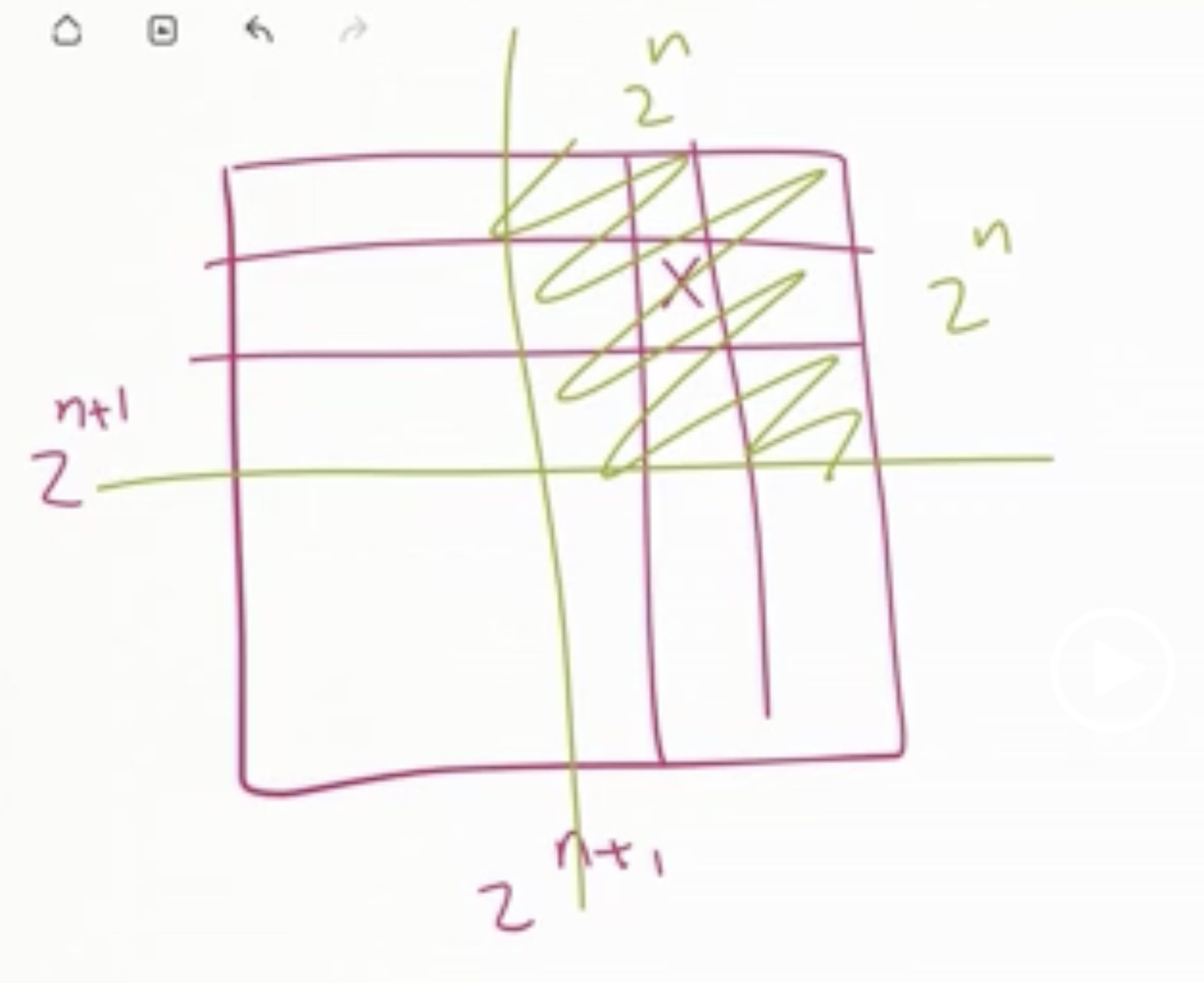
Then we can think of that entire quadrant as being the square removed, and cover the middle 3 with an L shape.
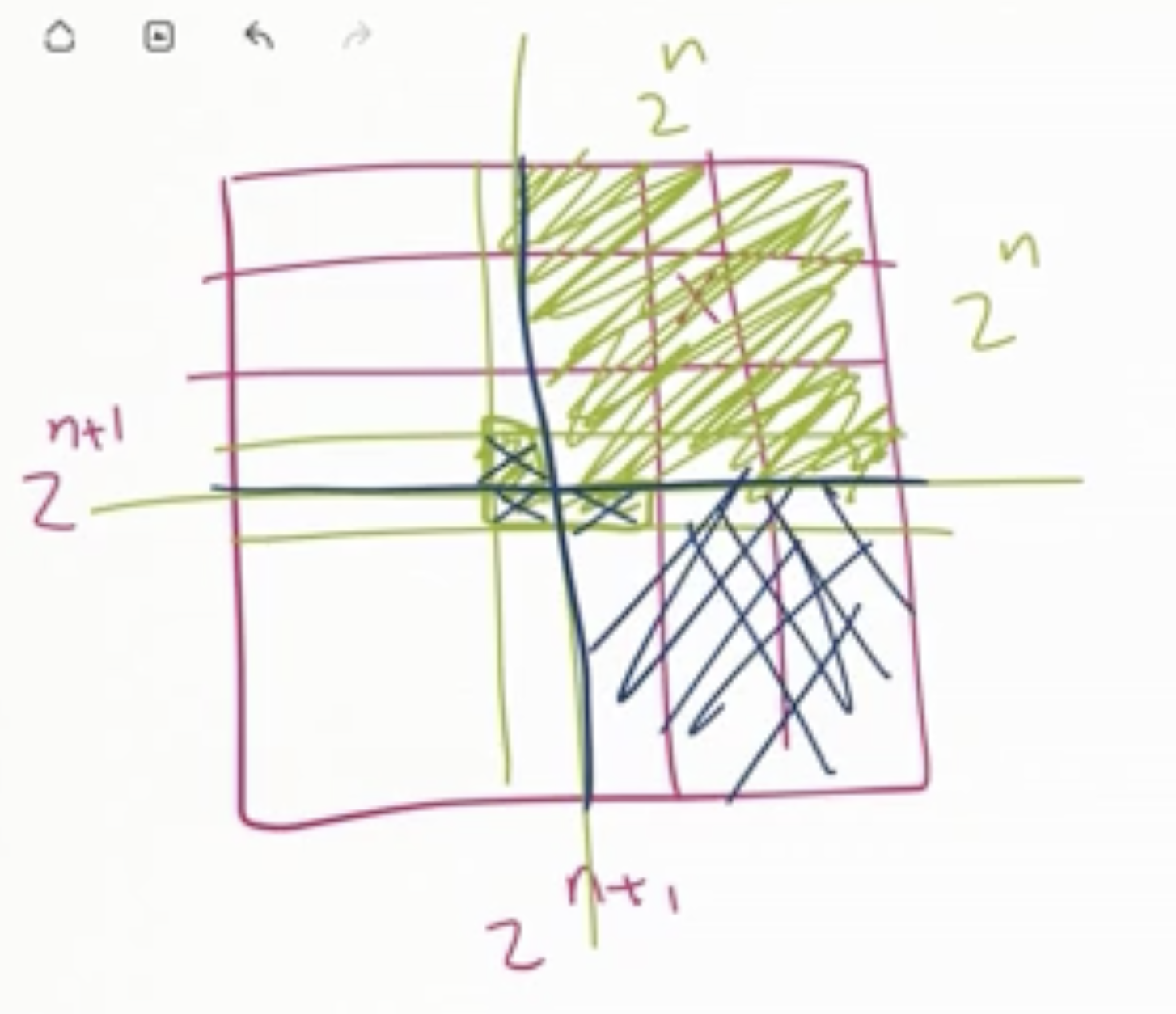
The rest of each quadrant can now be covered with another L shape each.
Asymptotic analysis #
File: 140-1.pdf



Anything worse than polynomial time, generally is not practical.
If we double the input size in a polynomial-time function, the algorithm should only slow down by some constant factor, ie
\[\begin{aligned} n^2 \to (2n)^2 \to 4n^2 \end{aligned}\]Compare with a non-polynomial run time:
\[\begin{aligned} 2^n \to 2^{2n} \to 2^n \cdot 2^n \end{aligned}\]this shows that it does not increase by a constant factor, therefore it is not a polynomial time.


Execution time depends greatly on the hardware that the program is running on.

Example 1 #

The total cost of algorithm 1 is \( c_1 N \)
The loop in algorithm 2 will run \( N+1 \) times, and the body of the loop will run \( N \) times, so the total cost is \( (c_2 + c_1) N + c_2 \)

The outer loop runs \( N+1 \) times, and the inner loop run \( (N+1)N \) . The body of the inner loop will run \( N \cdot N \) times. So, the total cost is
\[\begin{aligned} c_1 + c_2(N+1) + c_2 N (N+1) + c_3 N^2 \end{aligned}\]Comparing algorithms #
When analyzing an algorithm, we will go with a rough measure of the total cost. This is usually the highest degree, the rate of growth, of the function.


The rate of growth is dominated by the cost of elephants because they cost a lot more. So the rate of growth can be approximated by just looking at the cost of elephants.
Asymptotic notation #

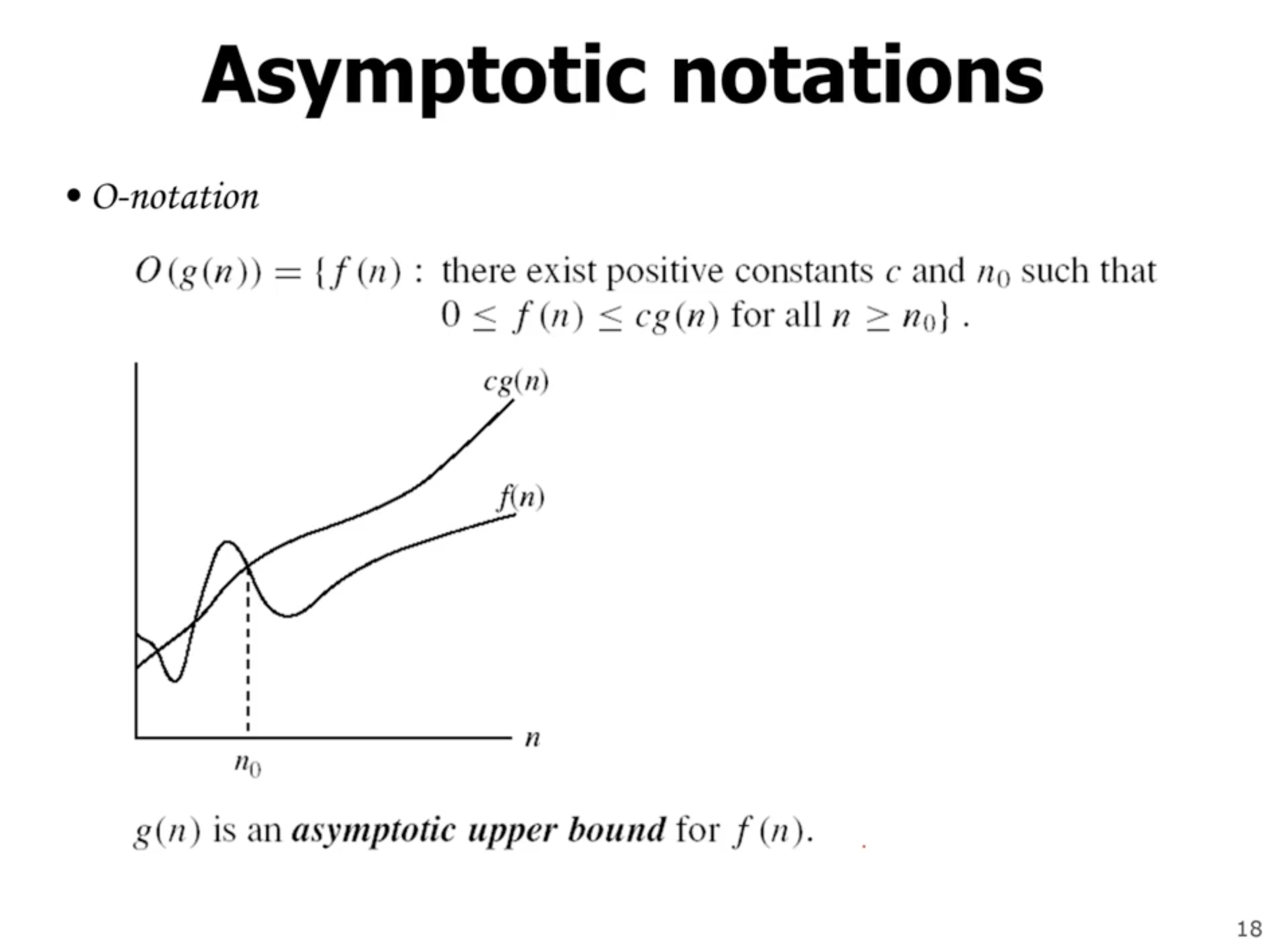
- Big \( O \) , upper bound
- Big \( \Theta \) , exact bound
- Big \( \Omega \) , lower bound
When looking for a tight bound, look for the Big \( \Theta \) .

If we have
\[\begin{aligned} 2n^2 - n + 5 \end{aligned}\]the \( n^2 \) dominates as \( n \to \infty \) . So the runtime is \( O(n^2) \) .

While the algorithms may start with \( f_B \) being faster, once \( n \) gets large enough it will grow faster than \( f_A \) .

Note: If we have \[\begin{aligned} 2n^2 + 5 \lg n \end{aligned}\]the exponential term will always dominate the logarithmic term, so \( O(n^2) \) .



Example problems #
Prove that \( 2n^2 = O(n^3) \) .
We want to find \( c \) and \( n_0 \) such that \( \forall n \geq n_0: 0 \leq f(n) \leq c(g(n)) \) .
So,
\[\begin{aligned} 2n^2 &\leq c n^3 \end{aligned}\]and solve for \( c \) .
\[\begin{aligned} 2 &\leq cn \\ \frac{2}{n} &\leq c \end{aligned}\]So this works when \( c = 2 \) and \( n = 1 \) , and up. So our initial \( n \) value that works is \( 1 \) , so \( n_0 = 1 \) . This makes the equality true for all values higher than the initial.
Note: The functions can cross each other, but after the value \( n_0 \) , the functions no longer cross.
Prove that \( n^2 = O(n^2) \) .
\[\begin{aligned} n^2 \leq cn^2 \to c \geq 1 \end{aligned}\]So \( c = 1 \) and \( n_0 = 1 \) .
Prove that \( 1000n^2 + 1000n = O(n^2) \) .
\[\begin{aligned} 1000n^2 + 1000n \leq cn^2 \end{aligned}\]This doesn’t show an easy value for \( c \) . So we can think of it as
\[\begin{aligned} 1000n^2 + 1000n &\leq 1000n^2 + 1000 n^2 \\ &= 2000 n^2 \end{aligned}\]This works when \( n \geq 1 \) .
So our \( c = 2000 \) , and \( n_0 = 1 \) .
Note: So the general idea here was to transform the \( n \) term so it can be combined, and it is easier to see what the \( c \) value should be.
Prove that \( n = O(n^2) \) .
\[\begin{aligned} n &\leq cn^2 \\ cn &\geq 1 \end{aligned}\]So when \( c = 1 \) and \( n_0 = 1 \) it is true.
Show that \( 30n + 8 \) is \( O(n) \) .
\[\begin{aligned} 30n + 8 &\leq cn \\ 30n + 8 &\leq 30n + n \\ 30n + 8 &\leq 31n \end{aligned}\]Note that this is only true when \( n > 8 \) , so our values are \( c = 31 \) and \( n_0 = 8 \) .
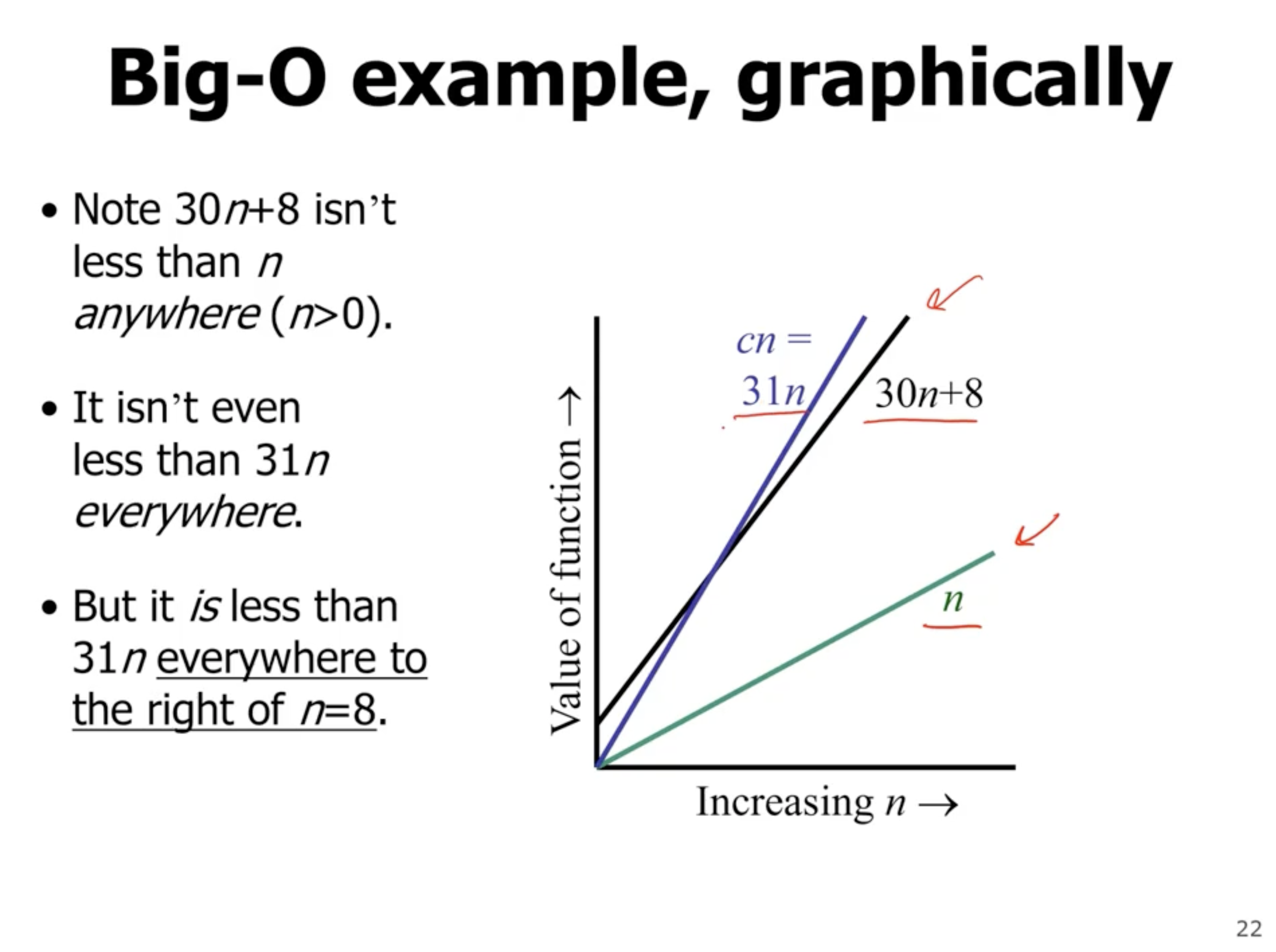
The point where they cross is \( n_0 \) .
No uniqueness #

Trying to prove something that is not true #
Lets try to prove \( 4n^2 = O(n) \) .
\[\begin{aligned} 4n^2 &\leq cn \\ 4n &\leq c \end{aligned}\]Since \( n \) does not have an upper bound, we cannot have our constant \( c \) always larger than an arbitrarily large \( n \) . This is a contradiction.
Show that \( n^2 - 2n + 3 \lg n = O(n^2) \) .
\[\begin{aligned} n^2 - 2n + 3 \lg n &\leq cn^2 \\ &\leq n^2 + 3 \lg n \\ &\leq n^2 + 3n \end{aligned}\]Which we can do because
\[\begin{aligned} \lg n \leq n \\ n \leq 2^n \end{aligned}\]So \( n_0 = 1 \) , and we can see this is true by \( 1 \leq 2^1 = 2 \) . The terms can combine to get \( c = 4 \) :
\[\begin{aligned} &\leq n^2 + 3 n^2 \\ &\leq 4n^2 \end{aligned}\]