Lexical specification to DFA #
WORD: aa+aaa
OTHER: aa*
Heres an NFA for each regular expression:

So now we can take the NFA and make a DFA out of it. Recall, the scanner will need to use a DFA.

Then we can label the accept states with the lexeme types:

So for example, to scan this sequence:
a aa aaa aaaa

Nullablity #
A non-terminal, or a sequence of non-terminals, is nullable if the empty string can be derived from it.
Consider the grammar
\( A \to AB \mid \lambda \\ B \to aA\)We look at this and reason what is nullable. Since \( A \) goes to \( \lambda \) , \( A \) is nullable. We can also tell that \( B \) is not nullable because the single production for \( B \) has a terminal character in it. Once we replace \( B \) there is no way to remove the terminal, so it is not nullable.
We can also use a fixed-point algorithm to tell whether something is nullable. Sometimes a grammar is complicated enough where you can’t just tell what is nullable.
The algorithm is as follows:
- Write down all of the right hand sides of your productions
- Write down all of the left hand sides, the non-terminals
We can initially consider all of them false, as in non of them are nullable.

We can then look at the non-terminals and see if they are nullable (true or false), and fill in a new column. Likewise, we can turn any of the non-terminals true if any of their right hand sides are nullable.

We continue this until there is no change between the columns. We will continue until we reach a fixed-point (a point where nothing changes). Once we reach this state there will be no iterations done because nothing will continue changing.
Because at least one right hand side for \( A \) is true, that means that \( A \) can be nullable.
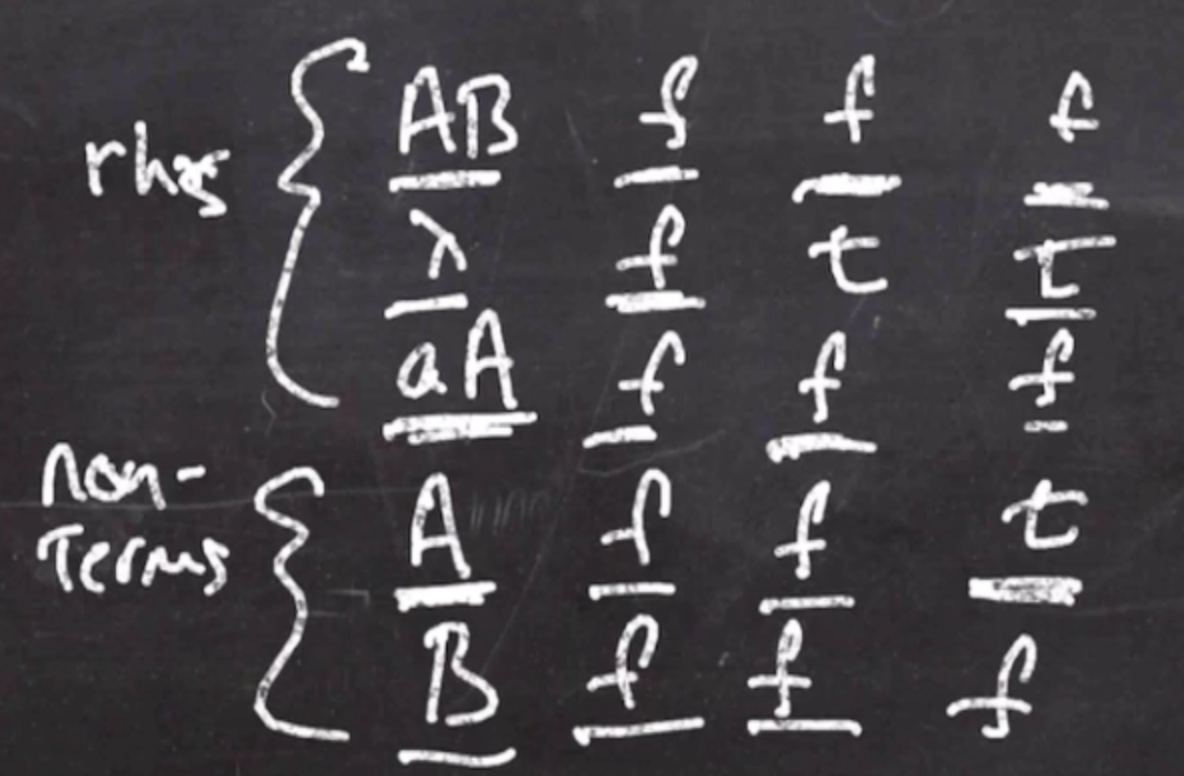

After another iteration, there has been no change, so we are done.
We can tell from the column that \( A \) and \( \lambda \) are nullable.
First sets #
First is the set of all characters that the string could start with if its derived.
For example:
\( A \to aA \mid \lambda \)The language of a is \( L(A) = \{\lambda, a, aa, aaa, \ldots \} \) . The empty string doesn’t have a first character so we ignore it, but all other strings start with an \( a \) .
So \( \text{First } (A) = \{a\} \)
Now consider
\( A \to aA \mid \lambda \mid bA \) .
Now the language is \( L(A) = \{ \lambda, a, b, aa, ab, ba, bb, \ldots \}\) . So now the strings can start with an \( a \) or a \( b \) .
So \( \text{First } (A) = \{a, b\} \)
It is also useful to tell the first of multiple languages, i.e.

If \( A \) is not nullable, then \( \text{First } (AB) \) will be equal to \( \text{First } (A) \) . If \( A \) is nullable, then we can say that \( \text{First } (AB) = \text{First } (A) \cup \text{ First } (B)\) .
There is a fixed-point algorithm to determine if you can’t see it initially:
Consider
\( A \to Ba \mid Cb \\ B \to b \mid \lambda \\ C \to c \mid \lambda\)We can tell that \( B \) and \( C \) are nullable, but \( A \) is not.
First we can write down all the right hand sides of the productions and start them as the empty set \( \{\} \) . Also, we write down the left hand sides at the bottom.

The new column being built will be based on the prior column, and we determine if anything will be added to its first set. Also, consider nullability when checking. \( B \) is nullable, so the string could start with an \( a \) .
Also consider the non-terminal left hand sides and copy from the upper sets.


This continues until the columns don’t change anymore.

After one more iteration, there is no change so we are done.
Unified algorithm #
Recall the rules of the previous algorithms

Consider this grammar
\( T \to R \mid aTc \\ R \to bR \mid \lambda\)We can tell that we will have an equal number of \( a \) s and \( c \) s, then we will have \( b \) in the middle, any number of times.
This is generating the language \( \{a^n b^m c^n : n,m \geq 0\} \) .
So which of the above rules apply?
Lets first look at \( T \to R \)
\( \text{First } (R) \subseteq \text{ First } (T) \\\) \( \text{Follow } (T) \subseteq \text{ Follow } (R) \)
Now lets look at \( T \to aTc \\ \)
\( \{a\} \subseteq \text{ First } (T) \\\) \(\{c\} \subseteq \text{ Follow } (T) \)
Note that \( T \) and \( R \) are nullable.
Lets do \( R \to bR \\ \)
\( \{b\} \subseteq \text{ First } (R) \\ \) \( \text{ Follow } (R) \subseteq \text{ Follow } (R) \)
The last one doesn’t actually produce any information, any subset is of itself. This is a tautology.
We also have to consider \( R \to \lambda \) , which does not produce anything.
We also usually add a new start symbol followed by the \( \$ \) to indicate the end of the input.
\( T' \to T\$ \)This is to force checking that the whole input is in the language, not just a prefix. Also note that this produces the rule
\( \{ \$ \} \subseteq \text{ Follow } (T) \)Now we can use the fixed-point algorithm to find the specific sets. We have to determine the first sets and follow sets of both \( T \) and \( R \) .
\( \text{ First } (T) = \{a,b\}\\ \) \( \text{ First } (R) = \{b\}\\ \) \( \text{ Follow } (T) = \{c, \$\}\\ \) \( \text{ Follow } (R) = \{c, \$\}\\ \)
Now that we have the minimum sets that satisfy the rules, we can create a prediction table.
| Production | \( \text{First(right hand side)} \) | If right handside is nullable, \( \text{ Follow(left hand side) }\) |
|---|---|---|
| \( T \to R \) | \( \{b\} \) | \( \{c, \$\} \) |
| \( T \to aTc \) | \( \{a\} \) | |
| \( R \to bR \) | \( \{b\} \) | |
| \( R \to \lambda \) | \( \{\} \) | \( \{c, \$\} \) |
We can use this table for predictive descent by looking at the rows for each non-terminal and making sure the sets are disjoint.
Recursive-descent predictive-parsing example #

















An example parser in racket #
Consider the language
\( S' \to S \$ \\ S \to aSz \mid bSy \mid \lambda\)#lang racket
; next : list -> string or false
; if list not empty and first item a string, eval to first item, else false
; Examples:
; (next '("a" "b" "c")) -> "a"
; (next '("a" 2 3)) -> "a"
; (next '(1 "b" "c")) -> false
; (next "a") -> false
; (next '()) -> false
(define (next toks)
(cond ((empty? toks) false)
((not (list? toks)) false)
((string? (first toks)) (first toks))
(else false)))
(next '("a" "b" "c"))
(next '("a" 2 3))
(next '(1 "b" "c"))
(next "a")
(next '())
; match : list item -> list or false
; if first item of list equals item return rest of list, else false
; Examples:
; (match '("a" "b" "c") "a") -> '("b" "c")
; (match '("a" "b" "c") "b") -> false
; (match '("a") "a") -> '()
; (match '() "a") -> false
; (match false "a") -> false
(define (match toks tok)
(cond ((empty? toks) false)
((not (list? toks)) false)
((equal? tok (first toks)) (rest toks))
(else false)))
(match '("a" "b" "c") "a")
(match '("a" "b" "c") "b")
(match '("a") "a")
(match '() "a")
(match false "a")
; S' → S$
; S → aSz | bSy | λ
(define (parseS toks)
(cond ((not (list? toks)) false)
((empty? toks) toks)
((equal? (first toks) "a") (match (parseS (match toks "a")) "z"))
((equal? (first toks) "b") (match (parseS (match toks "b")) "y"))
(else toks)))
; First(S') = {a,b,$}. On any of these three, (parseS toks) and verify result is end-of-input.
(define (parseSprime toks)
(cond ((not (list? toks)) false)
((empty? toks) (equal? (parseS toks) empty)) ; $ predicts S' -> S$
((equal? (next toks) "a") (equal? (parseS toks) empty)) ; a predicts S' -> S$
((equal? (next toks) "b") (equal? (parseS toks) empty)) ; b predicts S' -> S$
(else false)))
; these should be true
(parseSprime '("a" "b" "y" "z"))
(parseSprime '("a" "a" "z" "z"))
(parseSprime '("a" "z"))
(parseSprime '("b" "y"))
; these should be false
(parseSprime '("a" "b"))
(parseSprime '("b" "b"))