Parse trees and Ambiguity #
Parse trees are graphical representations of what each non-terminal produces during a derivation.
An example of a parse tree:
\( S \to AB \\ A \to aaA \mid \lambda \\ B \to bbB \mid b\)This grammar produces all strings that have an even number of \( a \) ’s and an odd number of \( b \) ’s.
So we can prove that \( aabbbbb \) is in the language by showing a derivation:
\( S \to AB \to AbbB \to AbbbbB \to Abbbbb \to aaAbbbbb \to aabbbbb\)So to build a parse tree, at each production we draw a representation of what got replaced.
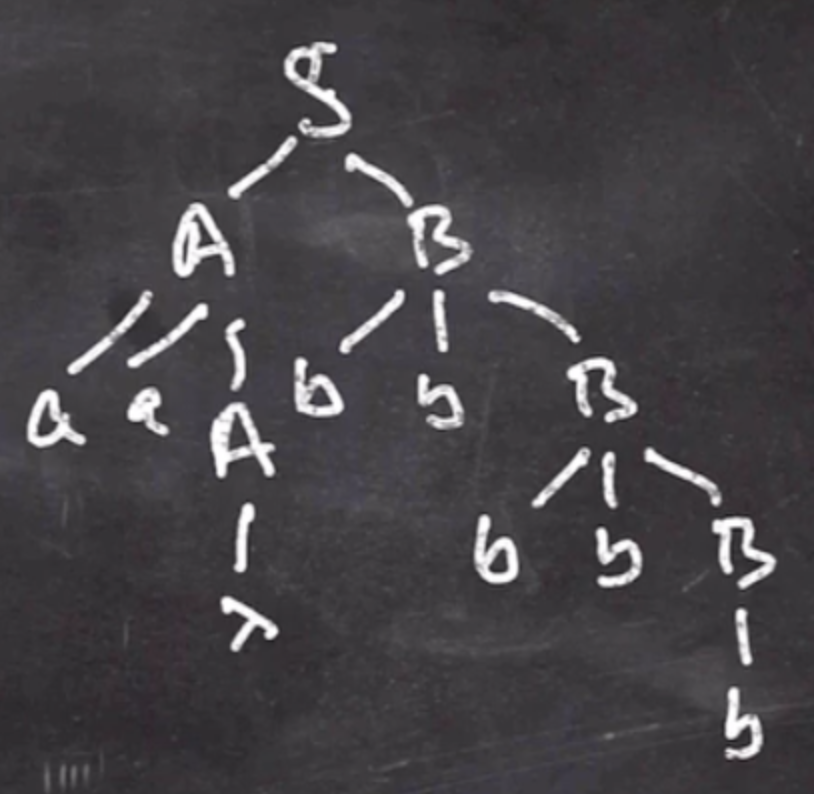
It doesn’t matter if we did the \( A \) stage or the \( B \) stage first, it would end in the same parse tree.
Note: The fringe (the leaves of this tree concatenated together) is the intermediate string at each step during the derivation. When the entire parse tree is drawn, the fringe is the output string.
Ambiguous grammar #
A grammar is ambiguous if and only if there exists a string in the language of the grammar with 2 different parse trees.
An example of an ambiguous grammar is:
\( S \to AA \\ A \to aA \mid \lambda\)To prove that this is ambiguous, we can show 2 different derivations for \( aaa \) :


Since the fringes are identical, they both represent different ways to derive the string \( aaa \) , but since they are 2 different parse trees this proves that the grammar is ambiguous.
Since CFGs can represent programming languages, a parse tree represents a program. If a compiler can produce 2 different parse trees (programs) for a single source code, that is a bad thing.
Steps to show that a grammar is ambiguous #
- Choose a string
- Demonstrate two legitimate parse trees for the string
Alternatively, you can show 2 different derivations for the same string. This doesn’t always work however, with the first language we expressed above (even \( a \) ’s with odd \( b \) ’s), because since that language is non-ambiguous, it doesn’t matter which order we process the string (it makes the same parse tree).
Leftmost derivations #
If each step of the derivation converts the leftmost non-terminal, then it is impossible to show 2 different derivations in a non-ambiguous grammar.
So for example:
\( S \to AB \to aaAB \to aaB \to aabbB \to aabbbbB \to aabbbbb\)Every string in a non-ambiguous grammar will have exactly 1 string created in a leftmost derivation. However, in an ambiguous grammar, this is not the case.
So for our ambiguous grammar above, we can derive \( aaa \) using leftmost derivation:
\( S \to AA \to aAA \to aaAA \to aaA \to aaaA \to aaa\)We can show that this is ambiguous by showing another leftmost derivation of \( aaa \) :
\( S \to AA \to aAA \to aA \to aaA \to aaaA \to aaa\)