Functional Programming #

Other functions may write to this.sum, so this could be incorrect in the future.

Any loop can be turned into a recursively structured function.

Example of pow #

int pow(int x, int y)
    if (very small)
        solve directly
    else
        solve with smaller_pow

So when is exponentiation very small? This is the base case, where y = 0.

int pow(int x, int y)
    if (y == 0)
        return 1
    else
        solve with smaller_pow

Now we need to figure out the else branch, we know that x^y = x^(y-1) * x.

int pow(int x, int y)
    if (y == 0)
        return 1
    else
        return x * pow(x, y - 1)

Intro to Racket #

racket-lang.org

wescheme.org

Racket is a form of scheme, and scheme is a form of Lisp.

A method definition (which just calls the built-in sting-append).

(define (my-concat s1 s2)
    (string-append s1 s2))

So we can call this function like:

(my-concat "abc" "def")     ; "abcdef"

Lets define a strlen function:

(define (strlen s)
    (if (= 0 (string-length s))
        0
        (+ 1 (strlen (substring s 1)))))

Yes, this is calling a built in string length function, but its just displaying how a recursively called function is setup.

(strlen "")         ; 0
(strlen "a")        ; 1
(strlen "abc")      ; 3

Racket non-list examples #

Lists are used a lot as a primary data structure in lisps.

A factorial function #

(define (fact n)
    (if (= n 0)
        1
        (* n (fact (-n 1)))))

(fact 0)        ; 1
(fact 1)        ; 1
(fact 2)        ; 2
(fact 10)       ; 3628800

Fibonacci numbers #

We can utilize the cond function, used like this:

(cond (bool expr)
      (bool expr)
      ...
      (else expr))

This is equivalent to a nested if. cond goes one by one and checks each boolean expression, and if true it replaces with expr. The ... means that there can be any number of expressions to check, this is like a switch. As soon as it finds the first true it executes the replacement then ends. At least one thing has to evaluate to true otherwise you’ll get a runtime error, so we can end with an else.

(define (fib n)
    (cond ((= n 0) 1)
          ((= n 1) 1)
          (else (+ (fib (- n 1)) (fib (- n 2))))))

So we can test this:

(fib 0)         ; 1
(fib 1)         ; 1
(fib 2)         ; 2
(fib 3)         ; 3
(fib 4)         ; 5

String reverse #

If given "abc", it should go to "cba". To test for string equality we can use built in string=?, “string equal huh?”. We can use substring to cut the string down, and string-append to append. "cba" = "cb" + "a"

(define (strev s)
    (if (string=? s "")
        s
        (string-append (strev (substring s 1)) (substring s 0 1))))

We can test now:

(strev "")      ; ""
(strev "a")     ; "a"
(strev "ab")    ; "ba"
(strev "abc")   ; "cba"

There is a built in called check-expect, which we can use to test.

(check-expect (strev "abc") "cba")

When you run this, if you see nothing then it works correctly. If it fails you will see the explanation in the output.

writeSequence problem from practiceit #

Note that if you call the sequence on 8, the center is the 6 sequence, then you divide 8 but 2 and round up to get the outside number. We can explicitly change the number to a string with number->string.

(define (ws n)
    (cond ((= n 1) "1")
          ((= n 2) "11")
          (else (string-append (number->string (ceiling (/ n 2))) (ws (- n 2)) (number->string (ceiling (- n 2)))))))

So we can test this to see if its working:

(ws 1)          ; "1"
(ws 2)          ; "11"
(ws 3)          ; "212"
(ws 4)          ; "2112"

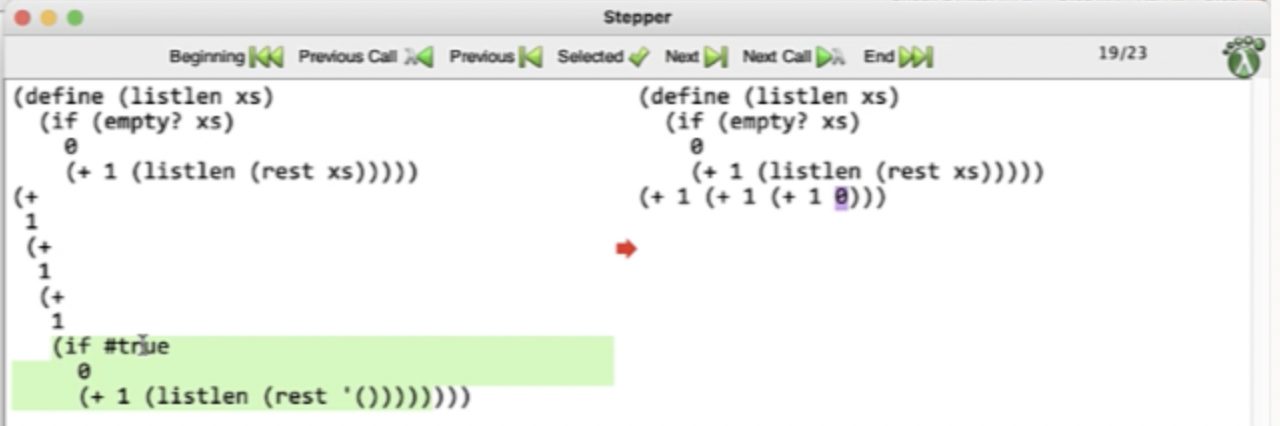
Racket under the hood #

Whenever Racket encounters a define in its top down compilation, it stores it in a table. When it calls a function call, it can be thought of as a constant replacing of definition names with its implementation. So a functions name gets replaced by its value. This is easy to think about with single value definitions, like (define n 1), but when a function is defined all the parameters are replaced in the replacement as well.

So if you have this definition:

(define (listlen xs)
    (if (empty? xs)
        0
        (= 1 ( listlen (rest xs)))))

And you call the function like:

(listlen '(1 2 3))

listlen is actually being replaced with:

(if (empty? '(1 2 3))
    0
    (+ 1 (listlen (rest '(1 2 3)))))

Which is then replaced by

(+ 1 (listlen (rest '(1 2 3))))

(+ 1 (listlen `(2 3)))

and so forth.

Debugging in DrRacket #

We can click step in DrRacket to open up a stepper window, that highlights the next substitution that will happen.

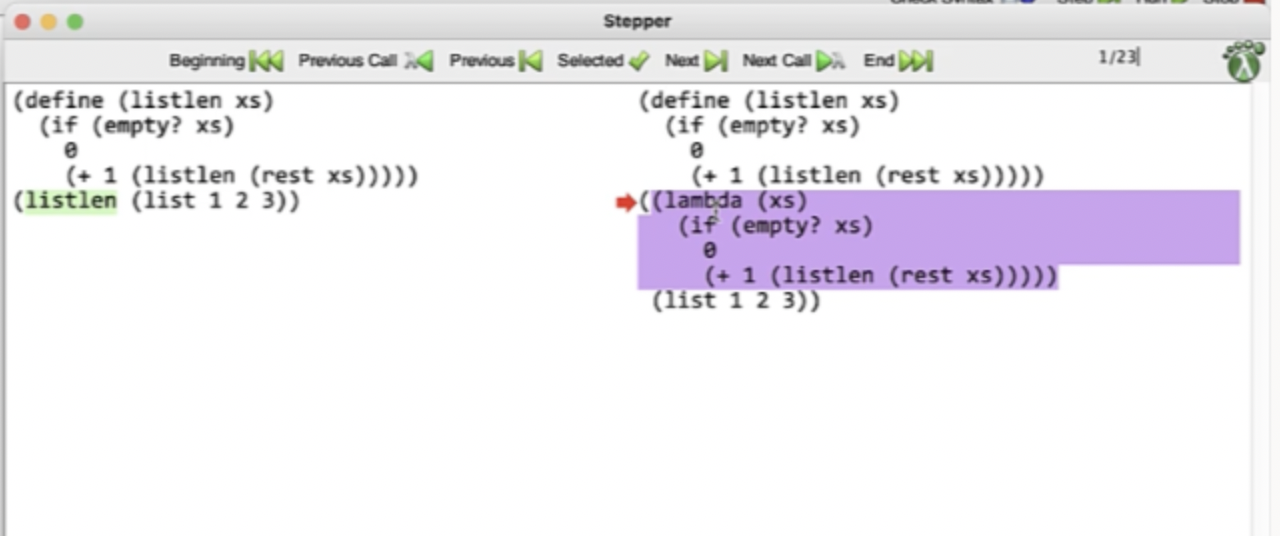
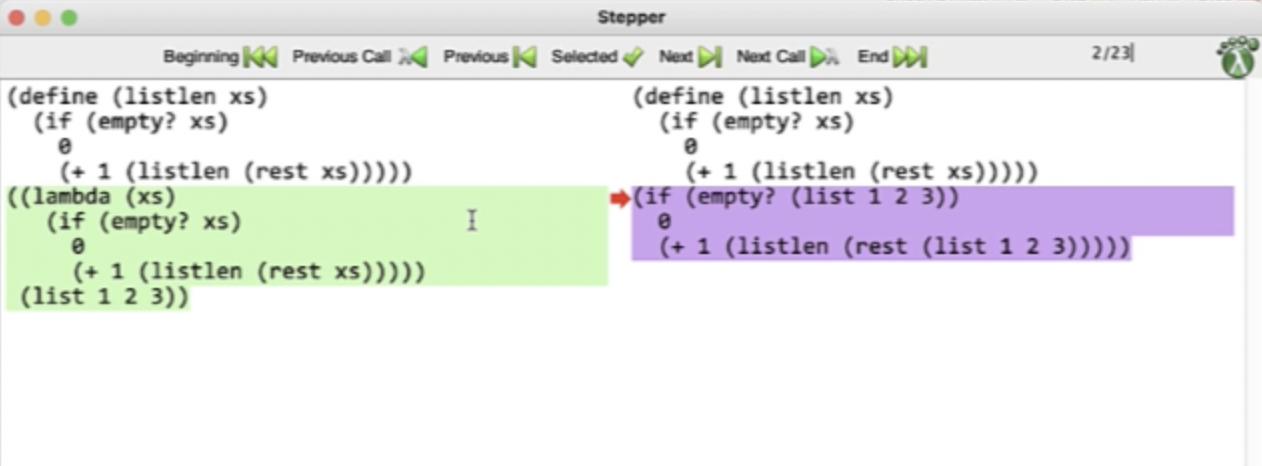
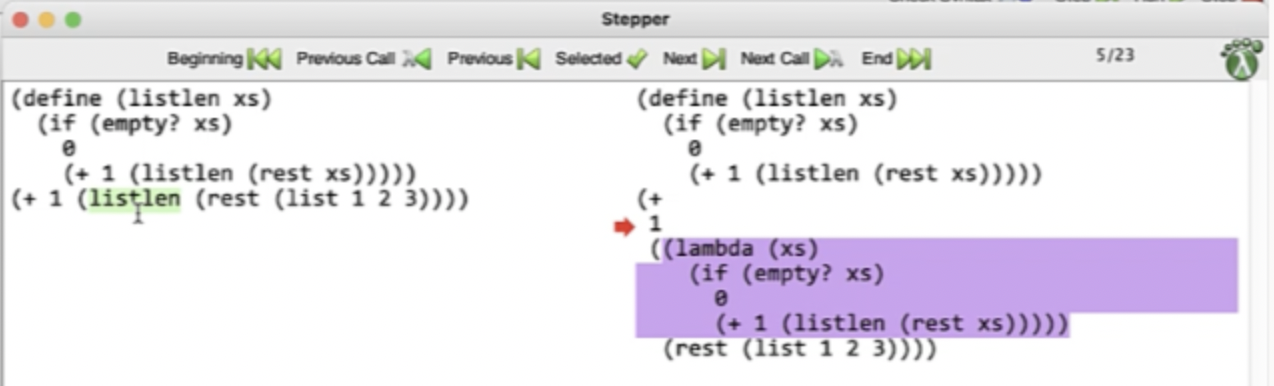
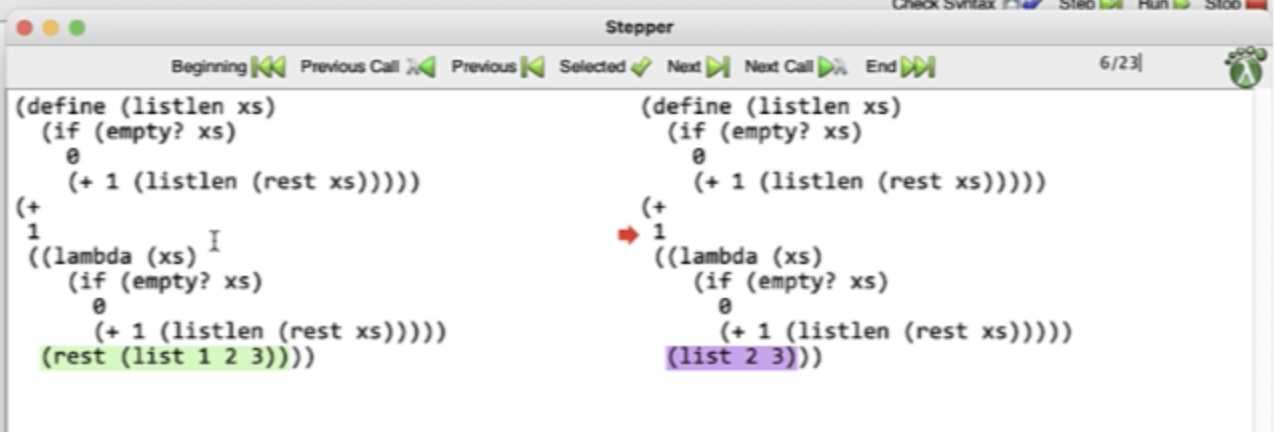
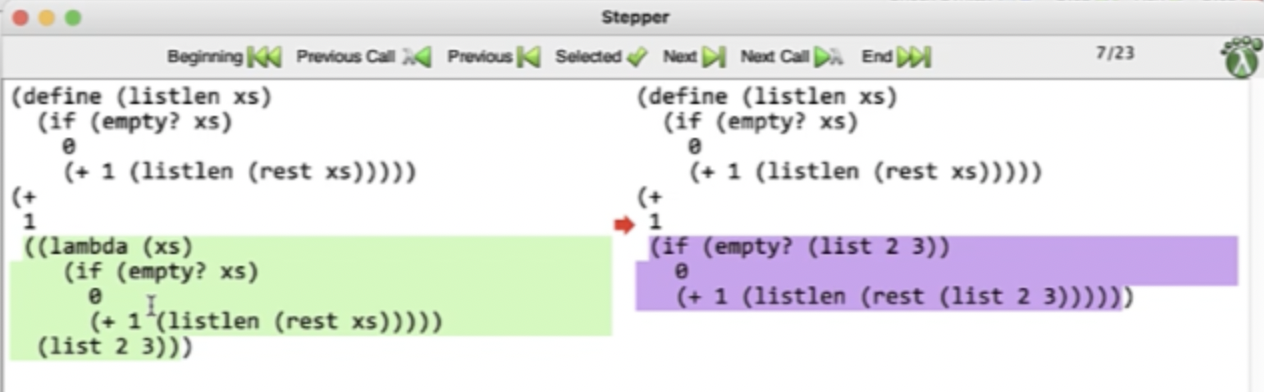
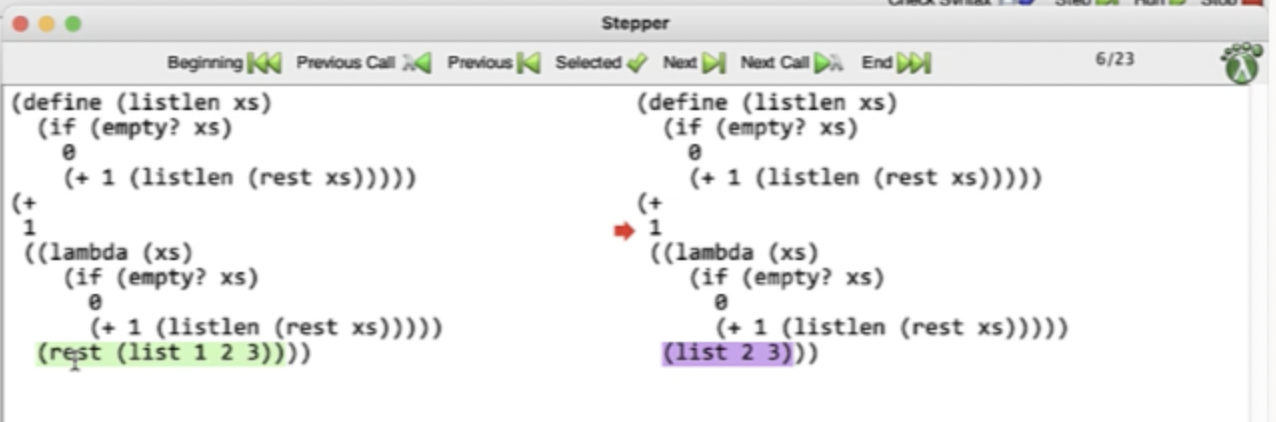
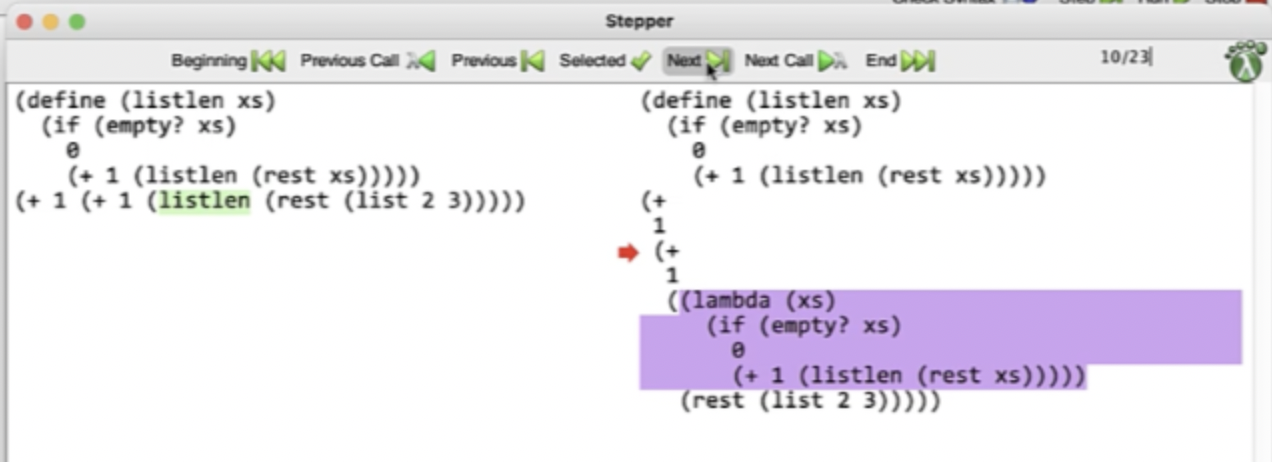
This continues on until the base case…