CS135-hw-20210203

FSM #

Alphabets: {a, b} or {0, 1}

Strings which begin and end with a different letter

#alphabet
a
b
#states
0
aa
ab
ba
bb
#initial
0
#accepting
ab
ba
#transitions
0:a>aa
0:b>bb
aa:a>aa
aa:b>ab
bb:b>bb
bb:a>ba
ab:b>ab
ab:a>aa
ba:a>ba
ba:b>bb

Strings with at least 2 occurences of ab

#alphabet
a
b
#states
0
s1
1
s2
2
#initial
0
#accepting
2
#transitions
0:a>s1
0:b>0
s1:a>s1
s1:b>1
1:a>s2
1:b>1
s2:a>s2
s2:b>2
2:a>2
2:b>2

Strings with exactly one 0 and at least one 1

#alphabet
0
1
#states
s0
onezero
oneone
good
garb
#initial
s0
#accepting
good
#transitions
s0:0>onezero
s0:1>oneone

onezero:1>good
onezero:0>garb

oneone:0>good
oneone:1>oneone

good:0>garb
good:1>good

garb:0>garb
garb:1>garb

Strings that container ab

#alphabet
a
b

#states
s0
s1
good

#initial
s0

#accepting
good

#transitions
s0:a>s1
s0:b>s0

s1:b>good
s1:a>s1

good:a>good
good:b>good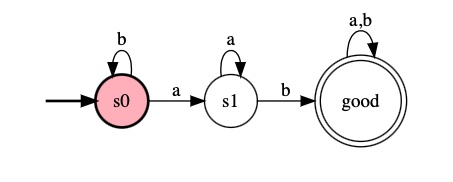

Strings that start with ab

#alphabet
a
b

#states
s0
s1
good
garb

#initial
s0

#accepting
good

#transitions
s0:a>s1
s0:b>garb

s1:a>garb
s1:b>good

good:a>good
good:b>good

garb:a>garb
garb:b>garb

Draw a deterministic FA (a DFA) using the alphabet {0,1} that recognizes all strings that either begin or end with three 0s (or both).

#alphabet
0
1

#states
s0
s1
s2
good

#initial
s0

#accepting
good

#transitions
s0:0>s1
s0:1>s0

s1:0>s2
s1:1>s0

s2:0>good
s2:1>s0

good:0>good
good:1>s0

RE #

Alphabets are {a,b} and {0,1}

Strings which begin and end with the same letter a(a+b)*a + b(a+b)*b
Strings with exactly two occurences of ab a*(abab)b* + a*(abab)b* + b*(abab)a* + b*(abab)b* (a* + b*)(abab)(a* + b*)
Strings with at most two occurences of ab ``