Announcements #

No graphing exercises on upcoming test despite containing some kinematics.

Today #

Clicker questions #

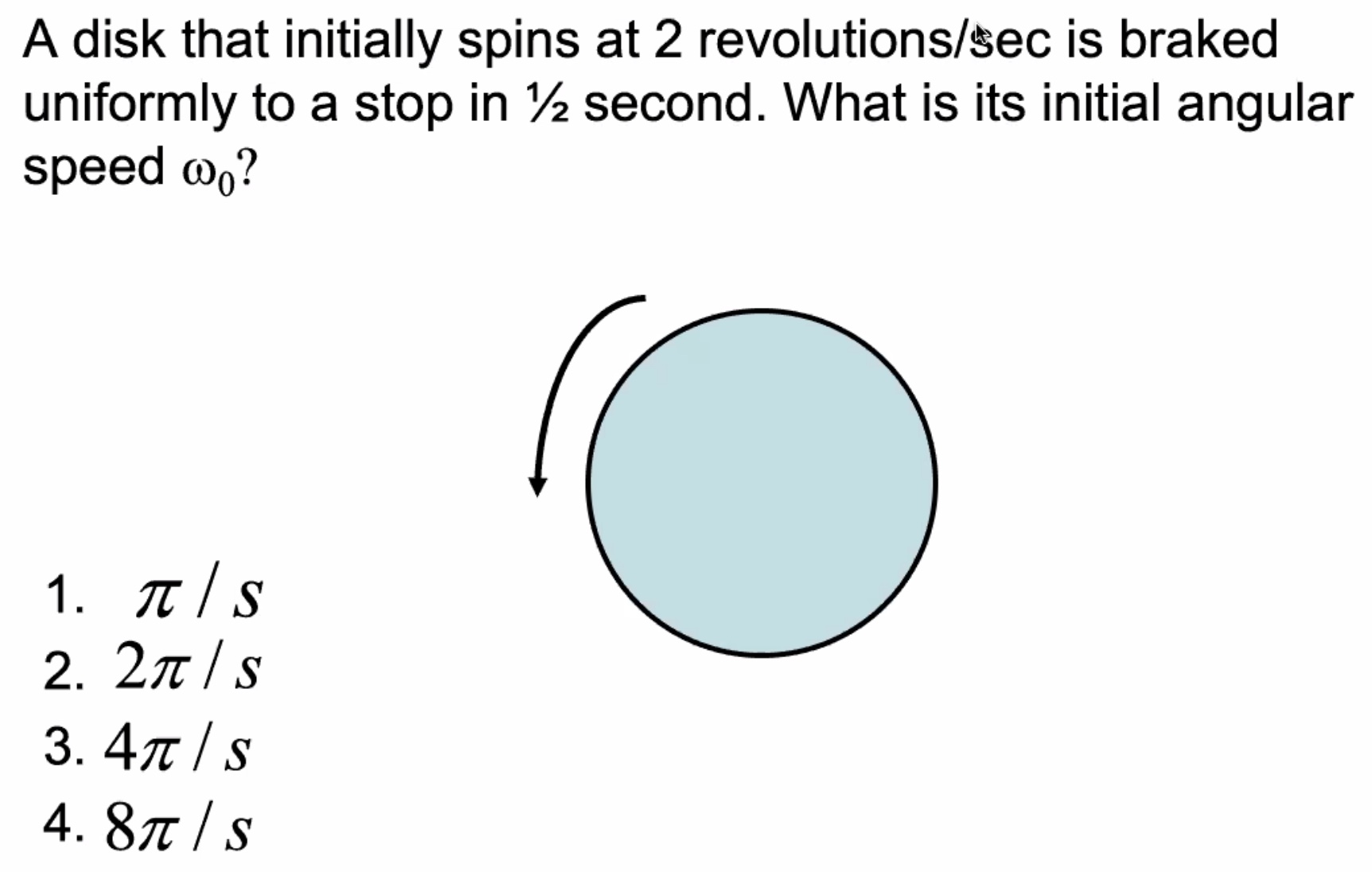
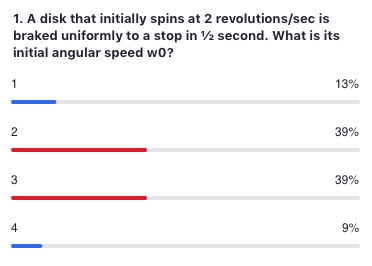
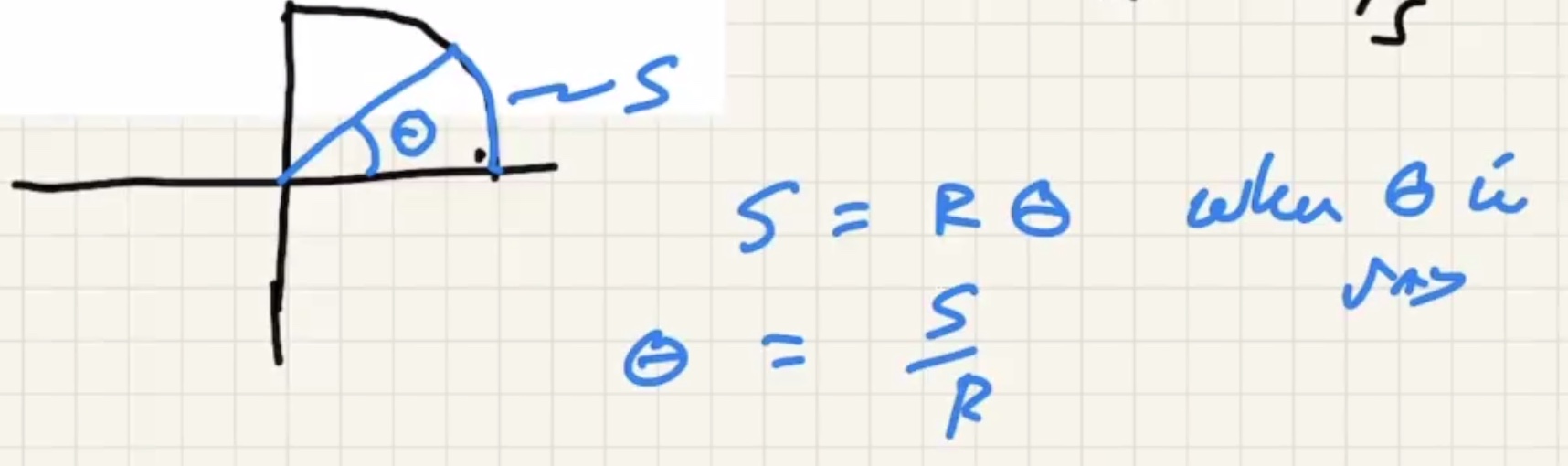
Radians are unitless. The 1/2 second doesn’t have anything to do with the problem.

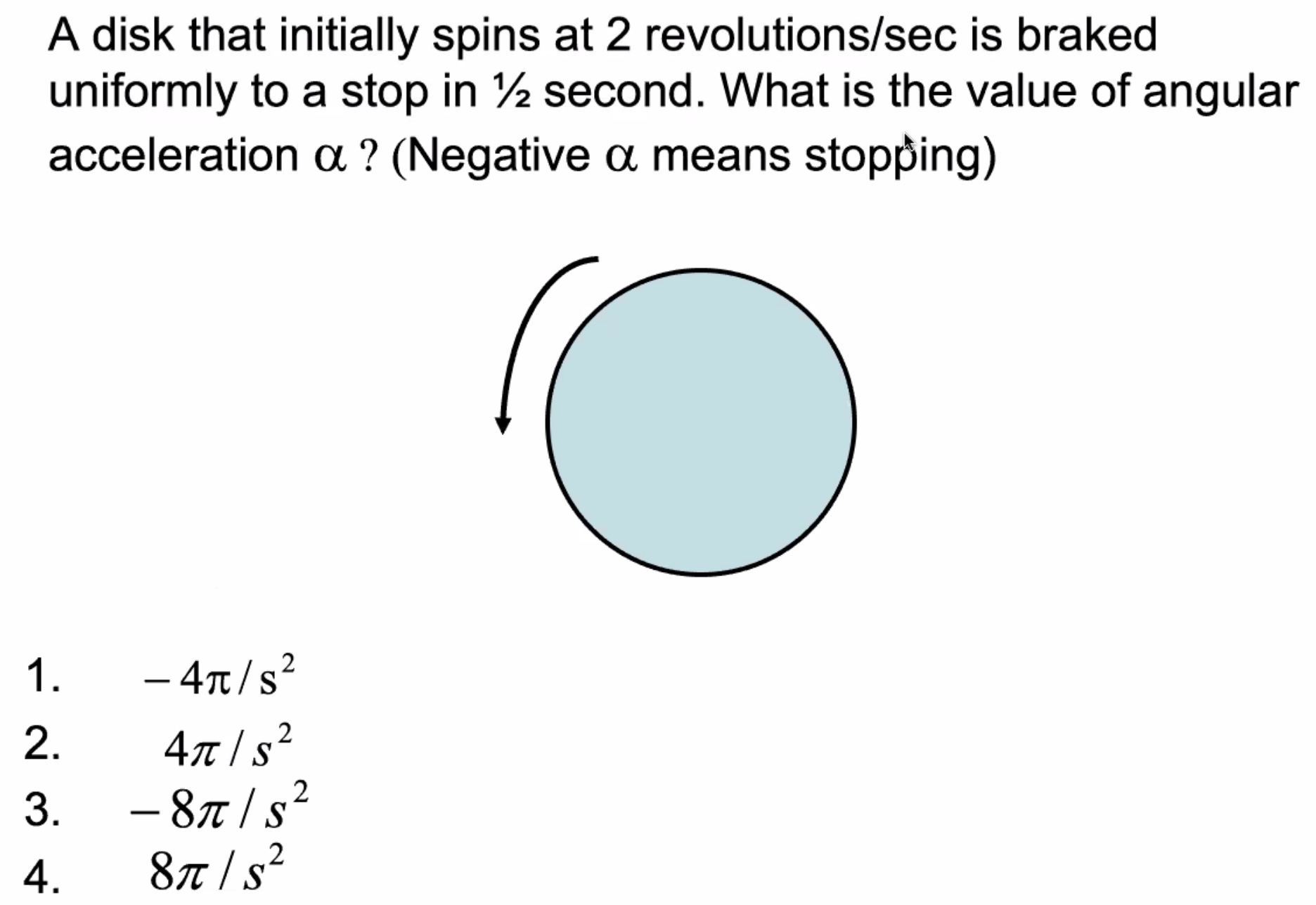
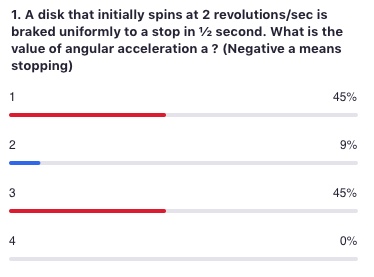
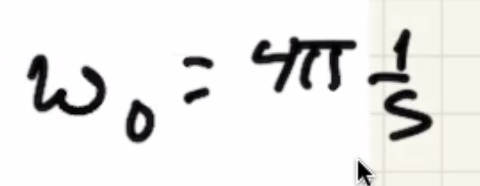
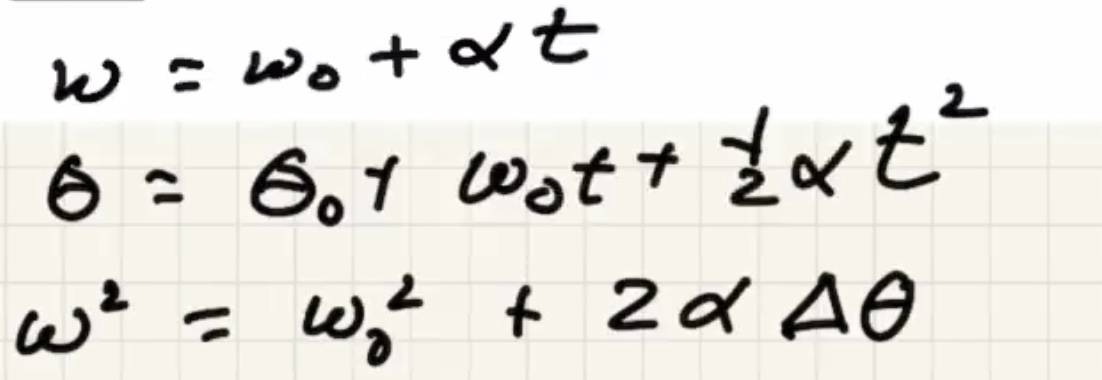
Use the first equation

You can also use this equation:

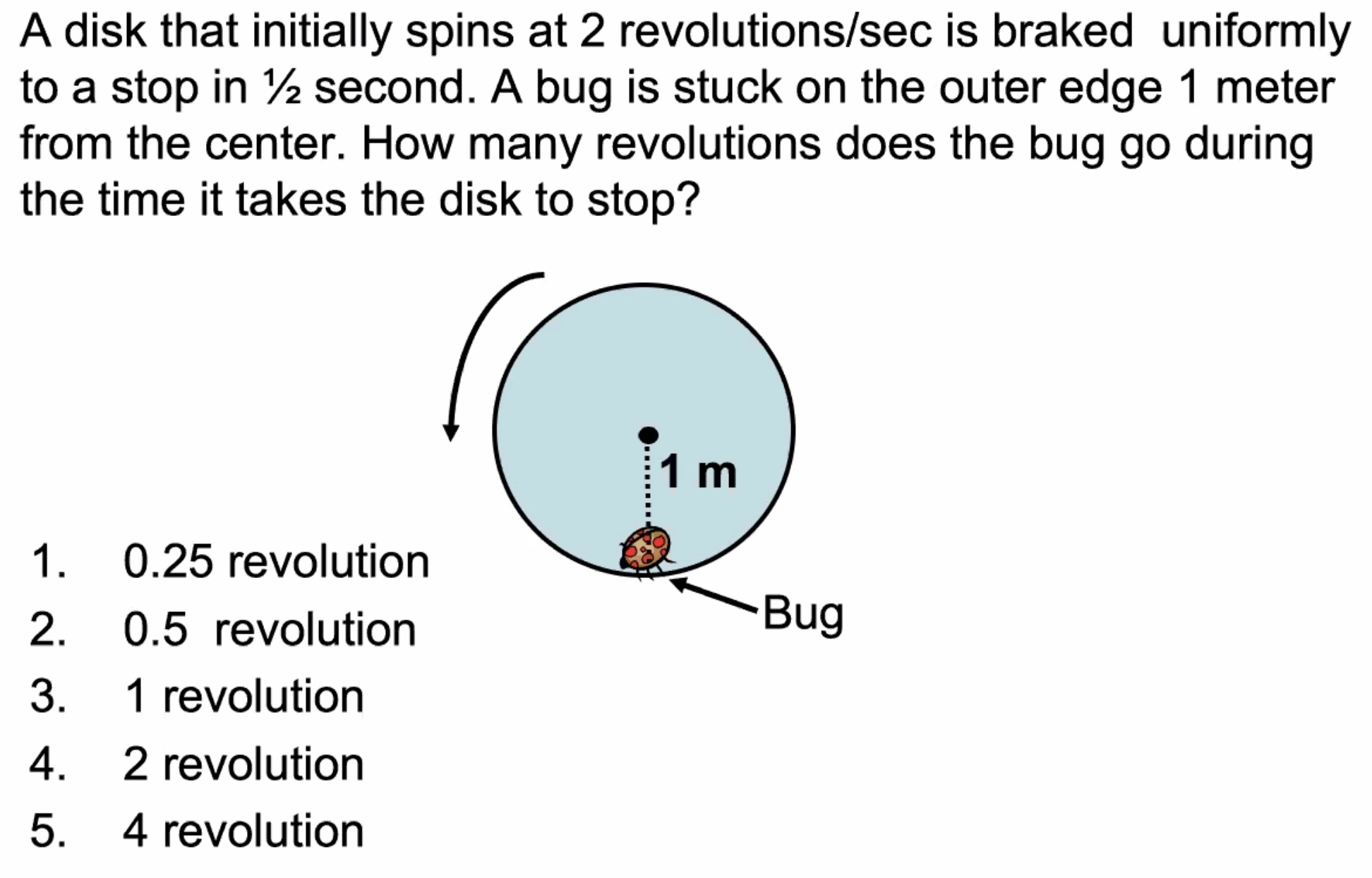
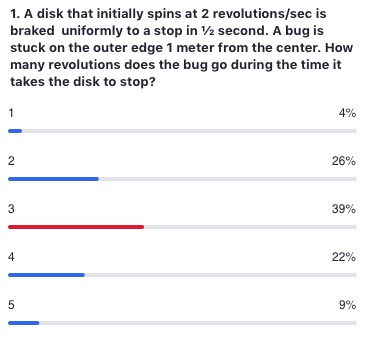
Use the third equation from above

What is the initial tangential speed $v_{oT}$ and the tangential acceleration $a_T$?

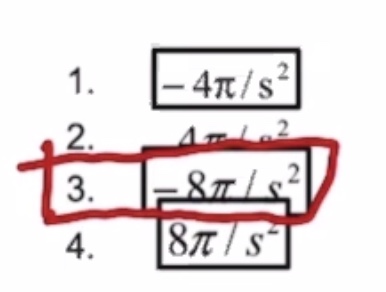
Its slowing down quite fast!

Discussion #

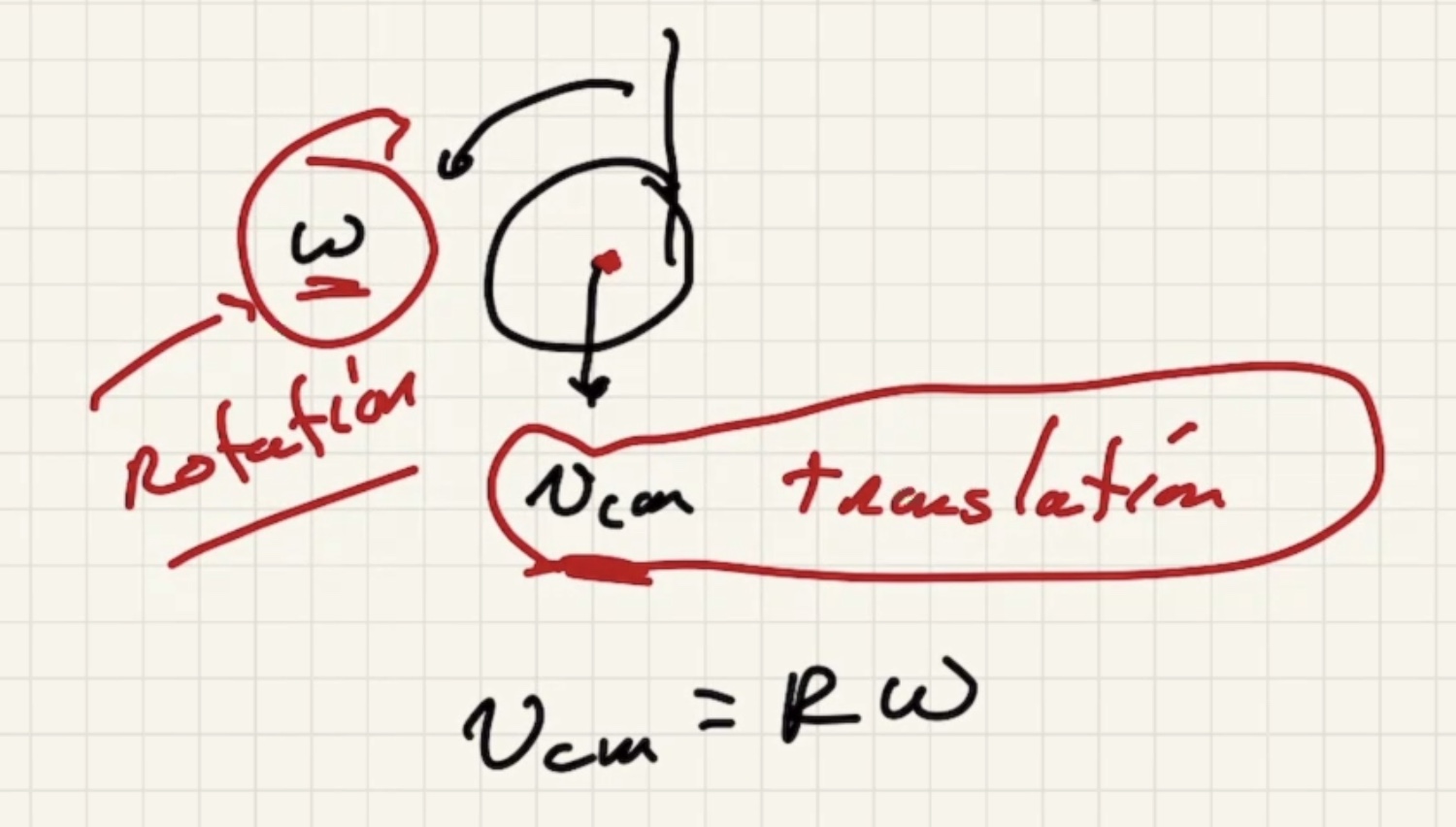
1:1 correspondence between transational motion and rotational motion.

Should be added to the list:

These link rotational motion to tangential motion. The sum of the torques is the same as sum of the forces.

Also adding in our understanding of energy:

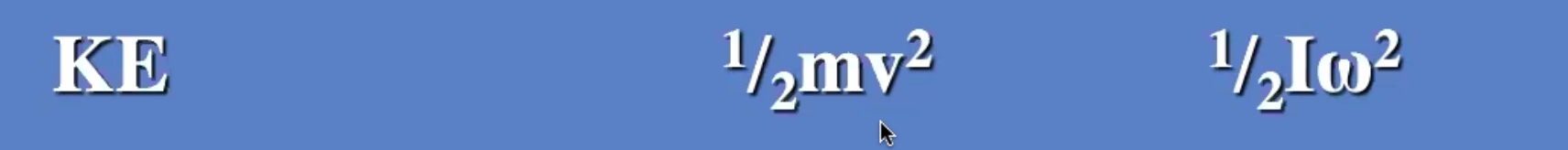
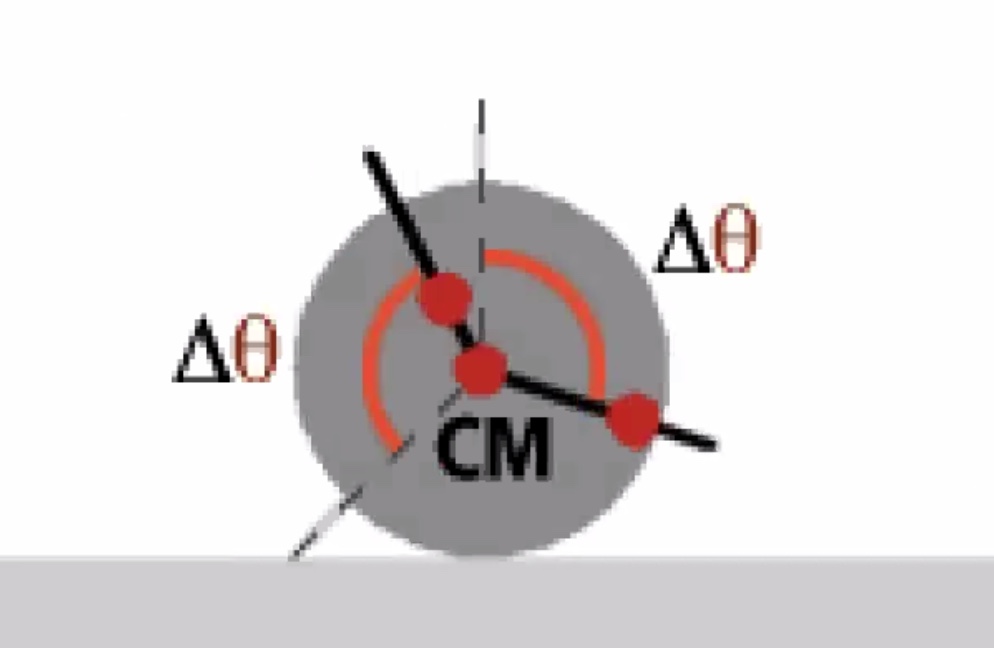
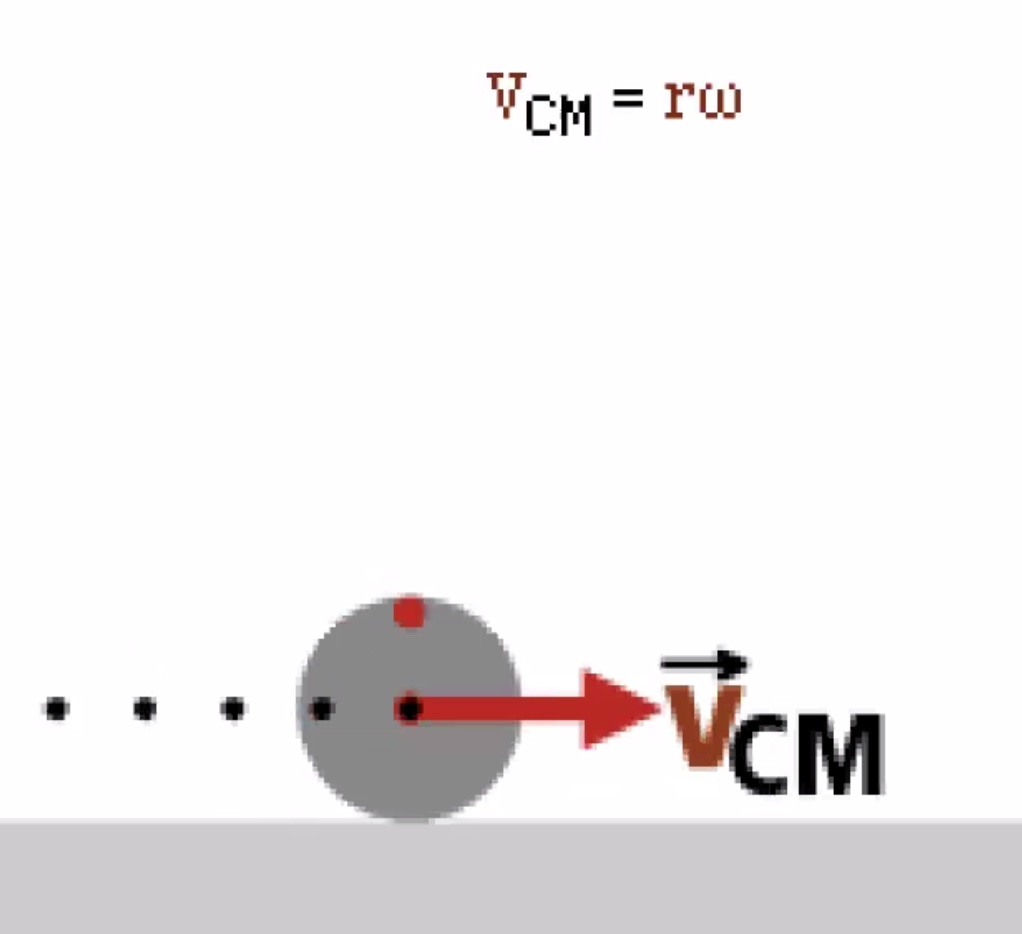
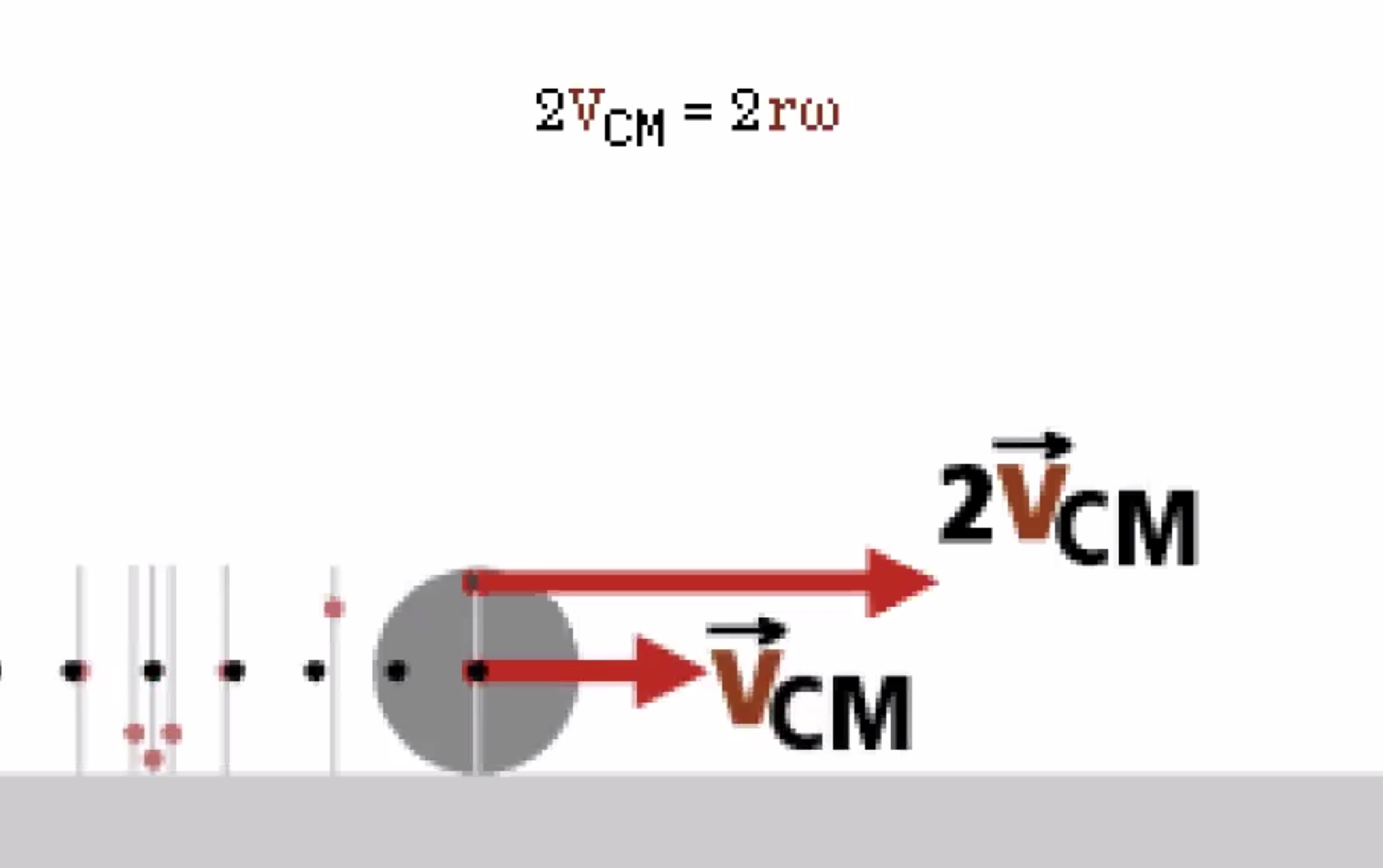
The point thats in contact with the surface is instantanteously at rest

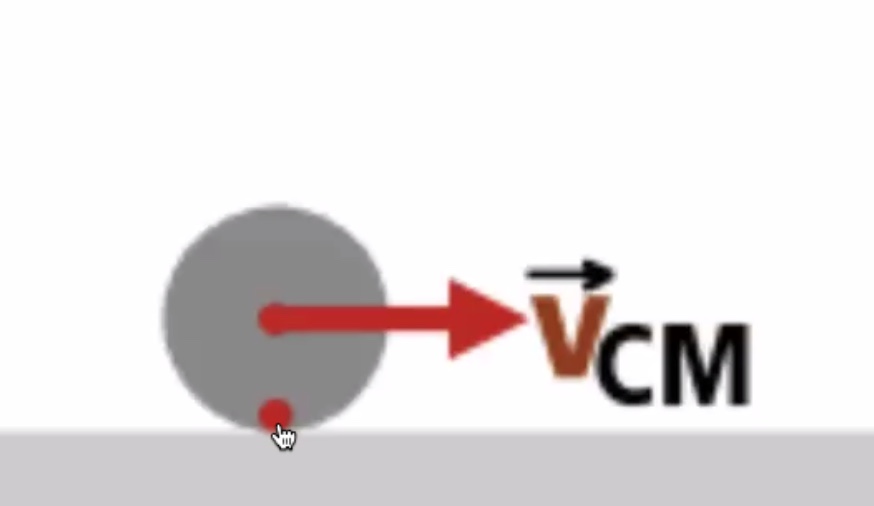
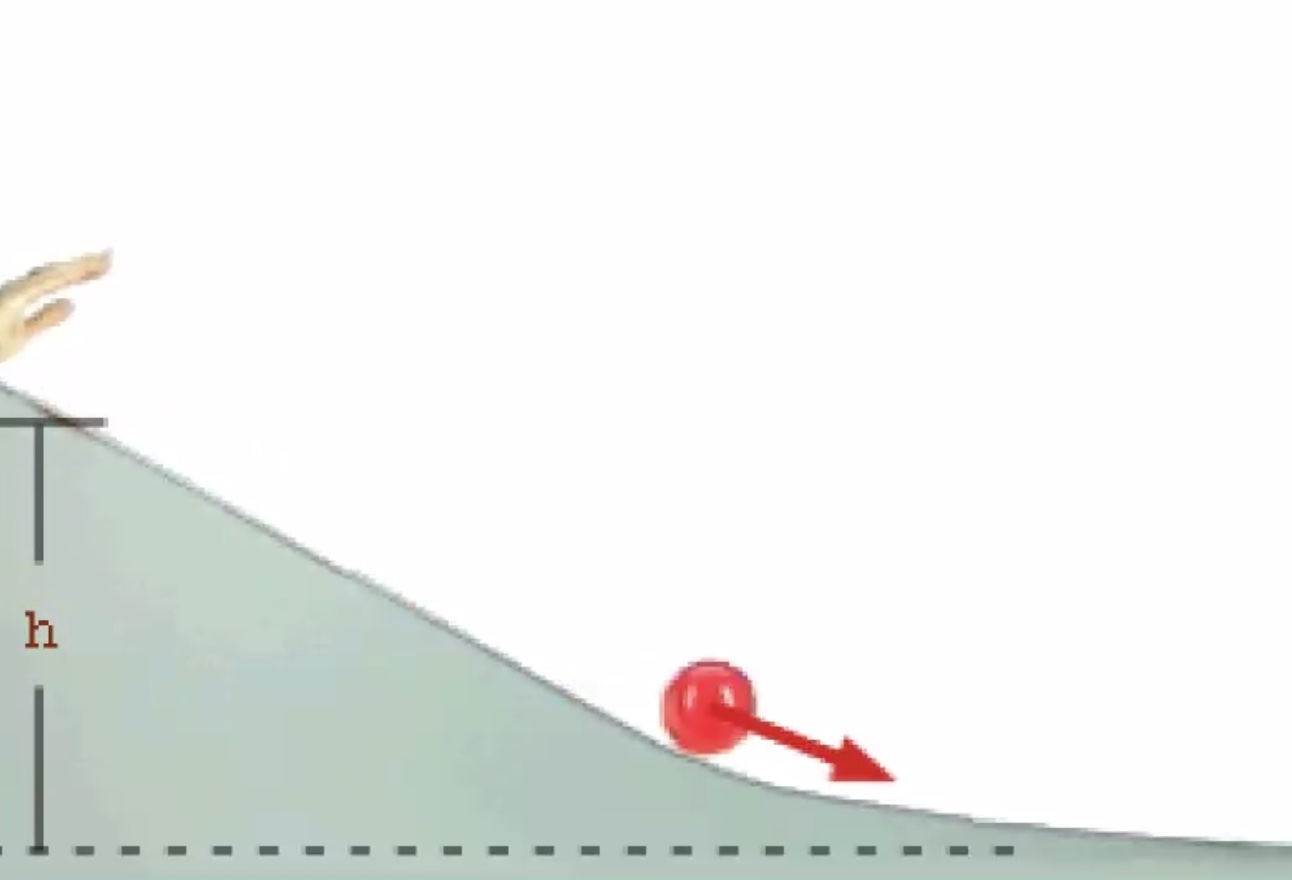
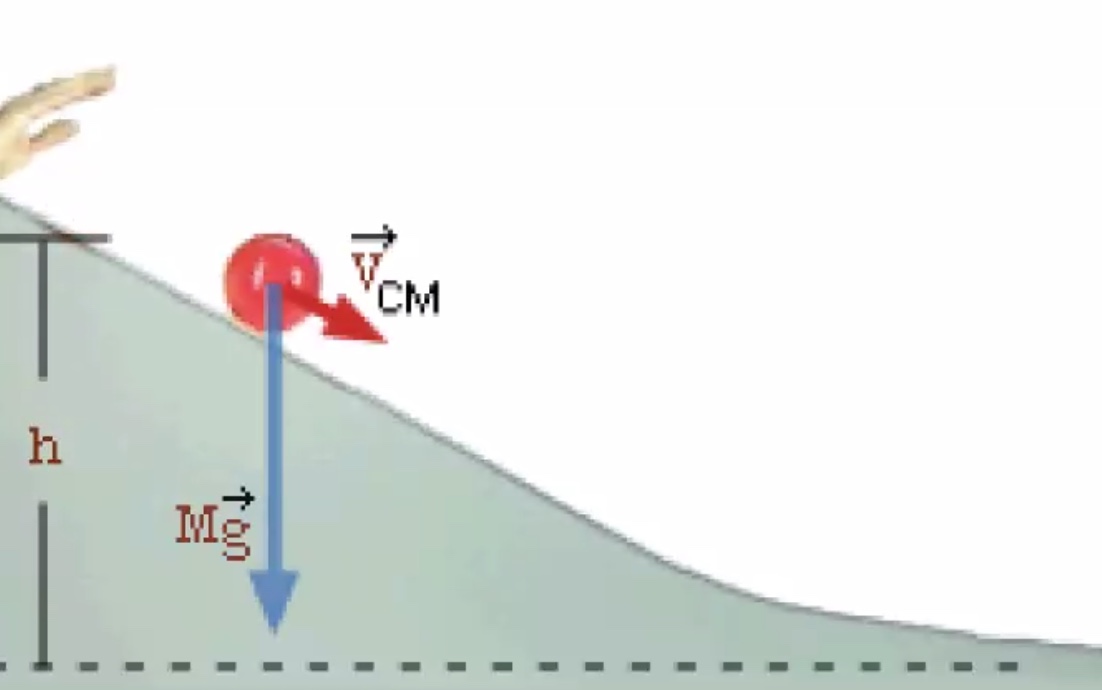
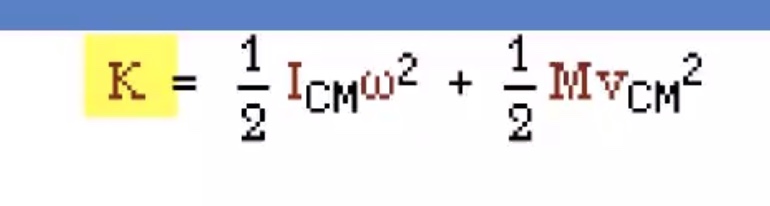
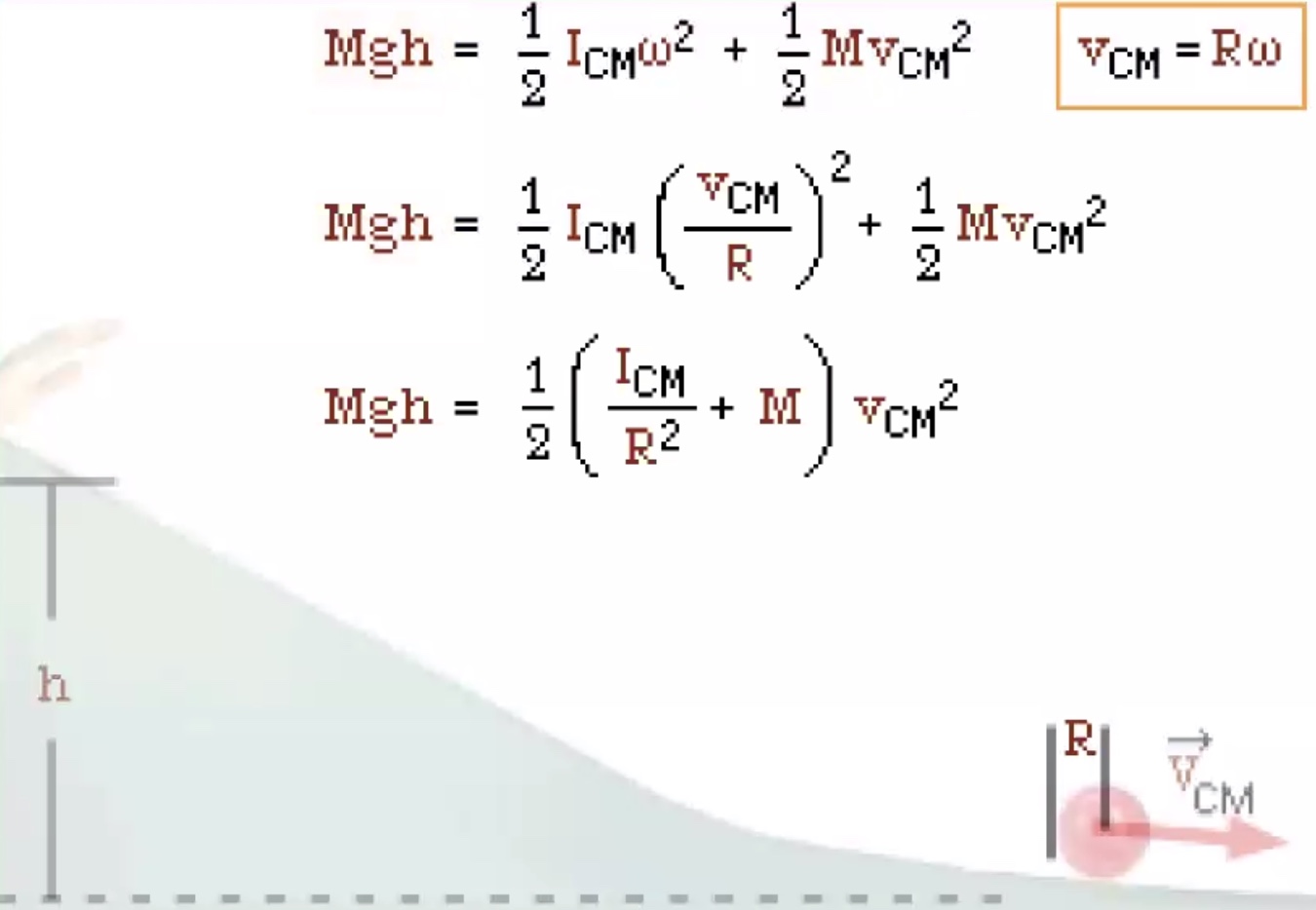
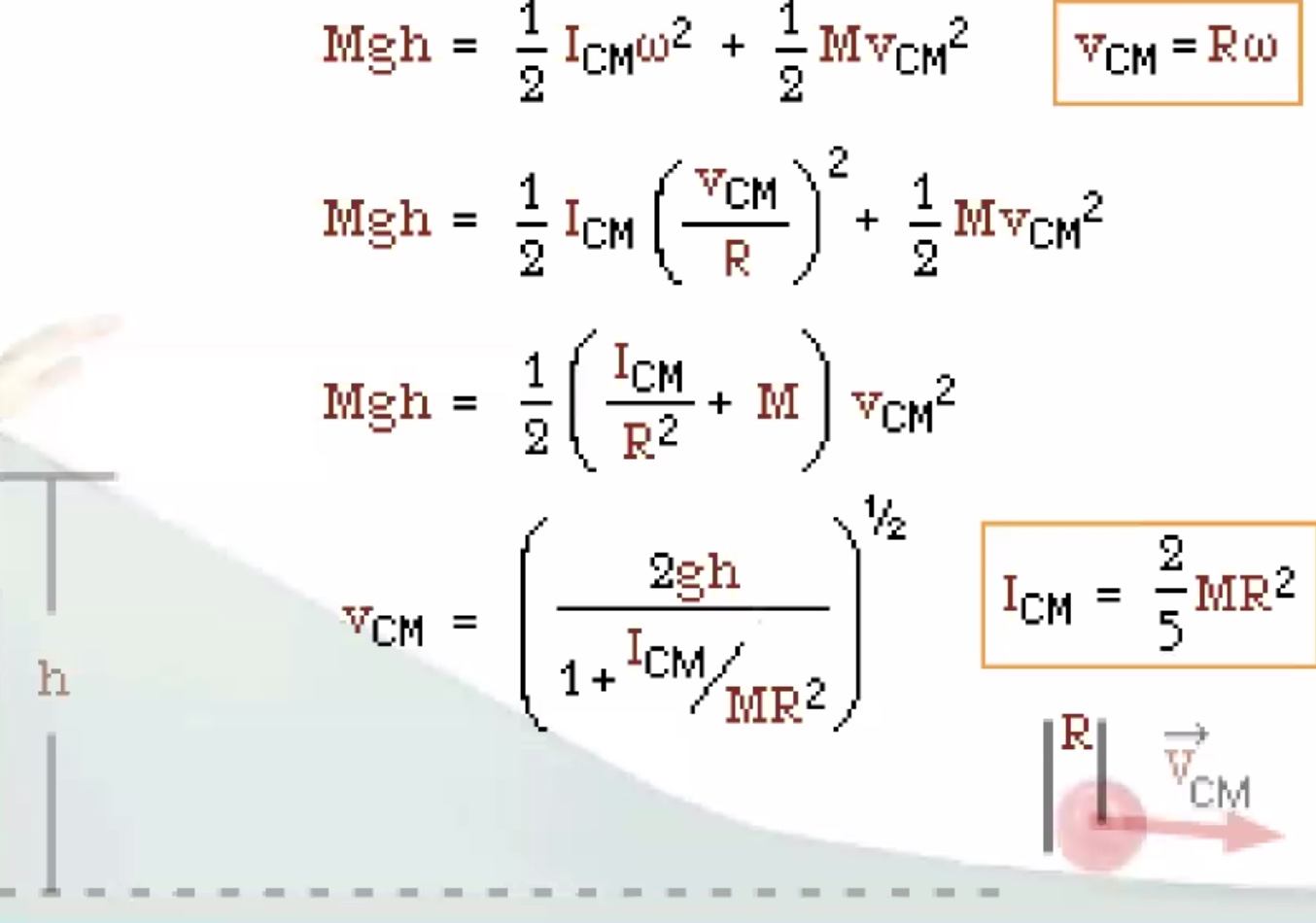
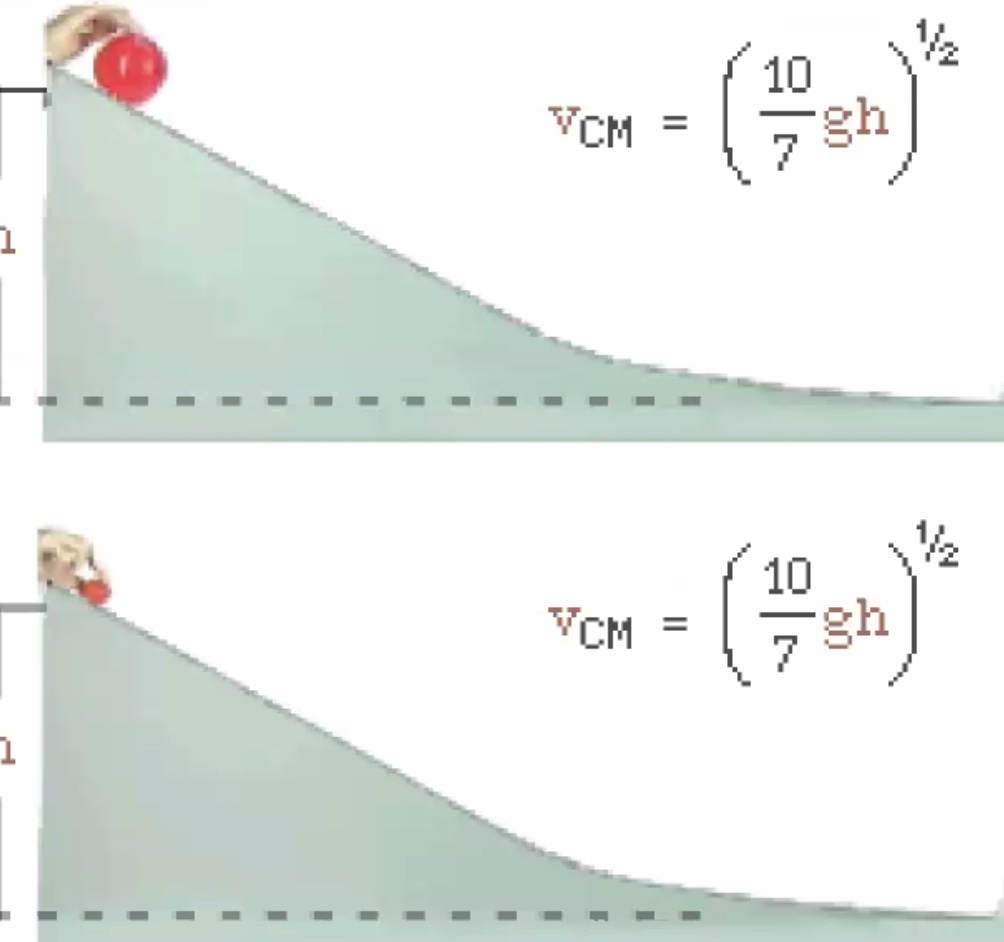
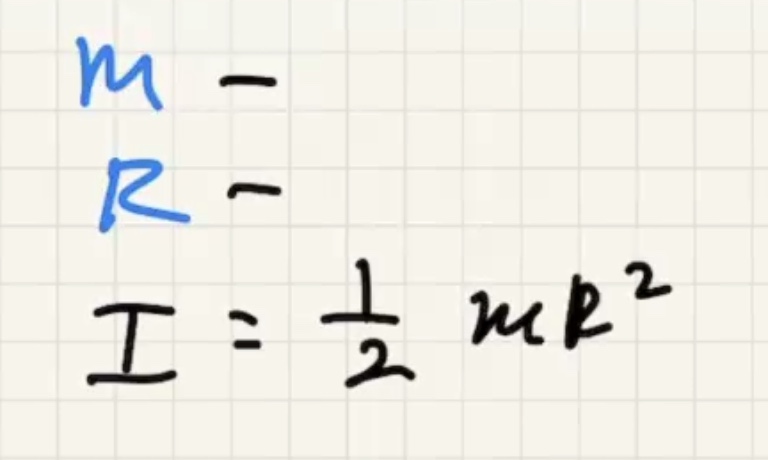
We gave two terms that go into the kinetic energy portion of the equation, how fast the center of mass is moving and how fast it is rotating about the center of mass.

Replace $\omega$

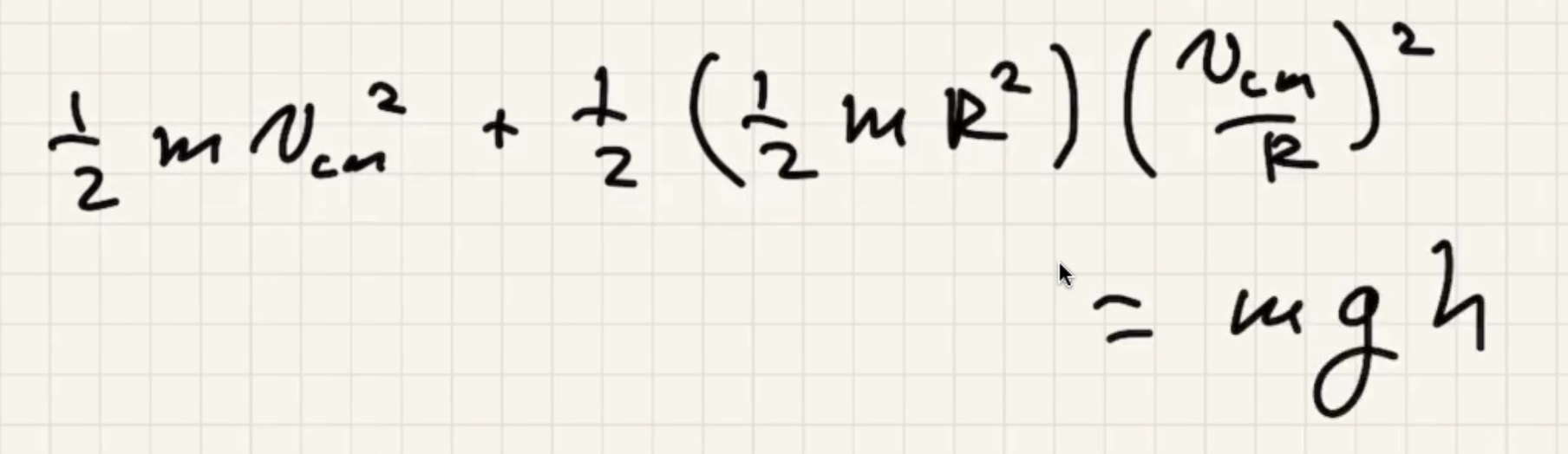
Mass $m$ is cancelled

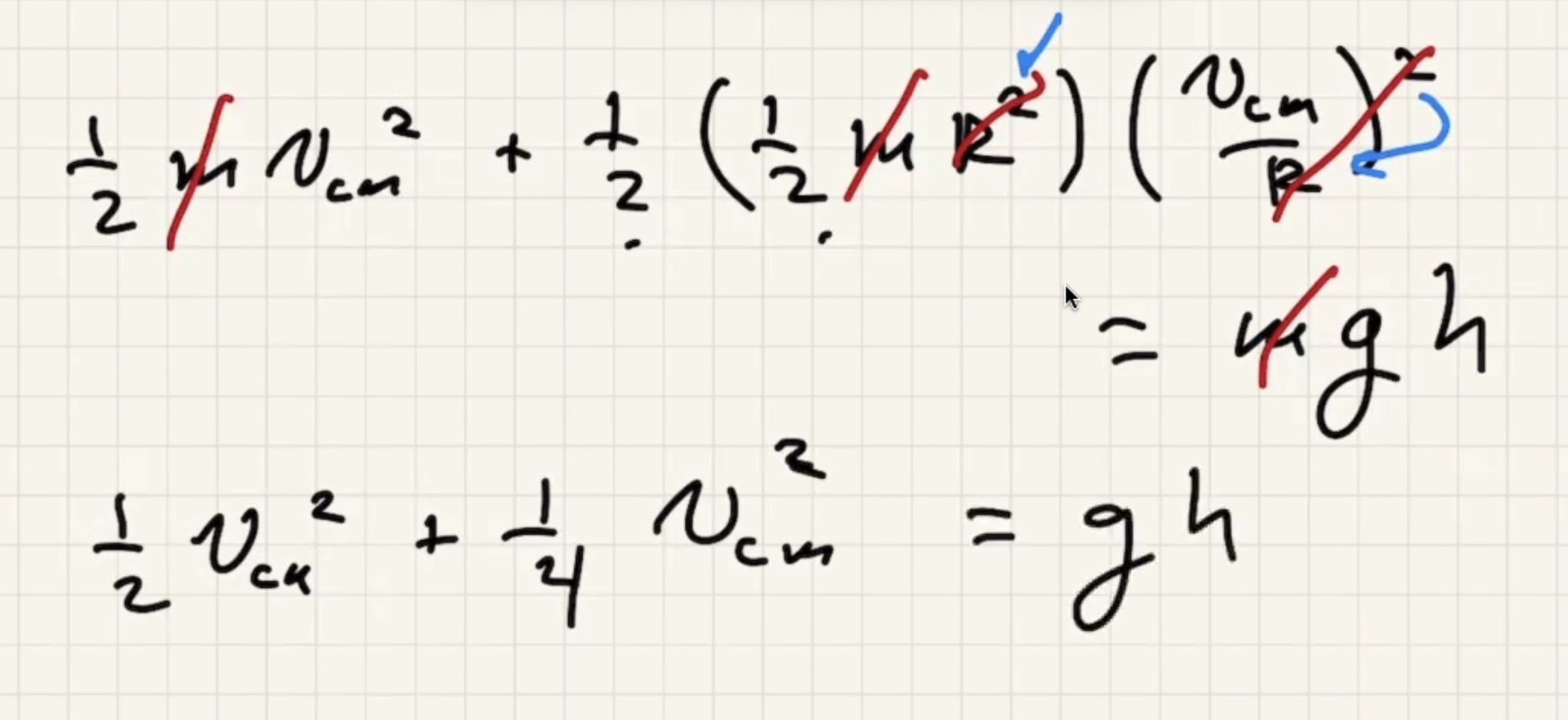
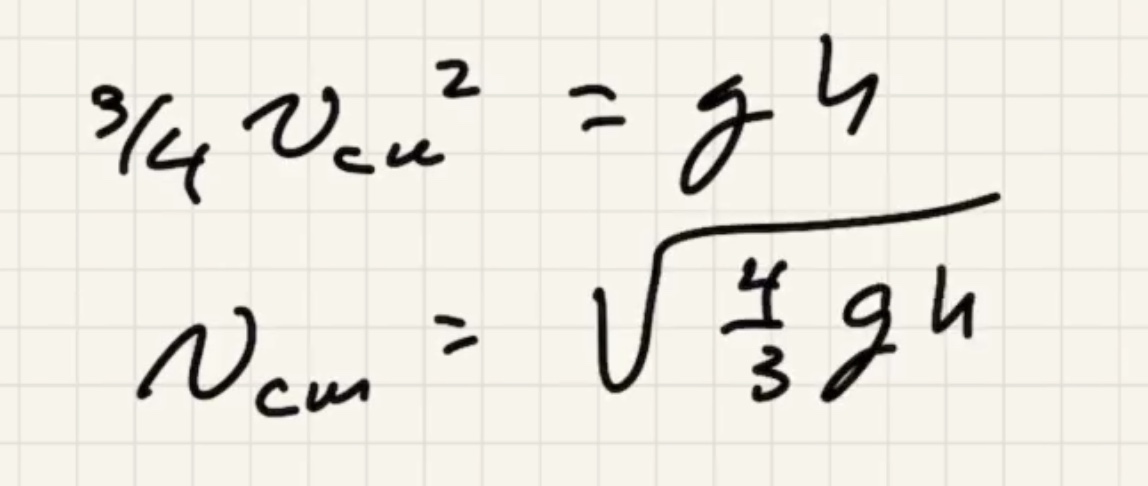
If this was just sliding (no friction) the $v_{cm}$ would be higher.

A look at the cylinder half way down the incline:

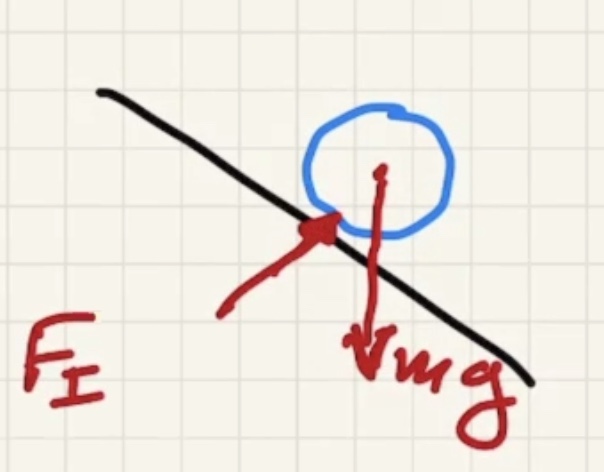
Plus a frictional force $f_s$ that creates the rotation

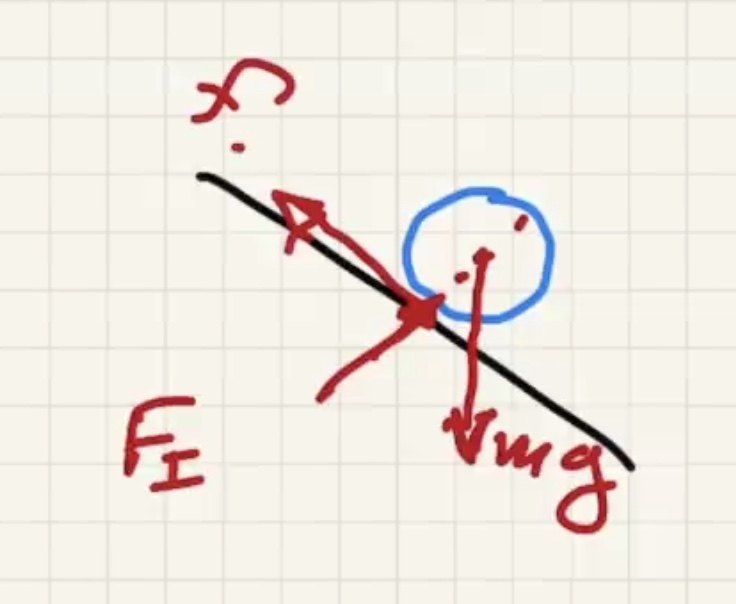
The point that is in contact is at rest so there isn’t any displace, thus no work.

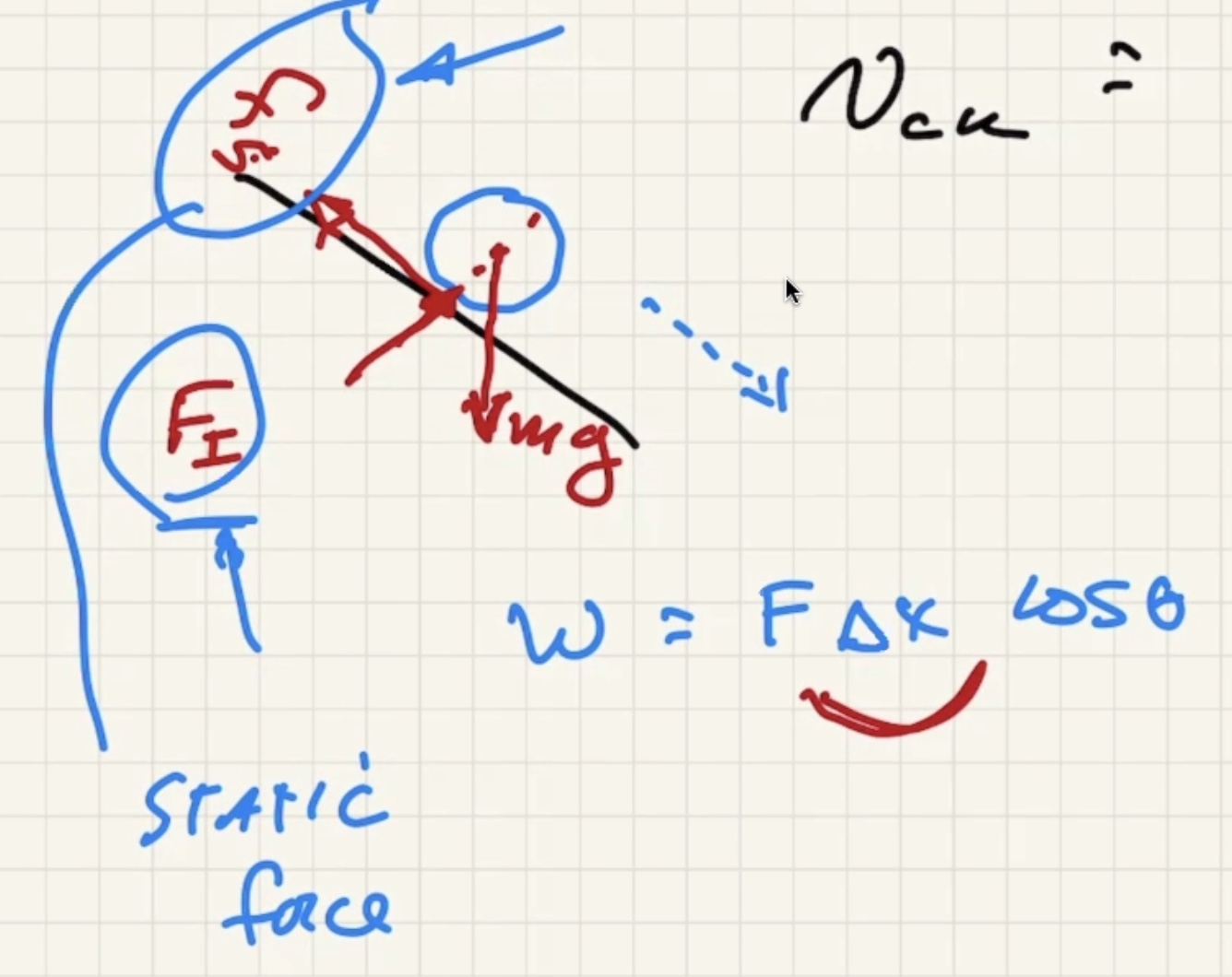
Last thing to add to the table of rotational quantities

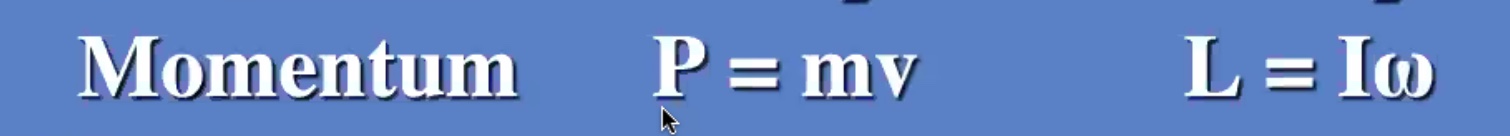
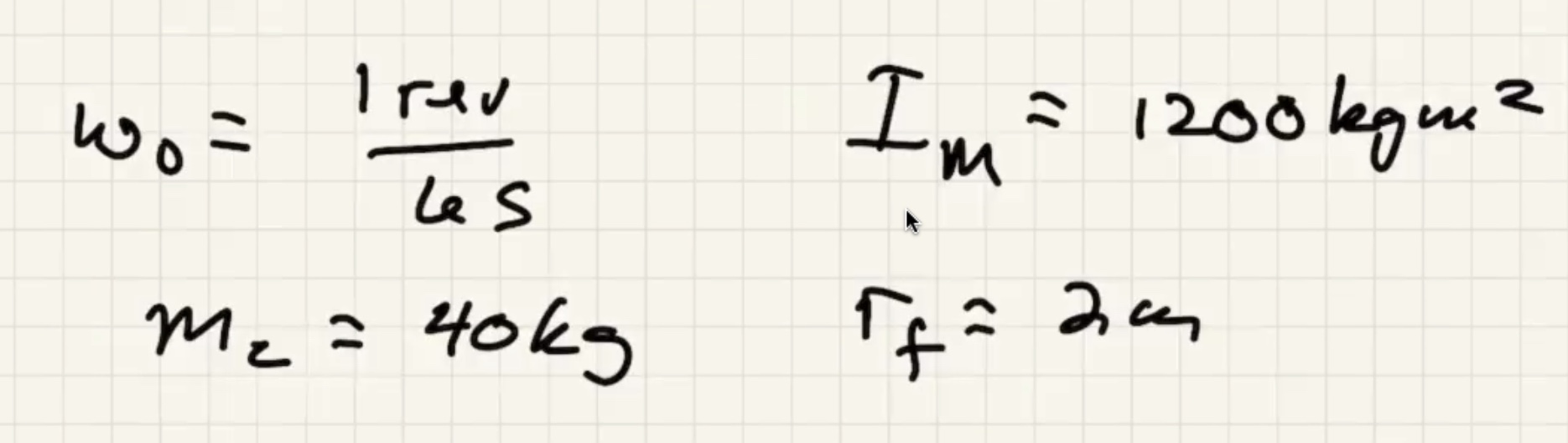
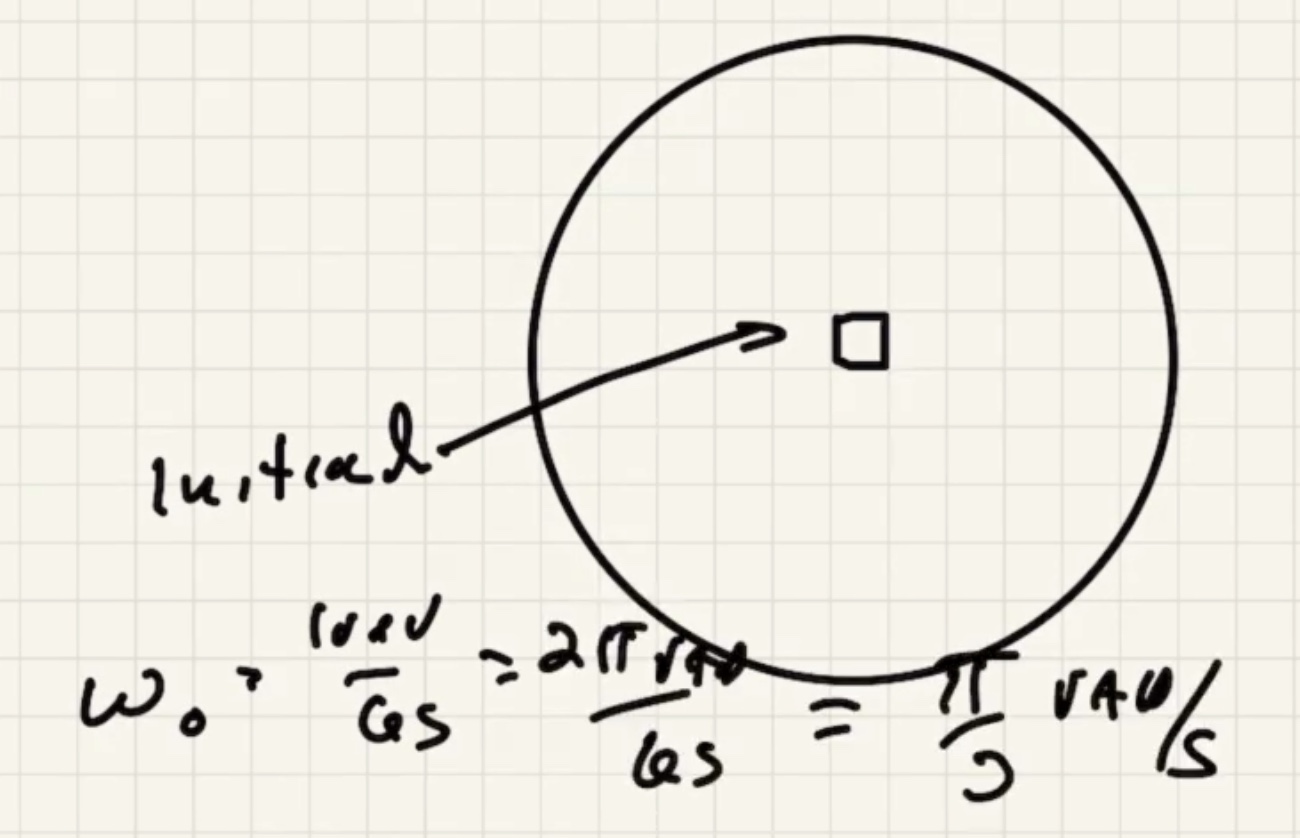
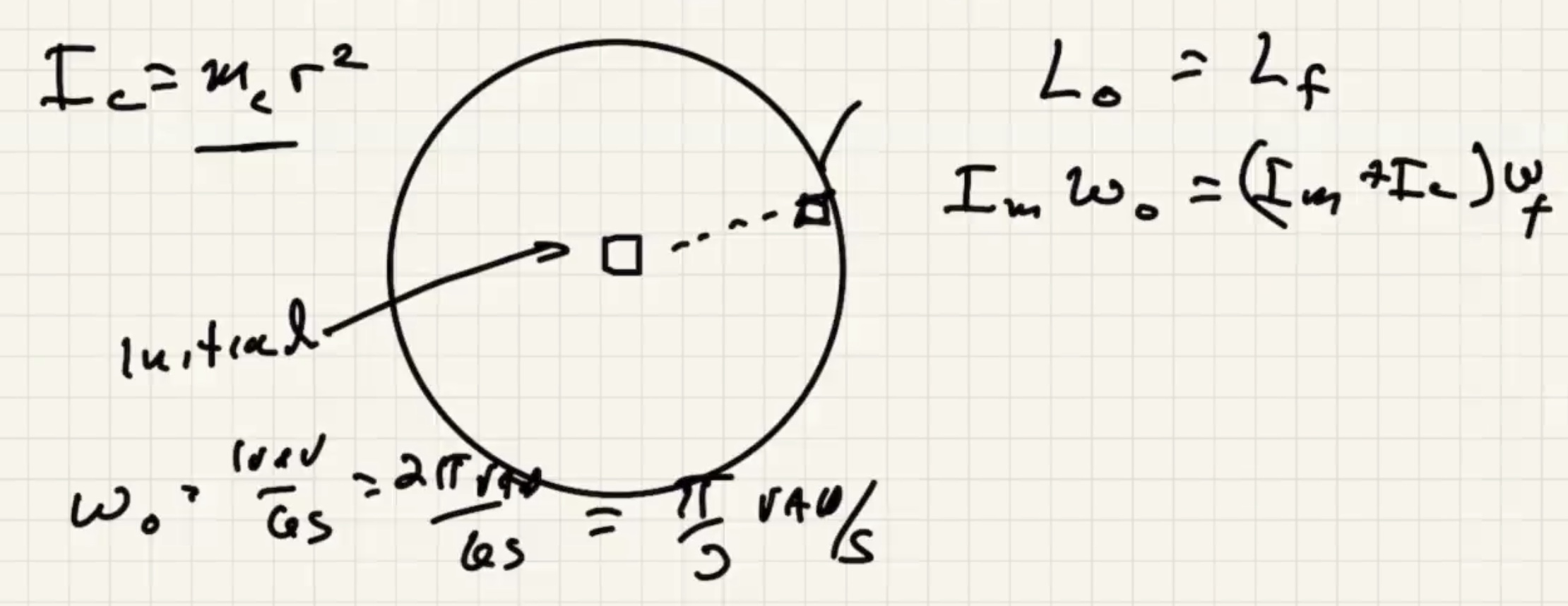
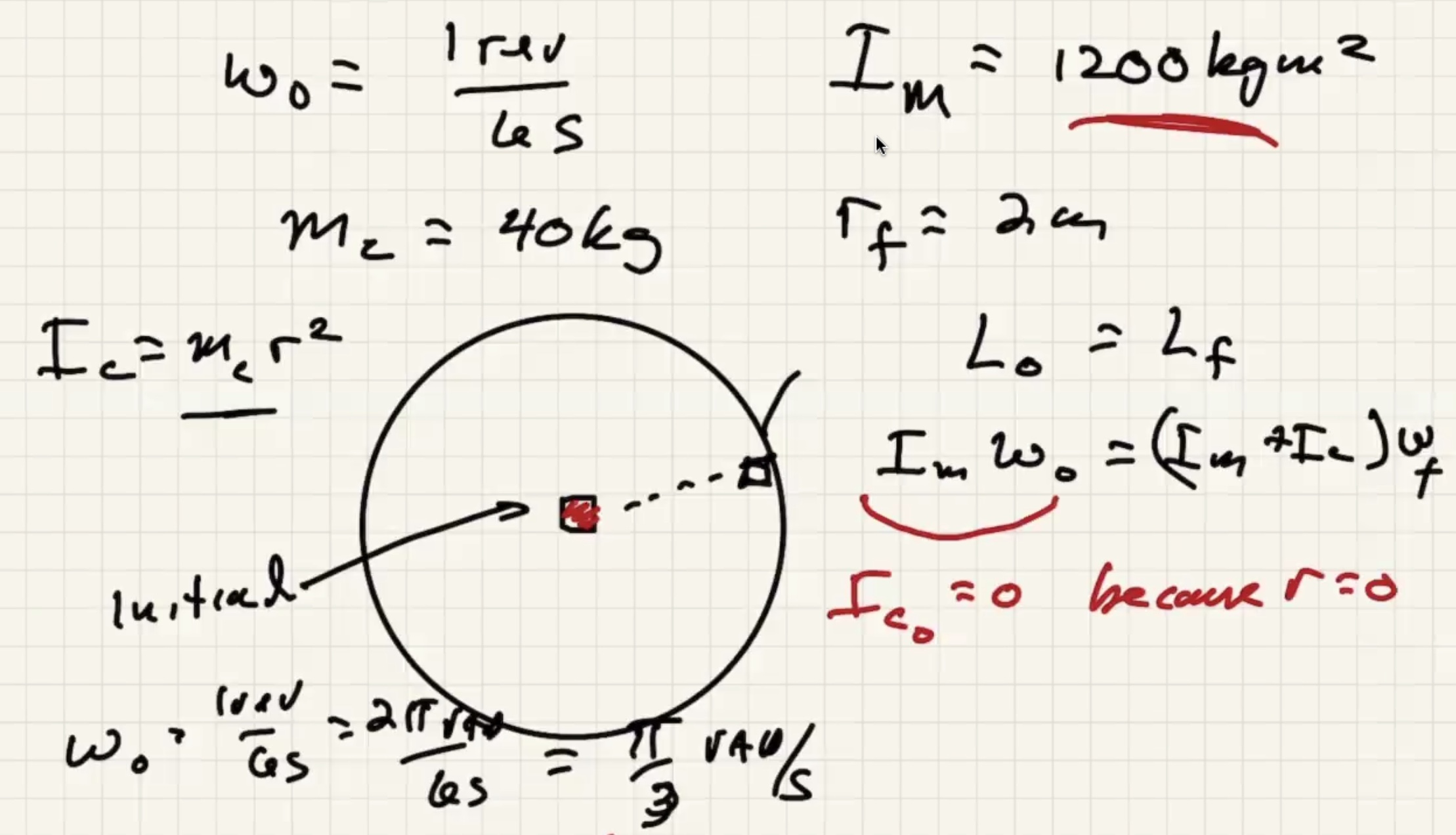
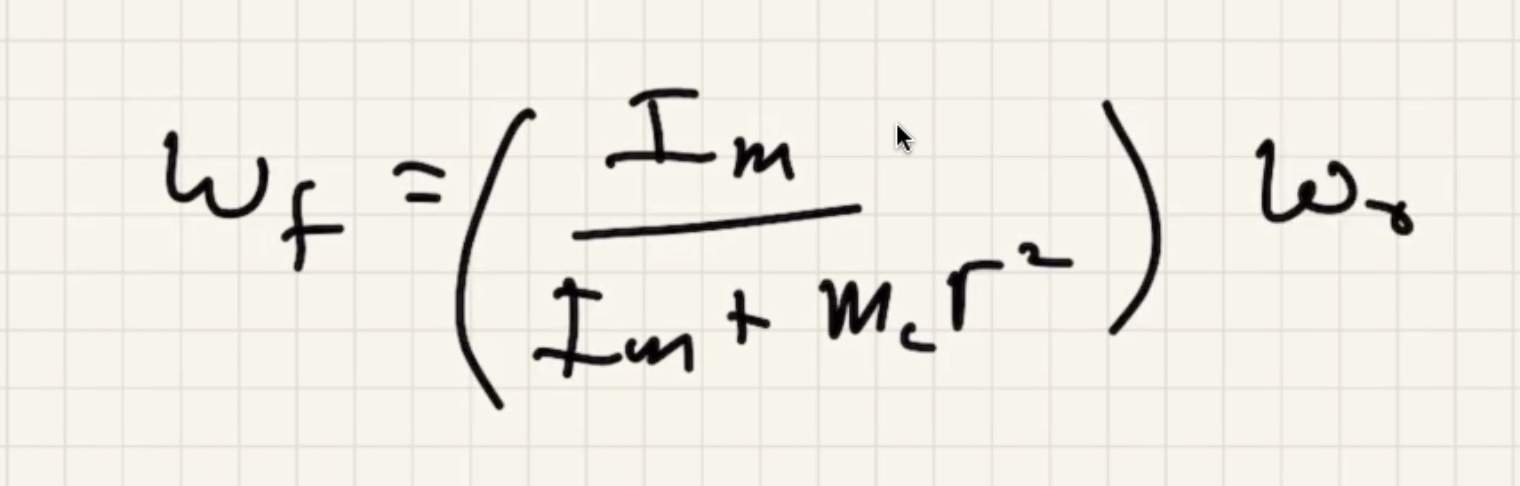
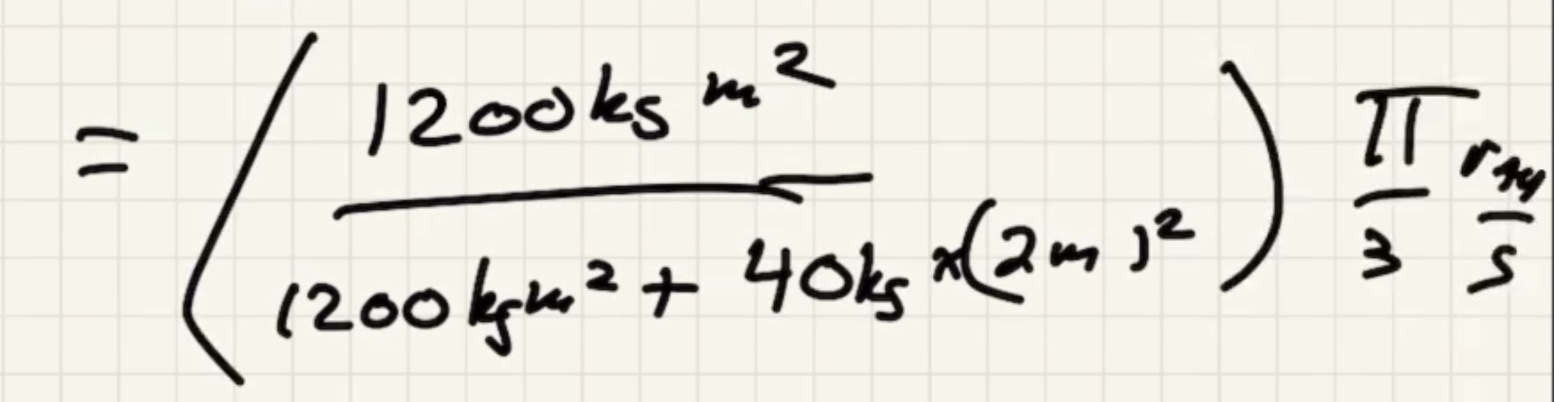
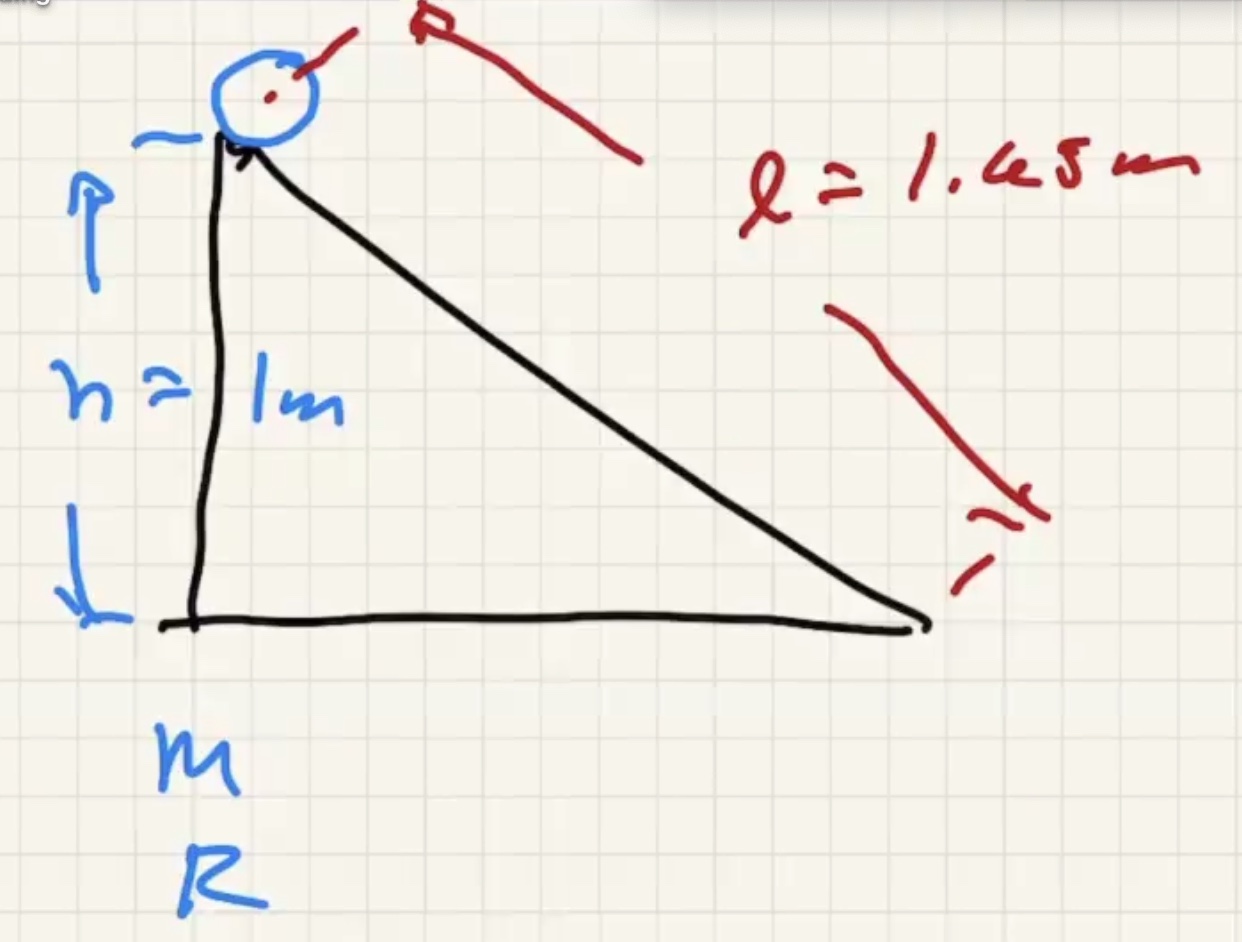
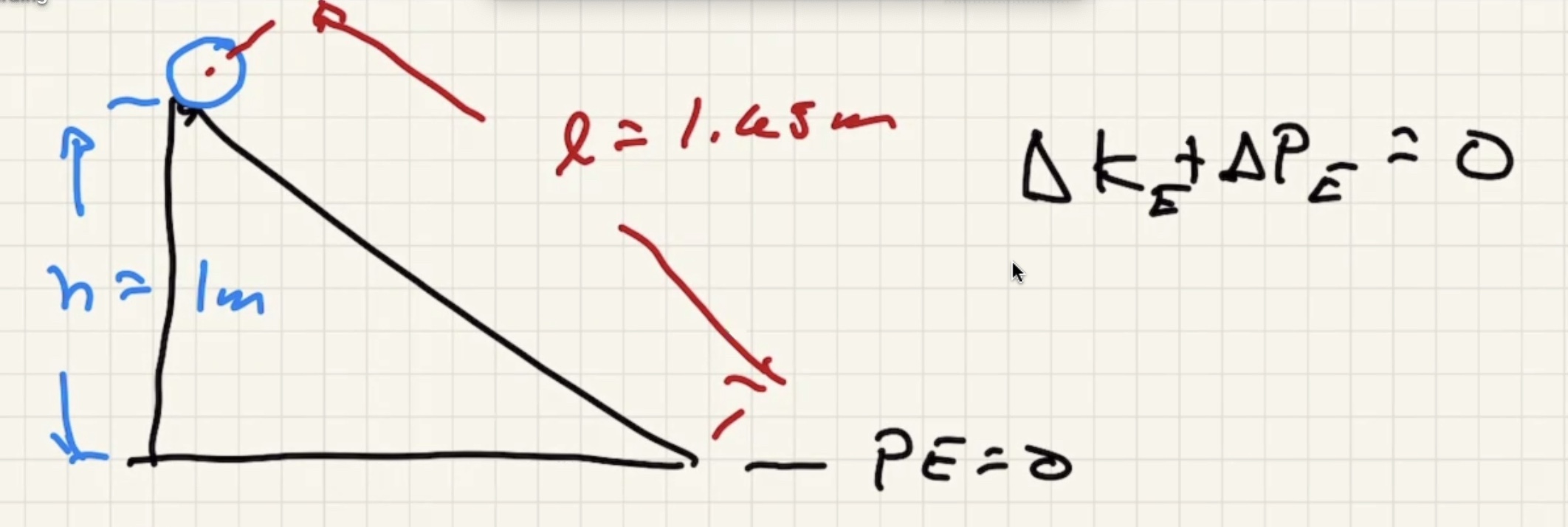
A look at Quiz 8 #

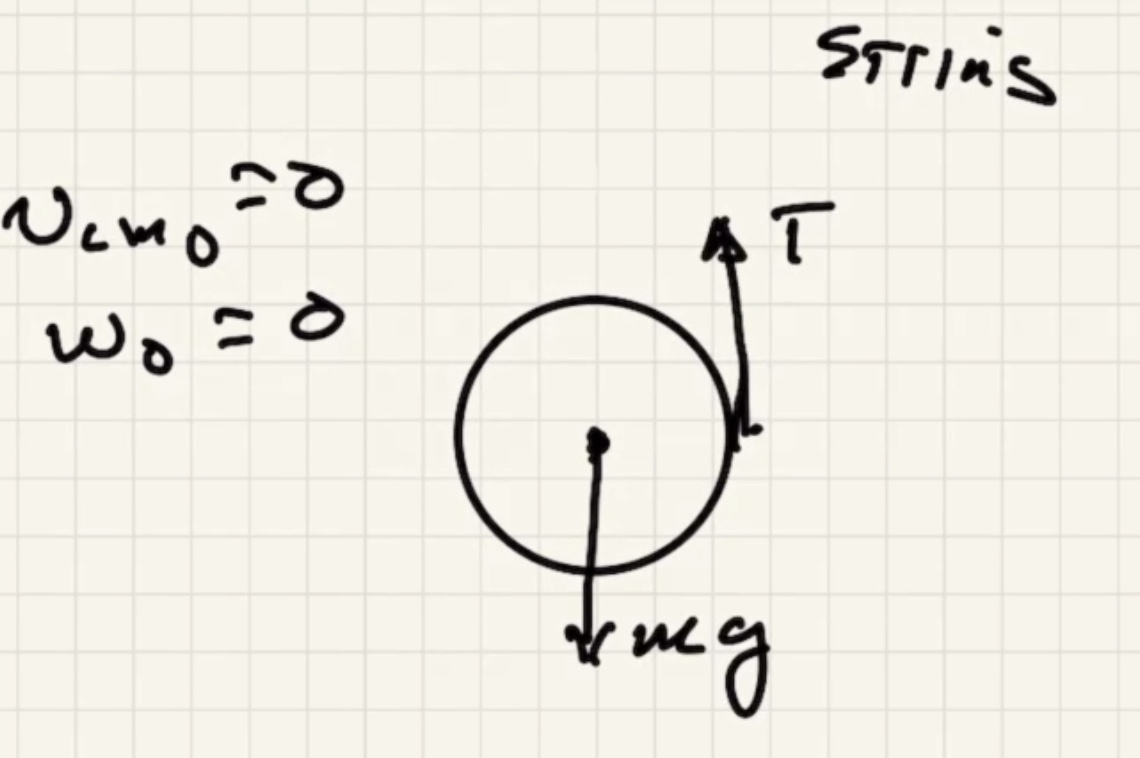
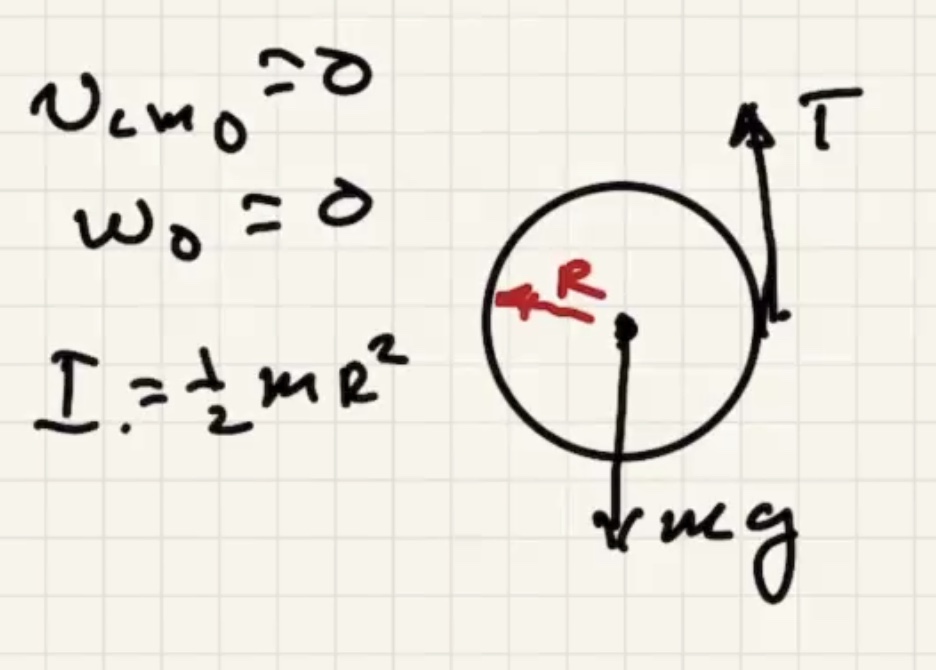
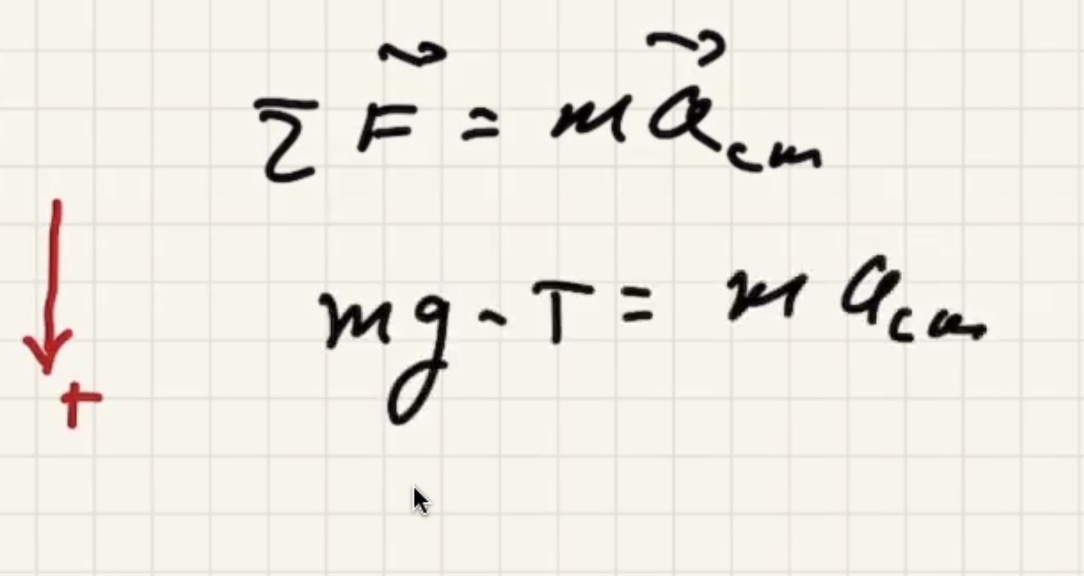
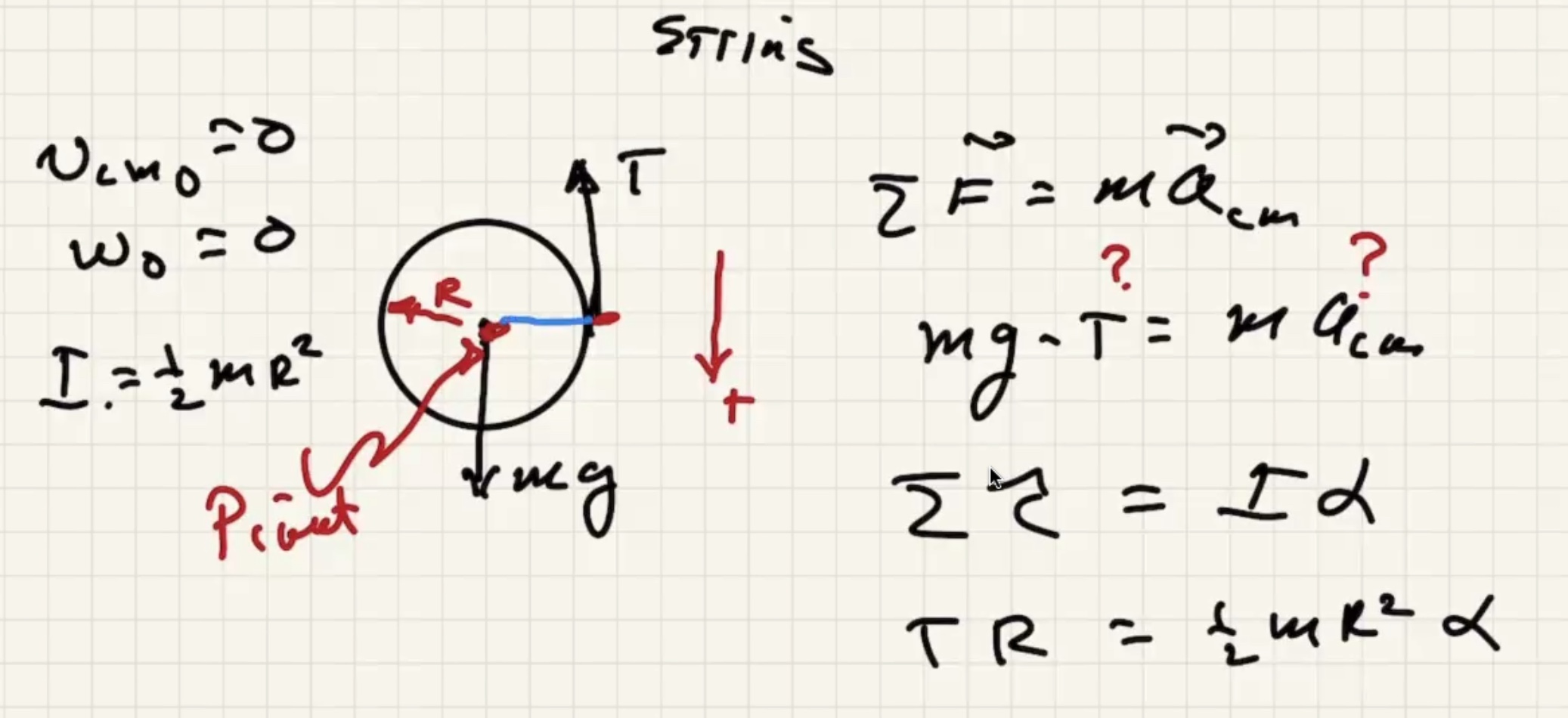
The angle is 90 degrees between pivot and moment arm.

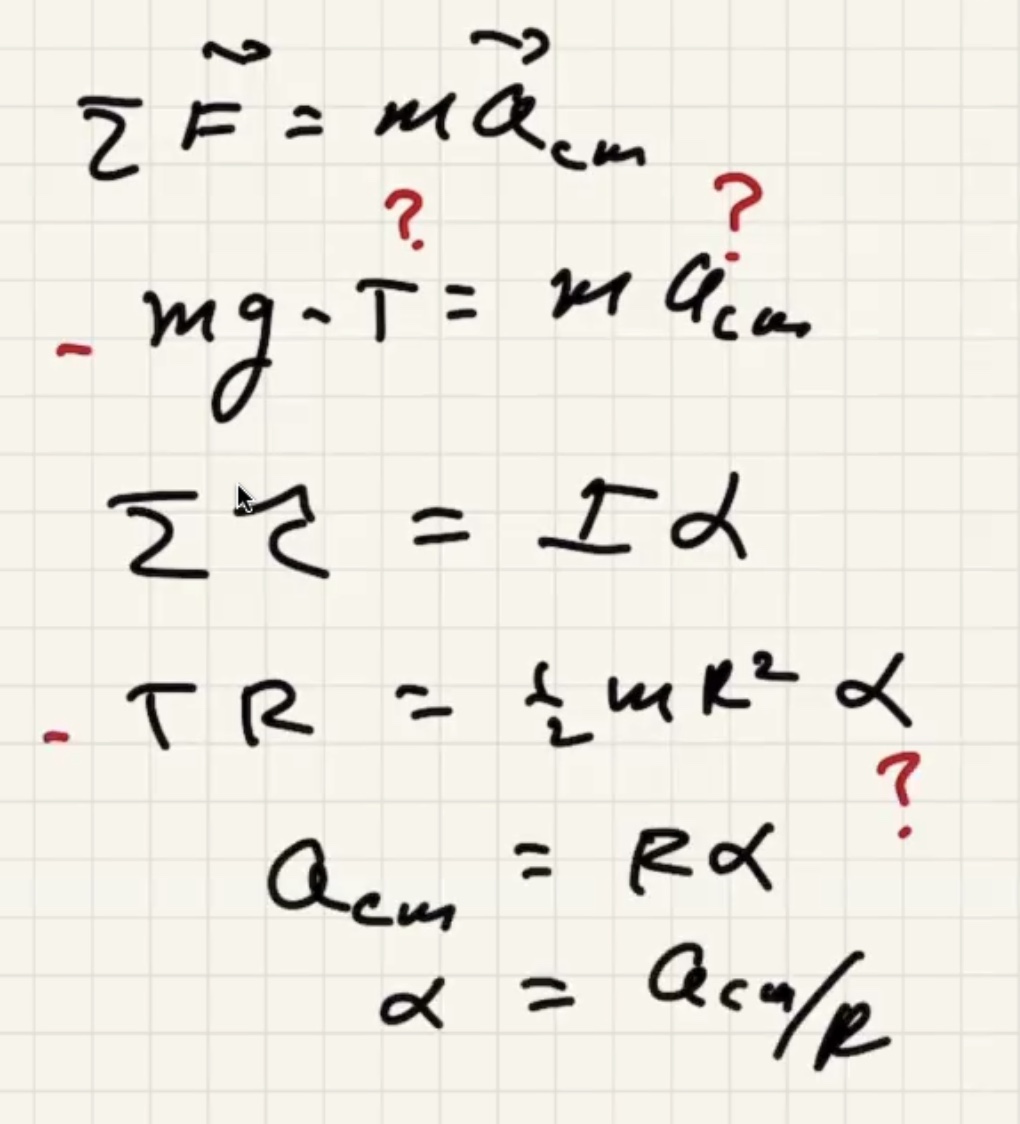
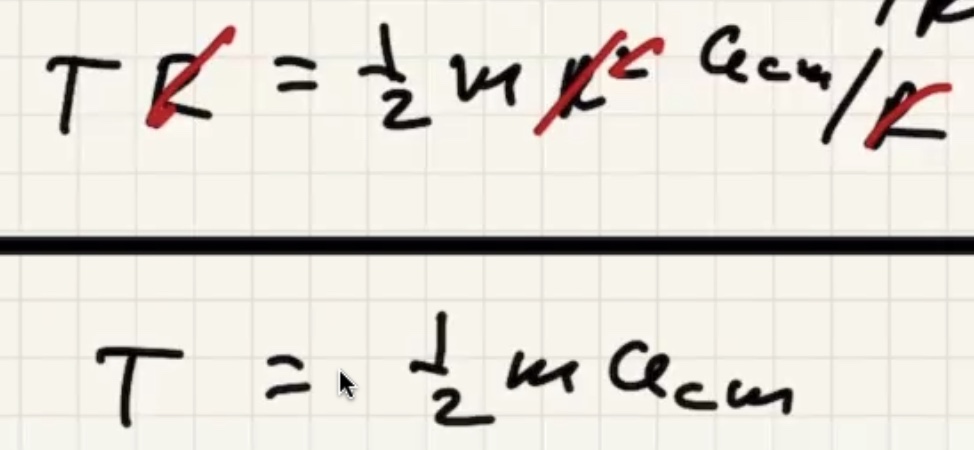
Can use these to solve the equation:

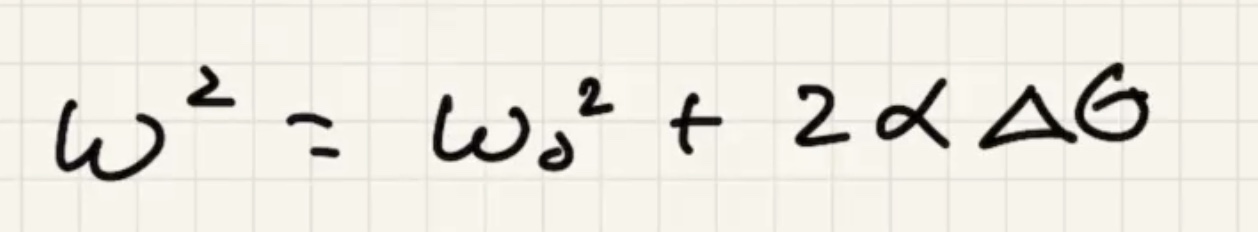
We’re looking for velocity of the center of mass $v_{cm}$:

Regarding the moment arm

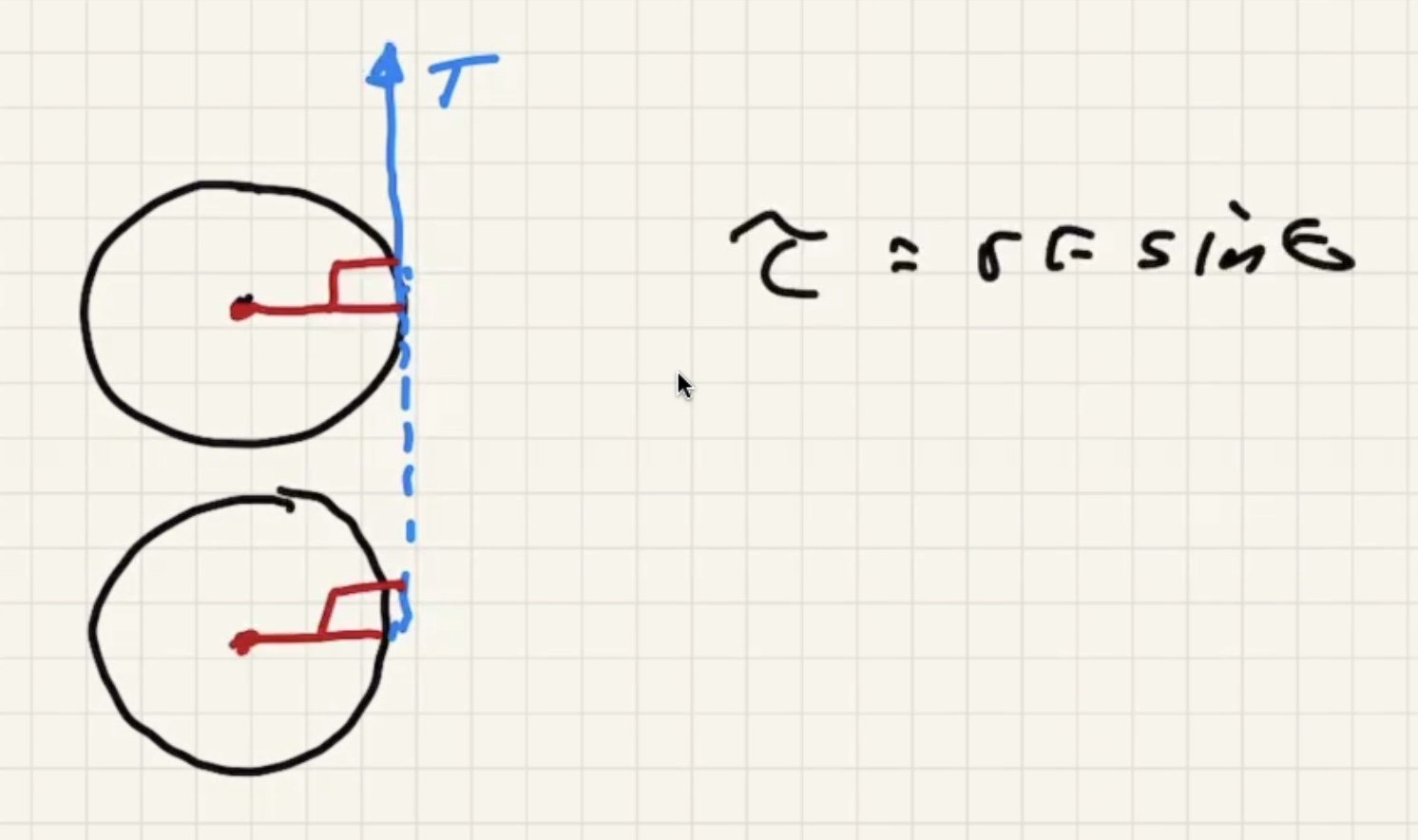
Since the string is always tangent to the circle it is always perpendicular to where it is attached. Therefore $\theta = 90$