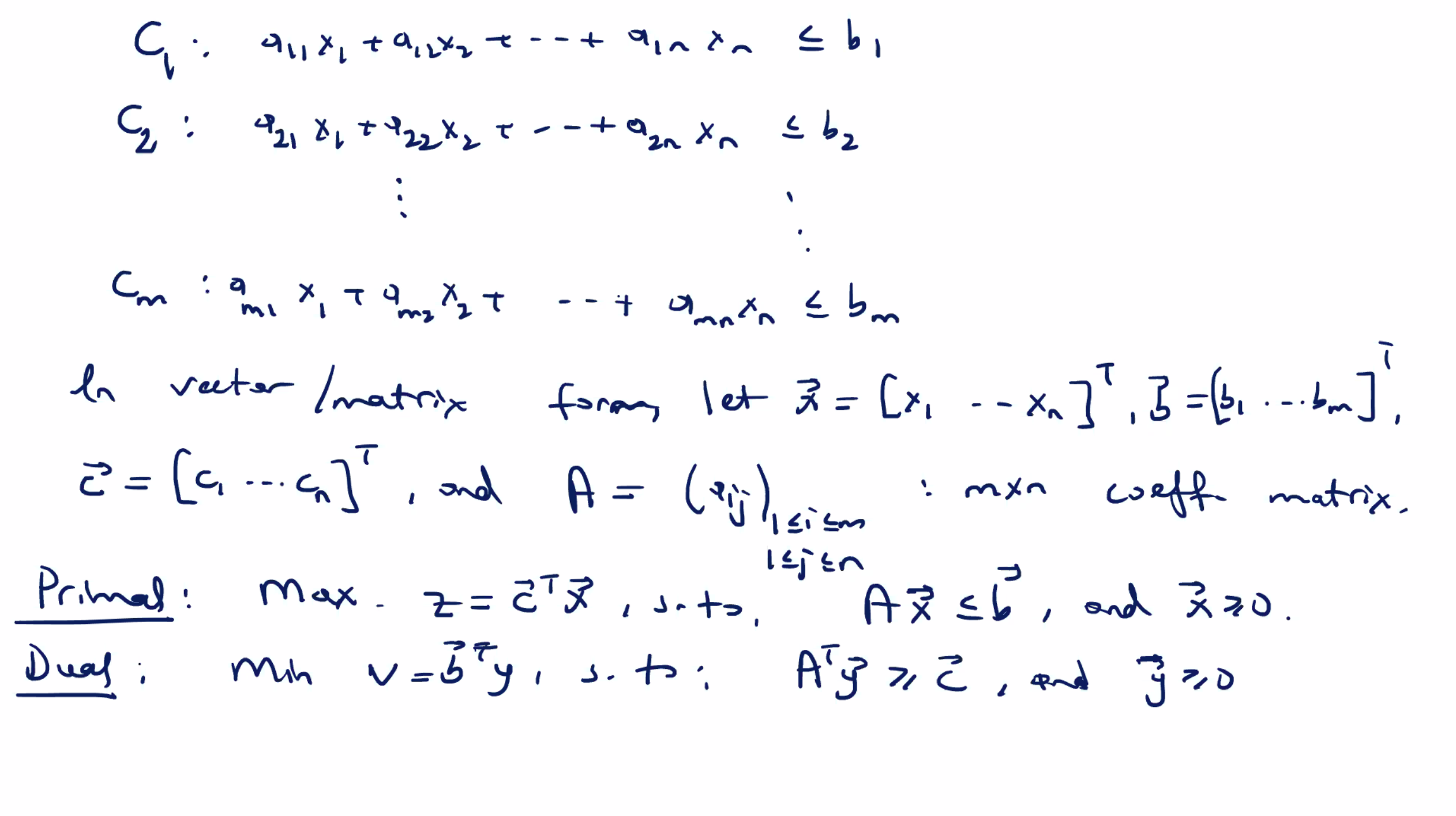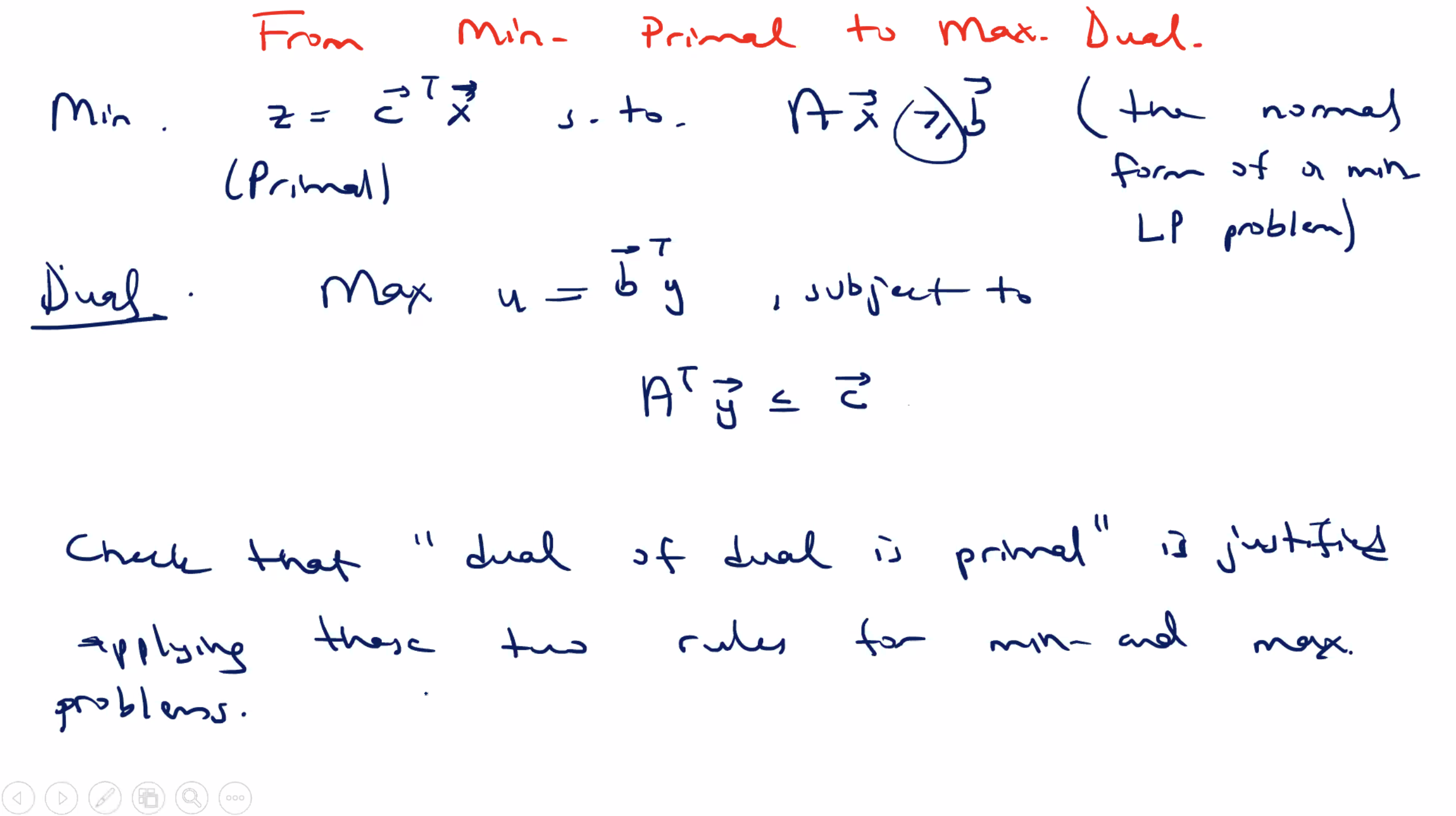Duality #

So lets find the dual of a previous problem:

This is the primal problem, so lets look at the corresponding dual problem:

A dual problem is: another LP problem that is related to the primal problem with different constraints and objective function.

• This will be a minimization problem (for a maximization primal problem)
• Two constraints of the primal yield two decision variables fo rthe dual, say \( y_1 \) and \( y_2 \)
• To determine the coefficients of the objective function, ie minimize \[ v= ? y_1 + ? y_2 \] . For the new constraints, lets first describe the primal problem in vector/matrix format, ie minimize \[ z = \bar{c}^T \bar{x} \] subject to \( A \bar{x} \leq \bar{b} \)

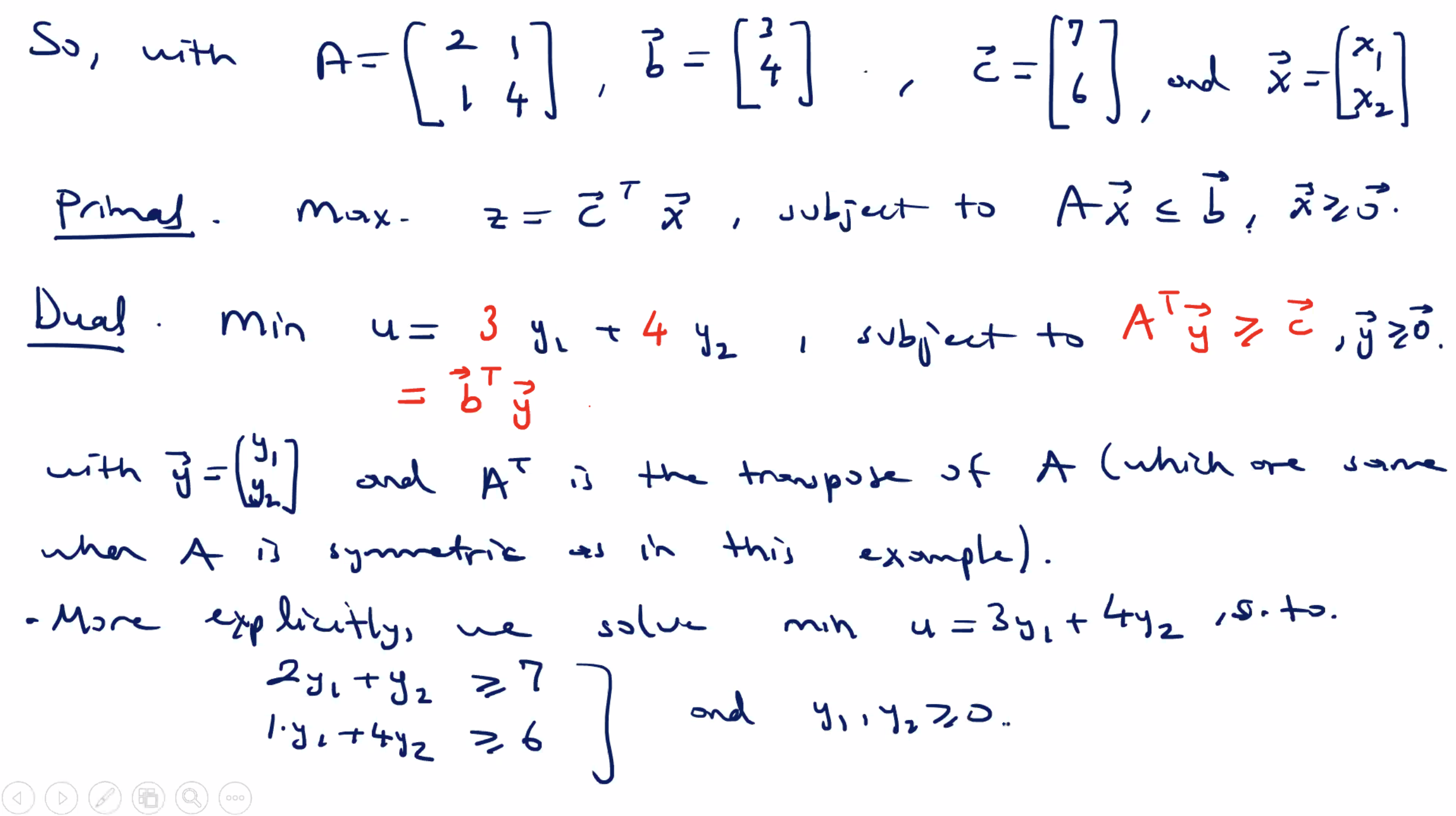
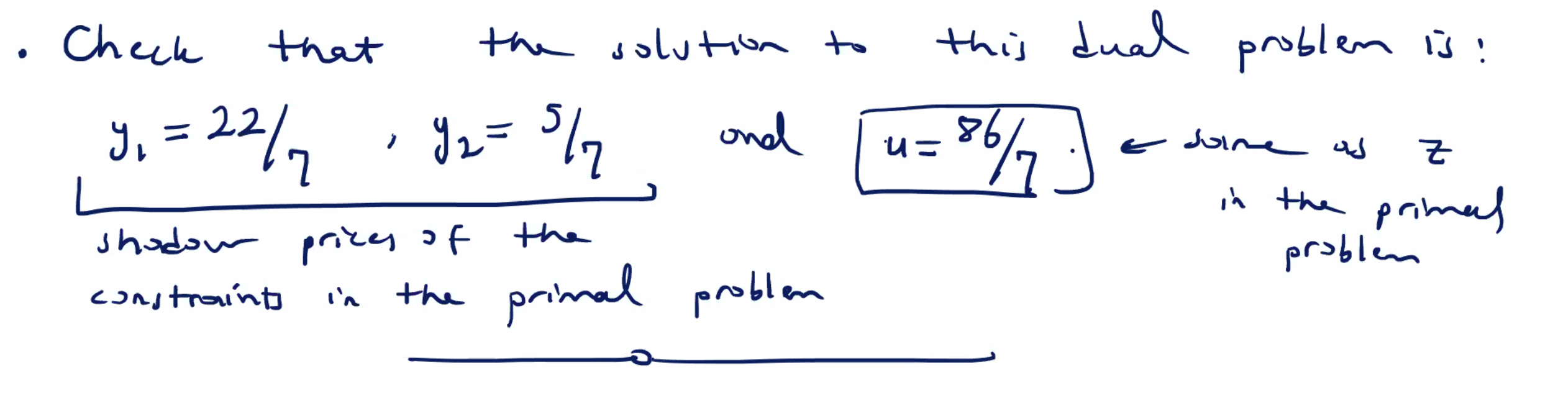
Another example from HW#2:

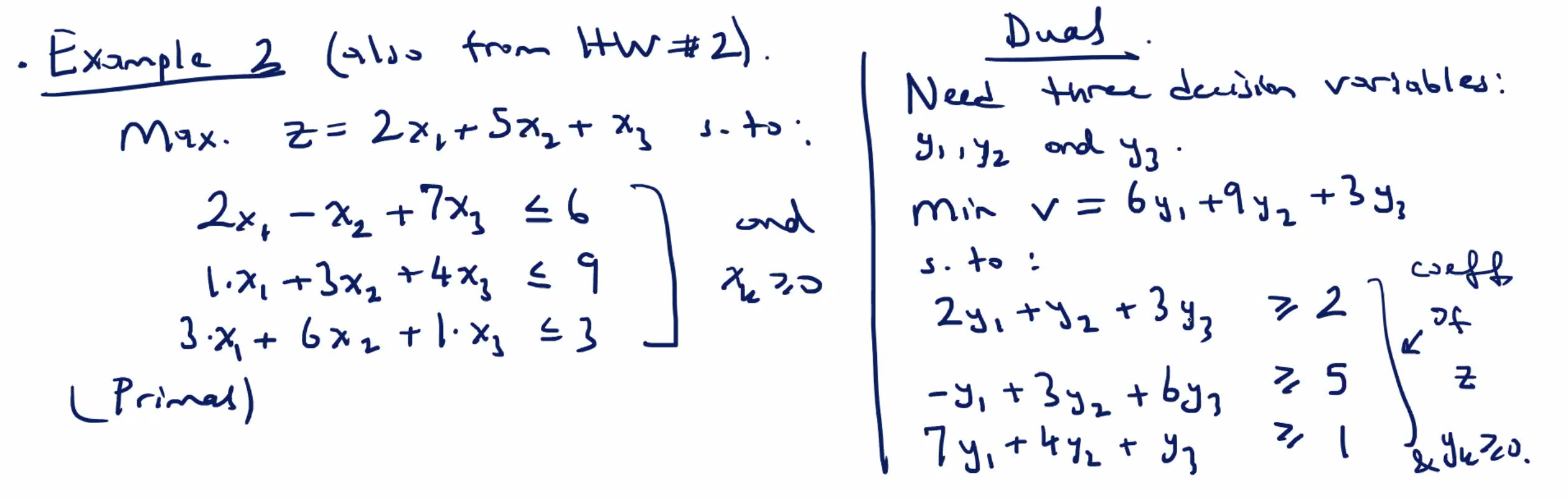
Duality problems with MATLAB #

For the primal function use linprog function setup of the primal problem with the following changes:

• use the negative transpose -A'
• swap b and C parameters in the function

[y, u]=linprog(b, -A', C, [], [], lb, [])

Another example #

• we can also switch from a primal LP minimization problem to dual LP maximization problem by reversing the steps used in the previous examples
• then, we get the fact that “dual of the dual is the primal”

A general format to switch from a primal to a dual:

Consider a generalp LP max problem of maximizing \( z=c_1 x_1 + c_2 x_2 + \cdots + c_n x_n \) with \( n \) decision variables and \( m \) linear constraints \( C_1, C_2, \ldots, C_m \) each with a “ \( \leq \) ” format.