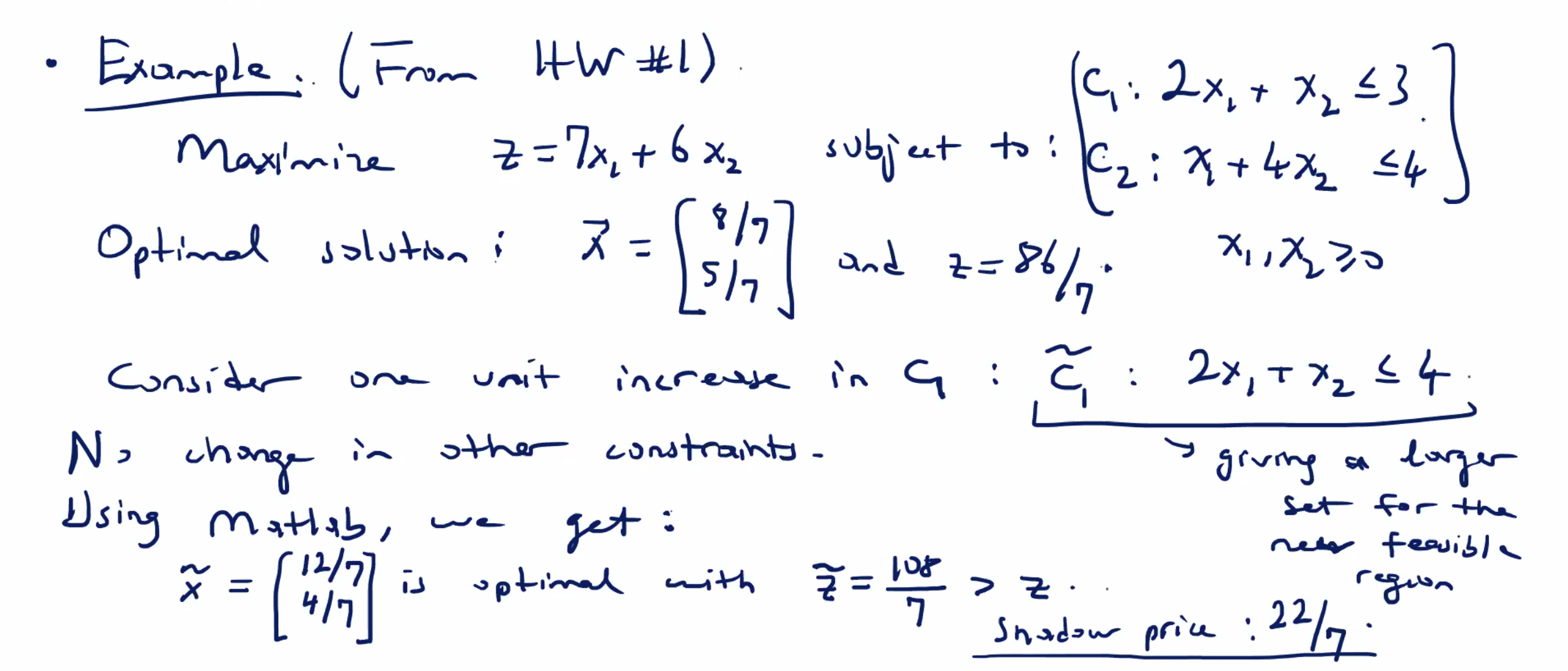Two phase procedure cont. #

Last problem finished #

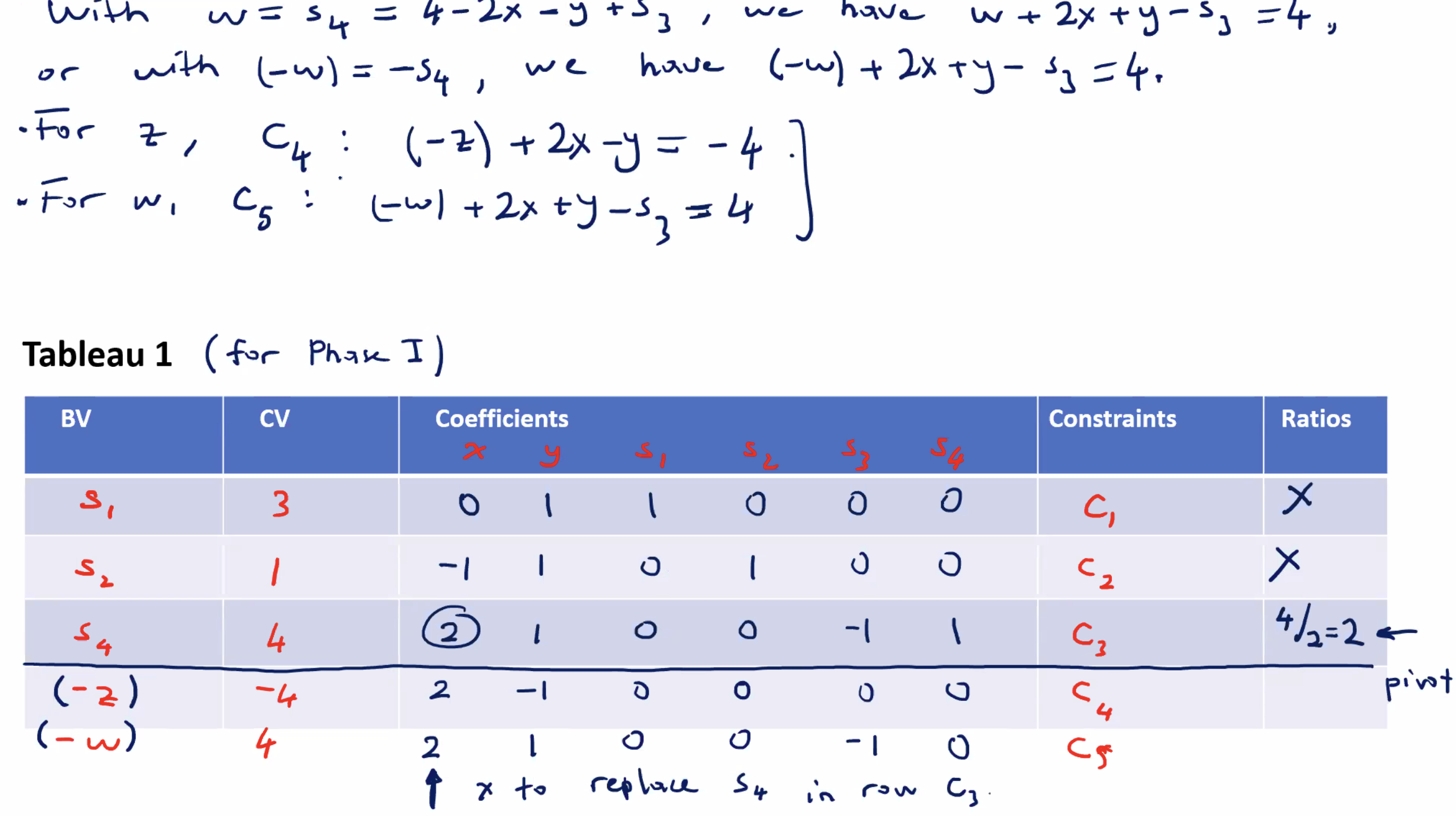
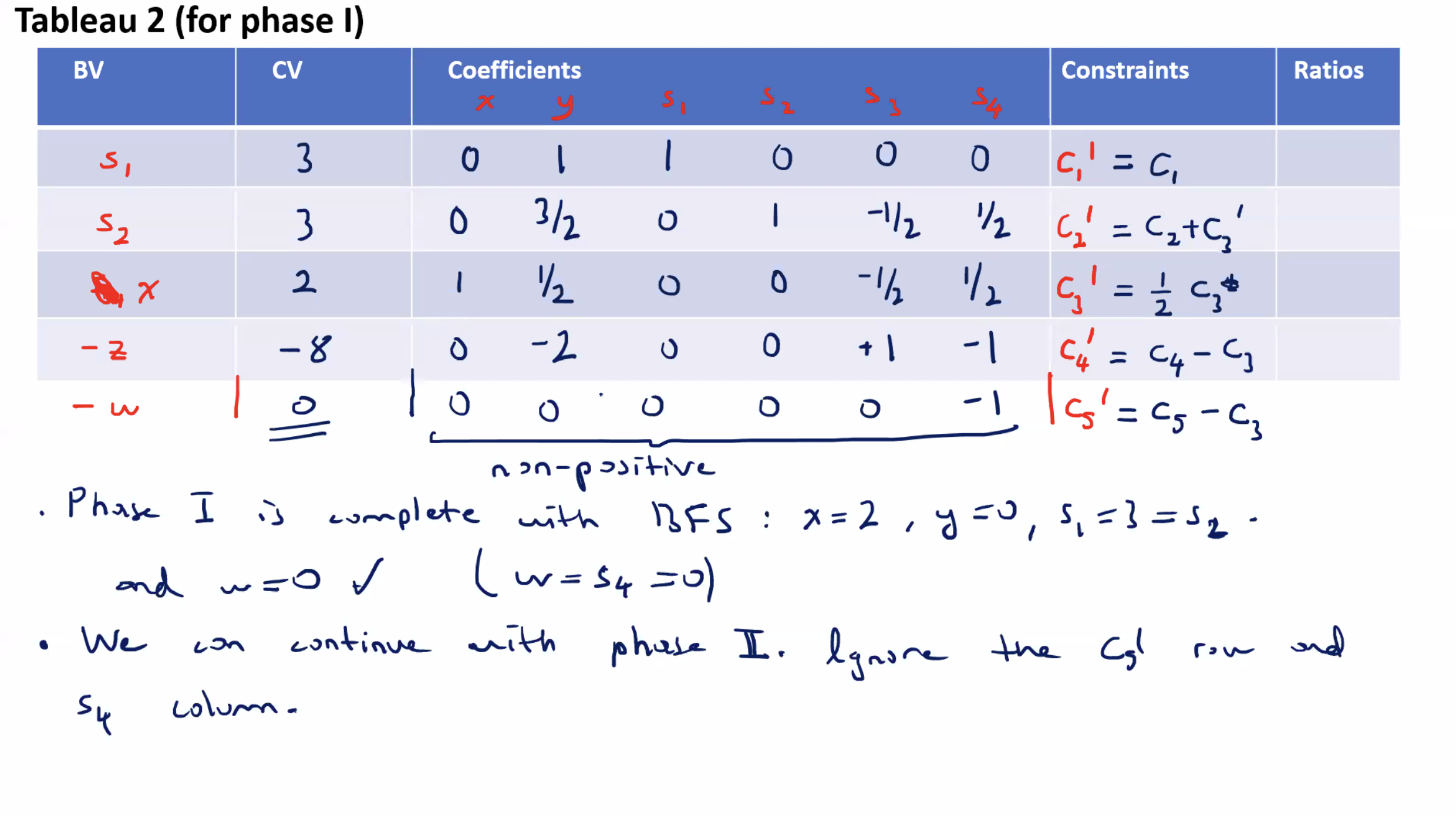
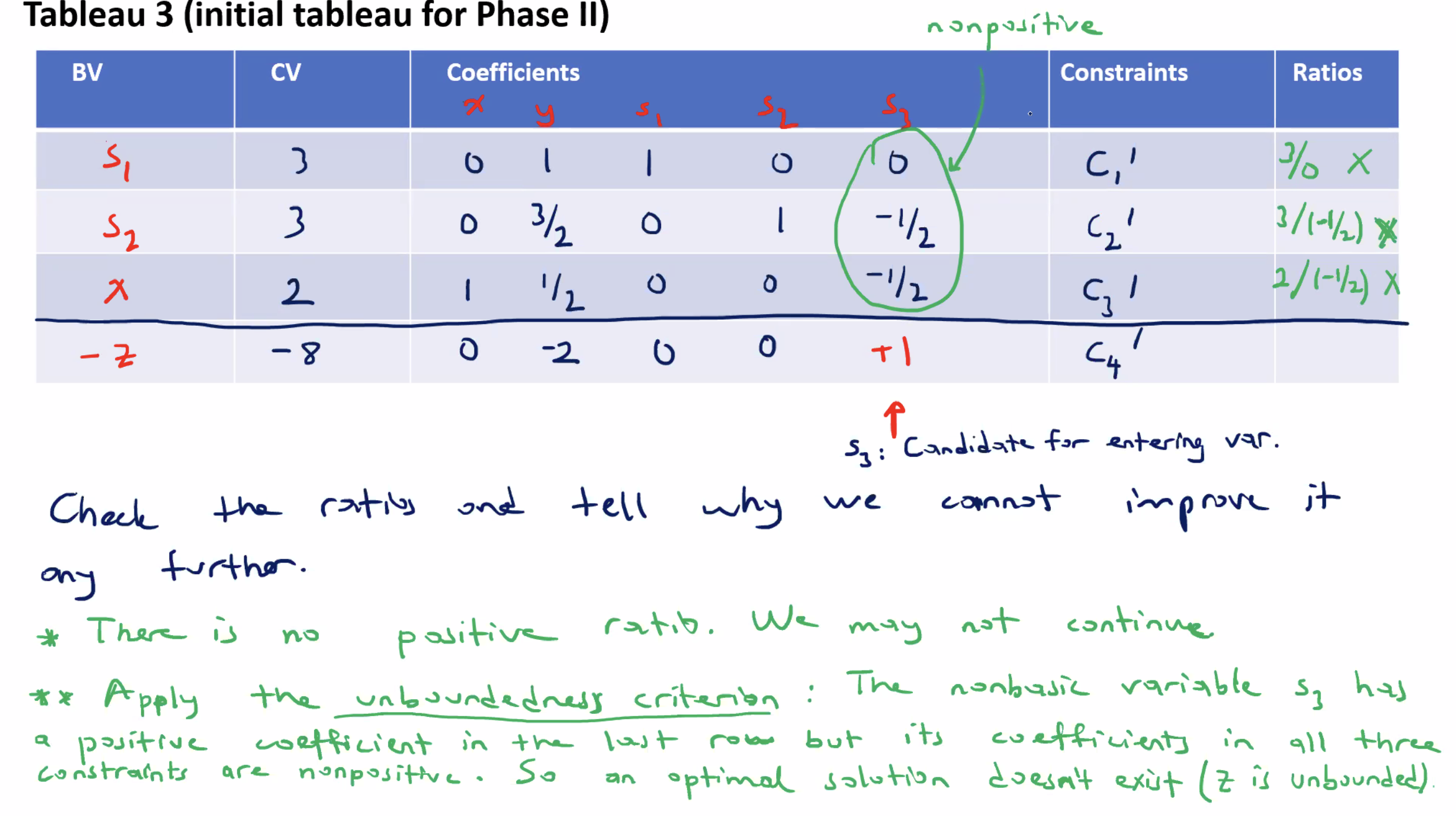
Detecting a non feasible region #

Can we recognize a non-feasible region using the two phase method?

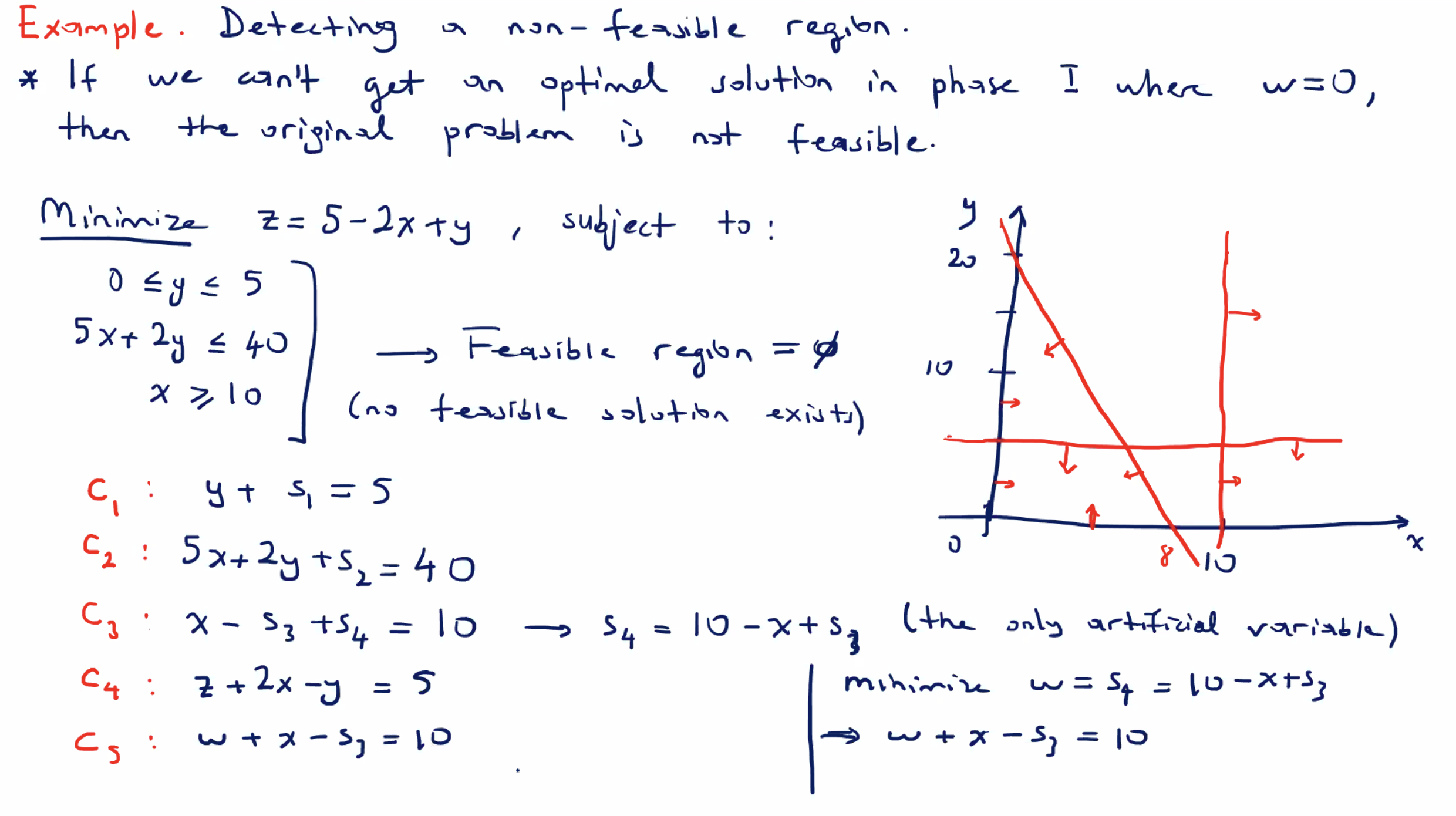
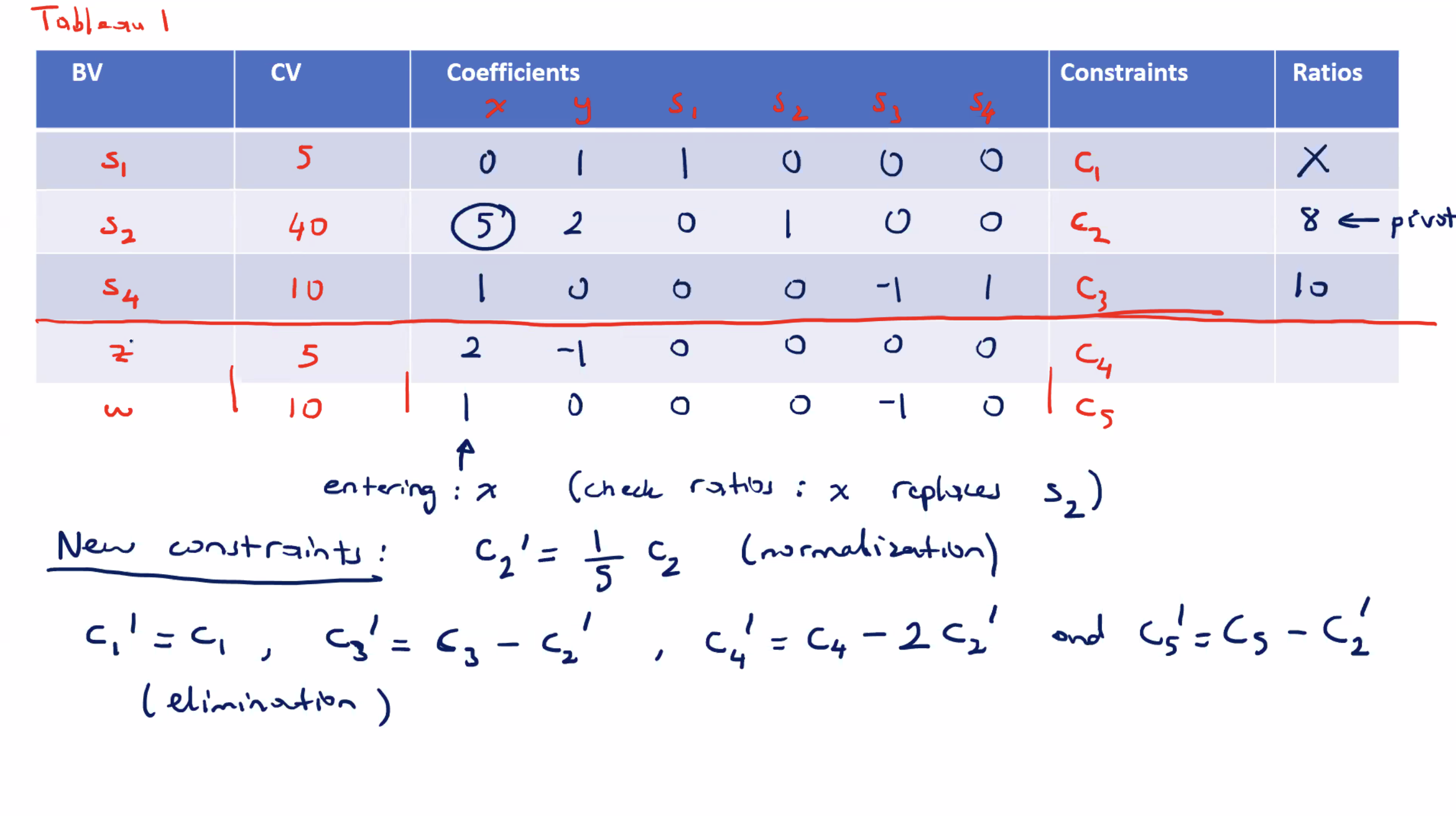
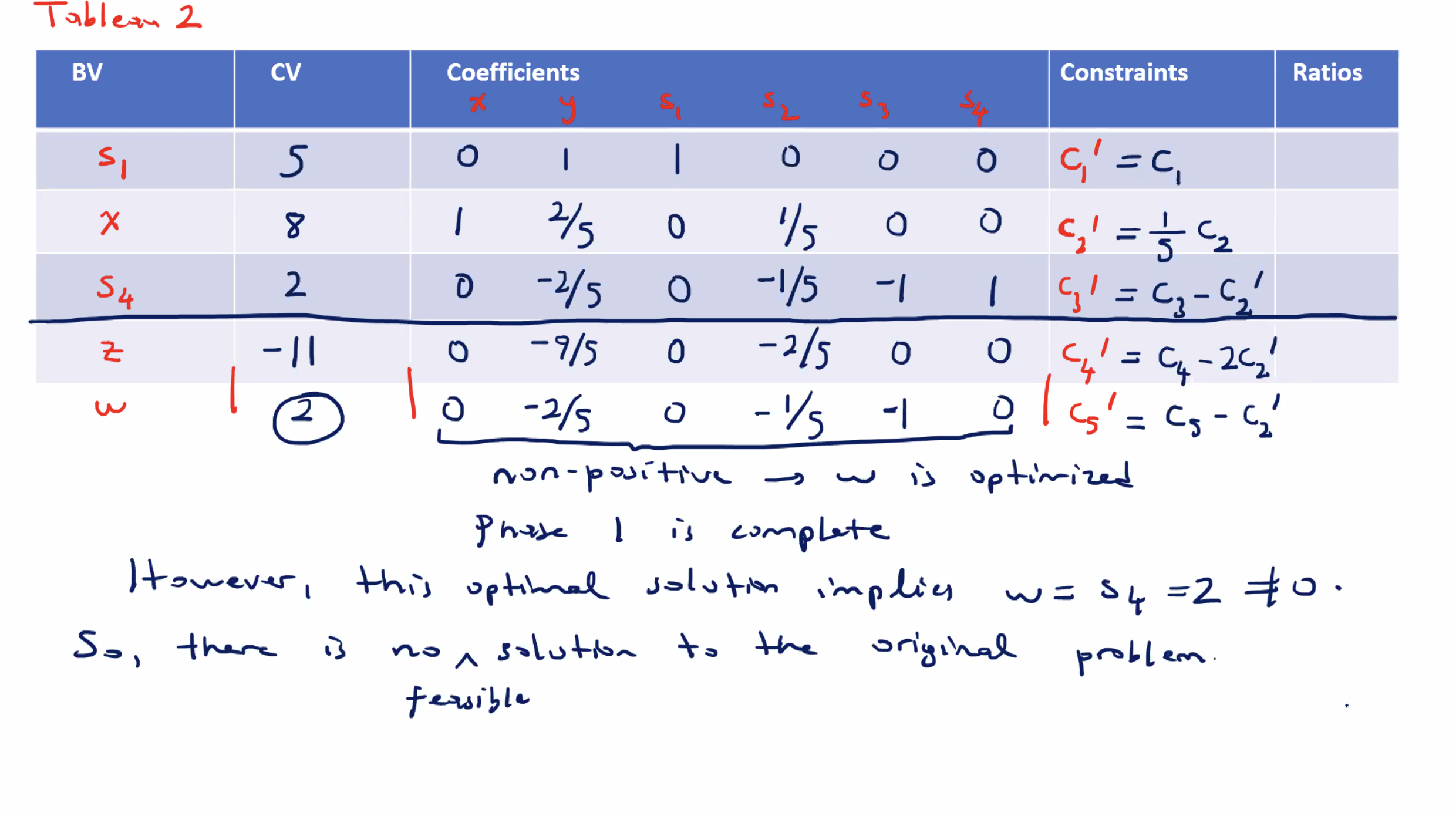
Phase one completes because we have all negative coefficients in the last row, but since \( w \not = 0 \) , there is no solution. We could solve this using Big M method where \( s_4 > 0 \) , and \( z' = z + M s_4 \) .

Applying the Big M method to an unbounded problem #

Using the problem from earlier:

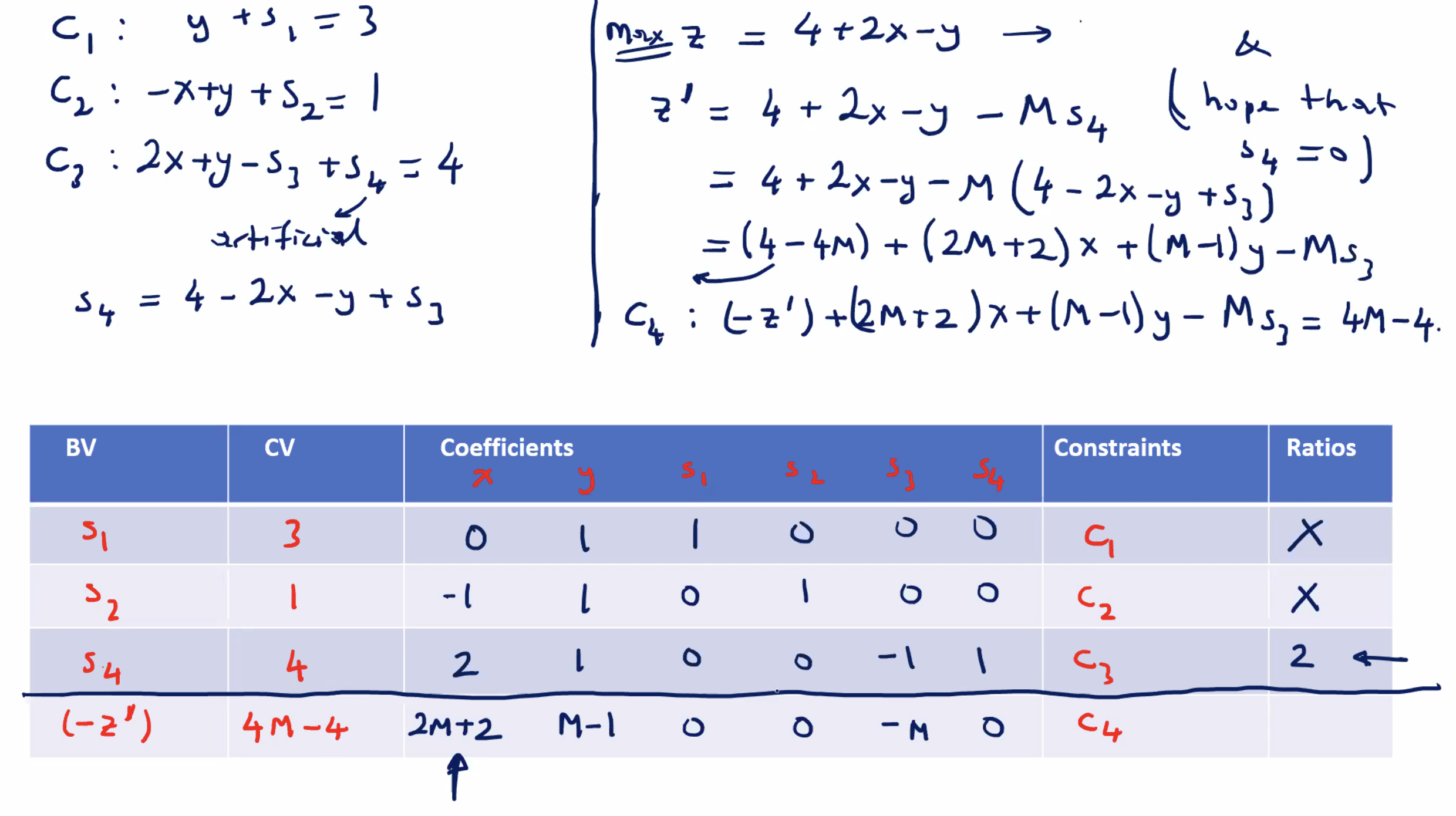
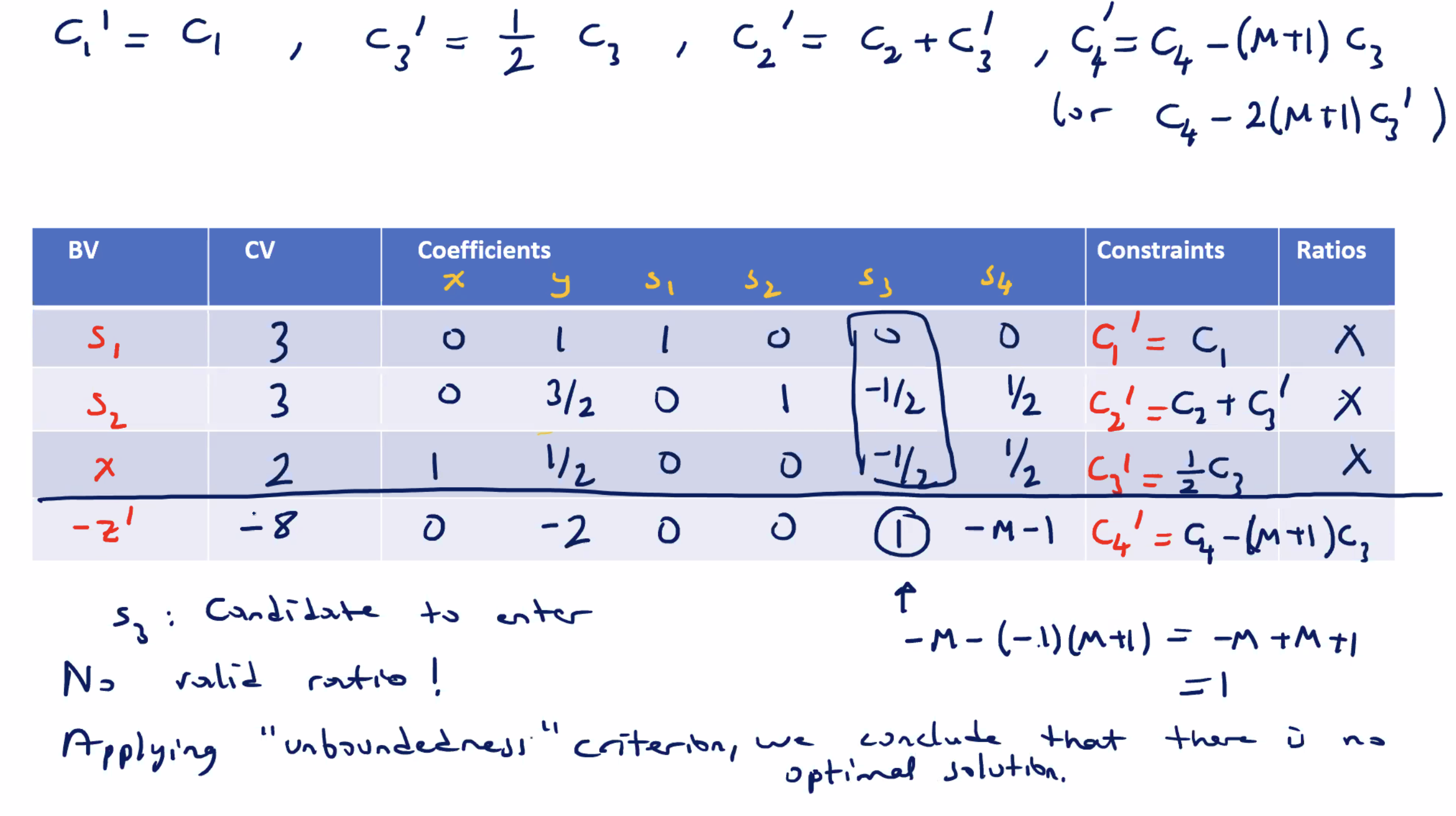
\( s_3 \) would be our next entering variable, however since there are no valid ratios (all negative), we cannot continue. So, applying the “unboundedness” criterion, we conclude that there is no optimal solution. This matches our result when we did it earlier using the two phase procedure.

Sensitivity analysis #

What happens if we are able to move the constraints around a little? What will the potential changes do the optimal solution?

We will cover

• The effect of changes in the constraints as well as in the lower/upper bounds on the optimal solution (vector) and on the optimal solution.
• Applications include
  • cost minimization, revenue maximization, profit maximization (the difference of the two)
  • marginal cost, revenue, or profit. The impact of an increase in one unit of a decision variable, for example.
• In LP problems, we also use the term shadow price for impact of a unit increase in a right hand side constant of a constraint on the optimal solution.

An example of finding shadow price #

We can use technology or some insight from the last simplex tableau for an optimal solution to determine the shadow price of a constraint.

Lets start with something where we already know the optimal solution, an example from the first homework: