Groups #

Diffie-Hellman is secure against any passive adversary using groups where the discrete log problem is hard.

A group is a simplification of a field, as it only has 1 operation (instead of 2).

In summary, a group

• is a set of objects (usually numbers) $G$
• has one operation (binary) that is closed, $G \times G \to G$
  • this is usually addition or multiplication
• has an identity
  • usually 0 in an additive group
  • usually 1 in a multiplicative group
• have invereses, $\forall x \in G, \exists y \in G$ such that $x \text{ op } y = \text{identity}$
• is associative, and commutative

Some examples of infinite groups

• the integers and the addition operator: $(\mathbb{Z} , +)$
  • 0 is identity
  • subtraction is the inverse
• the integers and multiplication is not a group, because 0 has no inverse: $(\mathbb{Z} , \times)$
• the rational numbers and multiplication is not a group, because 0 has no inverse: $(\mathbb{Q}, \times)$
  • however its almost a group if it weren’t for 0, so if we remove 0 it is a group: $(\mathbb{Q} -\{0\}, \times)$

A finite multiplicative group: $(Z^*_n, \times \mod n)$ , where $Z^*_n$ is the set of all $x \in Z_n$ and $\text{gcd} (x,n)=1$ .

To find a group in $Z^*_n$

1. Write all elements of $Z_n$
2. For each prime factor $x$ of $n$ , cross out all multiples of $x$ (including 0).
3. What ever is left is in $Z^*_n$

Finding a finite multiplicative group #

Lets find $Z^*_{12}$ .

We know that $$\begin{aligned} 12 = 2^2 \cdot 3 \end{aligned}$$

So we can cross out all the multiples of 2 and 3 in our list of numbers:

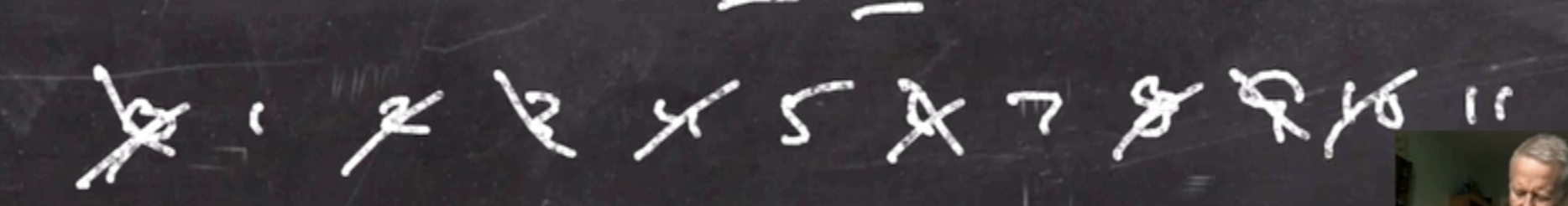
So $$\begin{aligned} Z^*_{12} = \{1,5,7,11\} \end{aligned}$$

which forms a multiplicative group $\mod 12$ .

So if we select a pair of these elements and multiple them and take $\mod 12$ , we get another items from the group. Each element happens to be its own inverse as well (this doesn’t always happen, but each element will have an inverse).

We are interested two finite groups that have a hard discrete log problem:

• $Z^*_p$ where $p$ is prime $$\begin{aligned} Z^*_p = \{1, 2, \ldots, p-1\} \end{aligned}$$ This is always guaranteed to be a group (0 is thrown out), and it is also a large group (no holes). The operations is $\times \mod p$ .
• The additive elliptic curve group.

Elliptic curve groups #

• https://wiki.crypto.rub.de/Buch/en/download/Understanding_Cryptography_Chptr_9---ECC.pdf

• This group is related to geometry (suggested by the name elliptic curve). Defined by the equation $$\begin{aligned} y^2 = x^3 + ax + b \mod p \end{aligned}$$
  • The set of objects in the group is all the integer points on the curve.
  • Not all of the points on the line are in the group, only those that have an integer for their $(x,y)$ coordinates.
  • The identity is $0$
  • The inverse of $(x,y)$ is $(x,-y)$
  • The operation is defined as addition $$\begin{aligned} \text{identity} = \text{point} + \text{inverse of point} \end{aligned}$$
  • To add a pair of points, define a secant line that goes through both points (which will be guaranteed to intersect the graph in exactly one other place) This new point is the reflection point, where the result is the inverse of that reflection
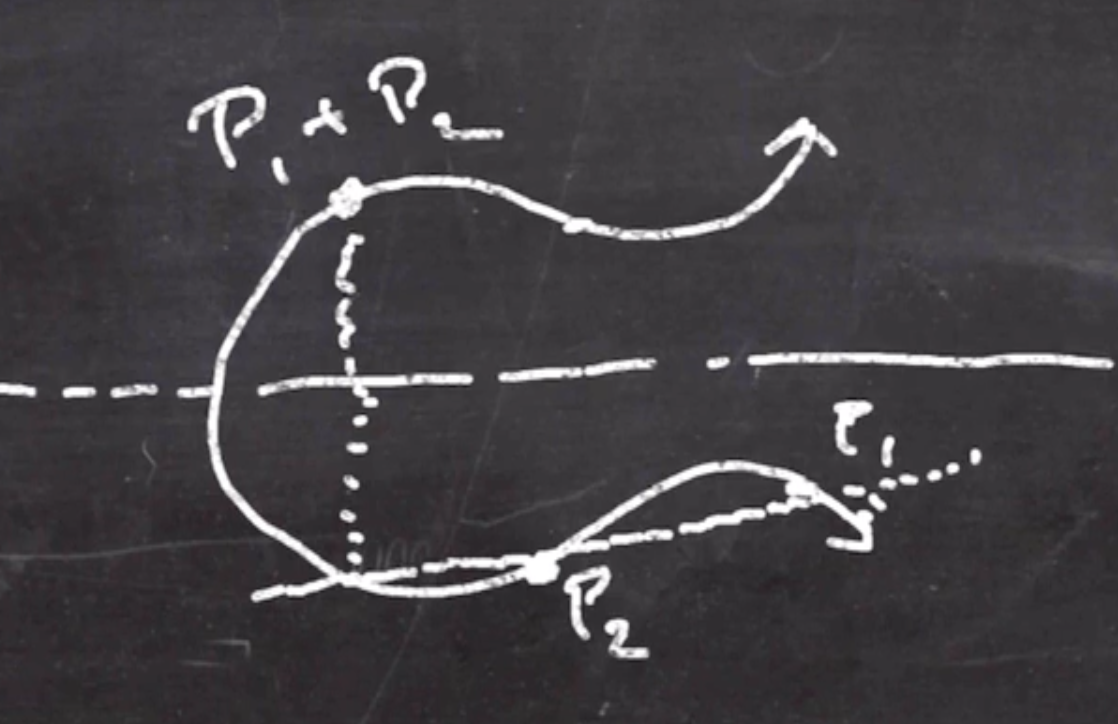
  • If we add a point to itself, define a tangent line that goes through the point, and take the inverse of the reflection point

Elliptic curve groups are good for efficient cryptography because the numbers only have to be 200-500 bits long.

Facts about groups #

If $G$ is a group, and $x \in G$ , then $x^{|G|} = 1$

Recall that $x^i$ in a multiplicative group is defined as

and in an additive group it is defined as

So consider $G = Z^*_7 = \{1, 2, \ldots, 6\}$

• We can raise an item from the group to the size of the group to demonstrate $$\begin{aligned} 3^6 \mod 7 = 1 \end{aligned}$$
• If we list out the powers up to the size of the group power, we get some interesting patterns $$\begin{aligned} 1^0 &= 1 \\ 2^0 &= 1, 2^1 = 2, 2^2 = 4, 2^3 = 1 \\ 3^0 &= 1, 3^1 = 3, 3^2 = 2, 3^3 = 6, 3^4 = 4, 3^5 = 5, 3^6 = 1 \end{aligned}$$ An element that goes through the entire group before returning to 1 is called a primitive (sometimes called a generator).

If $G$ and $H$ are groups that use the same operation, and $H \subseteq G$ , then $H$ is a subgroup of $G$ .

Each of the sets generated in the above example is a sub group (where $3$ generates the entire group).

So consider $H = \{1,2,4\}$ , the set generated by $2$ in $G$ above,

• The same operation is defined in the subgroup: $\times \mod 7$
• $1$ is the identity ( $1$ will always be in the subgroup)
• Inverses exist, ie $$\begin{aligned} 2 \times 4 \mod 7 = 4 \\ 4 \times 2 \mod 7 = 2 \end{aligned}$$
• Therefore, $H$ is a subgroup of $G$

The size of the subgroup that $x$ generates is called $x$ ’s order.

So, the order of a primitive element is the full size of the group. Also, every order divides the size of the group.

So since $|Z^*_7| = 6$ , and the order of 2 is 3, so $3 | 6$ .

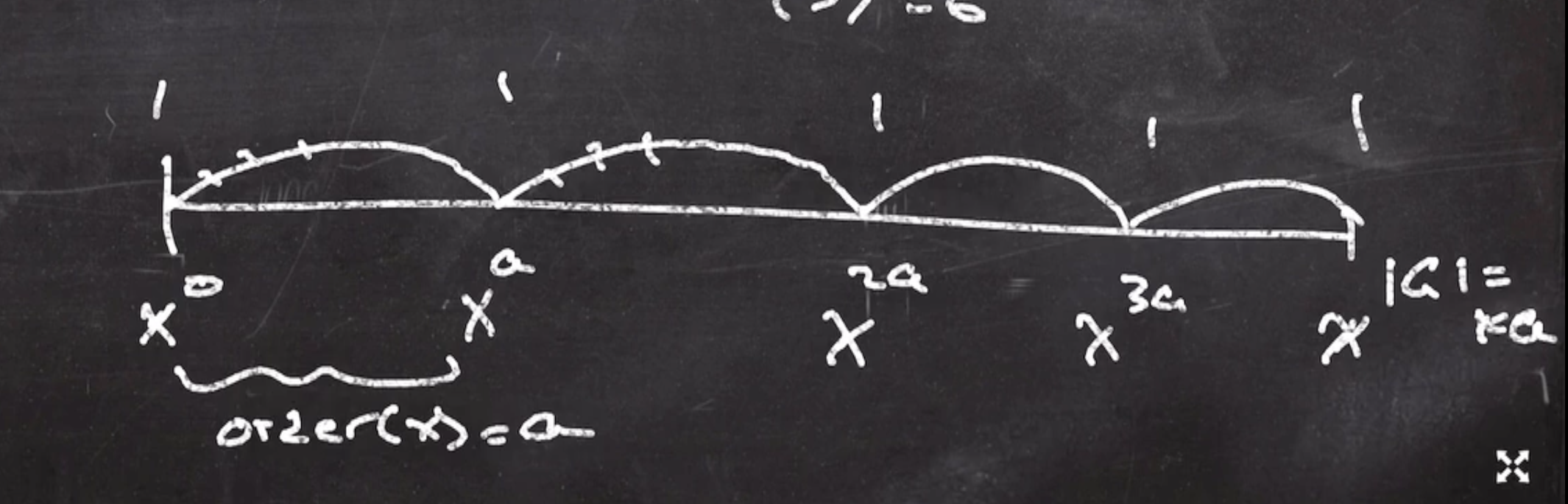
Diffie-Hellman using elliptic curve groups #

If we’re doing a Diffie-Hellman key exchange, we can use groups and generators

• group $G$
• generator $g$

Recall that the key exchange is as follows

• Alice chooses $x$ where $0 \leq x < \text{order} (G)$
• Alice sends $g^x$ to Bob
  • $g^x$ means to apply the group operator $x$ times, it may be additive or multiplcative
• Bob chooses $y$ where $0 \leq y < \text{order} (g)$
• Bob sends $g^y$ to Alice
• The shared secret is $g^{xy}$

Since the base $g$ is known, the secret is basically “how many times was the group operator applied?”

Using elliptic curves (since it is an additive group), the key exchange is as follows

• There is a known point $P = (a,b)$
• Alice chooses $x$ where $0 \leq x < \text{order} (P)$ , and sends $xP$
• Bob chooses $y$ where $0 \leq y < \text{order} (P)$ , and sends $yP$
• The secret is $xyP$

So how do we multiply an integer and a point? Recall that we can do exponentiation based on the bit pattern of the exponent with a combination of adding and squaring. 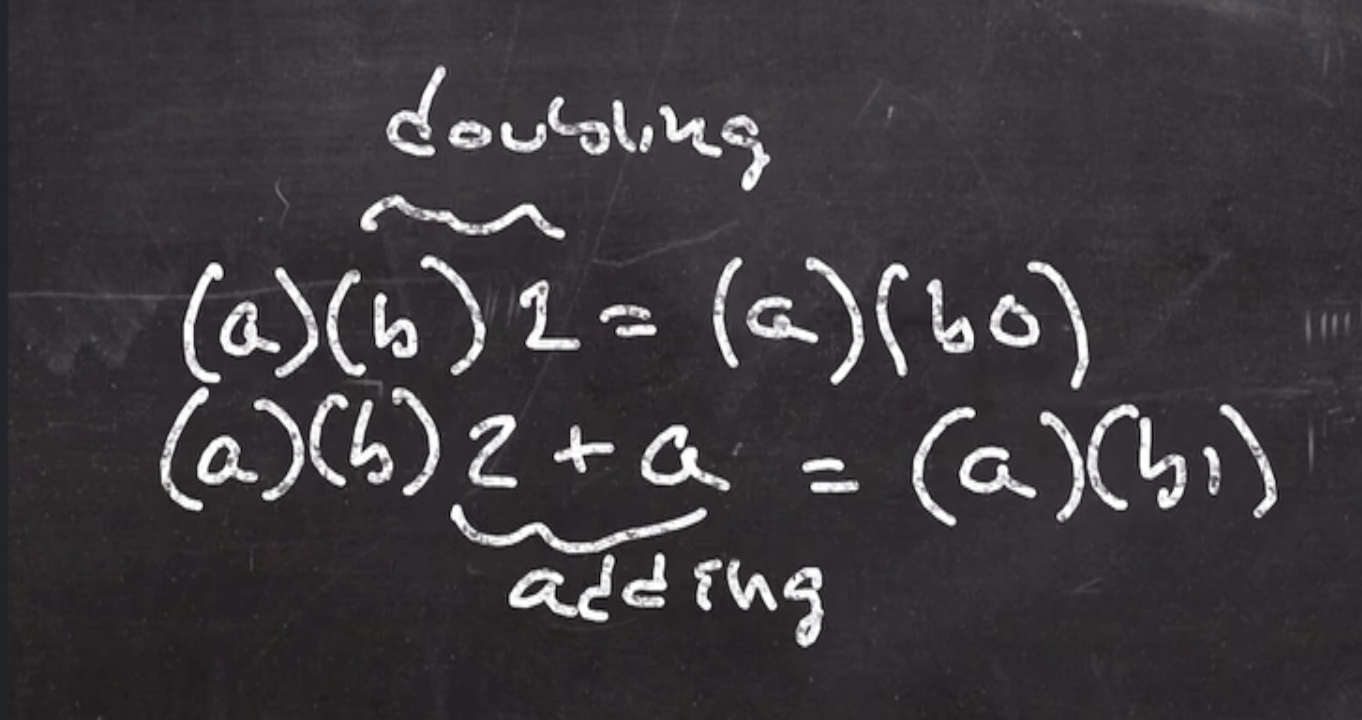Multiplication can be done via a combination of doubling and adding (both defined in an elliptic curve group), based on the bit pattern of the values.

mult(a,b):
    let b[1] ... b[n] = b in binary
    acc = 0
    for i from 1 to n:
        acc = acc + acc
        if b[i] = 1
            acc = acc + a
    return acc

Cryptographic systems #

Random number generation #

Random number generation might be the number one use of cryptography. Random number generation is used a lot in

• Games
• Simulation
  • Simulations run with a lot of random inputs and get a lot of outputs.
• Randomized algorithms
  • For something like quicksort, the worst case can be $O(n^2)$ when the array is already sorted. We can pick pivot points randomly to solve the worst case.

All of these uses need a high quality random number generator. If there is any bias, then the outputs will be bias. So we want our random number generators to be indistinguishable from truly random.

The cryptographic security model provides this indistinguishability we need.

Fortuna (2003) #

Fortuna is a pseudo-random number generator (PRNG). Used in FreeBSD and Apple operating systems.

Fortuna is made up of 2 parts

The random generator’s algorithm has

• a state $(k,c)$ where
  • $k$ is a 32 byte key
  • $c$ is a 16 byte counter
• a block cipher $E$ , we’ll use AES-256
• a cryptographic hash function $H$ , we’ll use SHA-256

GenRand(n):
    for i from 1 to ceiling(n/16):
        output E(k, c)
        c = c + 1
    k = E(k, c) || E(k, c + 1) // key update
    c = c + 2

• // key update line avoids birthday bound issues, and gives backward security, because this step is non-invertible
• The key is the start of the algorithm, so it must be random. So where the key come from?

The entropy collector

// s is a string with some entropy
Reseed(s):
    k = H(k || s)
    c = c + 1

• The entropy of $k || s$ is the sum of the entropy of $k$ and the entropy of $s$
• $k$ ’s entropy will be $\text{min} (\text{entropy} (k||s), 256)$
• Notice that the counter is incremented at the end of the entropy collection.
• The string $s$ comes from something like mouse clicks or keyboard taps
• $k$ is only as uncertain as $k || s$
  • If $k || s$ is as unpredictable as a random 256 bit string and $H$ behaves like a public random function, then $k$ is uniform.

Note: Entropy (unpredictable data) is additive.

So, a lot of entropy should be collected and $H$ should be a good hash function. The string $s$ is produced via unpredictable events like mouse clicks and keyboard taps.

Entropy #

A measure of uncertainty.

A process with $t$ bits of entropy is as uncertain as a random $t$ bit string.

For example

• A coin flip, can be heads or tails, has the same uncertainty of a 1 bit string: $0$ or $1$
  • 1 bit of entropy
• A sequence of 2 coin flips, HH HT TH TT, has an uncertainty of 2 bits
• A six sided die, can be 1 2 3 4 5 or 6, all equally likely. More uncertain than a 2 bit string, but less uncertain than a 3 bit string.
  • So, it has in between 2 and 3 bits of entropy
  • If $x$ is a random variable with $k$ equally likely outcomes, then $x$ has $\log_2 k$ bits of entropy.
  • So, $\log_2 6 \approx 2.6$ bits of entropy

If we have 3 different groups of people that all want different snacks, with this probability:

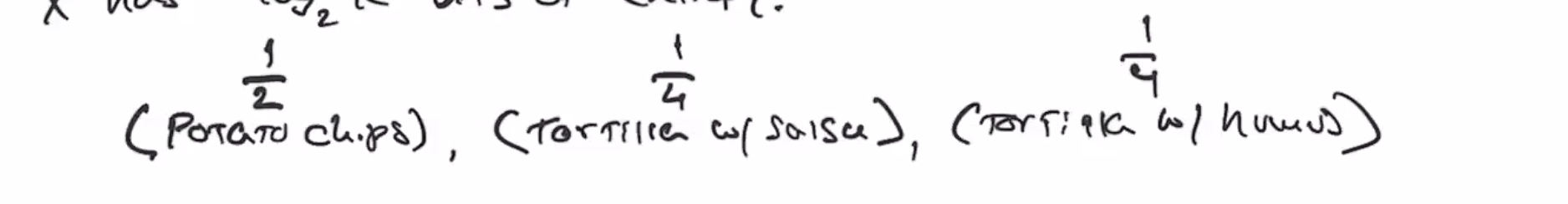
There is less entropy if there is an outcome that is more likely. The most entropy possible is when each outcome’s chance is all the same.

• If all outcomes had $\frac{1}{2}$ probability, then there is 2 possible outcomes, so 1 bit of entropy
• If all outcomes had $\frac{1}{4}$ probability, then there is 2 bits of entropy
• Then take a weighted average, $\frac{1}{2} + \frac{1}{4} \cdot 2 + \frac{1}{4} \cdot 2 = \frac{3}{2}$
• So out snack scenario has the same entropy has a 1.5 bit string

Entropy is defined as $$\begin{aligned} \text{entropy} = - \sum_{x \in X} P(X=x) \log_2 P(X=x) \end{aligned}$$

Entropy collection #

The second part of Fortuna requires that the key is seeded with a string with high entropy. The entropy collector is made up of

• A state, with pools $P_0, \ldots, P_{31}$ each empty (pools are strings).
• Sources, $s_1, \ldots, s_i$ , copy data from unpredictable sources, like mouse clicks and key presses, to pools in a round robin fashion.
• A reseed counter, starting at 0

These pools are being replenished via the sources as a background process, so when the random generator needs a key it is ready. The first thing that the random generator checks if a reseed is needed.

if P[0] has enough data and last reseed > 100ms ago
    s = ""
    reseed counter += 1
    for i from 0 to 31
        if 2^i divides reseed counter
            s = s || p[i]
            p[i] = ""
    Reseed(s)

• the check if 2^i divides reseed counter means that pool $p_0$ participates in every reseed, but pool $p_1$ participate every other reseed, pool $p_2$ will participate in reseeds 1,2 …

This helps thwart an adversary to flood a system with events with low entropy.

Forward security comes from entropy. Entropy keeps the adversary from knowing the future.