Alternatives to RSA #

RSA was invented in the 1970s and patented it. Alternatives came about because of the licensing fees that RSA used to require.

Recall that the RSA problem is

• Given \( x^e \mod n \) , \( e \) , and \( n \) , find \( x \) .
• This is hard, and thats why RSA is secure.

Recall the related problem, the discrete logarithm problem

• Given \( x^y \mod n \) , \( x \) , and \( n \) , find \( y \) .
• This is a similar problem, and it is also hard to find \( y \) .

In the 1980s cryptography started to be based on groups and discrete log. The discrete logarithm problem is defined over a group.

This is usually based on the multiplicative prime group \( Z^*_p \) , where

• the identity is the number 1
• the operation is multiplication \( \mod p \)

Note: The prime number has increased because of security over time, where now \(p\) may be 2000-4000 bits long. In response to the larger and larger modulus, there is a group called an elliptic curve group, where the values are around 200-500 bits long.

How to encrypt using a group – ElGamal encryption #

ElGamal, a researcher from Stamford in the 80s, published a paper that defined a signature scheme and an encryption scheme based on the discrete logarithm problem. Read more.

The encryption scheme can be thought of as a Diffie-Hellman key exchange over time.

• Alice lets \( g^x \) be their public key, where \( x \) is private
• Later, Bob wants to encrypt something and send it to Alice, so he sends her \( g^y \) and also the encrypted message multiplied by the key, \( km \)
• The key is \( g^{xy} \)

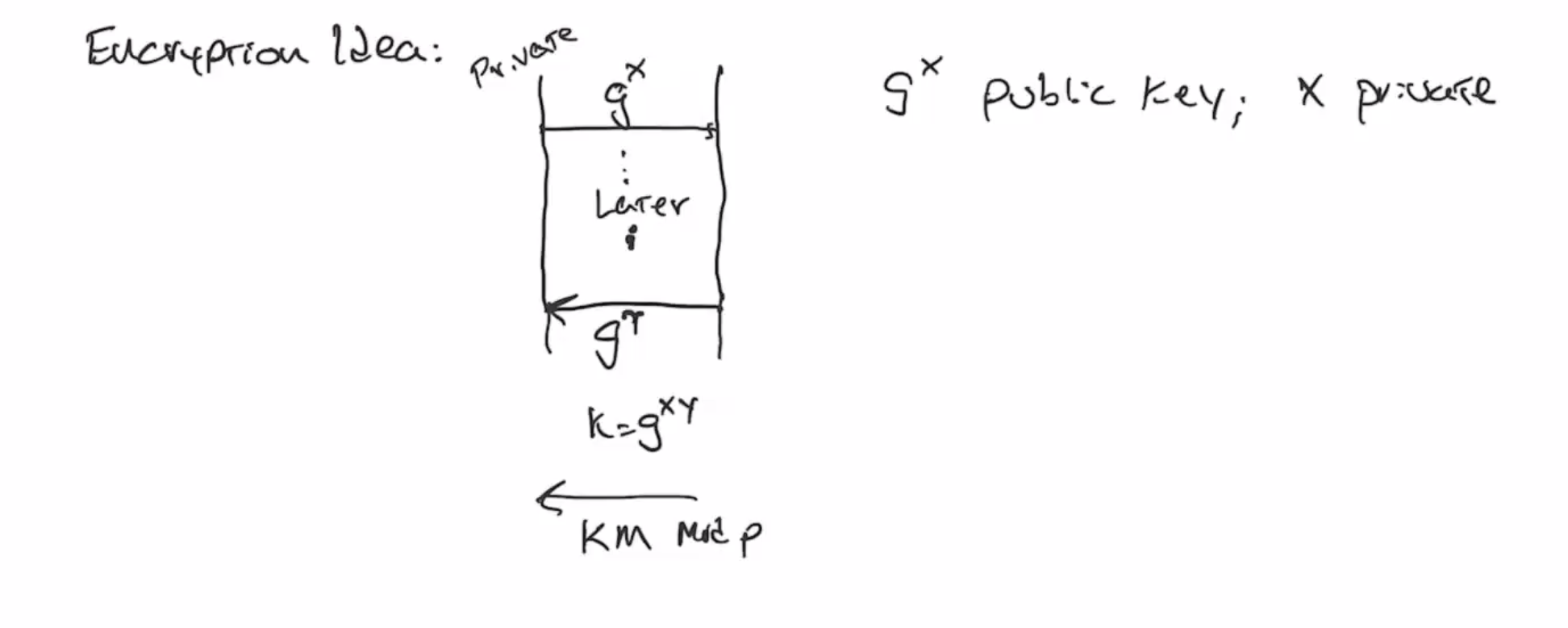
• To decrypt, \( m = k^{-1}(km) \mod p\)

In summary

• Key generation phase
  • define \( g,p \)
  • define secret exponent \( d \)
  • public key is \( (g, p, g^d) \)
  • private key is \( (g, p, d) \)
• To encrypt a value \( x \)
  • define \( e \) randomly where \( 0 < e < p \)
  • the encryption key is \( k = (g^d)^e = g^{de} \)
  • ciphertext is \( y = (g^e, kx) \)
• To decrypt a value \( y \)
  • we know \( d \)
  • calculate the inverse key \( k^{-1} = (g^{ed})^{-1} \)
  • calculate \( x = k^{-1} kx\)

Note: One of the setbacks of this scheme is that the ciphertext is made up of a pair, and is twice as long as \(p\).

ElGamal signatures #

A signature scheme called the ElGamal signature scheme. This is harder to visualize (its number theory magic with the best attack being discrete logarithm).

The algorithm itself

• Key generation
  • define generator \( g \)
  • define prime modulus \( p \)
  • define cryptographic hash function \( H \)
  • define secret \( x \) where \( 1 < x < p-1 \)
  • public key is \( (g, p, H, g^x) \)
• To sign a message \( m \)
  • define a key \( k \) where \( 1 < k < p-1 \) and \( \text{GCD} (k, p-1) = 1 \)
  • define \( r = g^k \mod p \)
  • define \( s = (H(m) - xr)k^{-1} \mod (p-1) \)
    • \( H(m) = sk + xr \mod (p-1)\)
  • the signature is defined as \( (r,s) \)
• To verify a message \( m \) with signature \( (r,s) \)
  • Check for equality on \( g^{H(m)} = = x^r \cdot r^s \)
    • This works because \( g^{H(m)} = g^{xr + sk} \)

The DSA (digital signature algorithm) is similar to this scheme.

Optimizing groups #

Our first priority is security, but our second concern is efficiency.

Two ways to attack a discrete logarithm problem

• Apply math, where we defend using a large modulus \( p \)
• Bruce force, given \( g^x = y \) you can attack over time \( g^i = y \forall i\) . So if our \( p \) is 2000 bits long, it is overkill. It is necessary for thwarting attacks based on mathematics, but overkill for brute force.

We can’t lower the amount of \( p \) , because we need to defend against mathematical attacks. But we can lower the size of the group we work in, this gives us an avenue to optimize. Group sizes are recommended to be \( 2^{256} \) .

So

• Let \( g \) generate a sub group of size \( q \) , where \[\begin{aligned} g^a = g^{a \mod q} \end{aligned}\] If \( p \) is around 2000 bits long, and \( q \) is around 200 bits long, then this results in a 10x speed up.

An example

• Let \( p = 101 \)
• The order of \( 5 \mod 101 = 25 \) (order is how long the cycle around the modulus is, which is a subgroup of \( Z^*_p \) ). \[\begin{aligned} 5^{25} \mod 101 = 1 \end{aligned}\]
• So lets find \( 5^{80} \mod 101 \) \[\begin{aligned} 5^{80} \mod 101 &= 5^{25} \cdot 5^{25} \cdot 5^{25} \cdot 5^5 \mod 101 \\ &= 1 \cdot 1 \cdot 1 \cdot 5^5 \mod 101 \end{aligned}\]

How to create a prime group with a subgroup #

Fact

• In a cyclic group, every element generates a cyclic subgroup and its size divides the size of the full group. \[\begin{aligned} Z^*_7 = \{1, 2, \ldots, 6\} \end{aligned}\] The size of \( Z^*_p \) is \( p-1 \) . So the size of \( Z^*_7 \) is \( 6 \) , and the divisors of \( 6 \) are \( 1,2,3,6 \) . So the possible sizes of the sub groups are \( 1,2,3,6 \) .
• 1 generates a group of size 1, \( \{1\} \)
• 2 generates a group of size 3, \( \{2,4,1\} \)
• 3 generates a group of size 6, \( \{3,2,6,4,5,1\} \)
• 4 generates a group of size 3, \( \{4,2,1\} \) , notice it is identical to the other subgroup of size 3
• …
• 6 generates a group of size 2, \( \{6,1\} \)

Note: The last value in the group gives the subgroup of size 2.

Fact

• Every divisor of a cyclic group’s size has a subgroup (just 1) of that size.

• This gives us the idea to pick a large prime \( p \) where the size of the multiplicative prime group \( |Z^*_p| \) has a 256-bit prime factor \( q \) . \[\begin{aligned} |Z^*_p| = p-1 \end{aligned}\] So we need to find \( p-1 = nq \) for some \( n \) .

  An algorithm to accomplish this

  q = 256 bit random prime
  do
      n = random (2000-256)-bit long even number
      p = nq + 1
  while p not prime
  

  • This results in \( q \) is prime, \( p \) is prime, and \( q | (p-1) \)

Fact

• If \( G \) is a cyclic group and \( a \in G \) , then \( a^{|G|} = 1 \)
• So, if \( x \in Z^*_p \) then \[\begin{aligned} 1 &= x^{p-1} \mod p \\ &= x^{nq} \mod p \\ &= (x^n)^q \mod p \end{aligned}\] If \( x^n \) is not \( 1 \) , then \( g \) generates a size \( q \) subgroup. So this gives us an algorithm to find \( p,q \) , and \( g \) :
  1. pick \( p \) and \( q \) , such that \( p = nq + 1 \) for some integer \( n \) .
  2. repeatedly pick \( x \in Z^*_p \) . If \( x^n \mod p \neq 1 \) , then \( g = x^n \mod p \) .

A subgroup example #

We will use

• \( n = 2 \)
• \( q = 41 \)
• \( p = 83 \)

So our group is \( Z^*_{83} = \{1, 2, \ldots, 82\} \)

We can look for \( x \) where \( x^n \mod p \neq 1 \) .

So the order of \( 4 \mod 83 \) is 41.

So we can use our optimization as \( 4^{x \mod 41} \mod p = 4^x \mod p \)