Problems with RSA #
RSA has some problems, namely
- RSA can be distinguished easily
- a black box is either a RSA encryption scheme or random bits
- it is easy to distinguish between these 2 worlds by sending a 0 bit (or a 1) to the box and see what comes back, and so in the RSA box \[ \begin{aligned} 0^e = 0 \end{aligned} \]
- if we restrict the numbers to large inputs then this becomes better
- RSA leaks information \[\begin{aligned} y_1 = \text{RSA}(x_1) \\ y_2 = \text{RSA}(x_2) \end{aligned}\] If \( y_1 = y_2 \) then \( x_1 = x_2 \) . The information that is leaked is whether the plaintexts are the same.
- RSA is “malleable”. This means that changes to the ciphertext have predictable results on the plaintext. \[\begin{aligned} y = x^e \mod n \end{aligned}\] If we multiply \( y \) by \( 2^e \) and decrypt (all \( \mod n\) ): \[\begin{aligned} (y \cdot 2^e)^d &= (x^e 2^e)^d \\ &= ((2x)^e)^d \\ &= 2x \end{aligned}\] This is ultimately fixed by authentication.
So, in summary the main problems are:
- There is no randomization in RSA. Encrypting the same plaintext twice should yield different ciphertexts.
- The ciphertext is the result of math applied directly on the plaintext.
OAEP #
So the solution to these problems is the OAEP (optimal asymmetric encryption padding) padding scheme.
The structure of this padding is a Feistel structure.
Start by padding the rightside of the plaintext with 0s, then random bits:

This goes into a Feistel structure like so:
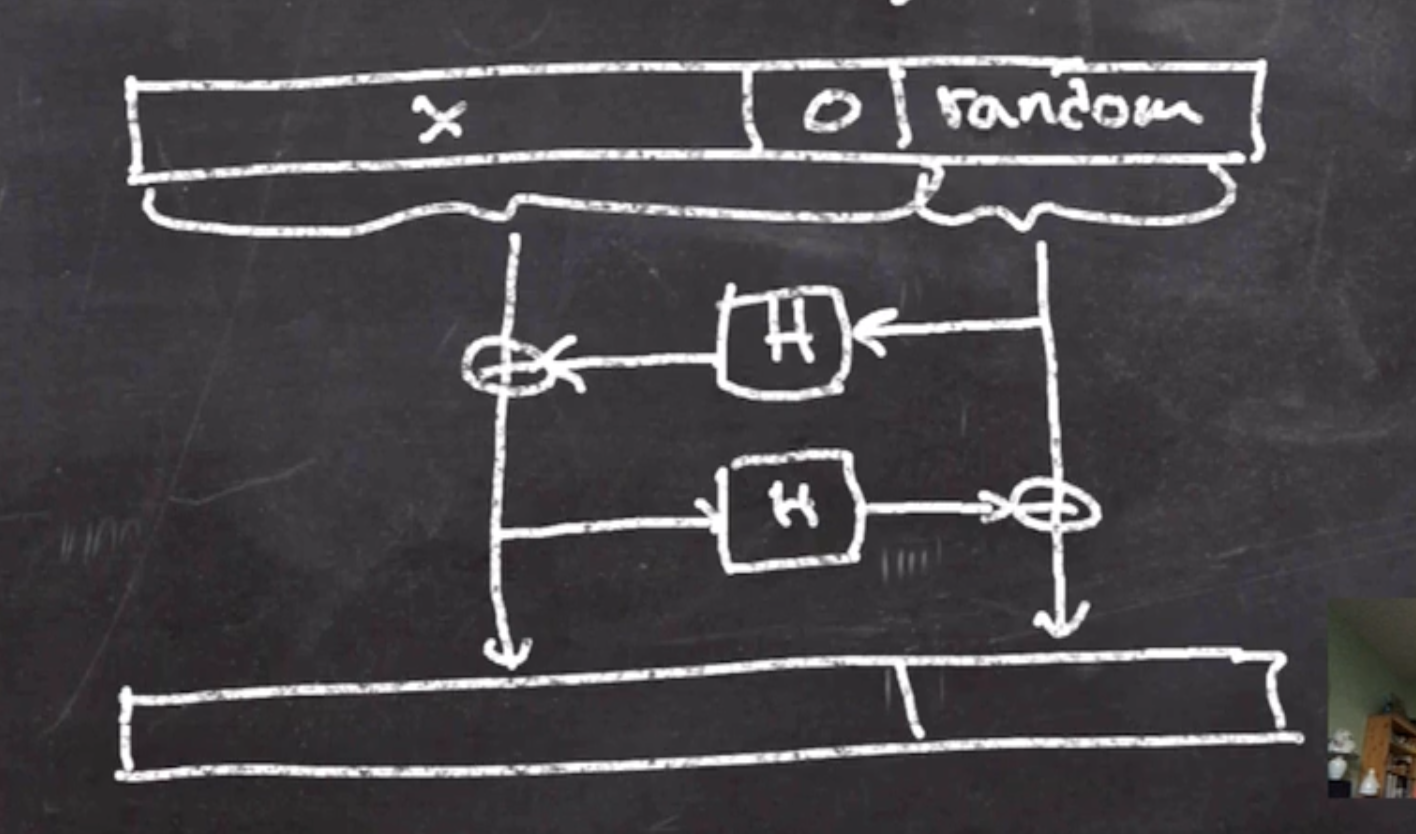
- Since this is a Feistel structure, it is invertible.
- The function \( H \) is a MGF (mask generation function). This is similar to the sponge construction with extended output (squeeze).
- The random portion is around 256 bits, likely something that has never been seen before (this fixes our main RSA problem).
- The 0 padding is around 64 bits
- \( x \) can be up to around 1700 bits
- The entire output should be indistinguishable from random
We can utilize this in our algorithm when encrypting using RSA
encrypt(x):
x' = OAEP(x)
return (x')^e mod n
When decrypting
- We decrypt using the textbook RSA, then
- de-pad using the inverse OAEP function
Authentication with RSA #
Authentication hashes when using asymmetric cryptography are called signatures.
When Alice sends Bob an encrypted message, she sends both the data and the signature.
To sign the data, Alice locks it with her private key,
\[\begin{aligned} \text{sign}(x) := x^d \mod n \end{aligned}\]Bob receives the data and the signature, and verifies that the message is in fact from Alice by unlocking it with Alice’s public key,
\[\begin{aligned} \text{verify}(\text{sig}) := \text{sig}^e \mod n == x \end{aligned}\]Since the goal in the RSA problem is
- given \( x^e \mod n, e, \) and \( n \) , it is hard to find \( x \)
- implies that \( x^d \mod n \) is hard to find hard without \( d \)
In order for the adversary to create a forgery, she would have to
- calculate \( x^d \mod n \) without \( d \) , which is really hard
- or find a collision in the hash function used when signing
The problem here is that our data has to be less that \( n \) , so we will solve this by instead taking a hash of the data and signing that.
Signing with a cryptographic hash #
Recall that a cryptographic hash is
- collision resistant
- preimage resistant
- 2nd preimage resistant
So we can use a hash function to hash our data, and then we will actually sign that.
\[\begin{aligned} \text{sign}(x) := H(x)^d \mod n \end{aligned}\]When we verify, we have to hash the data ourselves and check if its equal
\[\begin{aligned} \text{verify}(x, \text{sig}) := \text{sig}^e \mod n == H(x) \end{aligned}\]Diffie-Hellman key exchange #
Diffie-Hellman wiki entry
This solves the problem of actually getting the shared key to the other party. The Diffie-Hellman key exchange is setup in a way that even if the adversary is listening to the communication between Alice and Bob, they still have no way of calculating the actual shared key from the information divulged during eavesdropping.
This is based on the logarithm problem, for example when given \( 2 \) and \( 2^x \) , find \( x \) .
We can actually do this using a binary search technique. Since each time our search space is cut in half, it ends up being an algorithm to the order of \( O(\log x) \) .
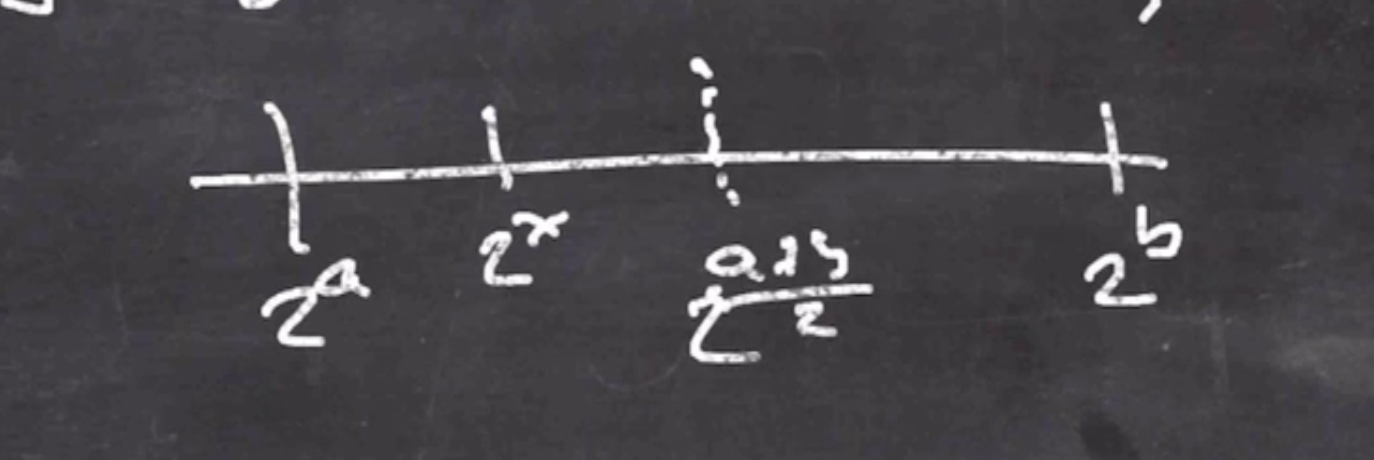
If we throw in a modulus on the logarithm, we cannot use this same binary search technique. This is called the discrete logarithm problem. This is what the Diffie-Hellman exchange is based on.
Discrete logarithm problem:
Given \( g,n \) and \( g^x \mod n \) , find \( x \) .
If \( g^x \) is large enough it will wrap around the modulus ring multiple times, and there will be no way to hone in on the target like in our binary search technique before. The modulus \( n \) is usually thousands of bits long.
How the exchange works #
Our goal is to establish a secret in plain sight.
What is known is
- a base \( g \)
- a modulus \( n \)
- Alice chooses a random value \( x \) in the range \( 0 < x < n \) .
- Alice sends \( g^x \mod n \) to Bob
- Bob chooses a random value \( y \) in the range \( 0 < y < n \) .
- Bob sends \( g^y \mod n \) to Alice
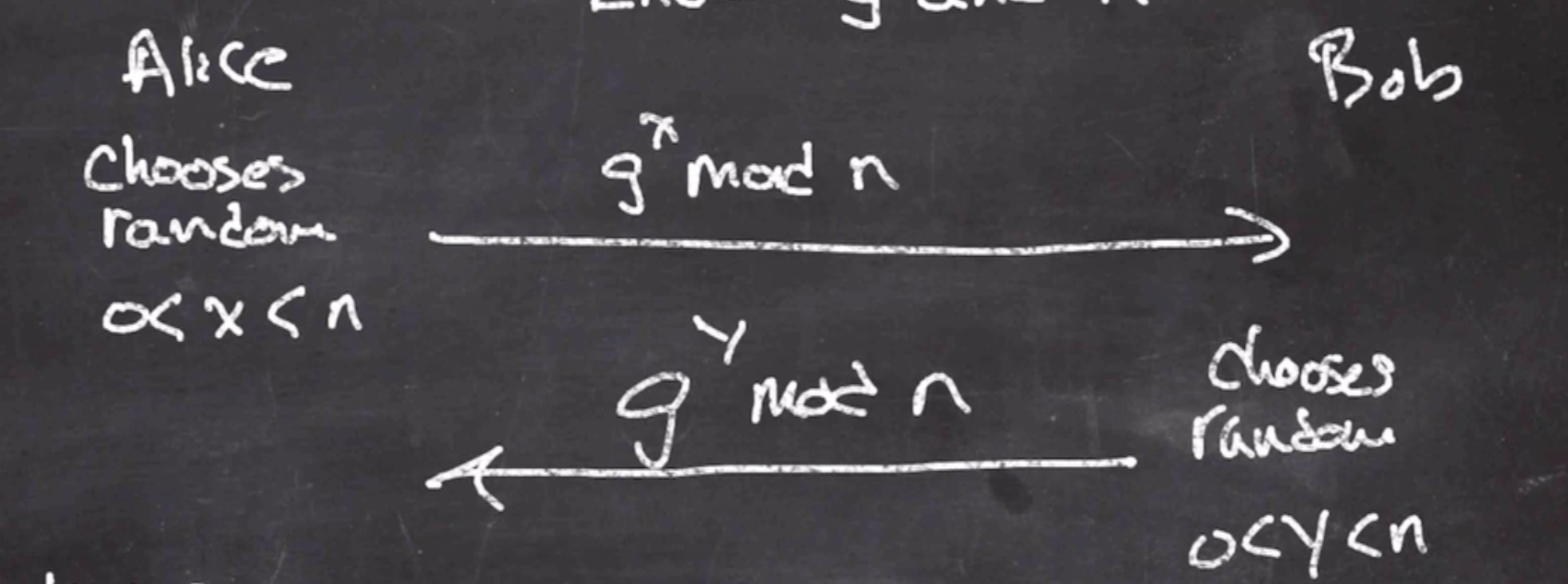
Alice knows
- \(x\), \(g^y\)
Eve knows
- \(g^x,g^y\)
Bob knows
- \(y,g^x\)
So the shared secret is \( g^{xy} \mod n \) . Eve cannot compute this.
This situation is safe against the passive adversary (just eavesdropping).
Man in the middle attack on the key exchange #
Eve can manipulate the messages in the middle between Alice and Bob’s communication.
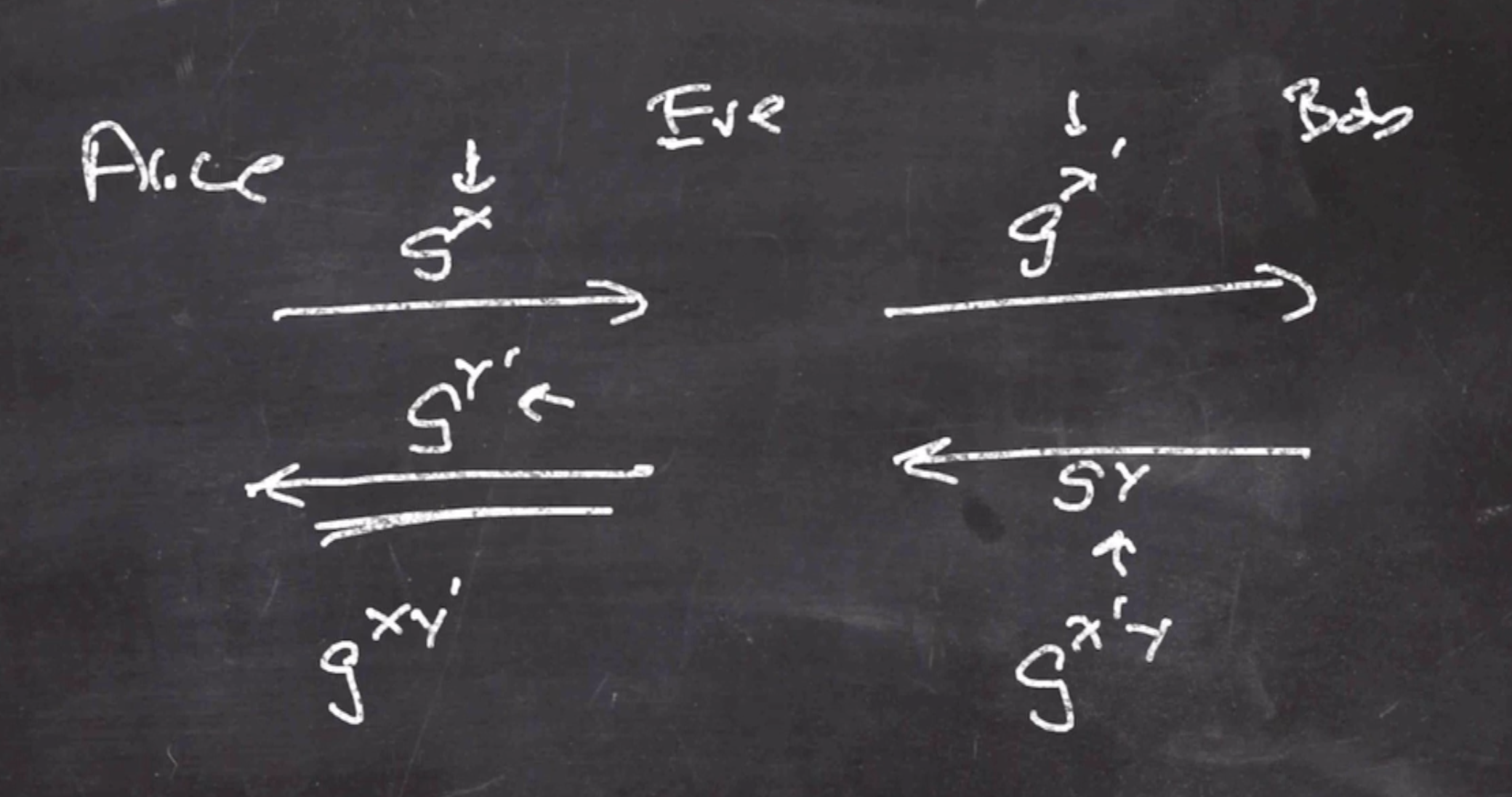
- Eve receieves \( g^x \) from Alice
- Eve sends \( g^{x'} \) to Bob, and receieves \( g^y \)
- Eve sends \( g^{y'} \) to Alice
Alice has now set up a key with Alice and a key with Bob. In this situation Eve is considered an active adversary.
We can solve this problem using authentication.