Intro to asymmetric encryption #

Until now, we’ve been using symmetric cryptography. This means that both Alice and Bob are sharing a secret key.

In asymmetric cryptography, Alice and Bob have their own secret keys. They also both have public keys.

Both public and private keys are created at the same time.

We want to provide these services using asymmetric cryptography:

Pros/cons #

In the real world, we first

1. use asymmetric cryptography to establish a shared key
2. use symmetric cryptography to encrypt the bulk of the data

This ends up getting the best of both worlds.

Discrete logarithm problem #

A logarithm using a modulus:

Given \( x,g, \) and prime number \( p \)

This is asking “ \( g \) to what power \( \mod p \) will give you \( x \) ?

All of the calculation is done \( \mod p \) , which makes the question a little harder than the normal logarithmic problem. Because for each time \( y \) is increased, the output is pretty much randomly distributed because it is wrapping around the ring when \( \mod p\) is calculated.

RSA problem #

Given \( x,e, \) and \( p \) , we need to find \( y \) :

Because of the \( \mod p \) , this makes finding \( y \) really difficult.

Exponentiation #

Since we are working on algorithms that work on huge numbers, we need to have a way to efficiently handle large exponentiation calculations.

For example if we’re calculating \( x^y \) , we may naively write an algorithm like

acc = 1
for i from 1 to y
    acc *= x

This is sufficient for most applications, but it starts to break down on very large numbers. The loop occurs to an exponential number of times relative to the number of bits in \( y \) .

If \( y \) is 32 bits long, it may take a few minutes to calculate the result. If \( y \) is 64 bits long, it will takes years to calculate the result.

We are working with \( y \) values around 2000-8000 bits long, the universe hasn’t been around long enough to calculate that result.

Instead, we should write our algorithm to be based on the length of the value, not based on the value itself.

Observe,

If we use the binary representation of \( y \) , to multiply by 2 we simple to a left shift 1 (concatenate a 0 on the end).

Notice that if we want to multiply by 2 and add 1 we can simply concatenate a 1 onto the end of \( y \) (so left shift then flip rightmost bit). This gives us a way to programatically create an exponent.

At any point, if we want to append a 0 we just square the number, if we want to append a 1 square then multiply by the base. For example, if we are calculating \( 3^6 \) :

This can be expressed as an algorithm,

// calculate x^y
pow(x, y)
    let y = y1, y2, ..., yn where yi in {0,1}
    acc = 1
    for i from 1 to n
        // always square
        acc = acc * acc
        // if rightmost bit is on (odd)
        if yi == 1
            acc = acc * x
    return acc

This is a \( O(n) \) operation, where \( n \) is the bit length of our exponent. This is good because we are looping relative to how many bits the number is represented in.

An example #

Lets calculate \( (4)^{11} \) :

1. first get the exponent in binary: \( 11 = \text{0b} 1011 \)
2. start at the multiplicative identity: \( 1 \) \[\begin{aligned} 4^0 = 4^{\text{0b}0} = 1 \end{aligned}\]
3. when we insert the first \( 1 \) , we square then multiply by base \[\begin{aligned} 4^{\text{0b}01} = 1^2 \cdot 4 \end{aligned}\]
4. we are now inserting a \( 0 \) , so we just square the accumulator \[\begin{aligned} 4^{\text{0b}010} &= (1^2 \cdot 4)^2 \end{aligned}\]
5. insert a 1, so square and multiply by base \[\begin{aligned} 4^{\text{0b}0101} &= ((1^2 \cdot 4)^2)^2 \cdot 4 \end{aligned}\]
6. insert last 1, square and multiply \[\begin{aligned} 4^{\text{0b}01011} &= (((1^2 \cdot 4)^2)^2 \cdot 4)^2 \cdot 4 \end{aligned}\]

GCD – greatest common divisor #

An algorithm developed by Euclid in 300 BC.

When given a pair of integers, it returns the largest number that goes into both integers. For example,

Note that

The basis of the algorithm:

• Let \( d \) be a divisor of \( x \) and \( y \)
• compute \( x \mod y \) \[\begin{aligned} x &= yq + r &&\text{where } 0 \leq r \leq y \end{aligned}\] \( x \) is a multiple of \( d \) , and \( yq \) is also a multiple of \( d \) . Since this is an equality, \( r \) must also be a multiple of \( d \) .
• So if \( d | x \) and \( d | y \) then, \( d | r \) .

The algorithm in its recursive form is defined as

Our basecase for implementation will be the previously given \( \text{GCD} (0, x) = x \) .

It can also be implemented using a loop:

gcd(x, y):
    while y != 0:
        t = y
        y = x % y
        x = y
    return x

Recall that we want our algorithms to run in a logarithmic time (time relative to the amount of bits to represent the number).

Theorem: \( \text{GCD} (x,y) \) is \( O(\log(\max(x,y))) \) .

A lemma:

If \( a > b \) , then \( a \mod b < \frac{a}{2} \) .

Case when \(b \leq \frac{a}{2}\): \[ a \mod b < b \leq \frac{a}{2} \]

Case when \(b > \frac{a}{2}\): \[ a \mod b < \frac{a}{2} \]

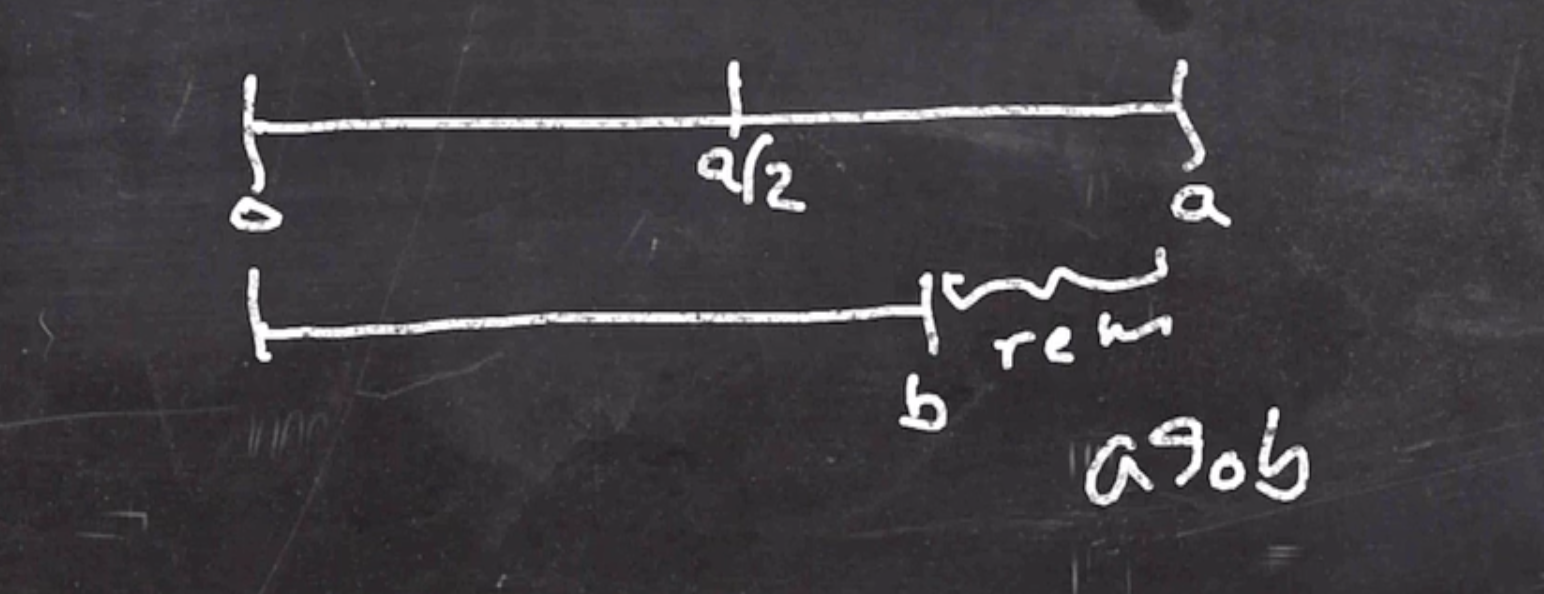
So on each mod, the numbers are swapped and the bigger number is cut in at least half. So we have a logarithmic number of iterations to reach the result.

Examples #

Extended Euclidean algorithm #

For example

Note that

Multiplicative inverses #

We can use our GCD algorithms from before to find the inverse of a value.

Lets say we’re looking for the inverse of \( 5 \mod 31 \) , if use the extended GCD algorithm we’ll get back a linear combination.

So \( 5b \mod 31 = 1 \) means \( b \) is the inverse of \( 5 \mod 31 \) .

Note that if \( b < 0 \) , we add \( 31 \) to it until positive.

Example 1 #

Lets actually find the multiplicative inverse of \( 5 \mod 31 \) :

So since \( b \) is negative, we add to it until its positive

So

Example 2 #

Lets find the multiplicative inverse of \( 7 \mod 31 \) :

As soon as we have the number 1 as a linear combination of our original numbers, ie

we can find the inverse.

So our multiplicative inverse of \( 7 \mod 31 \) is \( 9 \) .