Course orientation #
Syllabus #
152-syllabus.pdf
Notes during orientation #
- Programming will be required in each module, programming intensive
- Brush up on probability of simple events, simple conditional events
- Shallow introduction into groups and fields
- Class is only 5 weeks and 2 days long, so extremely accelerated, at least 20 hrs/week needed
- Hybrid class, half videos posted, and half live.
- Class will start at 1, and go until lecture finishes, then unrecorded open office hour
- 5 modules, starts on thursdays
- Permutation functions and C programming
- Symmetric encryption
- Hashing and authentication
- Asymmetric cryptography and algorithms on large number
- Crytographic systems
- Exams on week 3 and 5
- Group quizzes on tuesdays, in breakout rooms on Zoom
- Last day is comprehensive final
- Take all assignments seriously, nothing is dropped
Brief introduction to cryptography #
Communication in the presence of adversaries
Ron Rivest
If Alice and Bob want to communicate, the have some kind of medium (like a network connection, or any for of communication).

In the midst of the communication medium, there is Eve, the adversary. Eve can passively attack: reading all the messages that go back and forth. Our adversary can also do active attacks: modifying the messages, inserting messages, or delete messages.
So we must imagine that our adversary is very powerful. If you can secure your communications in the presence of a powerful adversary, then they will also be secure for the weaker.
Eve also has Kerckhoff’s law: the adversary knows everything except secret keys. We must assume Eve knows the algorithms being used in the cryptographic process.
Note: Keys in cryptography refers to a random string of bits.
Two kinds of cryptography #
Symmetric:
- Alice and Bob share the same secret key
- Much faster (thousands of times faster)
Asymmetric:
- Alice and Bob each have their own secret key
- Scales better, easier to manage keys among large groups. Linear as opposed to symmetric’s exponential key count.
- More flexible, no trust needed to establish secure connection.
What happens in the real world: hybrid cryptography #
This is a combination of symmetric and asymmetric cryptography.
- Use asymmetric cryptography to start the communication
- Establish a shared secret
- Switch to symmetric for the rest of the communication
Two main goals #
Secrecy
- Adversary should not extract any information
- Verb used: encrypt/decrypt
Authentication
- Receiver is able to verify the data is unaltered and from the sender
- Verb used: authenticate, sometimes called MACing (message authentication code)
- In asymmetric: signature
- In symmetric: MAC
Review of older topics #
Functions and permutations #
Cryptography is largely based on invertible functions. We also need to understand some probability distributions used in cryptography.
For example:
“Let \( f:Z_5 \to Z_4 \) be a function …”
Here
- \( f \) is the name of the function
- \( Z_5 \) is the domain
- \( Z_4 \) is the codomain
- The fact that its a function means that every domain element is mapped to 1 codomain element.
Note: We will define \( Z_n = \{0,1,2,\ldots,n-1\} \)
We will only consider discrete functions in this class.
Two ways to think of a discrete function #
Consider the function \( f: Z_5 \to Z_4 \)
Arrow diagrams
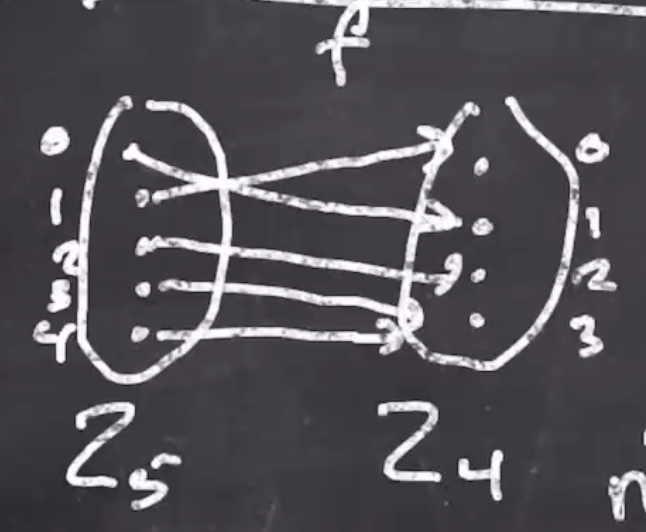
- Every domain element has exactly 1 arrow to the codomain.
- A function is onto if each codomain element has at least 1 arrow to it.
- A function is 1-to-1 if each codomain element maps has less than or equal to 1 arrow to it.
- The inverse of the function is if you reverse the arrows. Only functions that are onto and 1-to-1 are invertible. If we reverse the arrows of the above function, we can tell the inverse is not a function (multiple arrows coming out of one element).
Tables
| \( x \) | \( f(x) \) |
|---|---|
| 0 | 1 |
| 1 | 0 |
| 2 | 2 |
| 3 | 3 |
| 4 | 3 |
If this is a function:
- Each domain element appears exactly once in the first column and each element in the second column is in codomain
- For a function to be onto: each codomain element appears in the second column
- For a function to be 1-to-1: no repeats in the second column
- Invertible if both of the above are true: each codomain elements appears exactly once in the second column, we can see the function is not invertible because 3 appears twice in the second column
Definition: a function is invertible if and only if it is 1-to-1 and onto.
A invertible function’s domain and codomain will be sets of the same size.
Random functions #
A random function is one where each element of the codomain (second column) is chosen uniformly at random.
So if we say “let \( f: Z_5 \to Z_4 \) be random …”, imagine that we have a table defining \( f \) where the second column is randomly picked using a random probability (like a coin flip).
| \( x \) | \( f(x) \) |
|---|---|
| 0 | 3 |
| 1 | 3 |
| 2 | 2 |
| 3 | 2 |
| 4 | 3 |
Random functions are defined randomly, but are then fixed. So multiple calls to \( f(0) \) will always return \( 3 \) .
Sometimes its useful to be lazy when defining a random function, that is to generate the output only on the first call to the input.
Examples #
What is the probability that \( \left[ f(1) = 2 \mid f(0) = 2 \right] \) ?
If we are filling the table lazily, the probability is \( \frac{1}{4} \) because the output has not been defined yet.
What is the probabilty that \( \left[ f(1) = 2 \mid f(1) = 1 \right] \) ?
This is \( 0 \) , because the output has already been defined.
Permutations #
File: Permutations functions
A permutation function is an invertible function where the domain = codomain.
For example we might say “let \( p: Z_4 \to Z_4 \) be a random permutation function …”
| \( x \) | \( p(x) \) |
|---|---|
| 0 | 1 |
| 1 | 3 |
| 2 | 0 |
| 3 | 2 |
Note: the second column above cannot have any repeats because it is invertible.
The first output generated is uniformly distributed (because nothing is in the table at the beginning).
Probability #
Let \( p: Z_4 \to Z_4 \) be a random permutation function. We will use a lazy output table generation:
What is \( P(p(1) = 2 \mid p(0) = 1) \) ?
Answer: \( \frac{1}{3} \)
What is \( P(p(1) = 1 \mid p(0) = 1) \) ?
Answer: \( 0 \)
C memory models #
A allocated chunk of memory can be represented by a long rectangle, which could be filled by a network or a file read etc:

Left end is the address of the first byte (pointer). The span of the rectangle is the amount of memory allocated (the length).
Cryptographic functions will be given a buffer like this, and will manipulate the data in the buffer.
A C programming interface #
Lets say we have
void foo(void * p, int nbytes)
We use a void pointer void * to avoid type warnings.
It is a memory address with no associated type.
Another interface may be:
#include <stdint.h>
void foo(uint8_t * p, int nbytes);
uintN_t, where N is either 8, 16, 32, or 64, each being N bits, can be used to specify the size needed.
uint8_t is the exact same as char, both being the smallest addressable unit (1 byte).
Accessing memory in C #

We can access memory randomly via array subscript notation:
p[i]being theith element. We cannot do this on avoid *, because it doesn’t know the size of each element.p + iis the address ofp[i]element, this is pointer arithmetic.
XOR buffer example #
Lets write a function that takes a buffer as input, and returns the XOR of all the bytes.
#include <stdio.h>
#include <stdint.h>
uint8_t xor_buf(uint8_t * p, int nbytes)
{
uint8_t acc = 0;
for (int i = 0; i < nbytes; i++)
acc = acc ^ p[i];
return acc;
}
int main()
{
uint8_t buf[4] = {1, 2, 3, 4};
// at this point memory looks like this in hex:
// 01 02 03 04
uint8_t result = xor_buf(buf, 4);
printf("%x\n", result);
return 0;
}
When we run this we get the output:
4
which is the expected output.