NP-completeness #

Hamiltonian cycles #

An example of a problem that cannot be solved in polynomial time.

P and NP #

Terminology #

Reduction #

• should first show that \( P \in NP \)

NP-Hard #

• NP-Hard problems are at least as hard as NP-Complete problems

Why prove NP-completeness? #

NP-Complete Examples #

Reduction examples #

Directed hamiltonian cycle to undirected hamiltonian cycle #

It is easier to go the other way (for any undirected edge, we just make it directed in both directions).

So how do we turn a directed graph into an undirected graph, such that they both either have or have not a hamiltonian cycle?

For each vertex in the directed graph, put 3 vertices in the undirected graph:

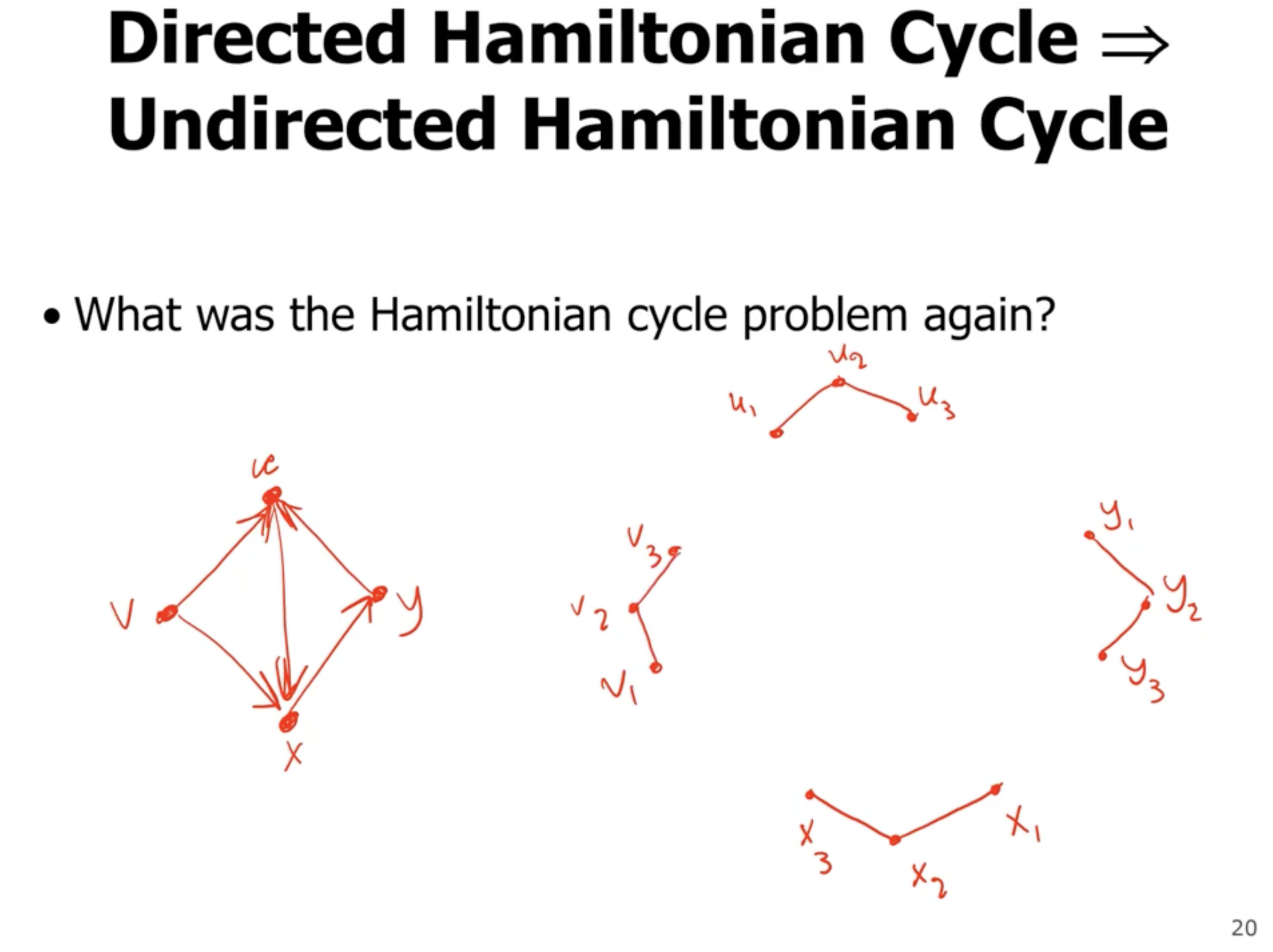
Then, for edges in the directed graph, put an edge from the third vertex to the first in the undirected graph:

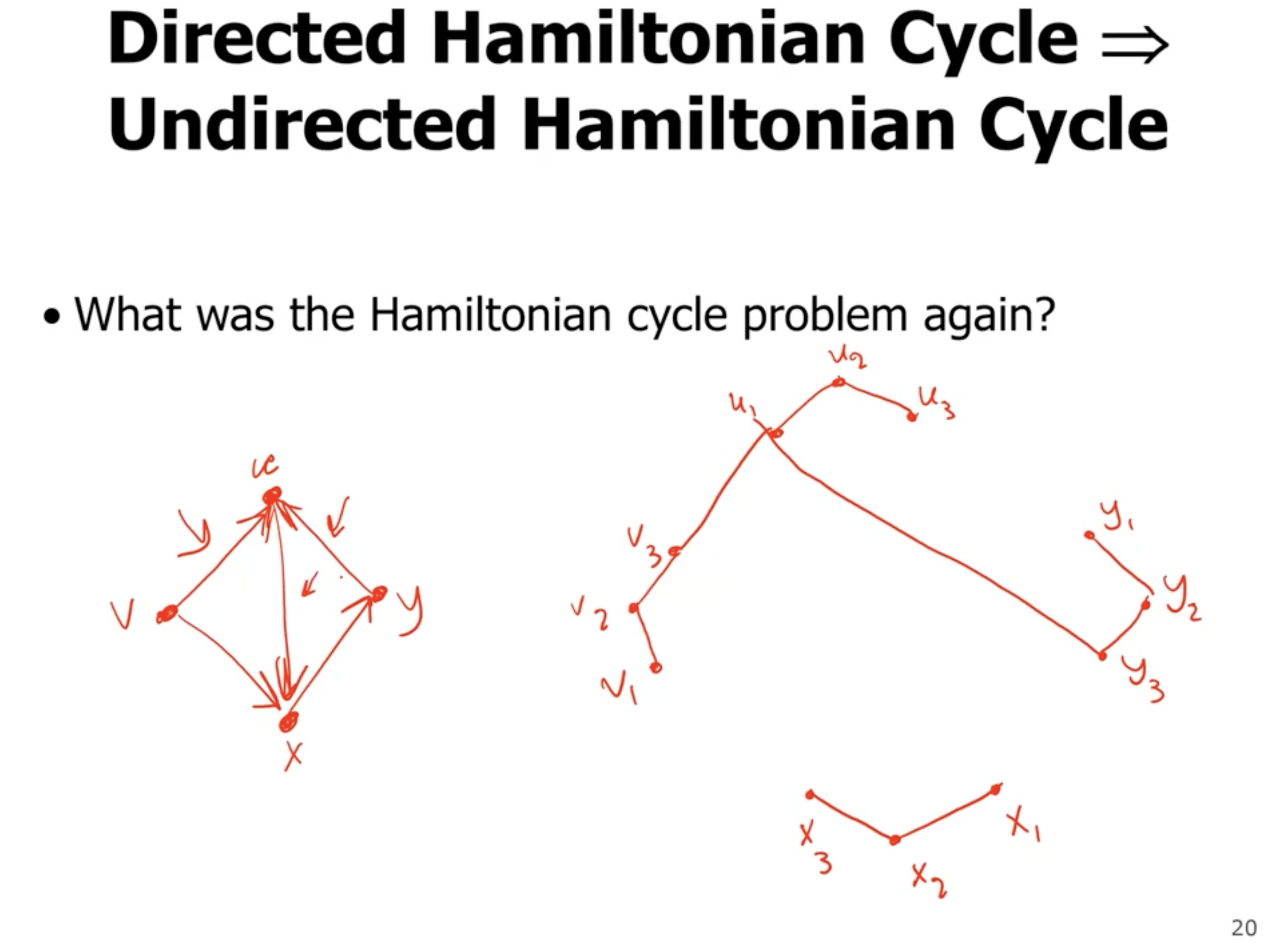
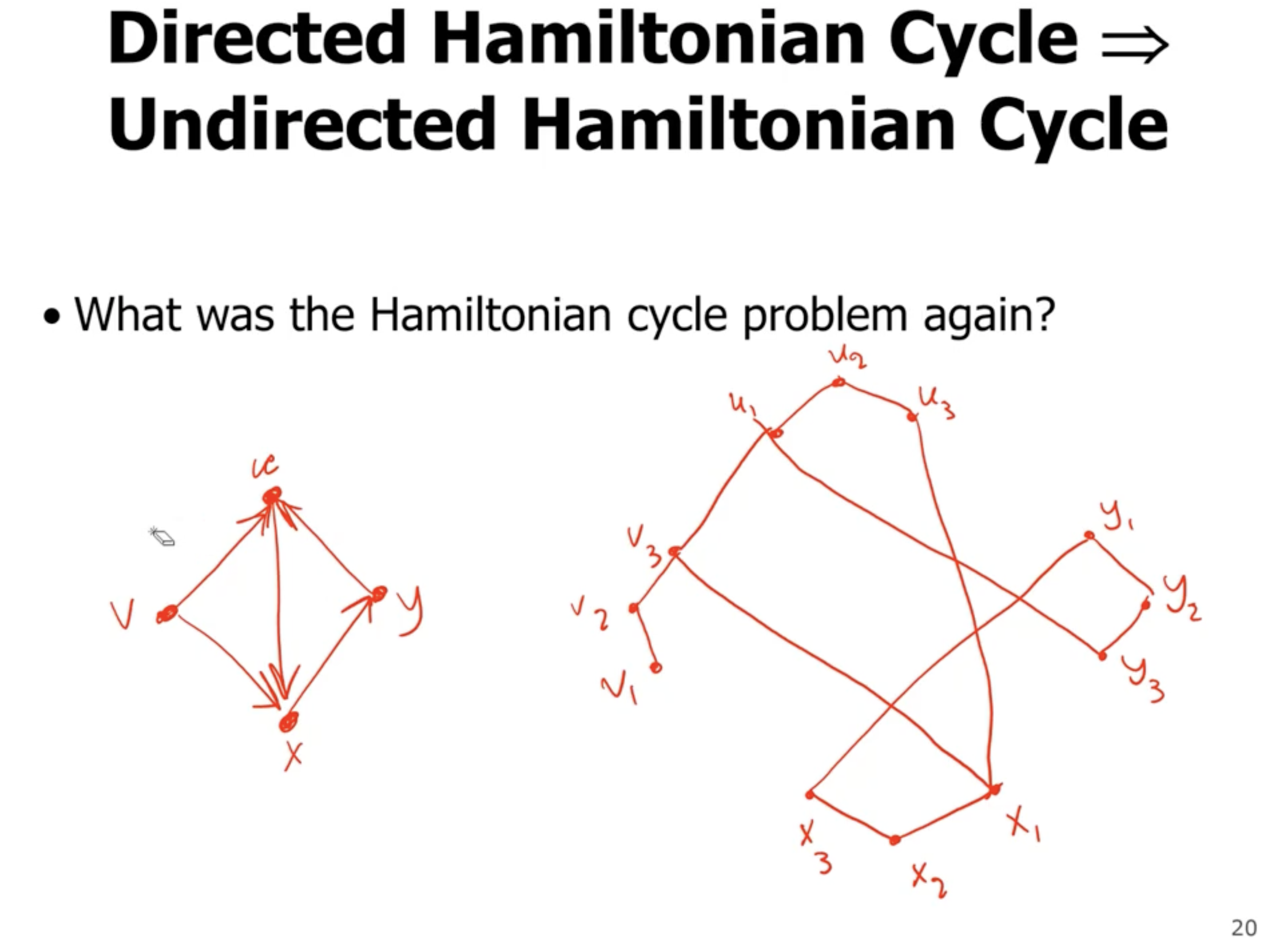
Now, this particular example does not have a hamiltonian cycle, but lets pretend it does (with the darker color):

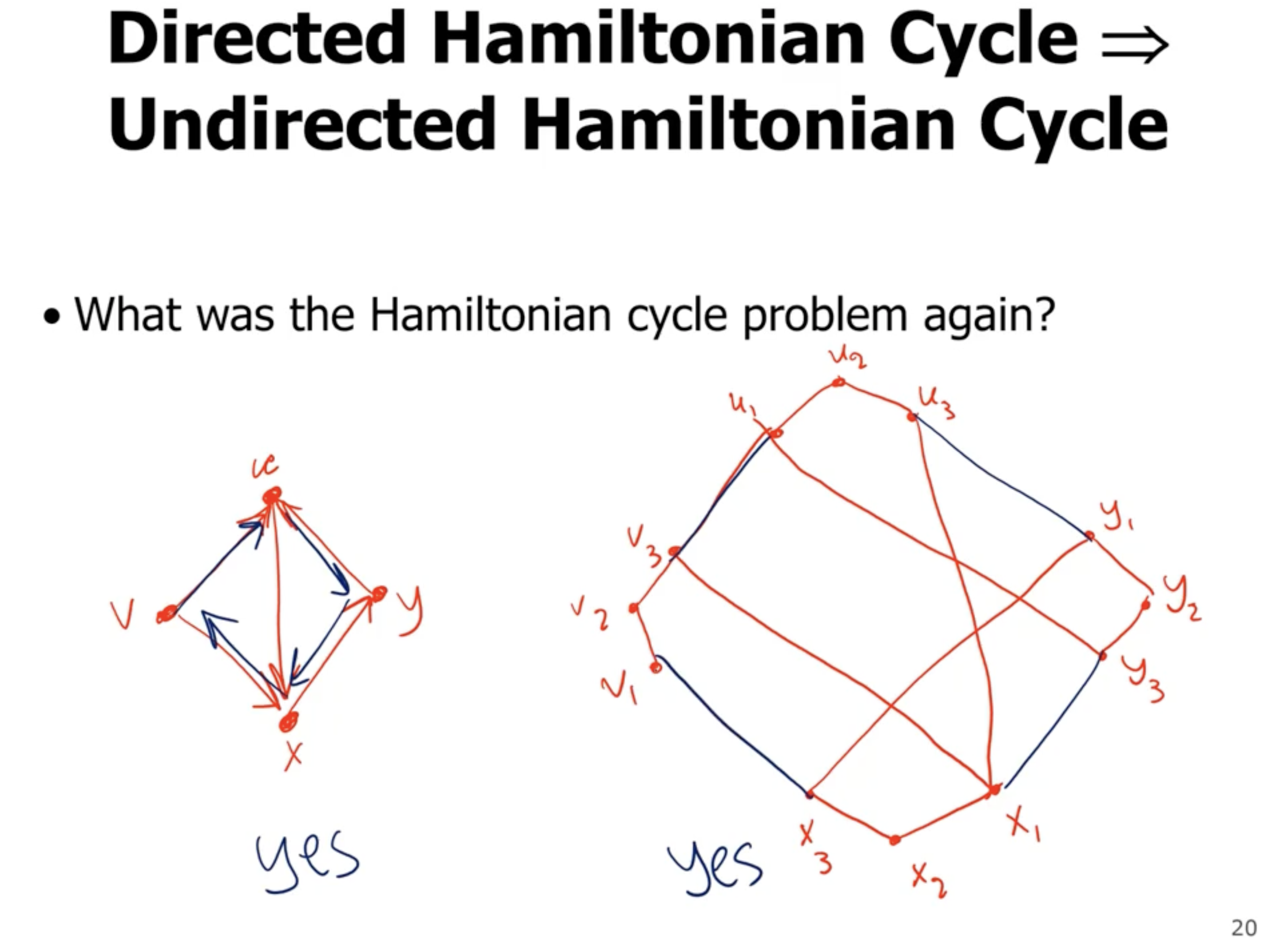
Note that the undirected graph now has the entire perimeter filled in and we can see the hamiltonian cycle.

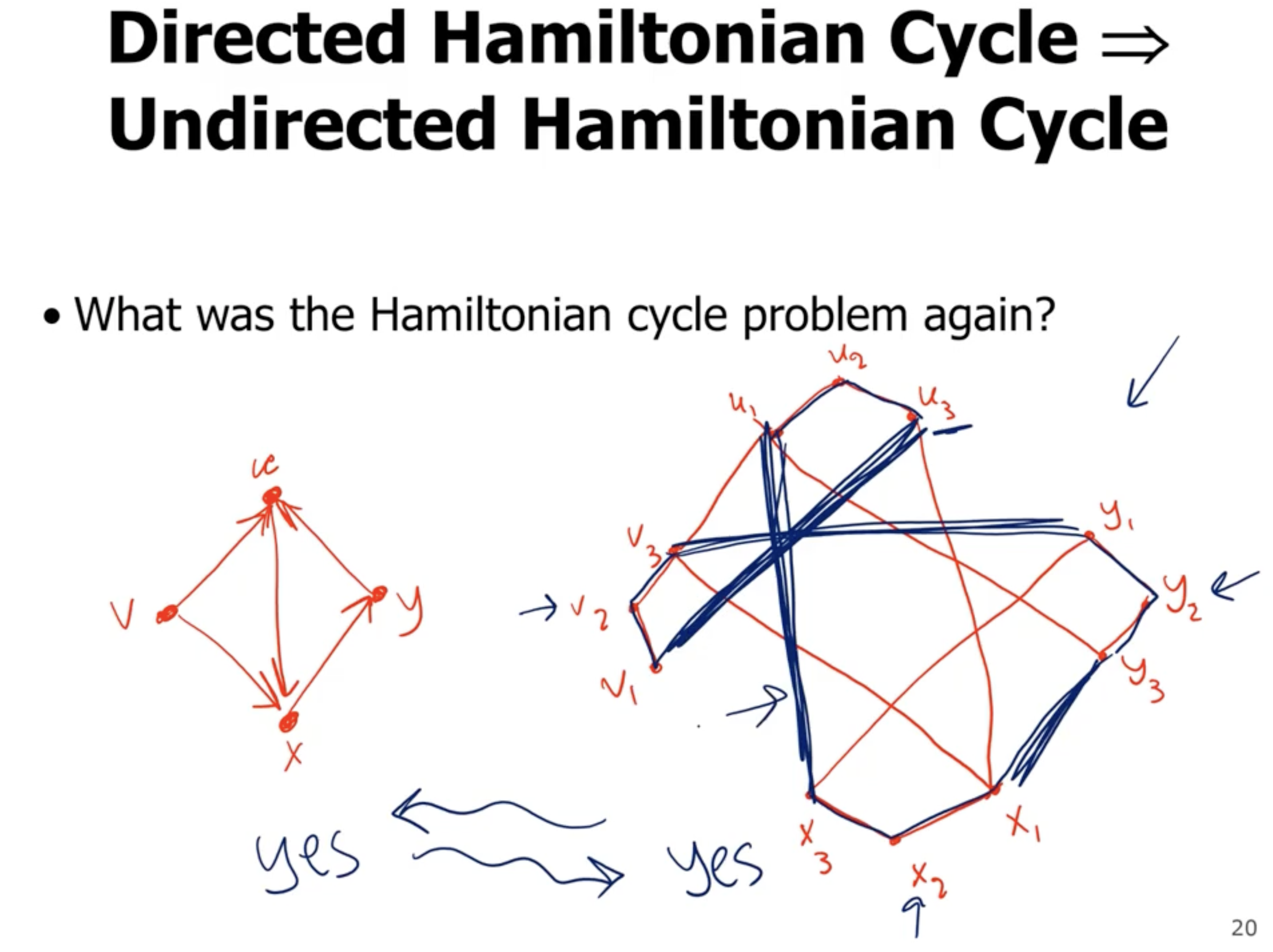
The (bold) edges that go from a third vertice to a first vertice represent a hamiltonian cycle in the directed graph.

The traveling salesman problem #

If we are trying to show that this problem is NP-Complete we need to:

• show that the solution is verifiable in polynomial time
  • with the TSP solution, we can simply sum all of the edges

We can reduce the Hamiltonian cycle problem to a TSP:

If we reduce all edge weights to 1, and the TSP gives a result \( < n + 1 \) , then we have a hamiltonian cycle.