Some more dynamic programming examples #

Segmented least squares #

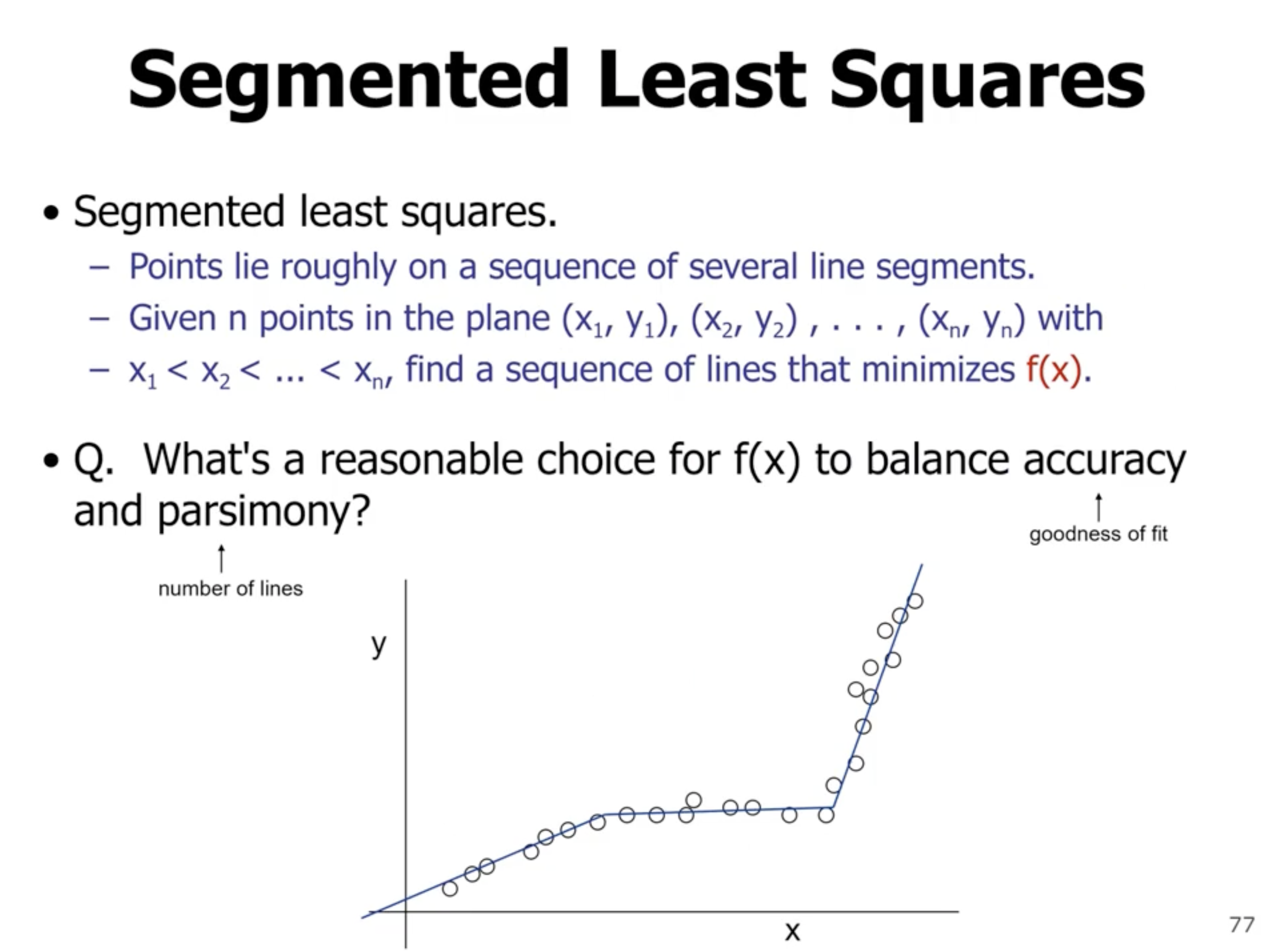
• if we connected all points between each other, there would be zero error
• we want a trade off between accuracy and number of segments

• imagine connecting the last 2 points, and then attaching it to the rest of the optimal solution
• or connecting the last 3 points and attaching it to the rest of the optimal solutions
• and so on…

Weighted activity selection #

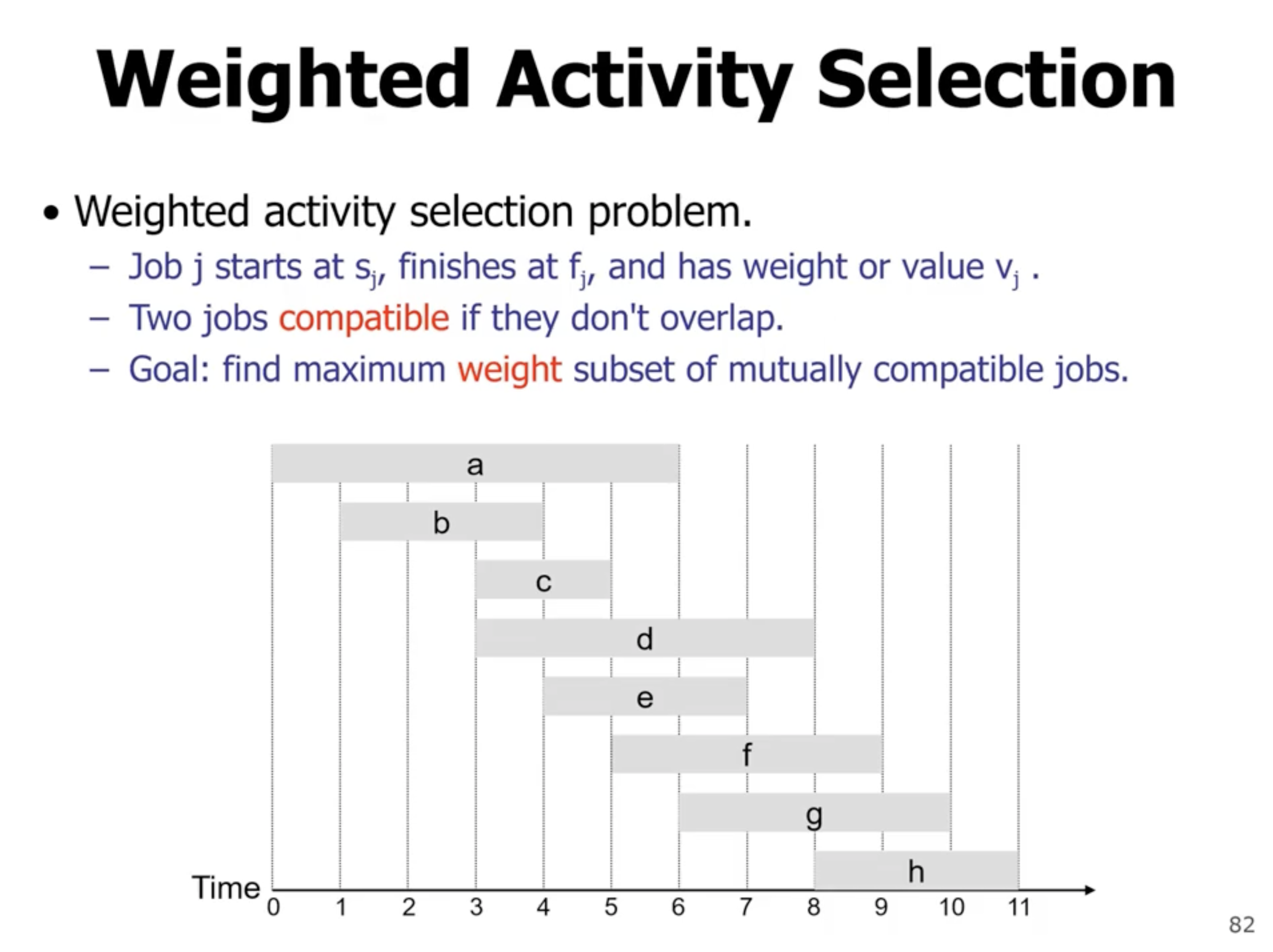
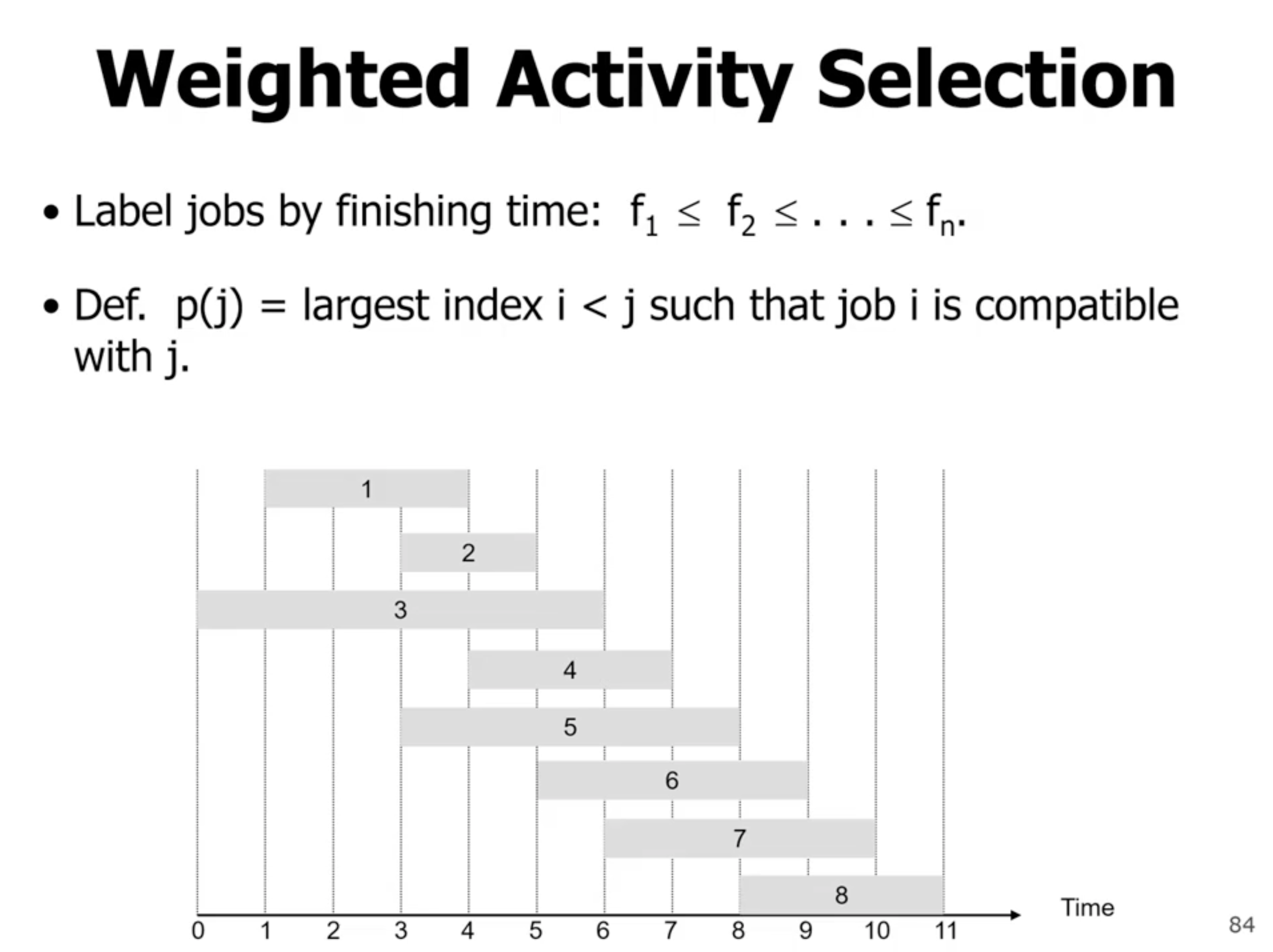
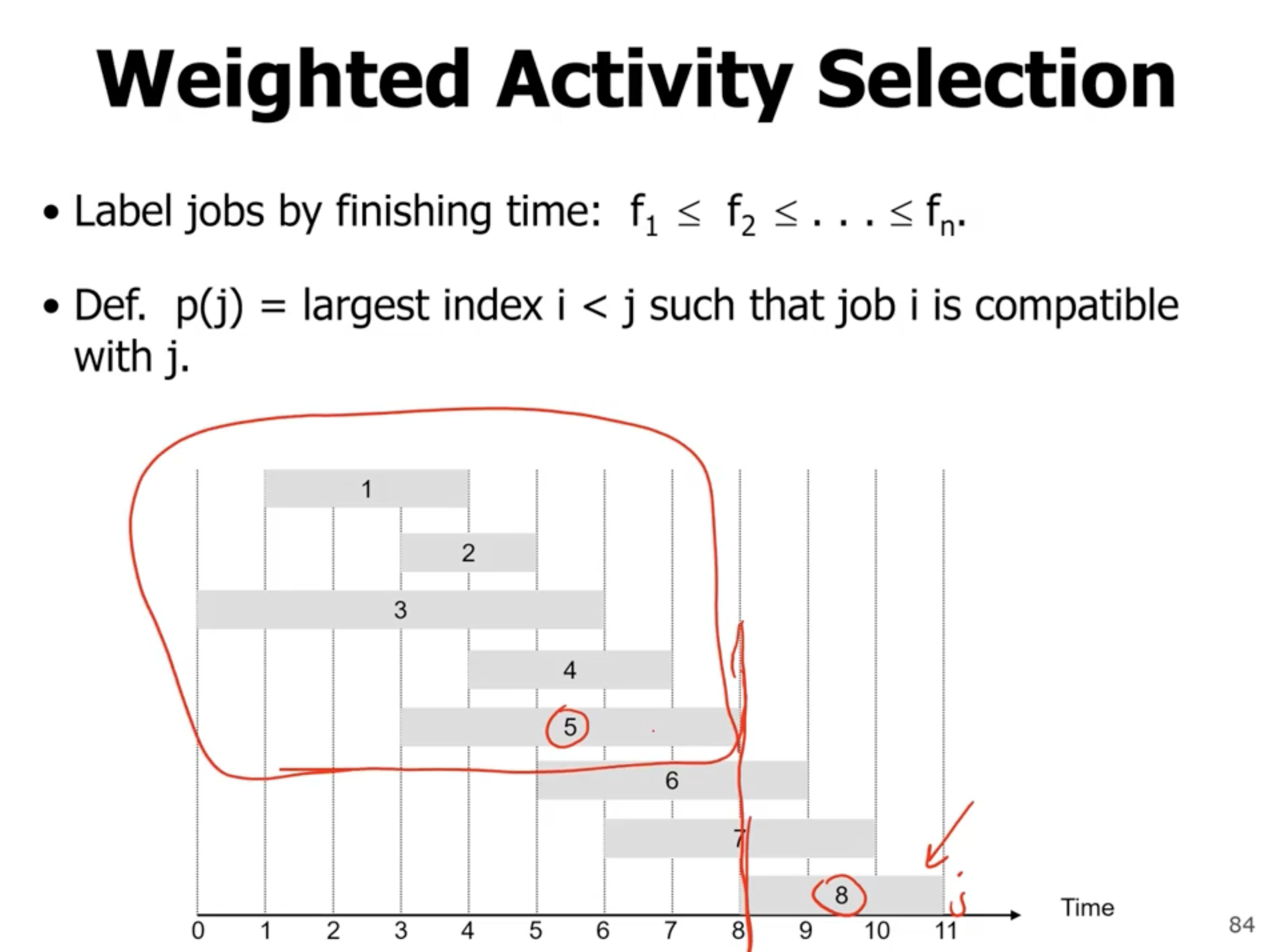
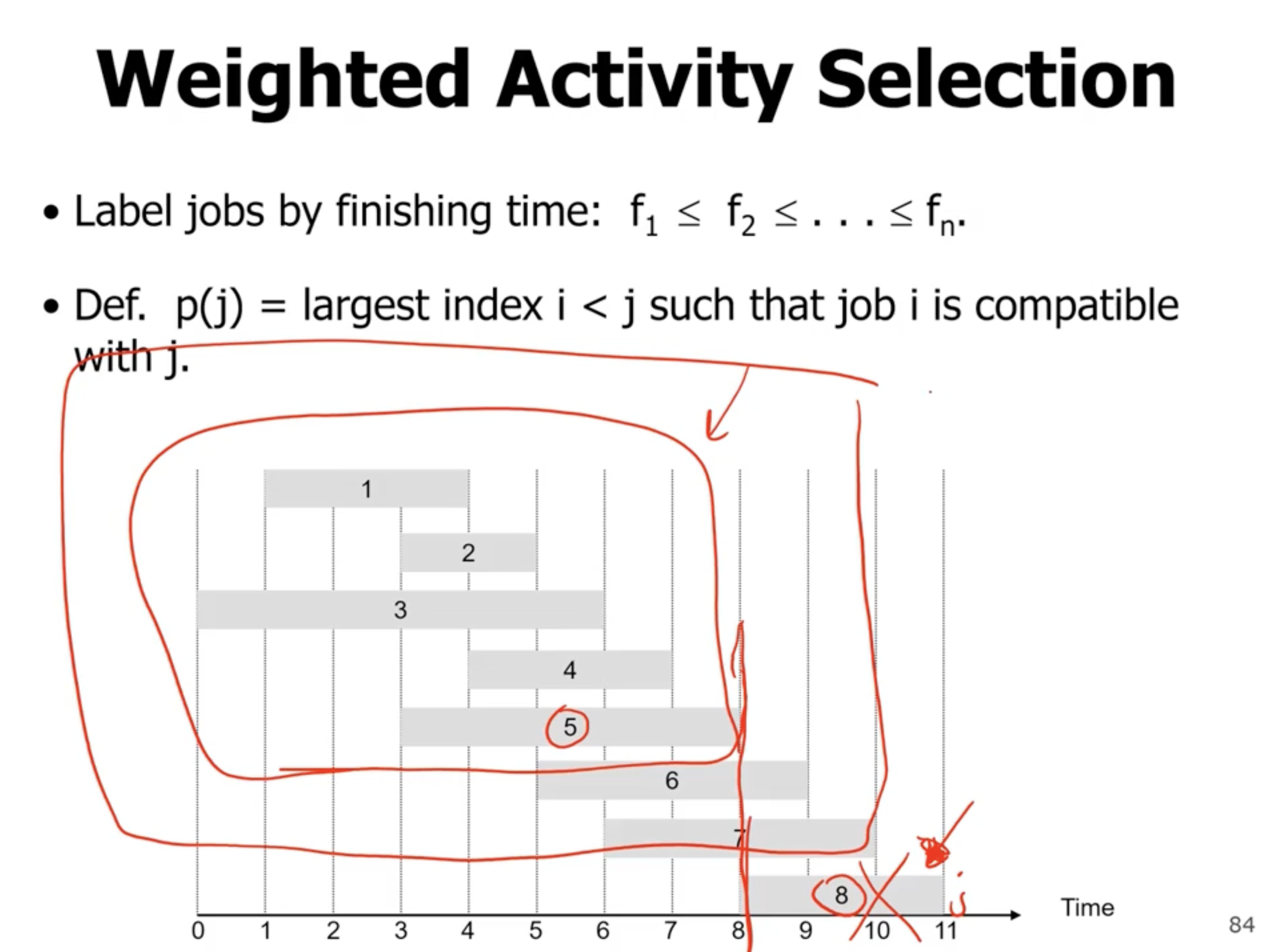
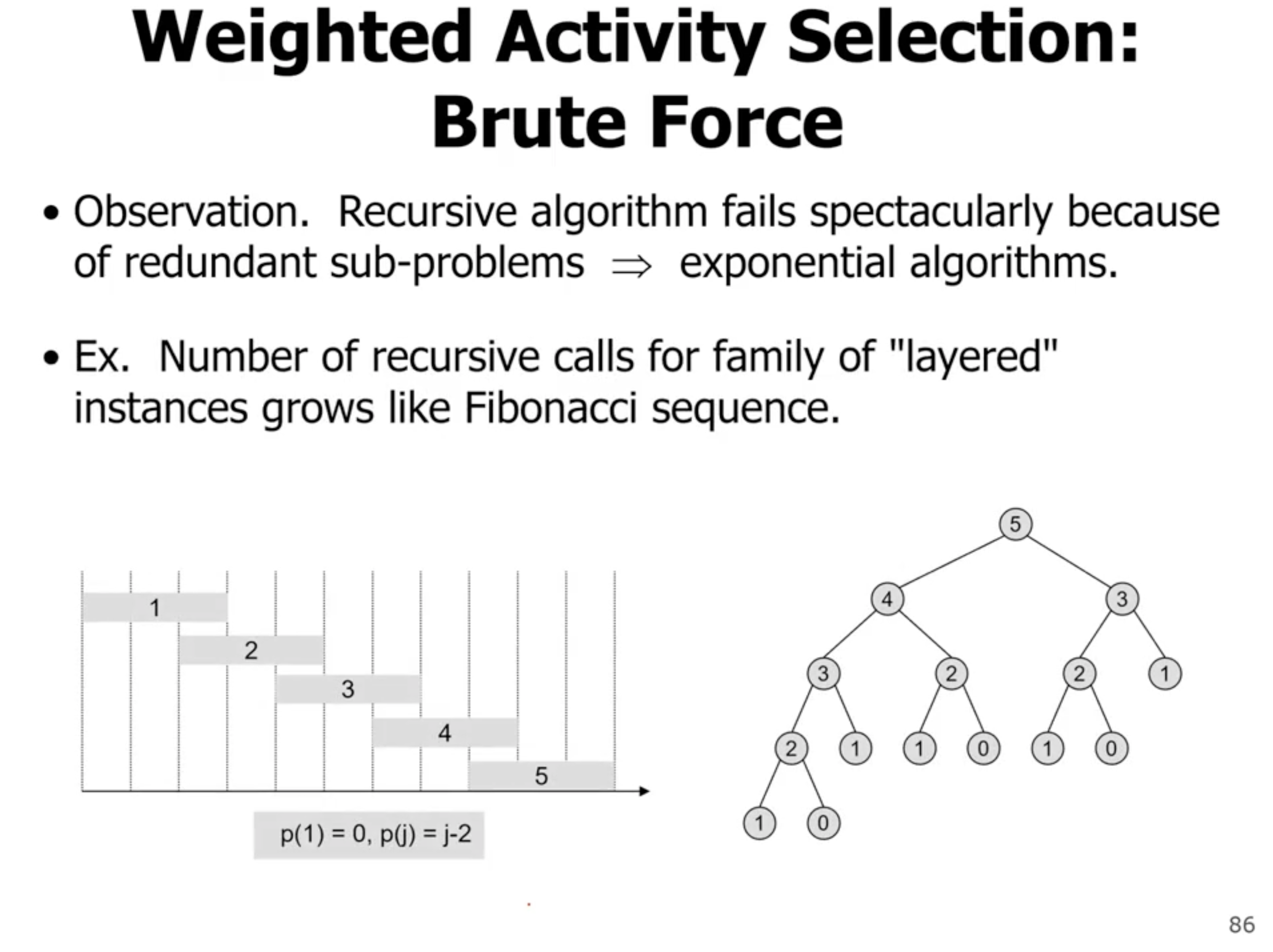
• \( O(n \lg n) \) complexity (sort)

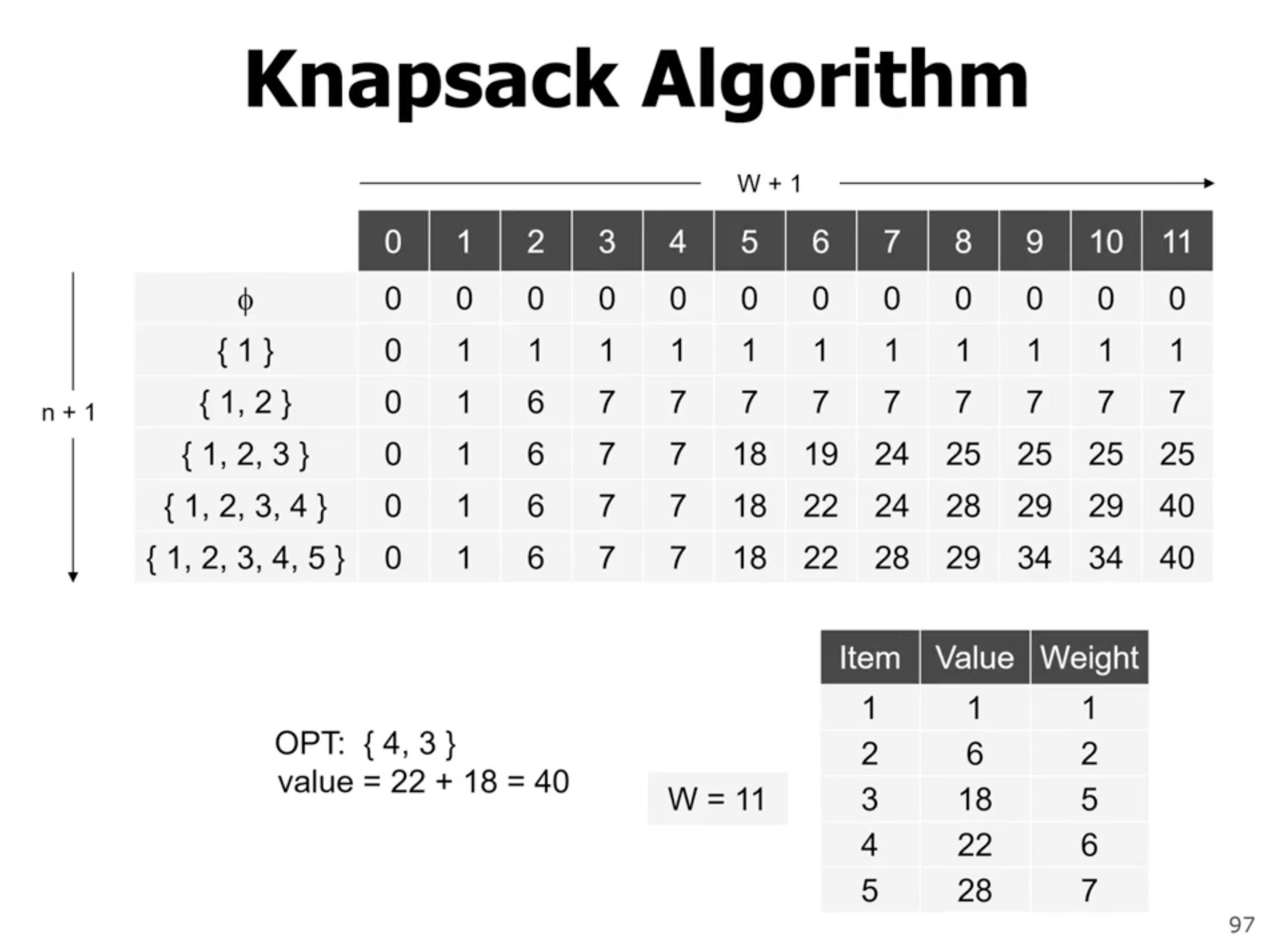
The knapsack problem revisited #

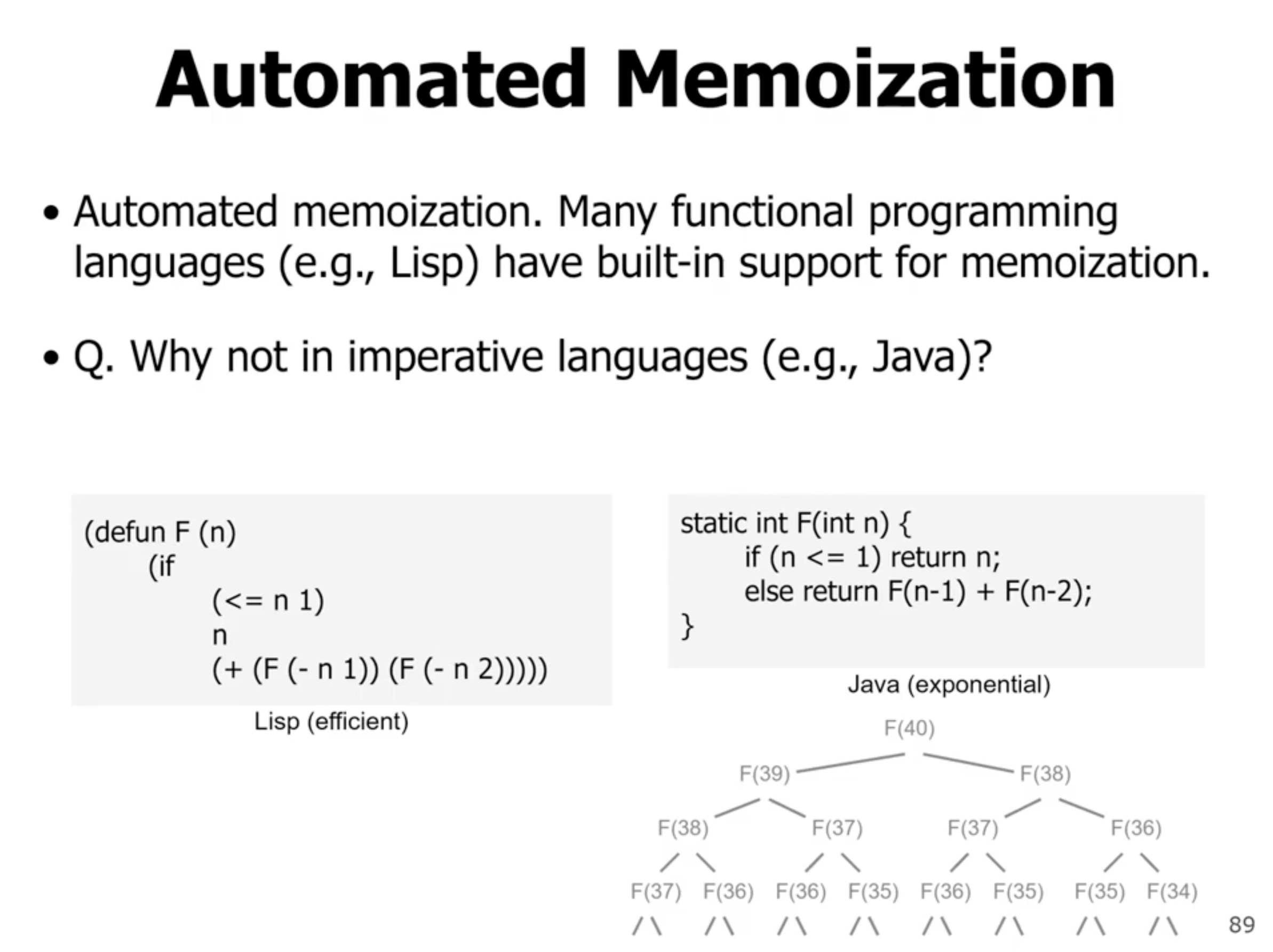
Automated memoization #

Flow network #

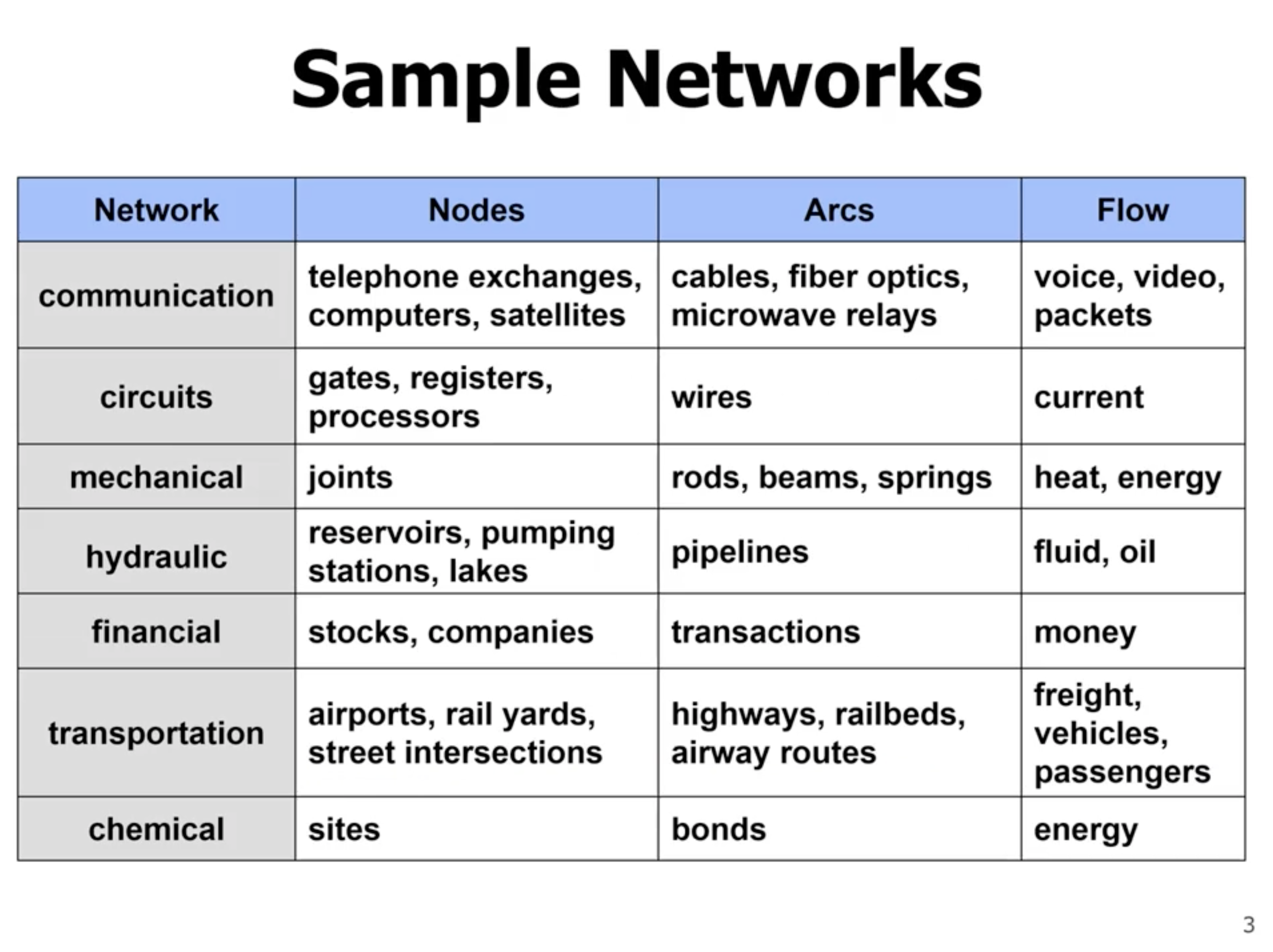
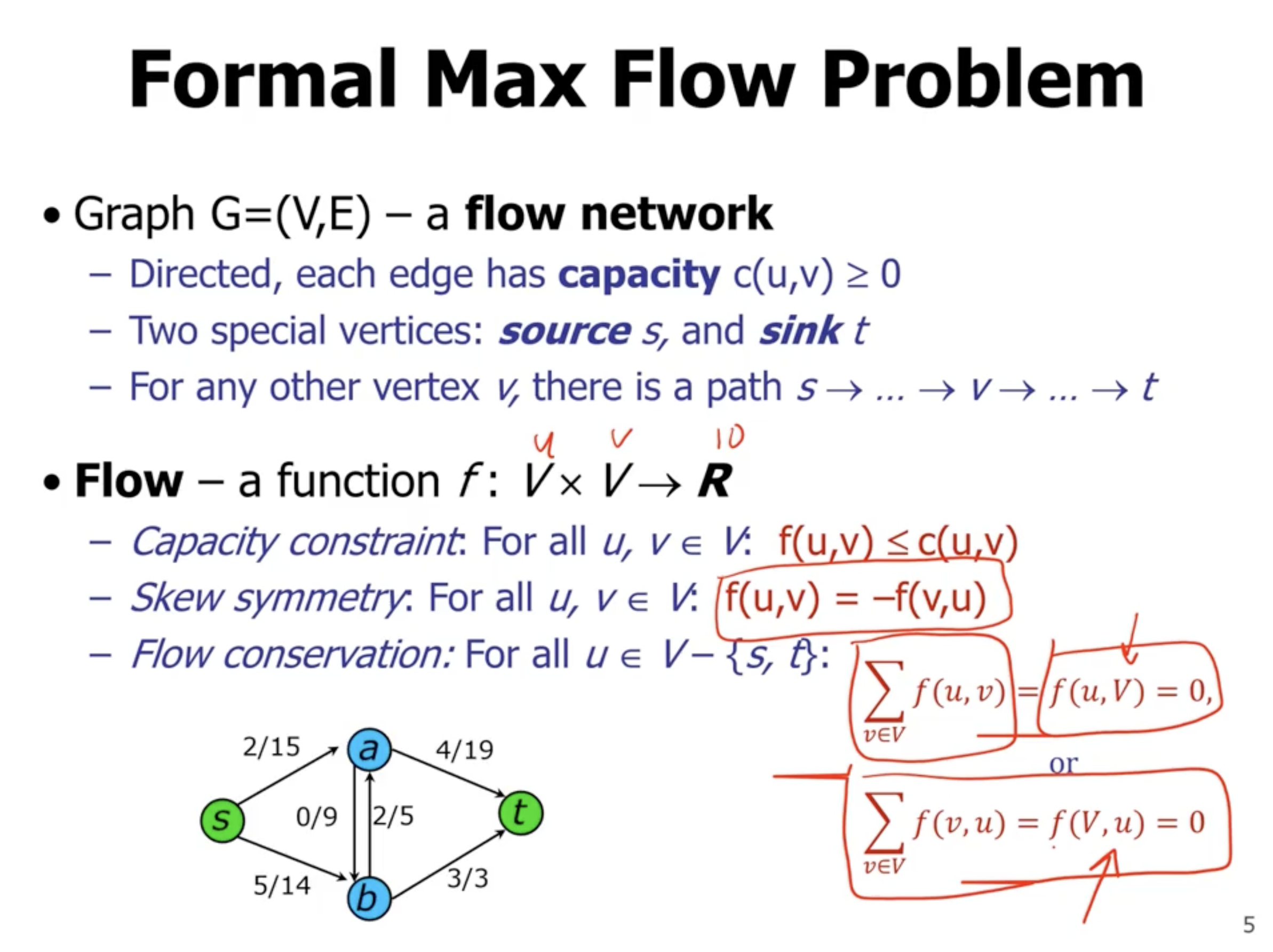
• notation is “capacity / flow”

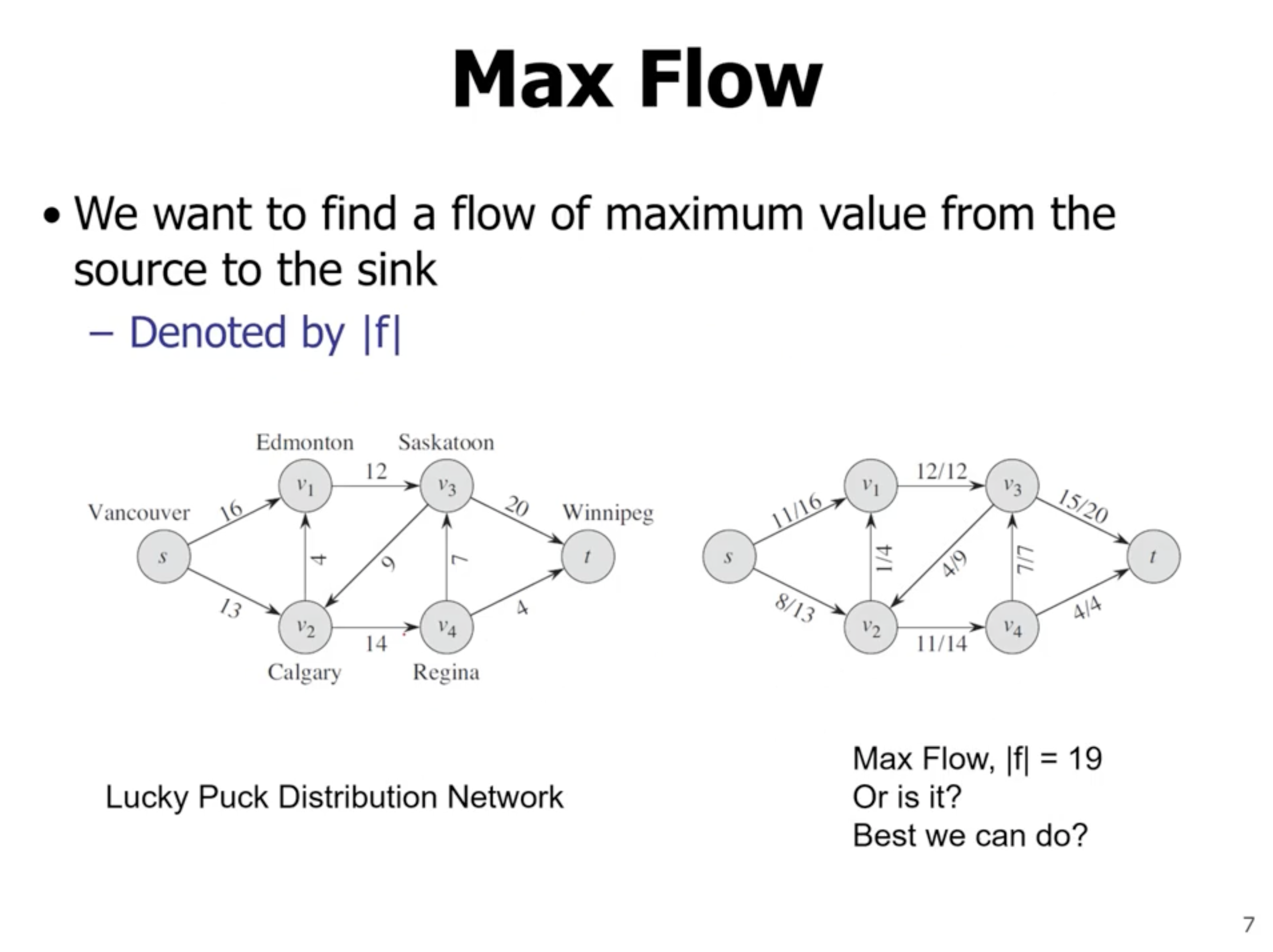
Max flow #

Ford-Fulkerson method #

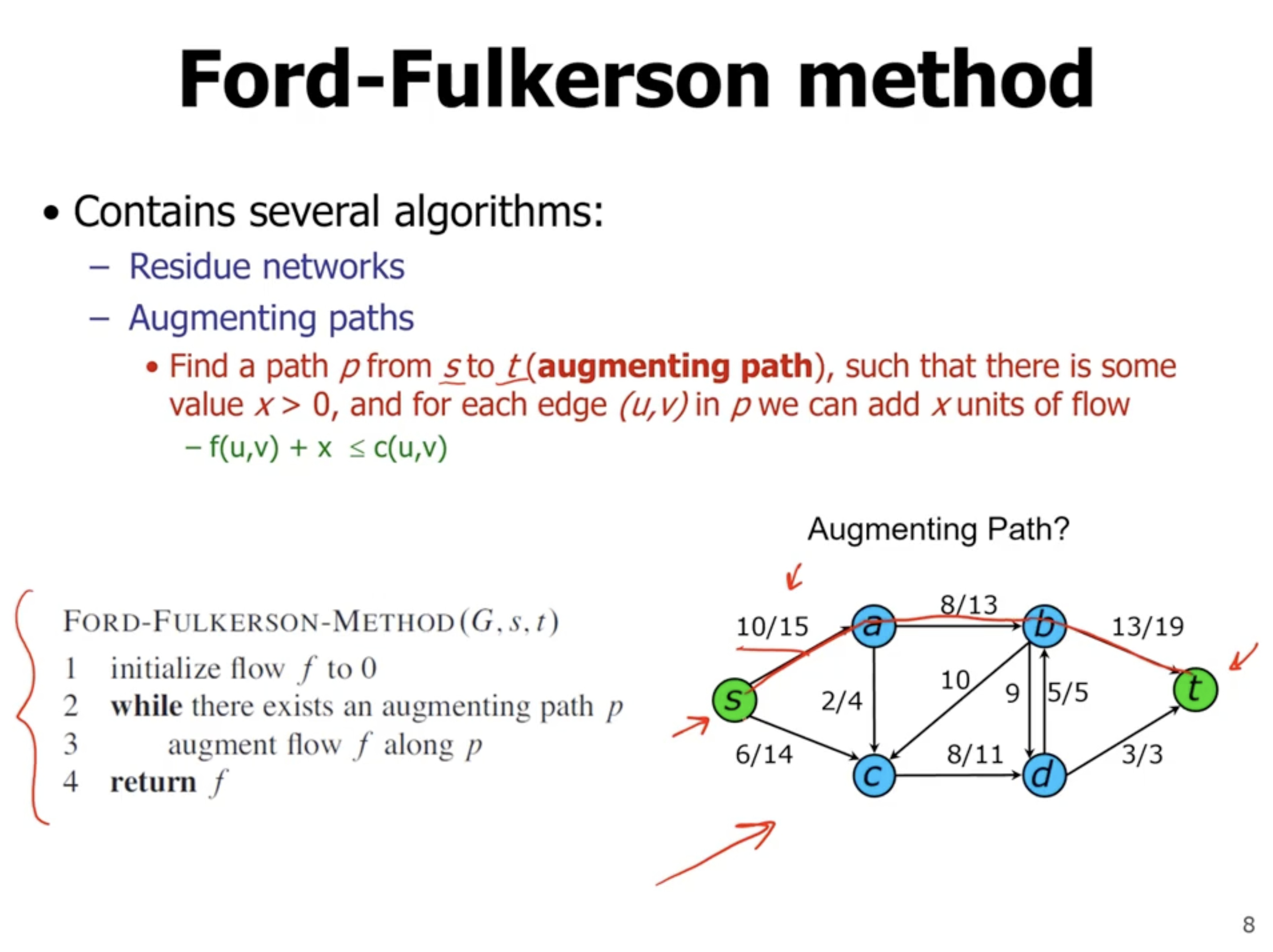
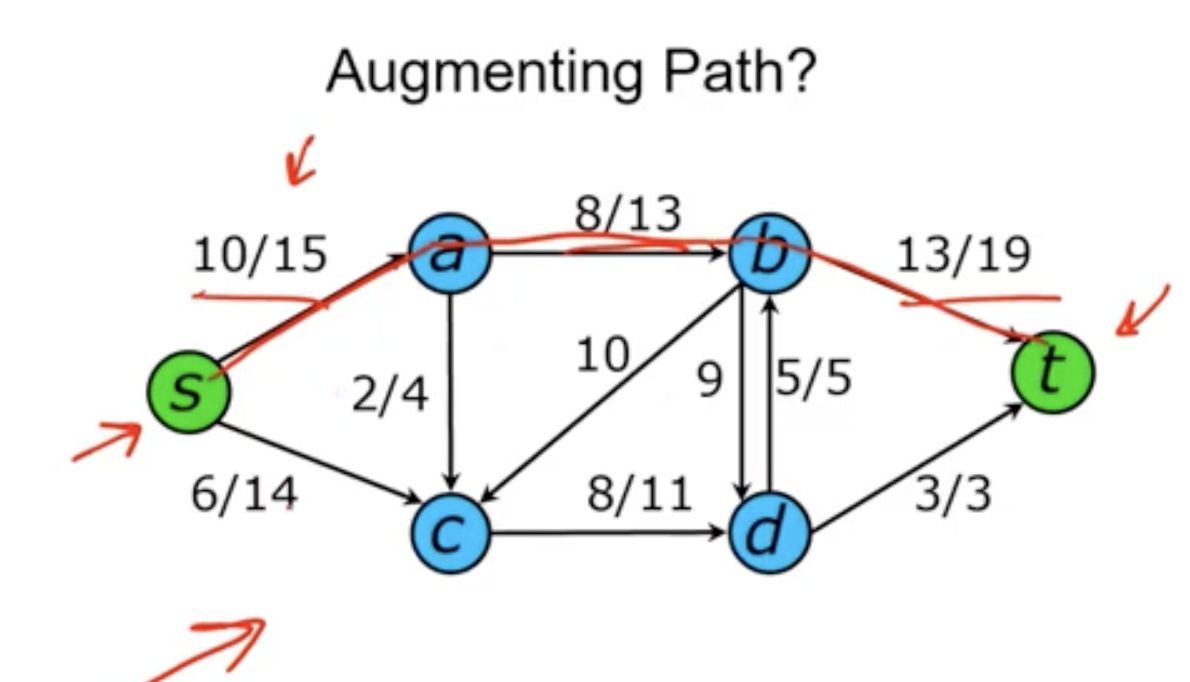
• can increase flow by 5

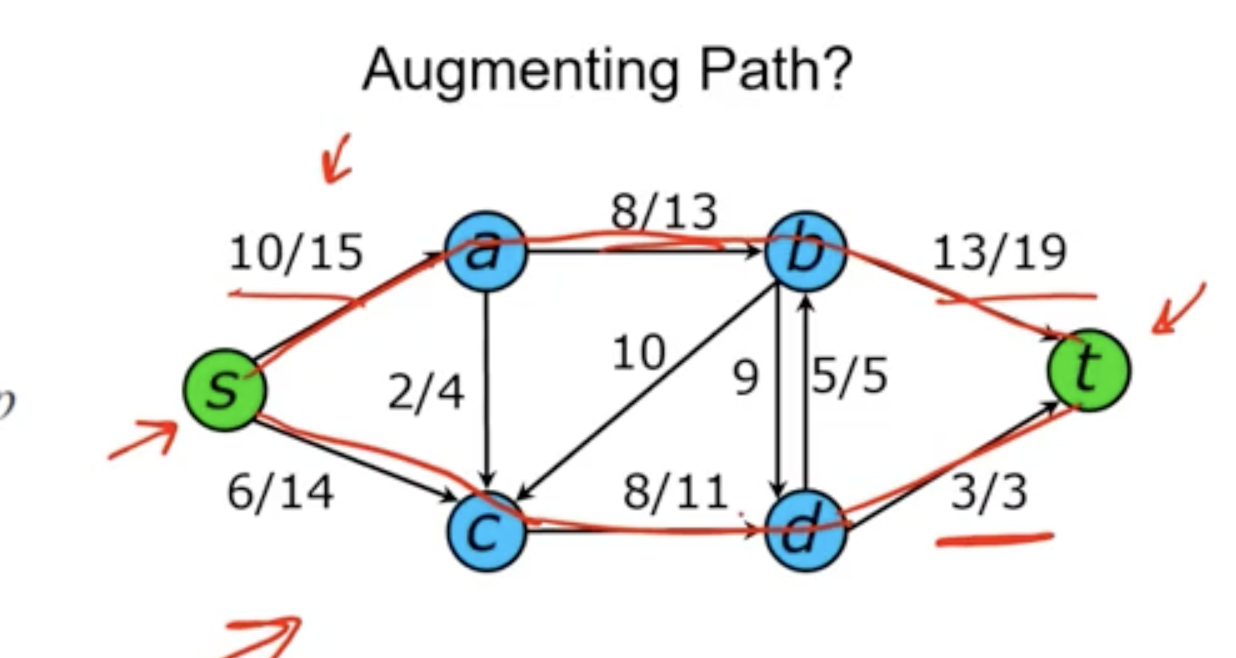
• lower path is not an augmenting edge, flow cannot increase

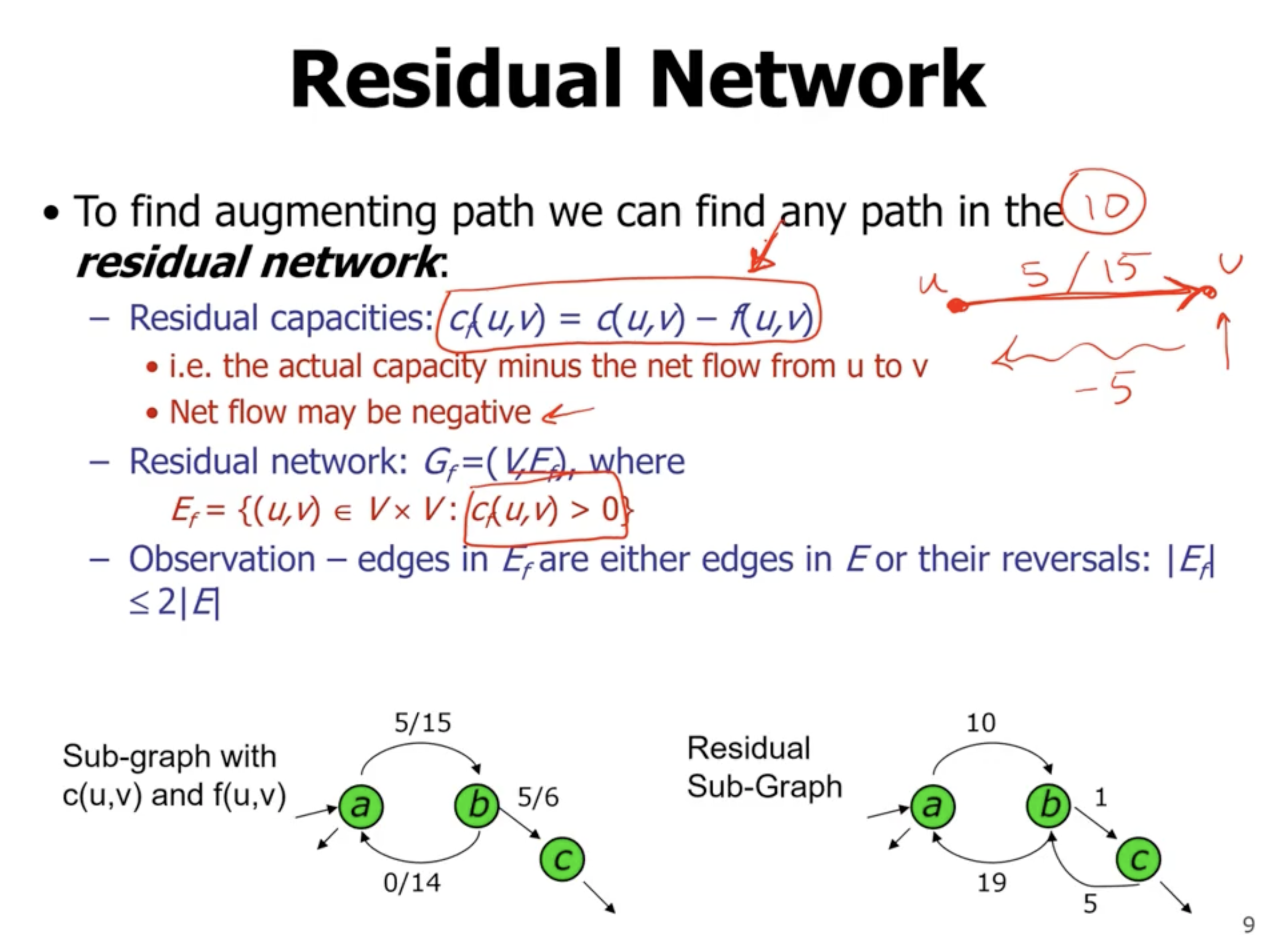
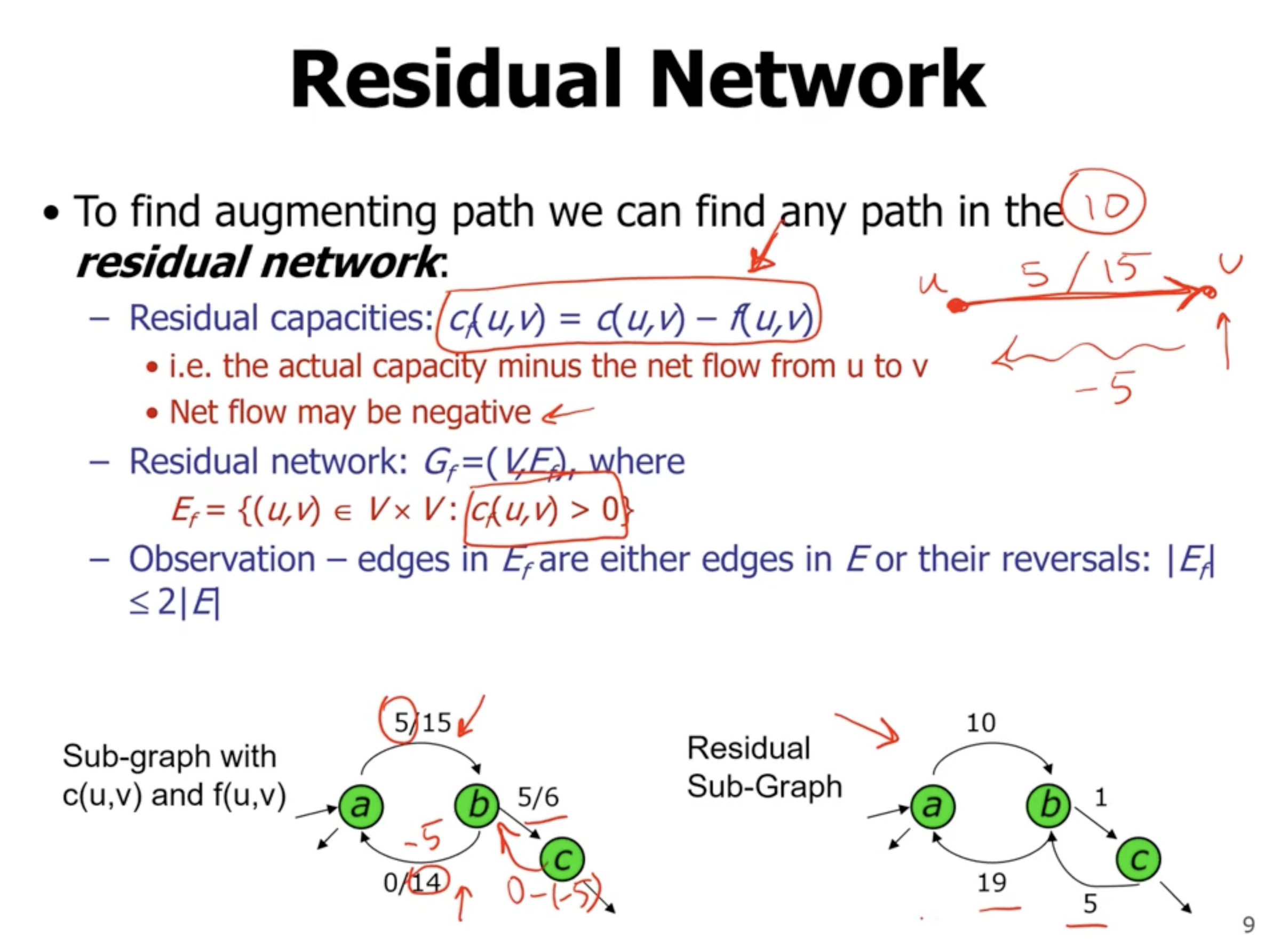
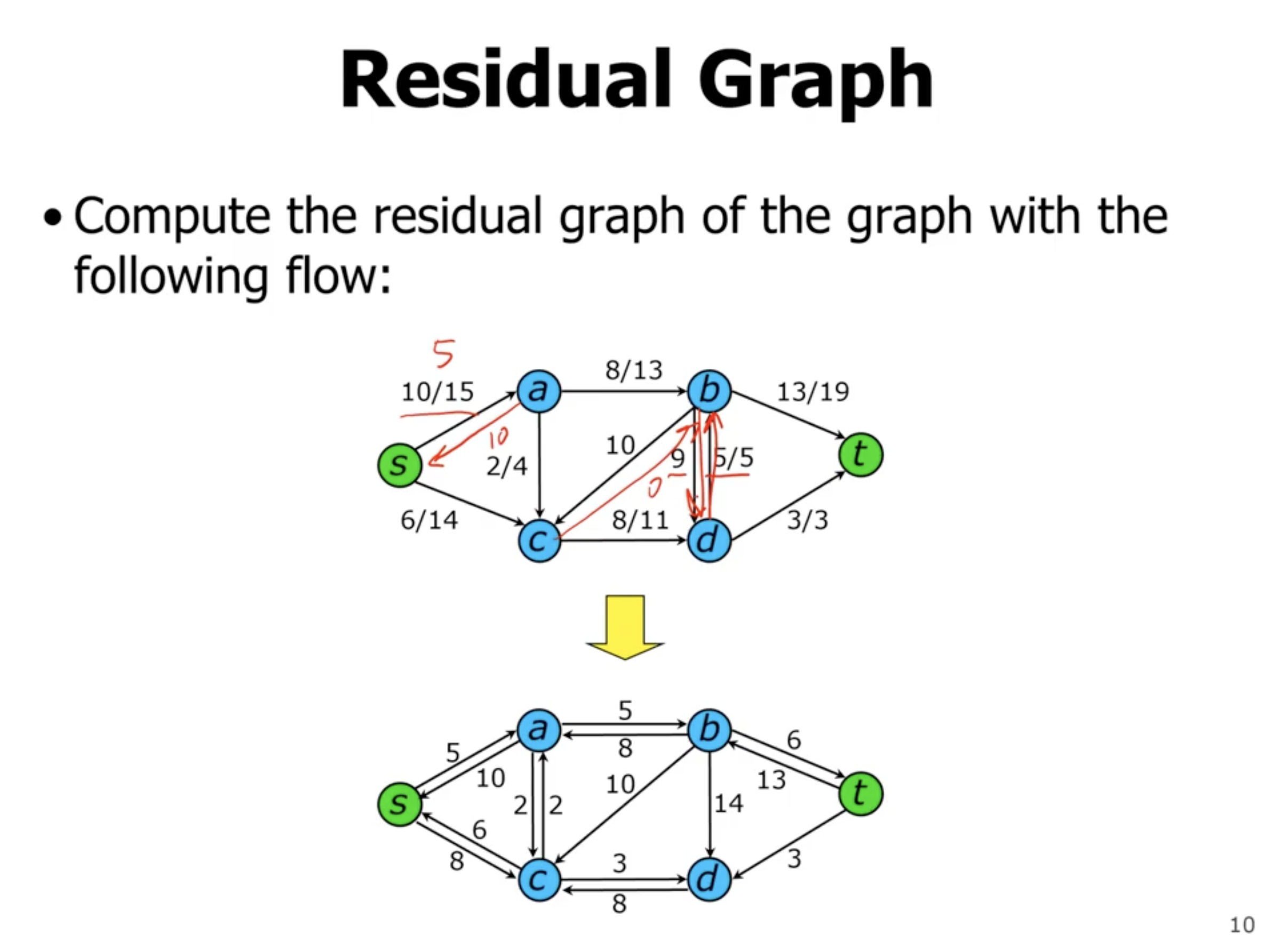
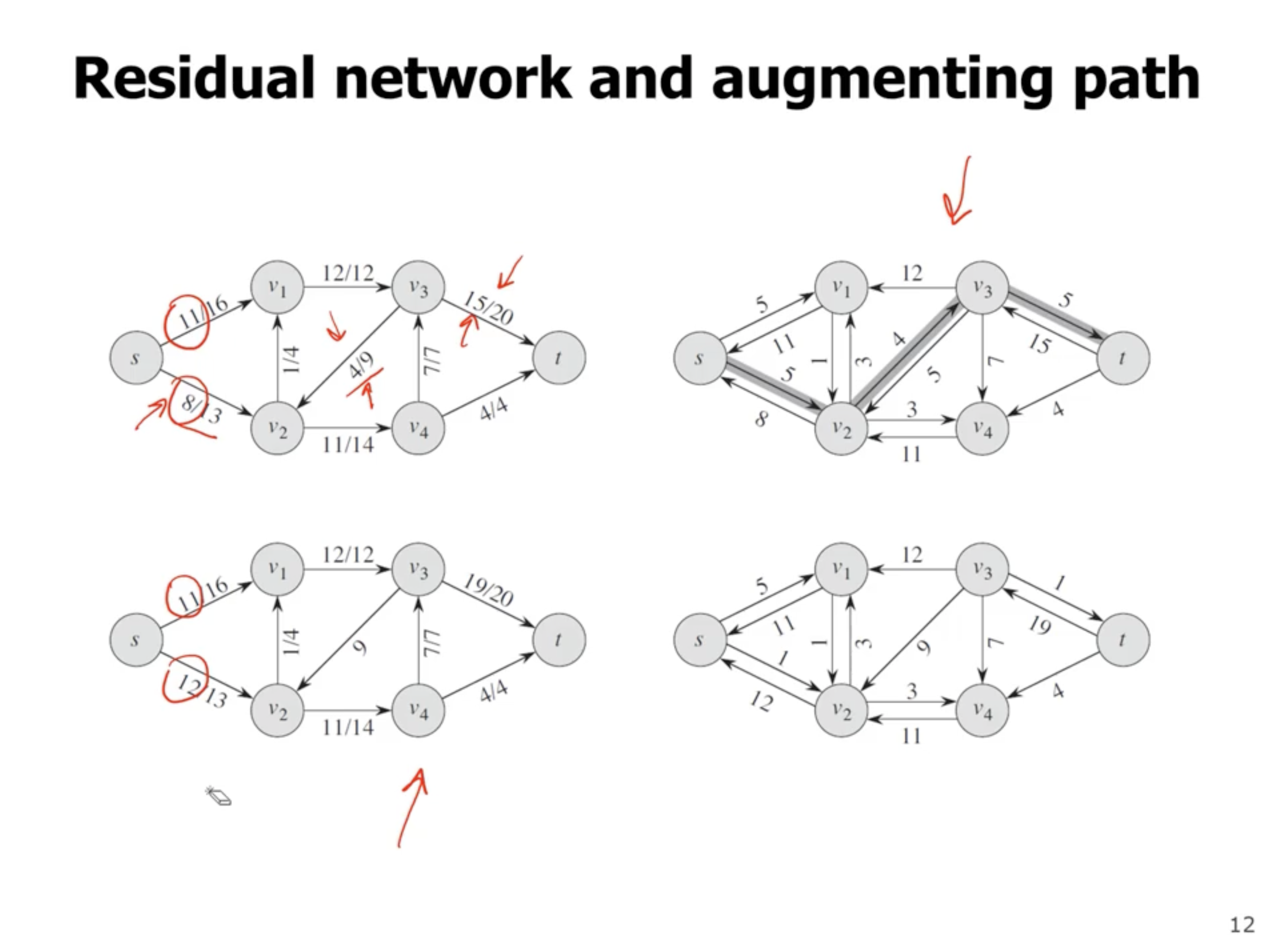
• there is no augmenting path left (can’t find path from source to sink), so the max flow of the previous graph is the answer

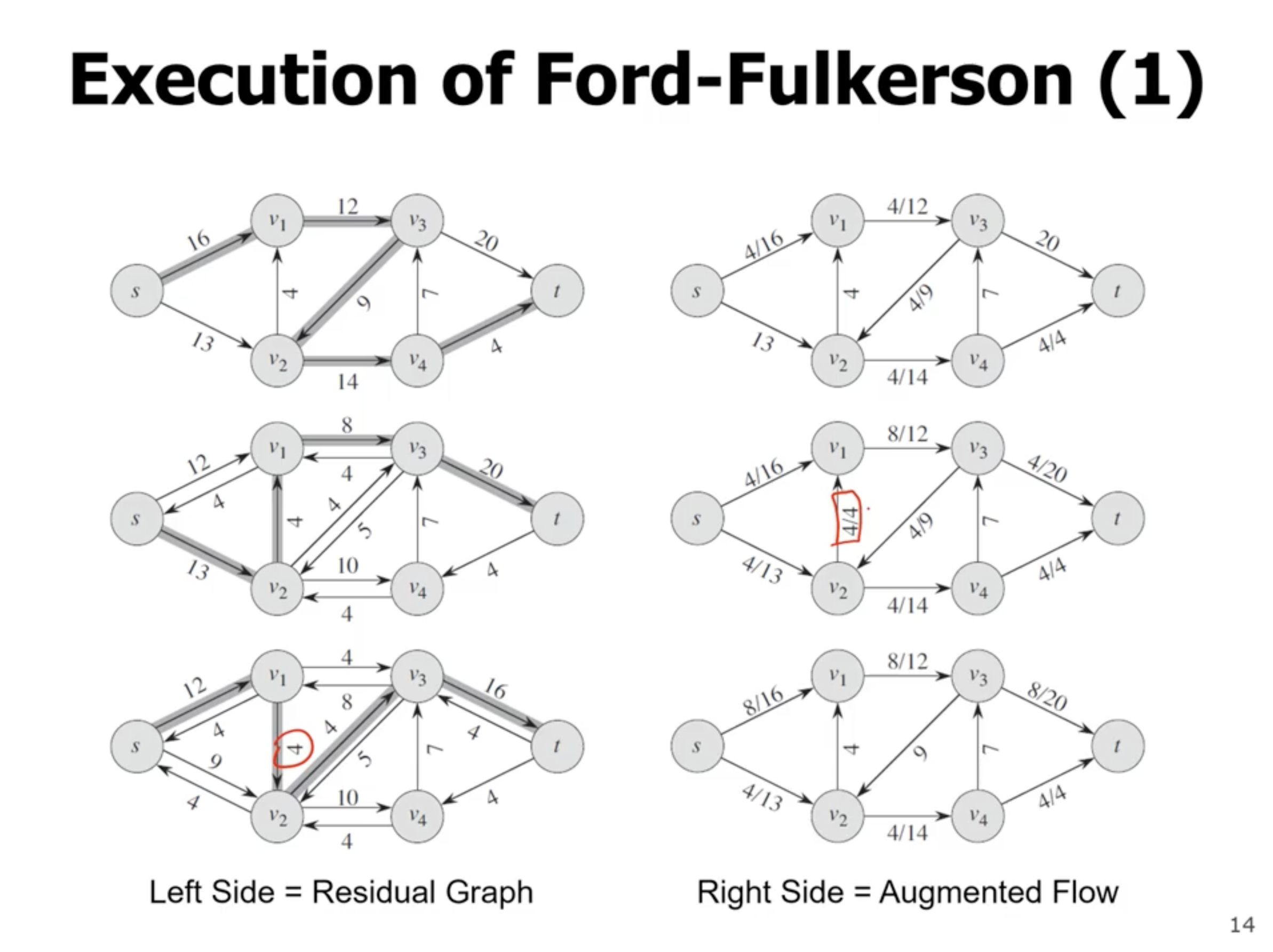
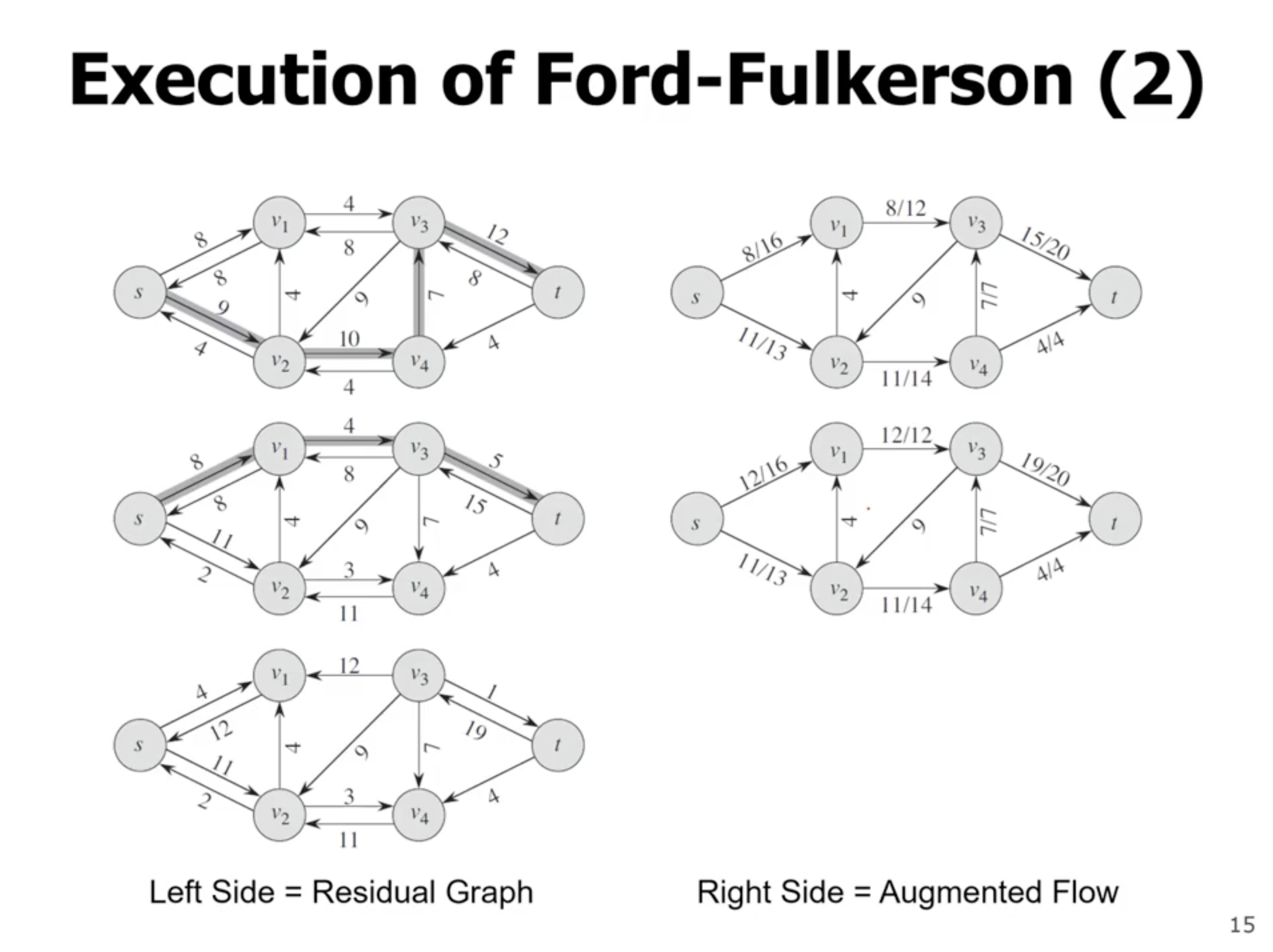
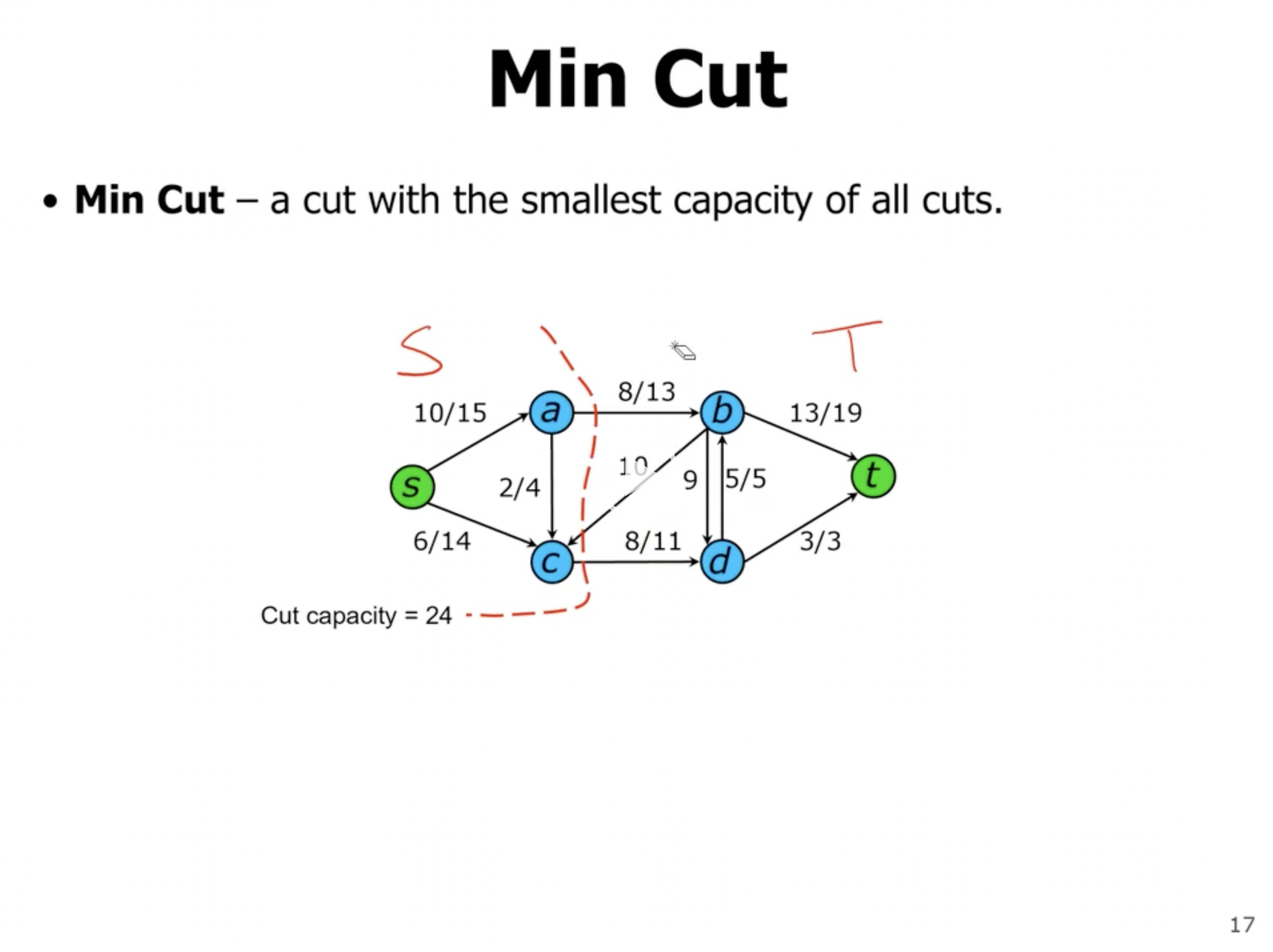
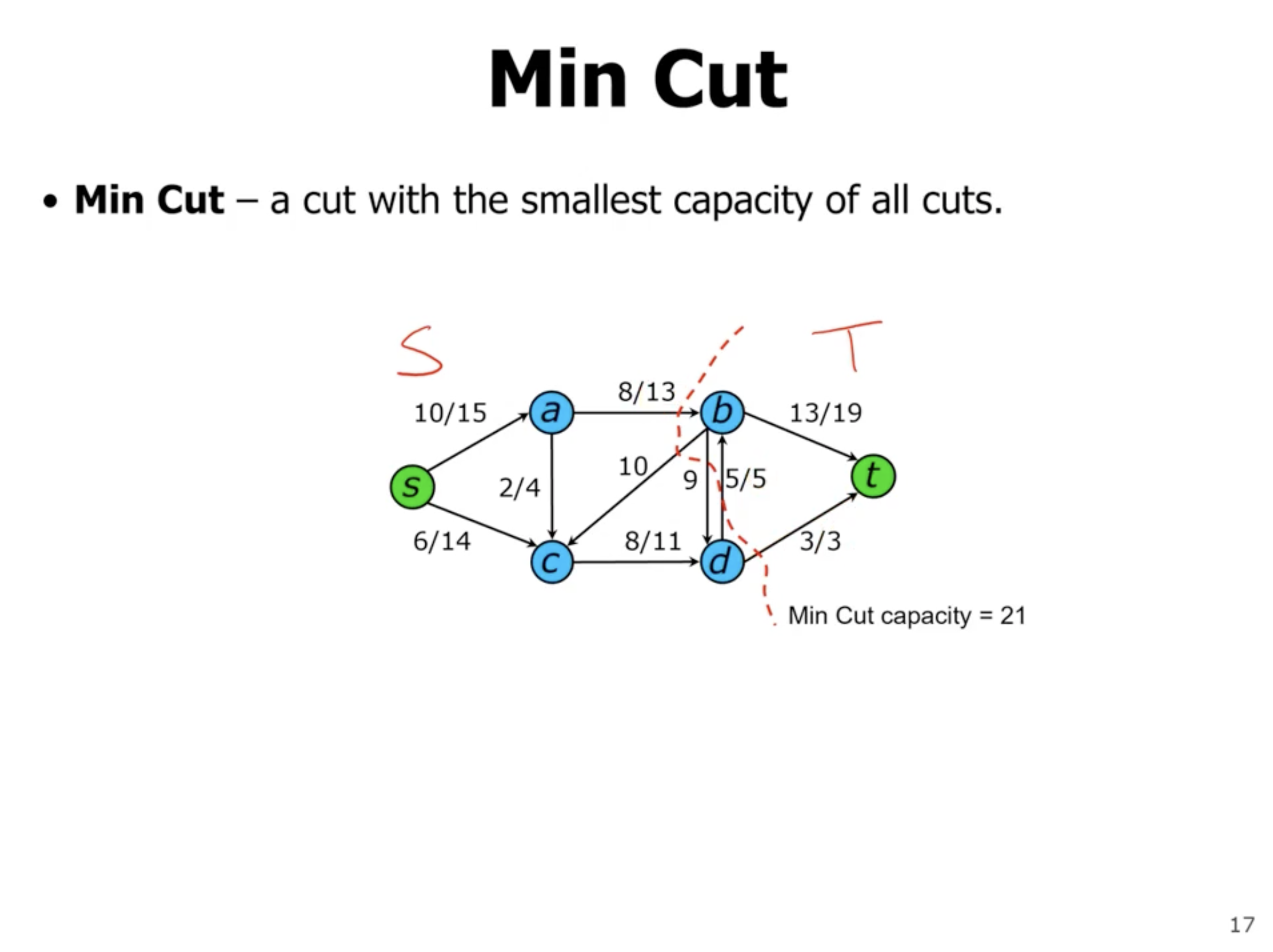
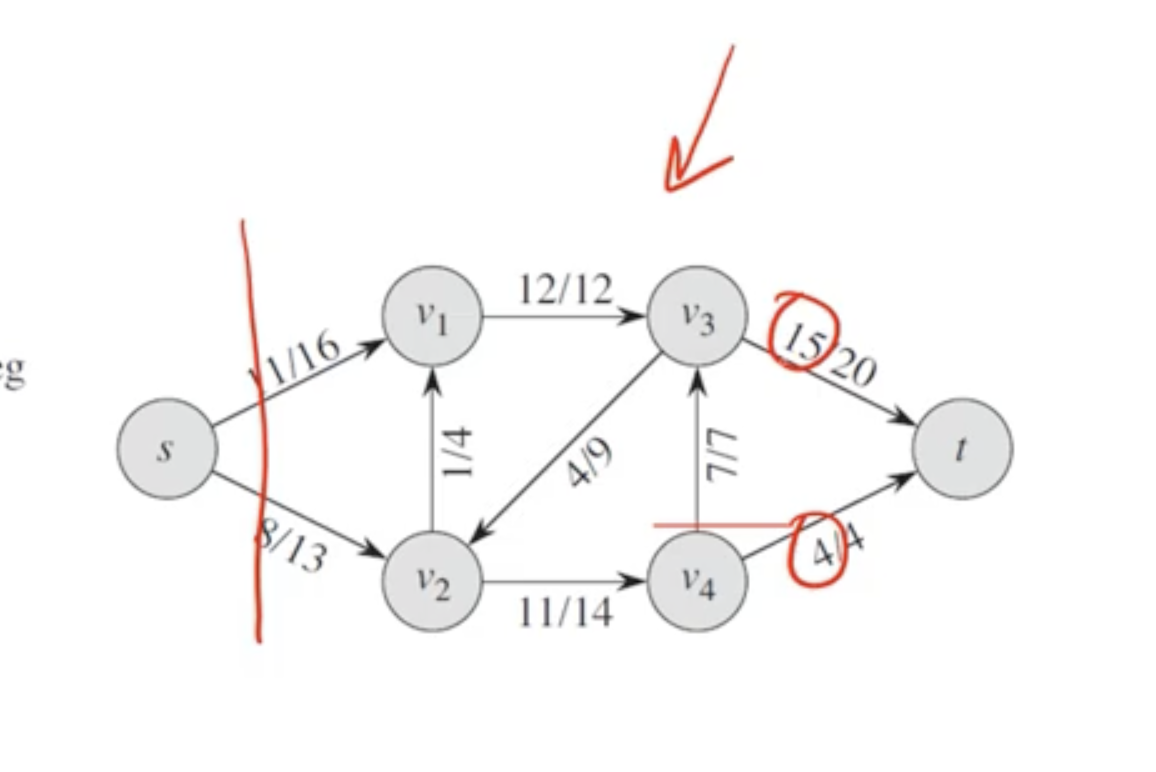
• the max flow of the network will be less than or equal to a cut

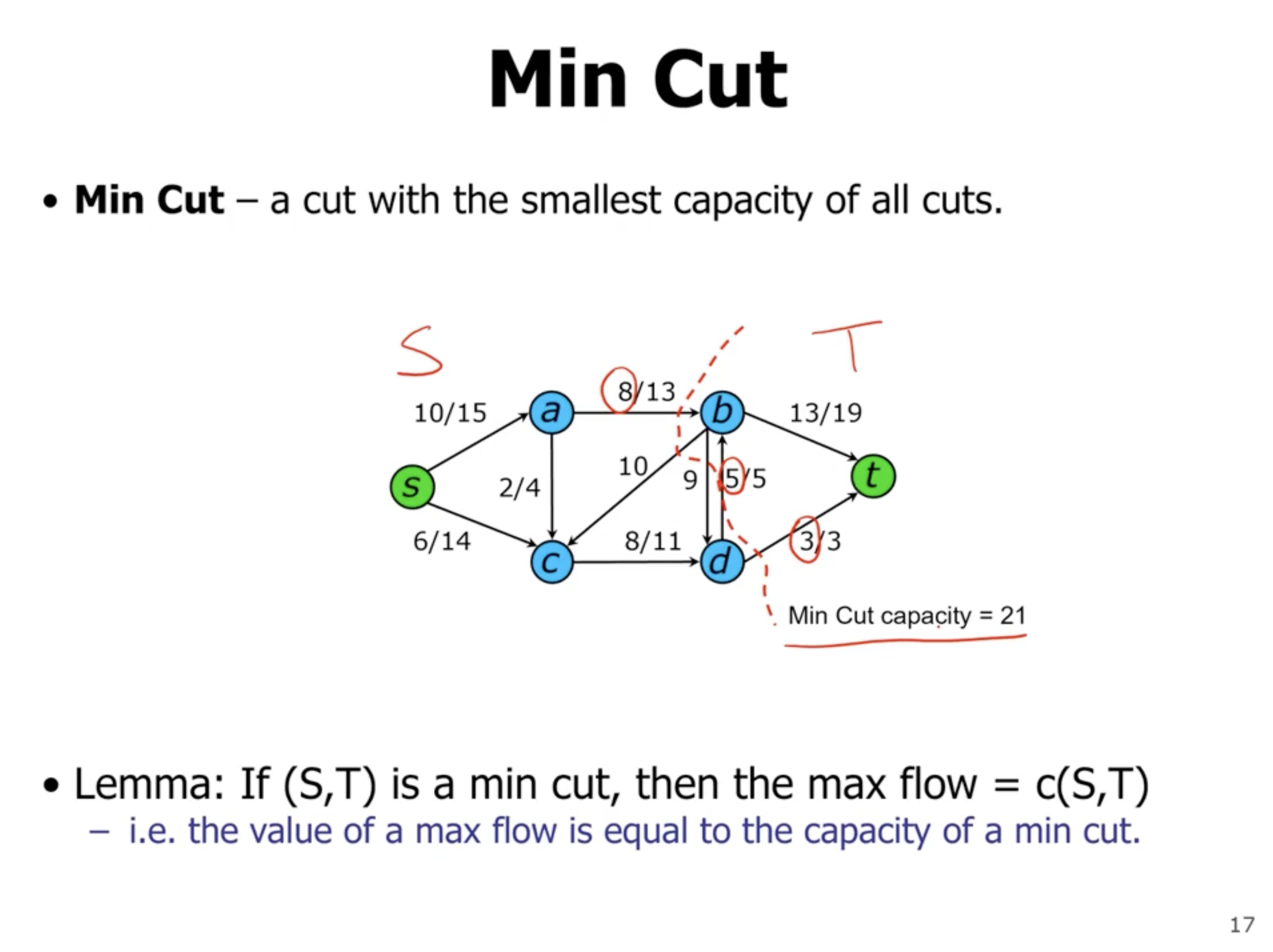
• the max flow is the min cut

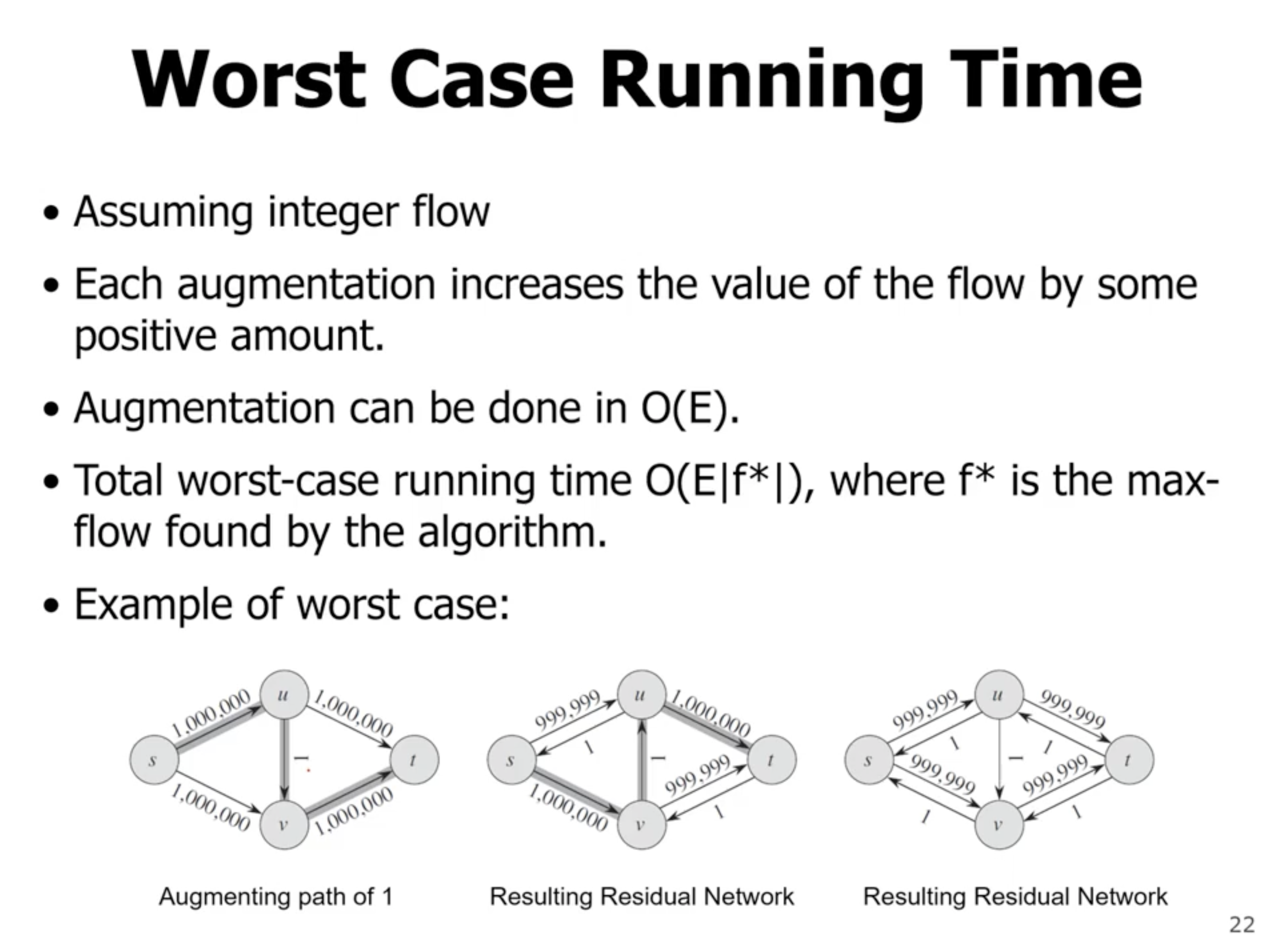
Edmonds-Karp algorithm #

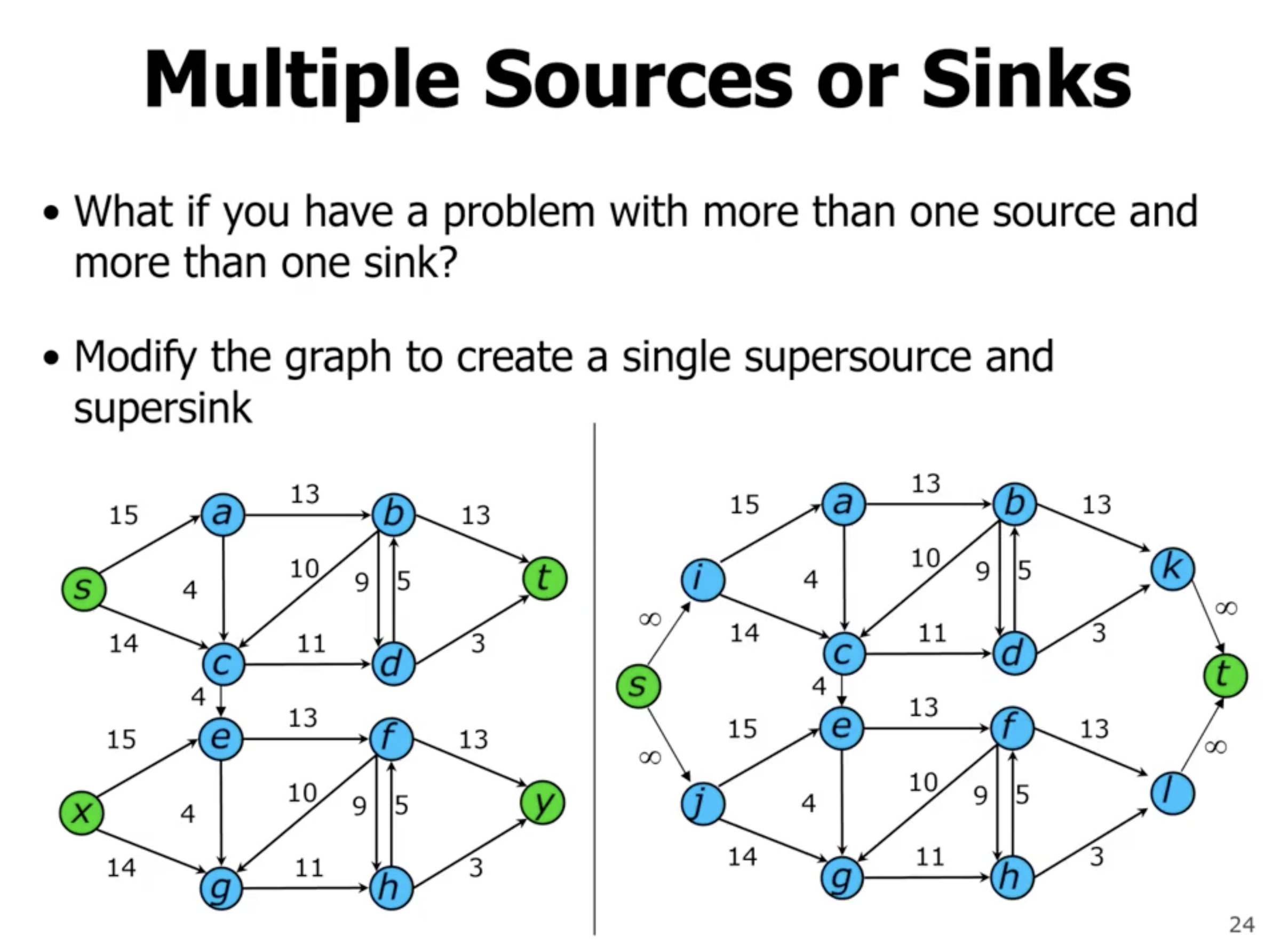
Multiple sources or sinks #

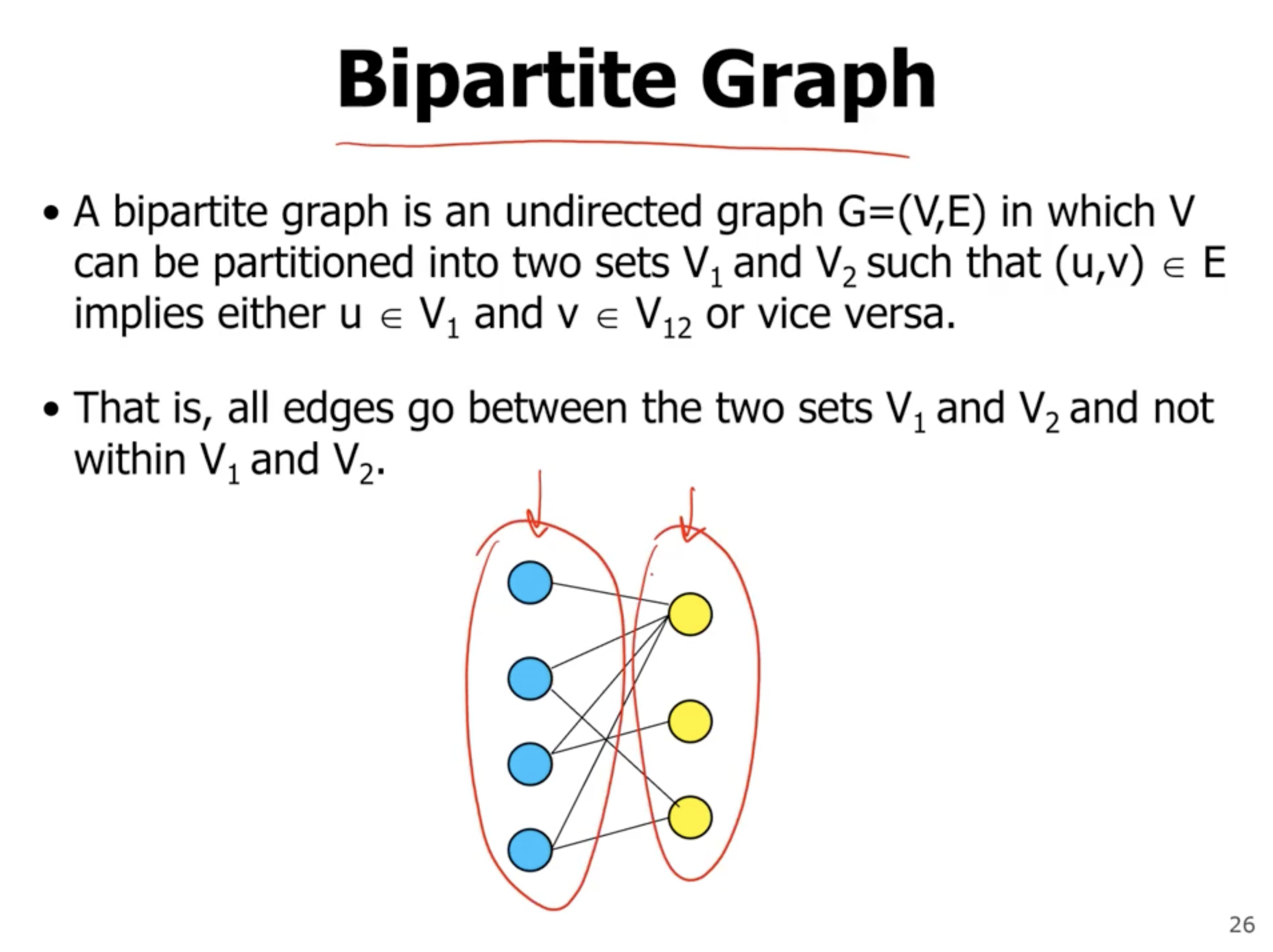
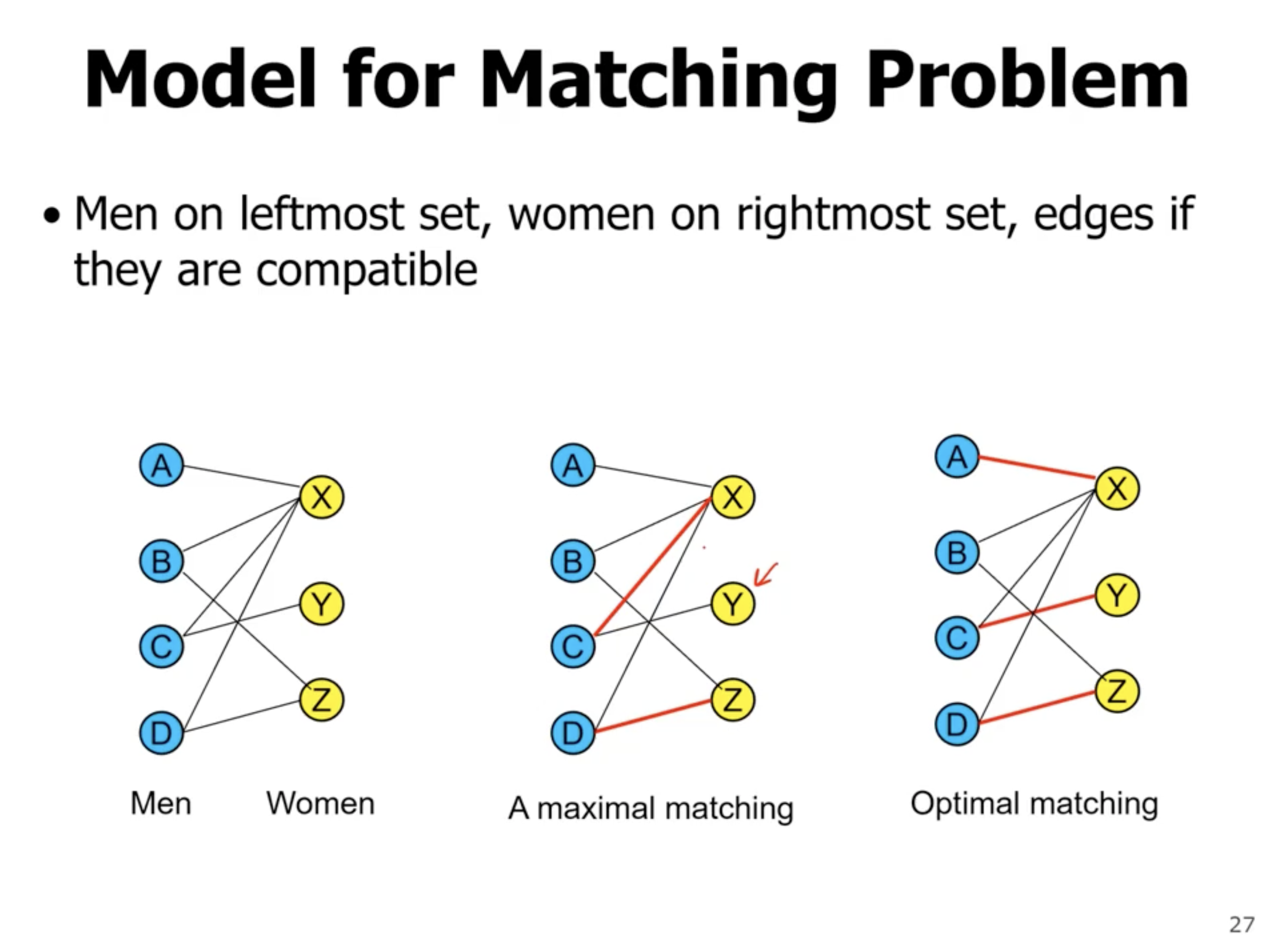
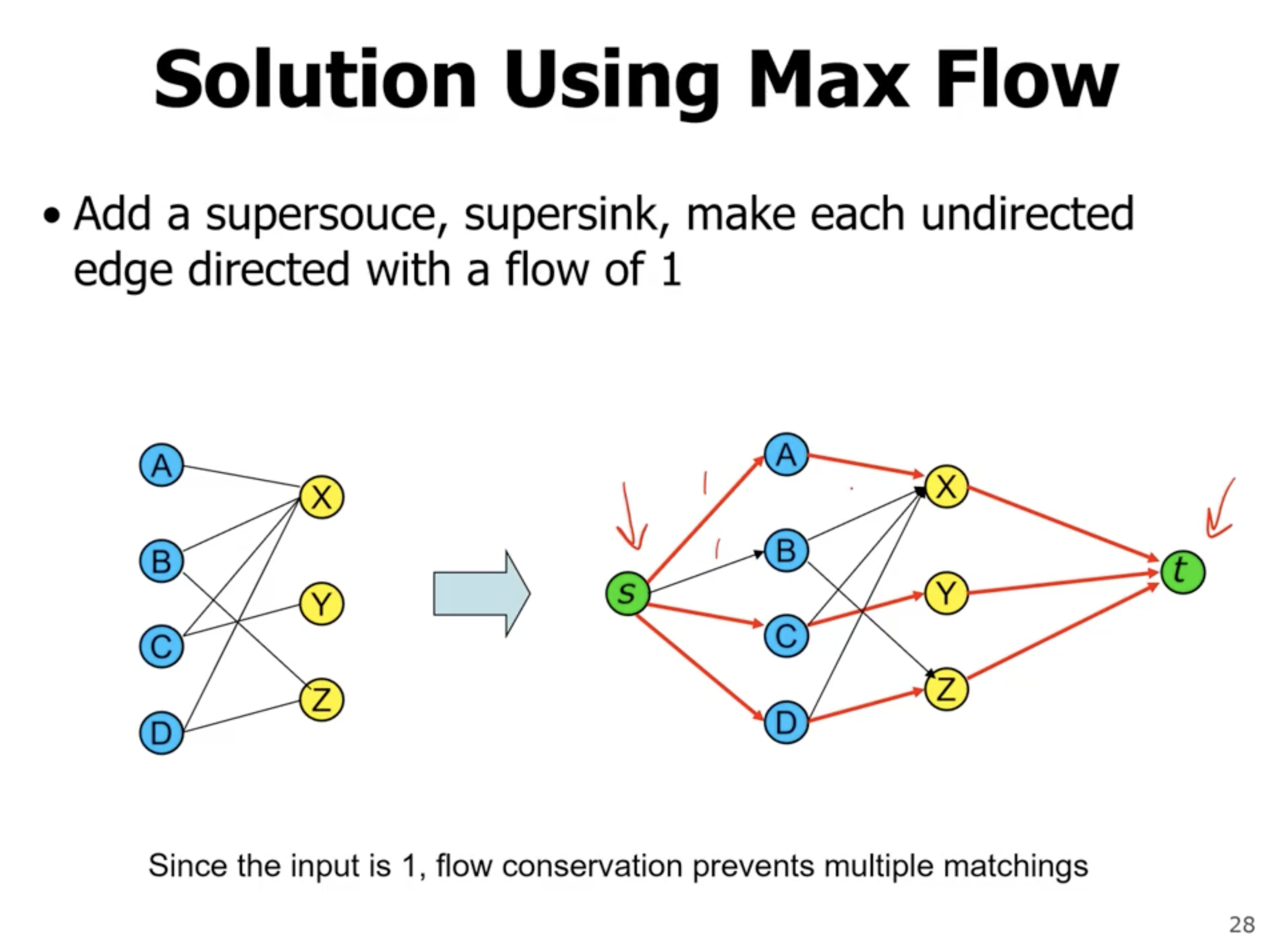
Bipartite matching #