Matrix-chain multiplication #
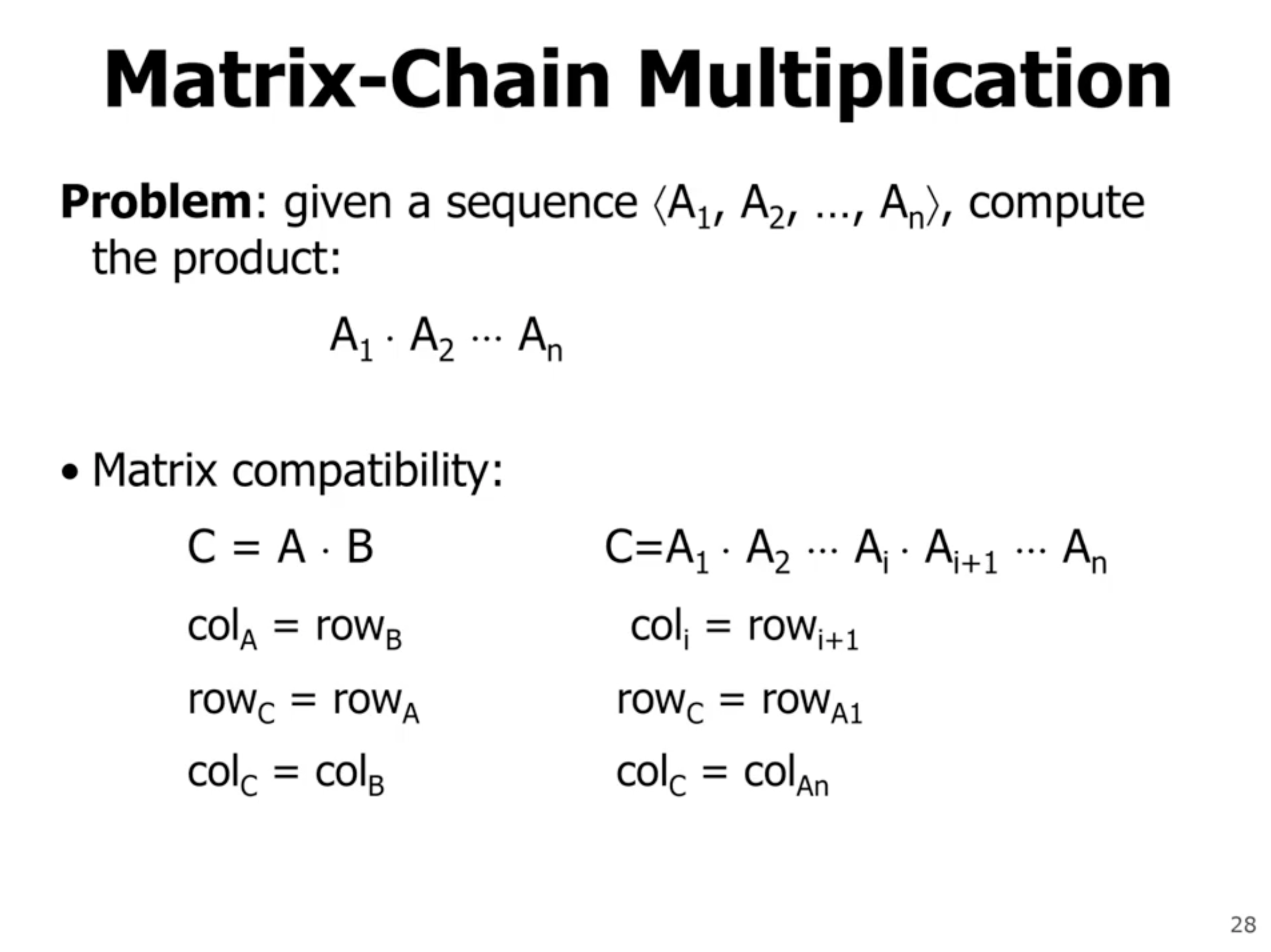

- total time complexity of \( \Theta(mnp) \)

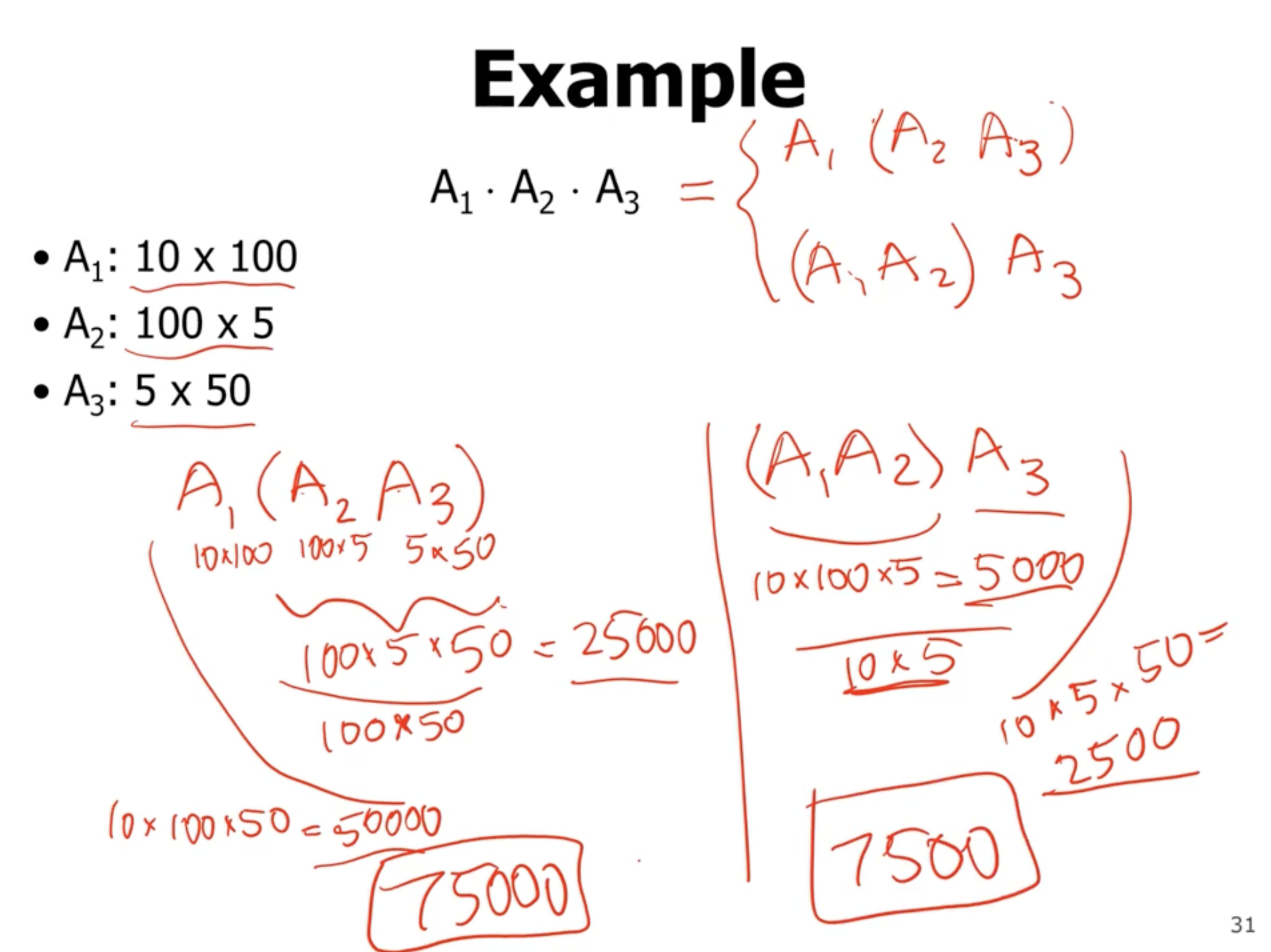



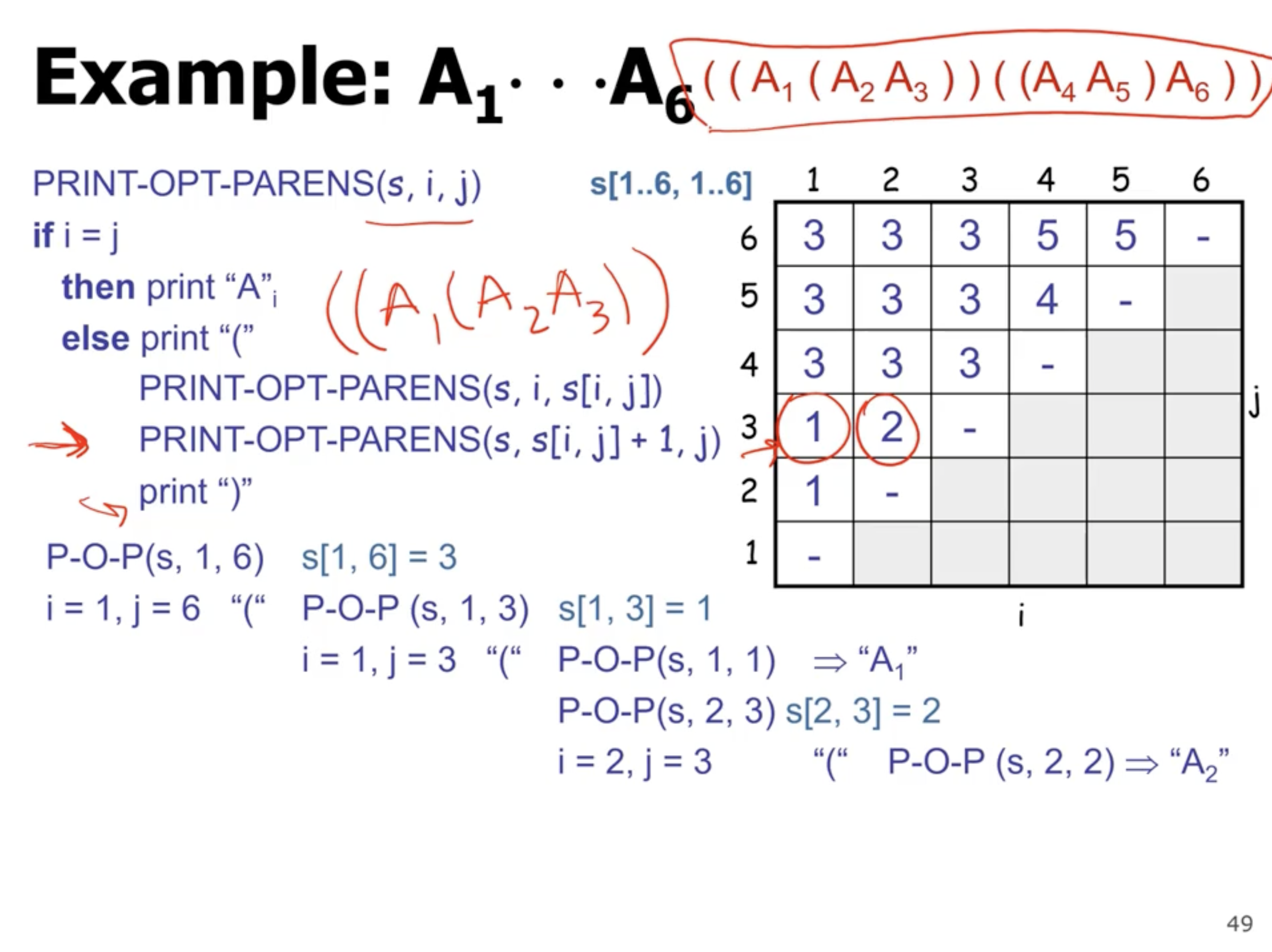
Optimal parenthesization #





- this results in exponential complexity
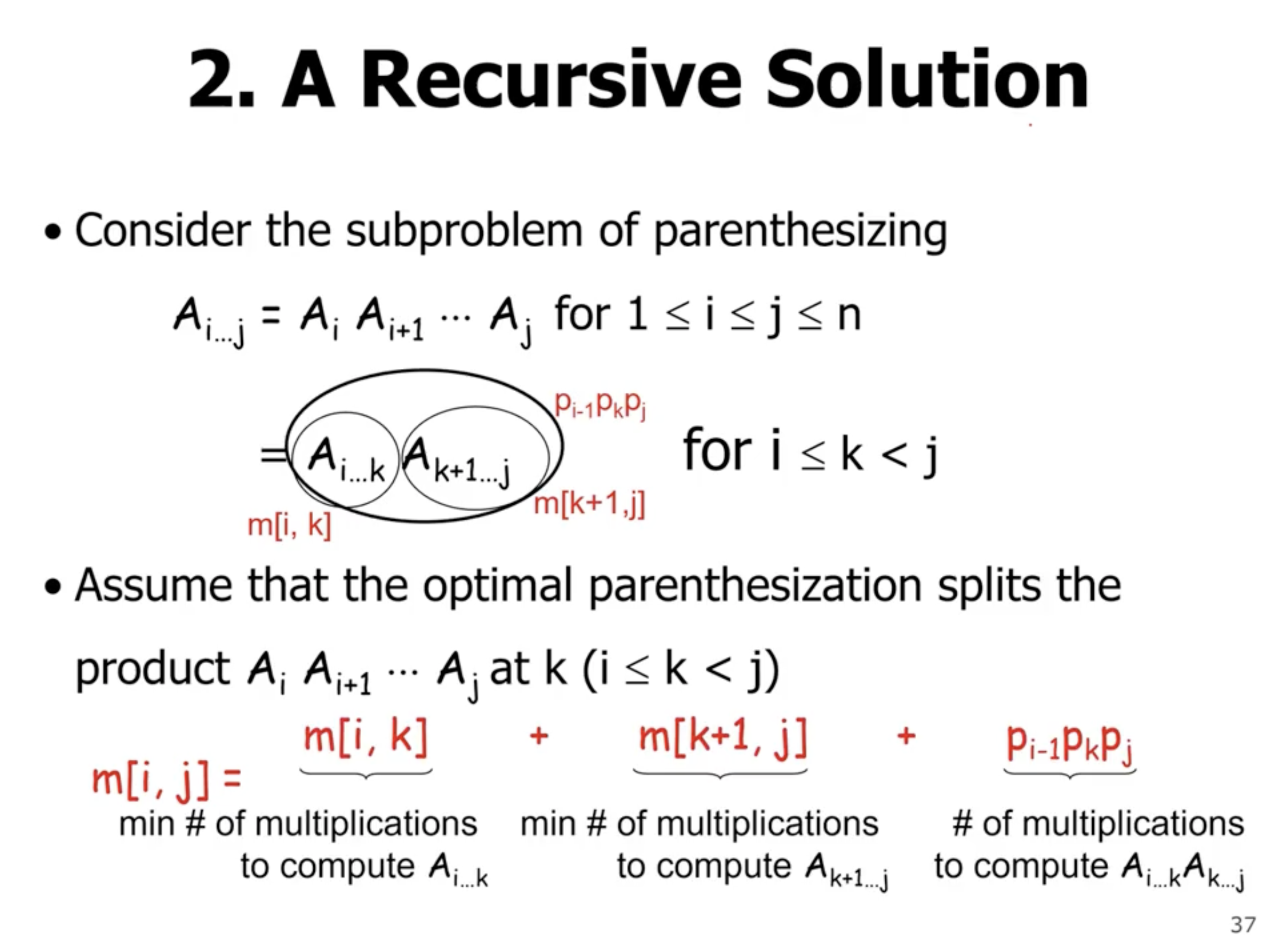
So let’s use dynamic programming:

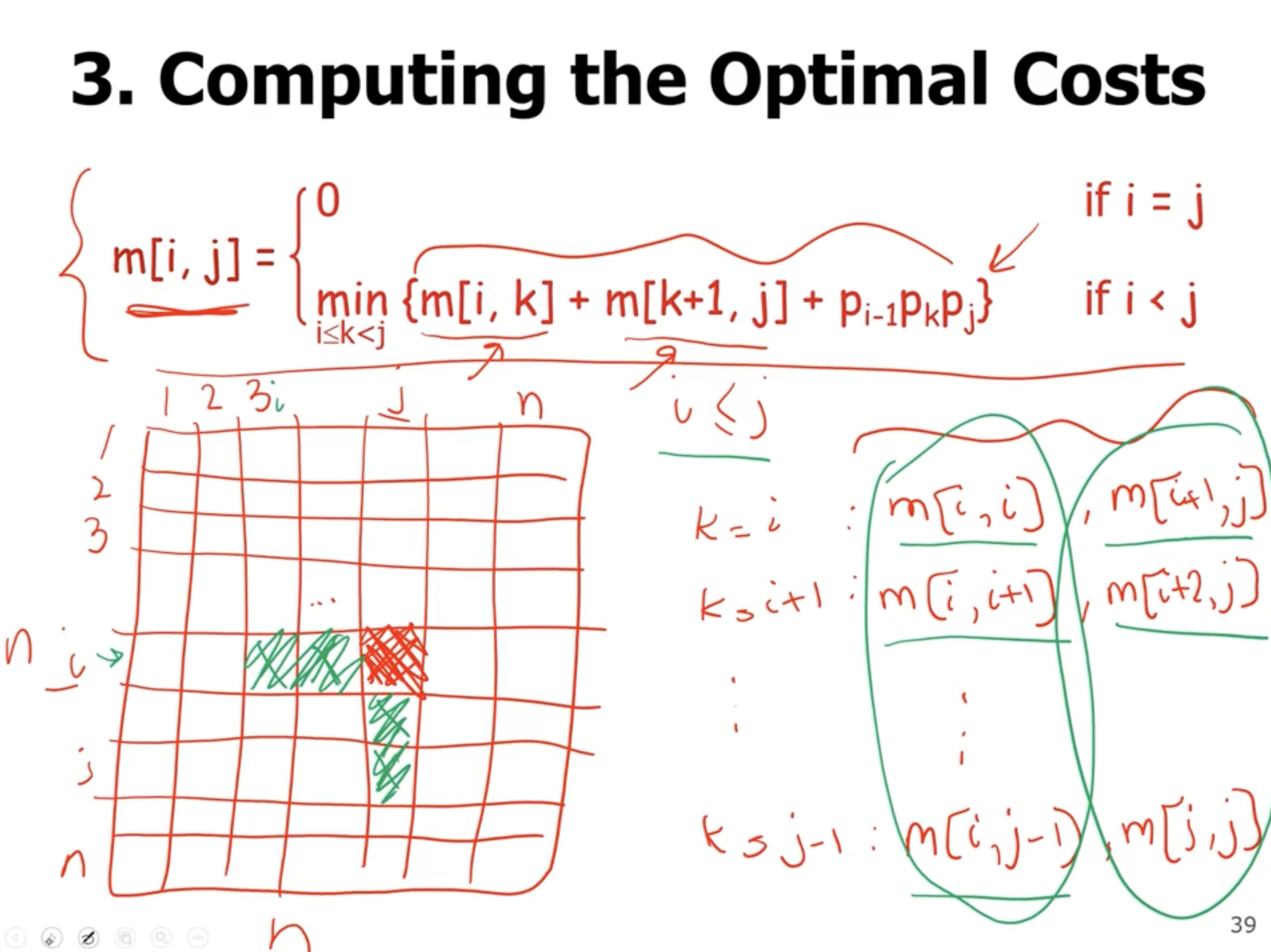
- make sure to start with the base case, when
i = j, the main diagonal of the array
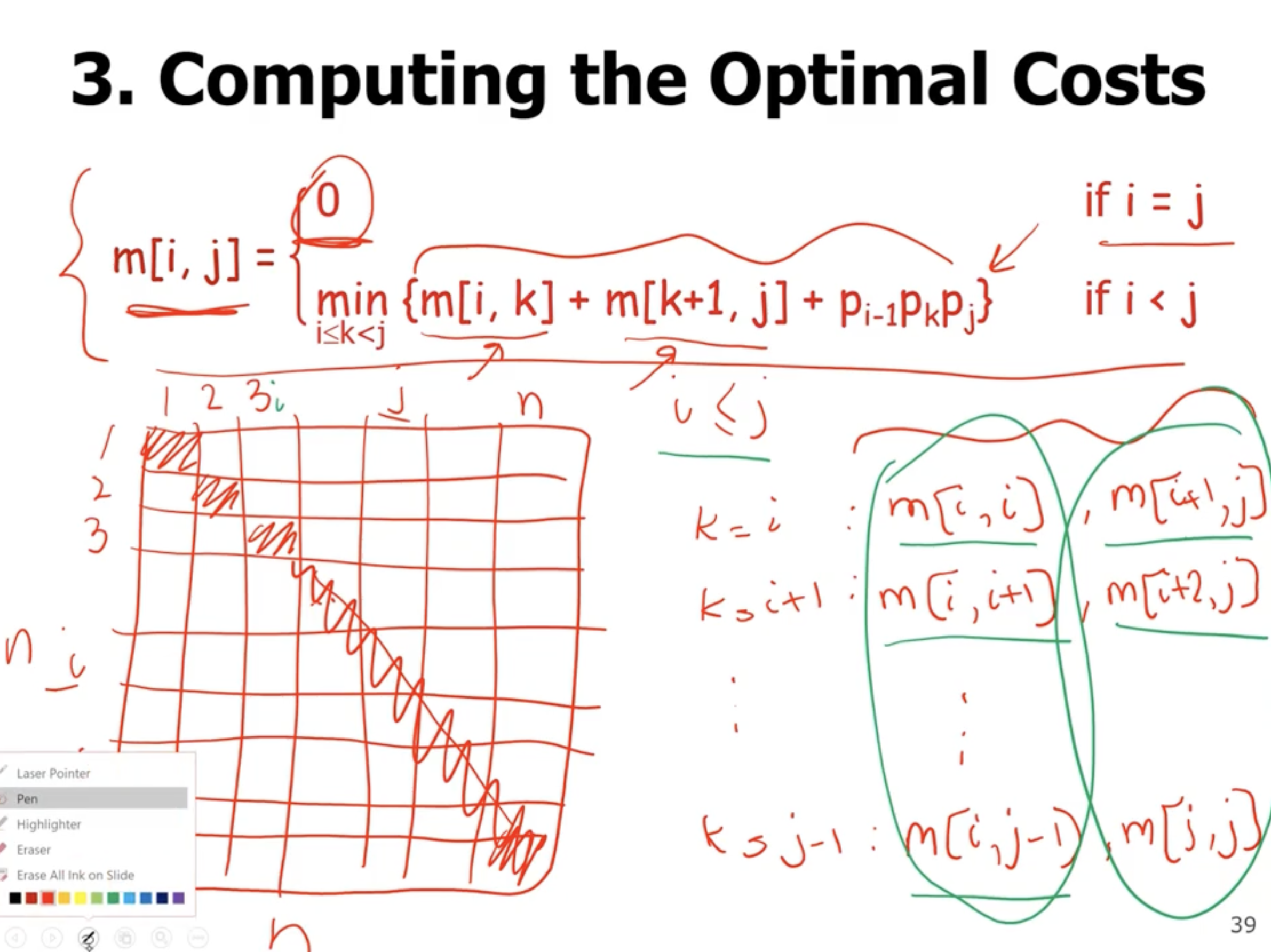
- then, we can start to fill in the spaces to the top right of each base case.
- note that the bottom left diagonal of the array will not be used, because
i > j
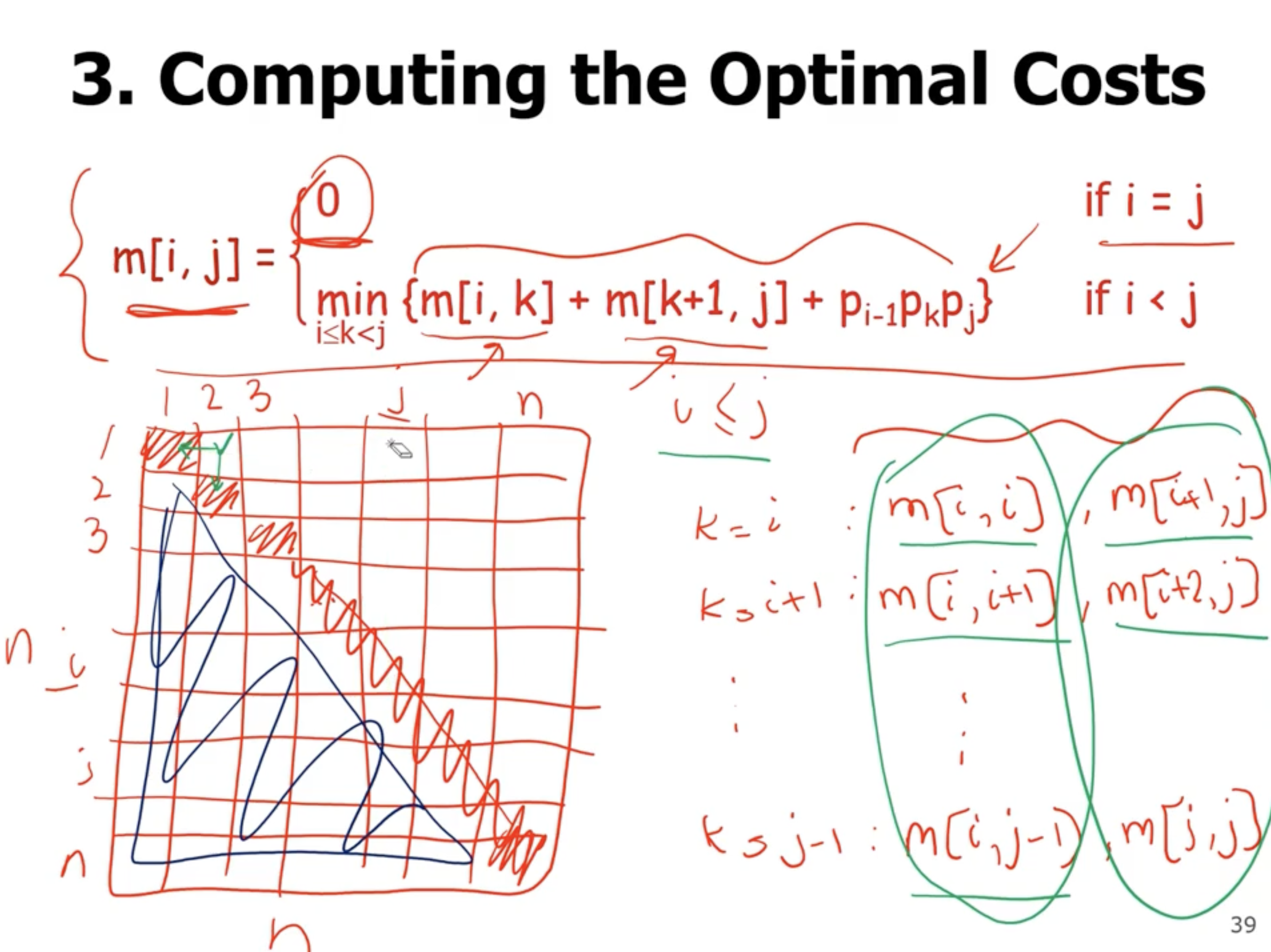


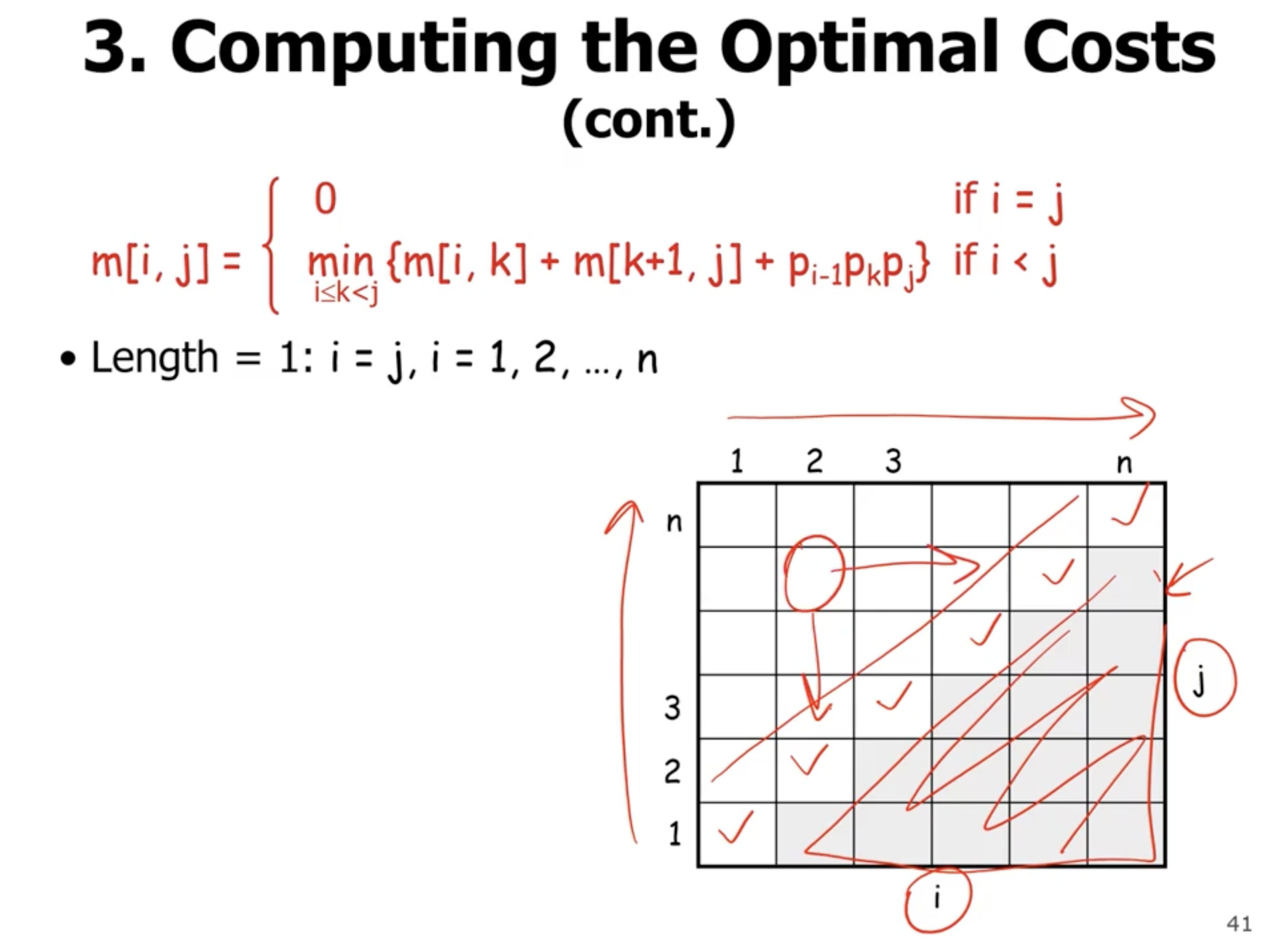
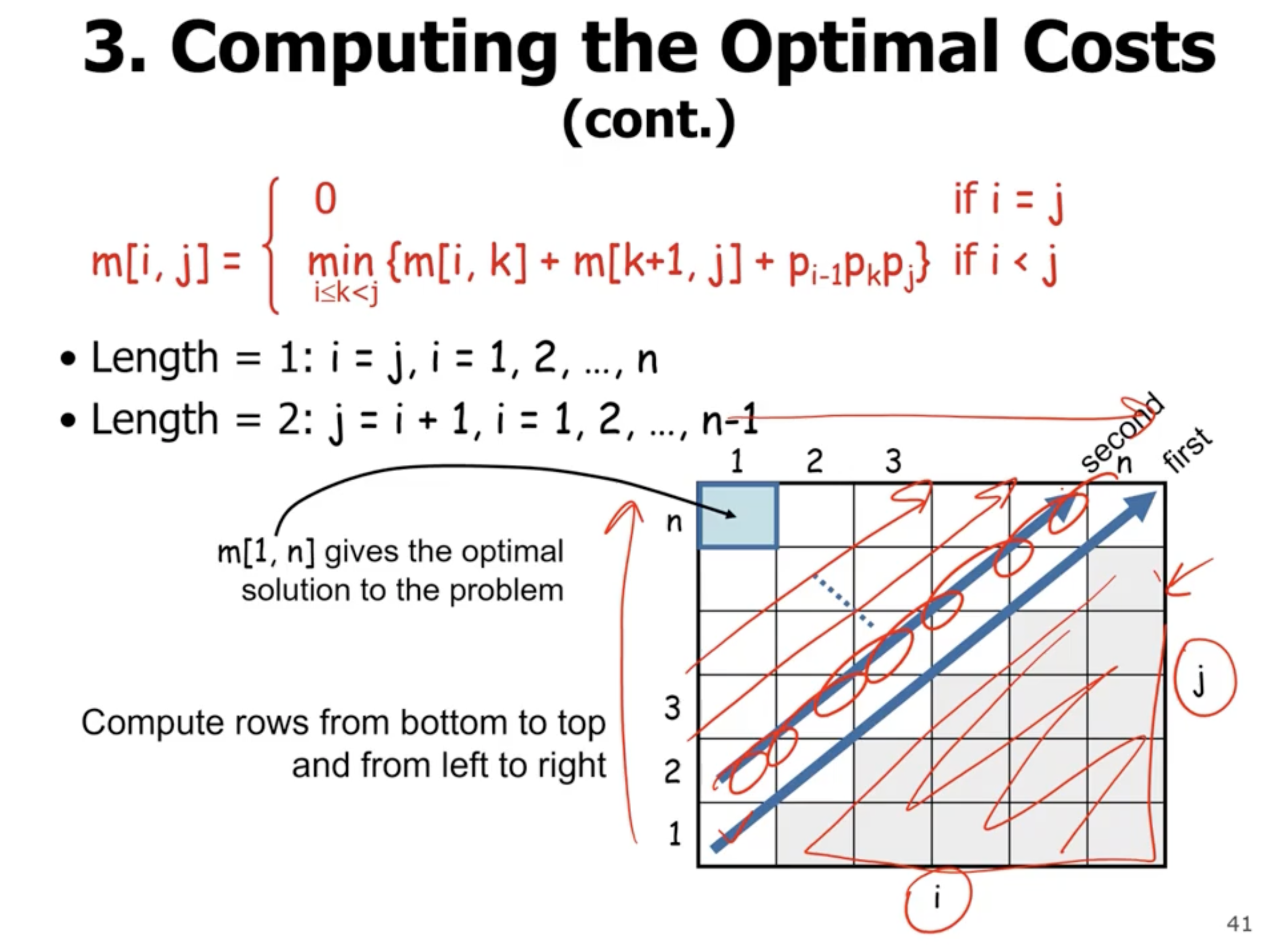
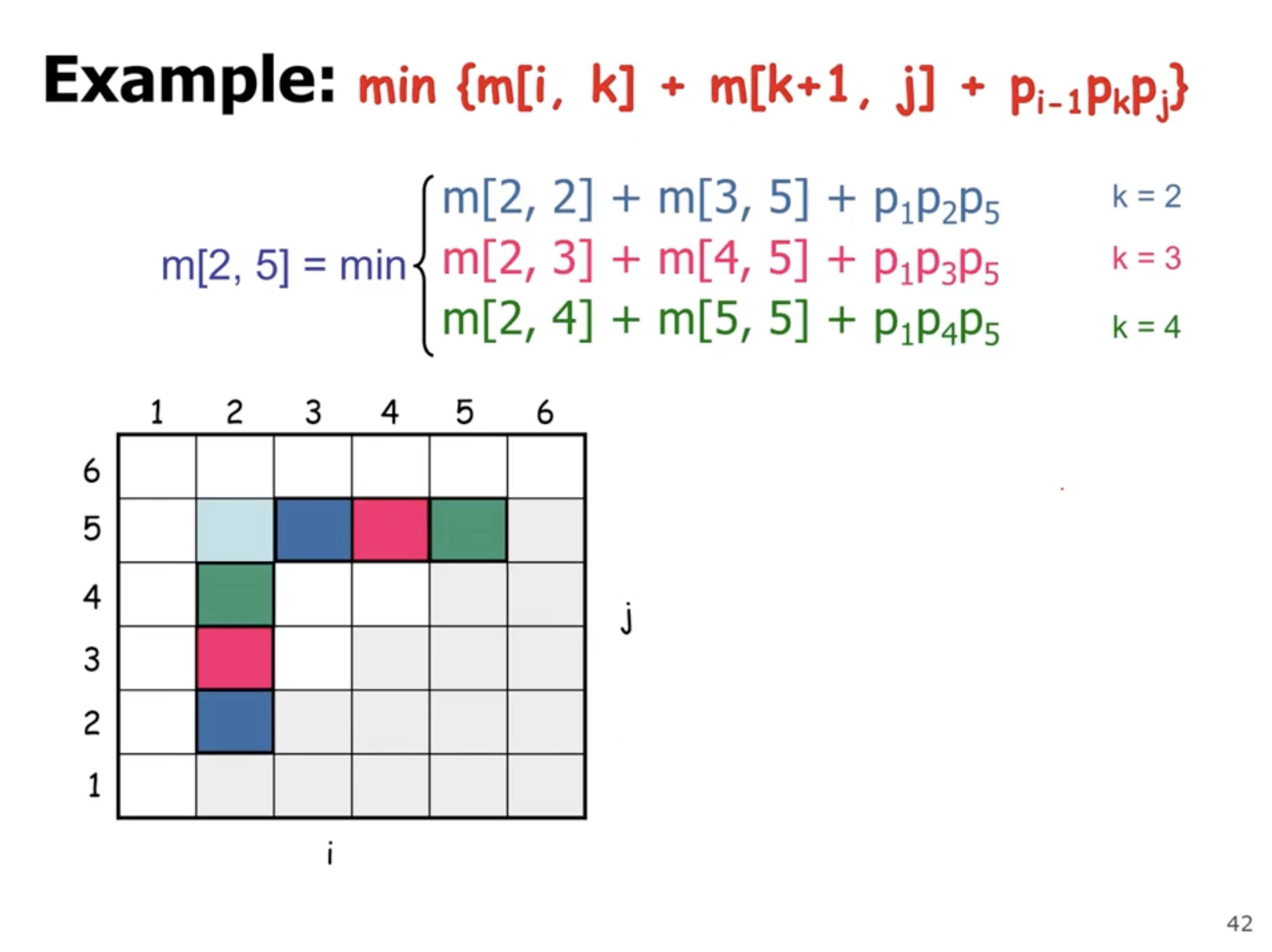


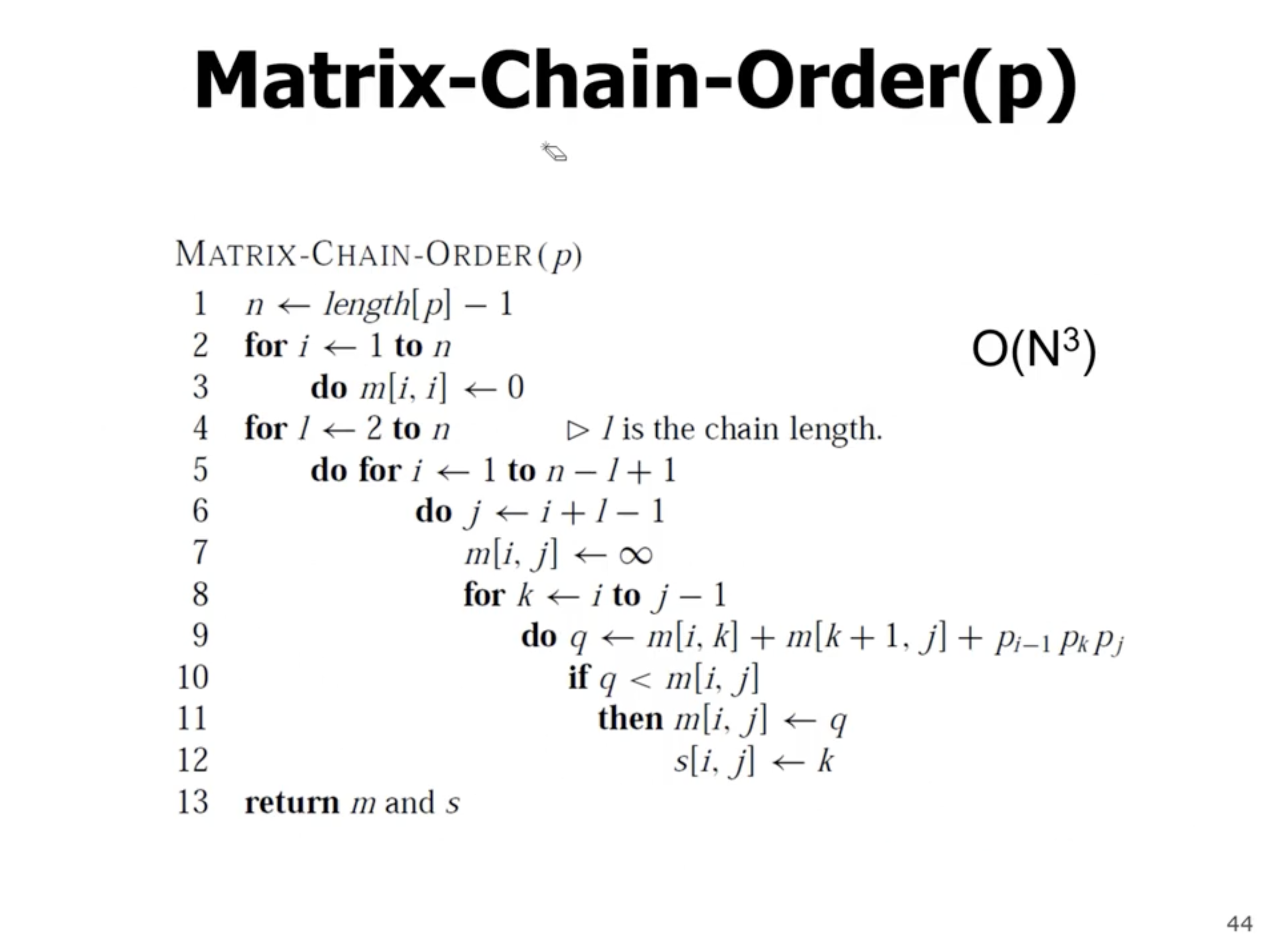
- start with the base cases
- loop over rows and columns
- solve sub problems in each level
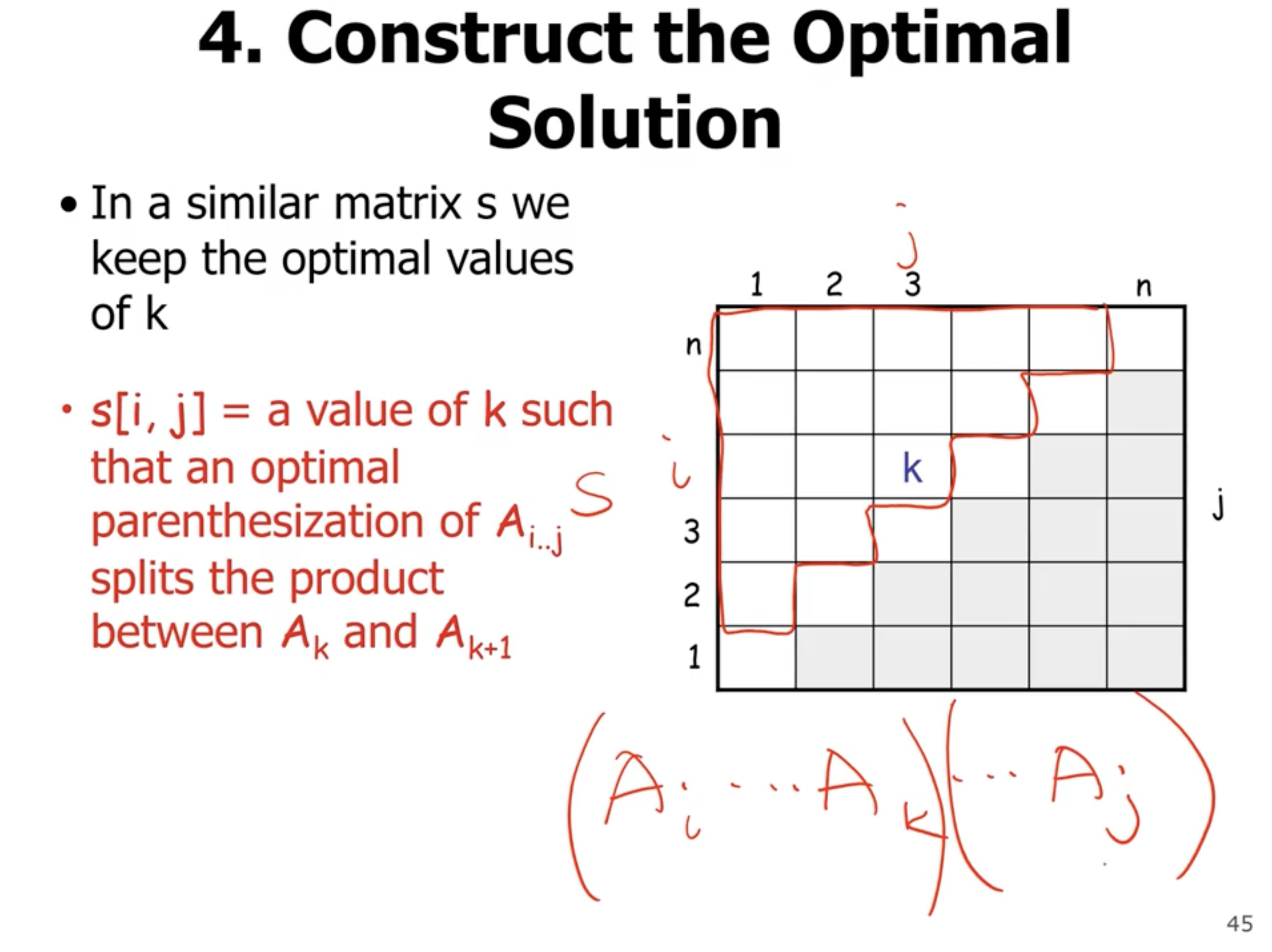
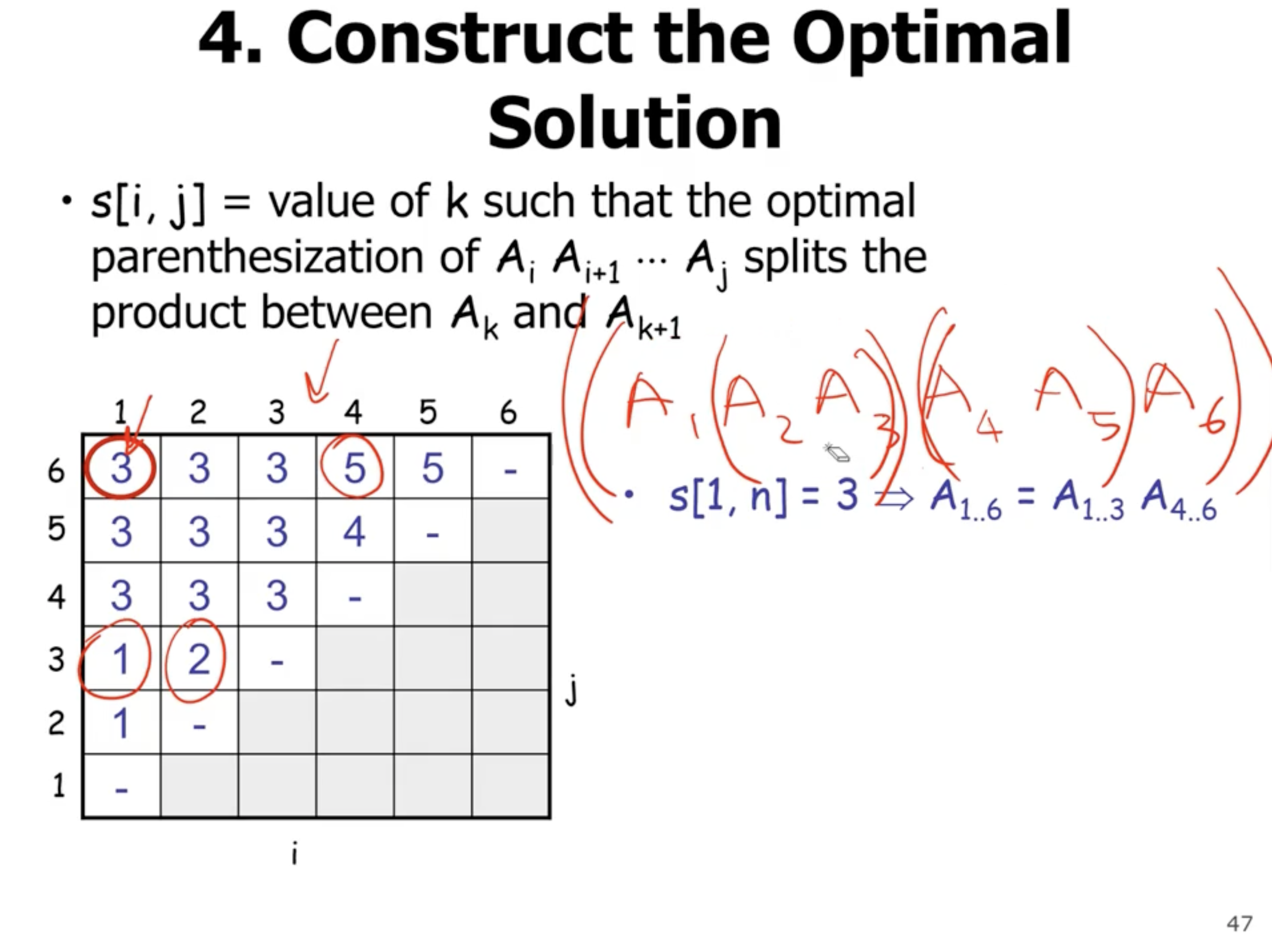
So how do we find the optimal solution once we’ve filled in the entire matrix? We can store the \( k \) value that gives the min value (this is the last line of the pseudo above).


My solution in Python
Output
0 50000 7500
-1 0 5000
-1 -1 0
-1 0 0
-1 -1 1
-1 -1 -1
( A0 ( A1 A2 ))
7500 multiplications needed
0 6000 25000 90000 86000 86000 99200
-1 0 10000 60000 80000 82400 87200
-1 -1 0 100000 120000 96000 105600
-1 -1 -1 0 100000 84000 108000
-1 -1 -1 -1 0 24000 72000
-1 -1 -1 -1 -1 0 9600
-1 -1 -1 -1 -1 -1 0
-1 0 0 0 0 0 0
-1 -1 1 2 3 4 5
-1 -1 -1 2 2 2 5
-1 -1 -1 -1 3 3 5
-1 -1 -1 -1 -1 4 5
-1 -1 -1 -1 -1 -1 5
-1 -1 -1 -1 -1 -1 -1
( A0 ((((( A1 A2 ) A3 ) A4 ) A5 ) A6 ))
99200 multiplications needed