Piplined protocols #

Go-back-n #

unacked = unacknowledged = no ACK response, not confirmed for success yet.

The number of bits needed for a \( k \) -bit sequence numbers is \( 2^k - 1 \) . The window size is \( N = 2^k \) .

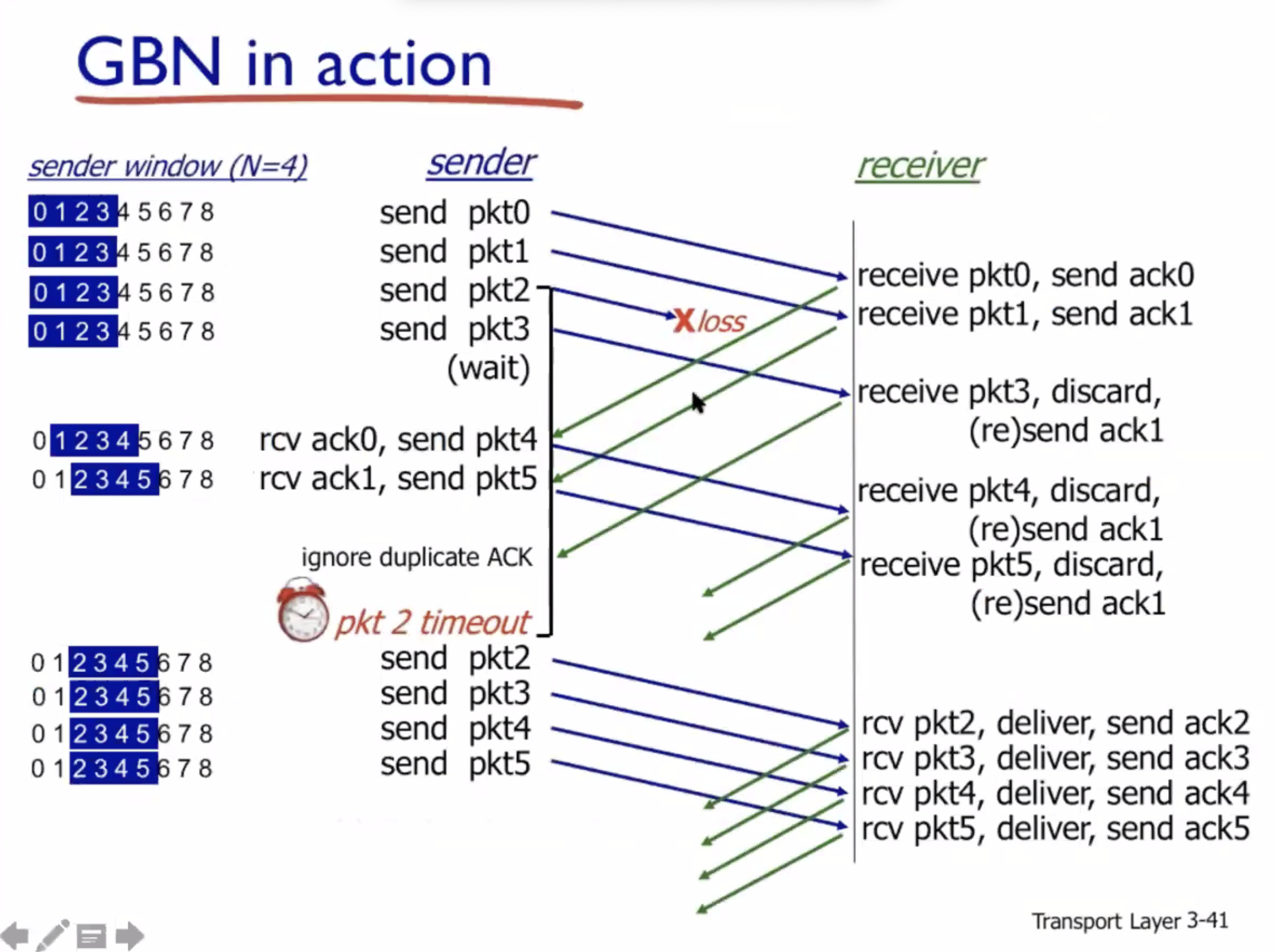
The packet number that can be used for cumulative ack should be the largest number before any gap.

https://media.pearsoncmg.com/aw/ecs_kurose_compnetwork_7/cw/content/interactiveanimations/go-back-n-protocol/index.html

1. Send window size \( N \) : it can send up to \( N \) packets on the fly
2. Cumulative ACK ( \( m \) ): means that packet \( m \) and also every packet before \( m \) are all received successfully
3. Timer: only a single timer, bound to the oldest packet unacked. When timeout, resend all packets in the sender window.
4. On receiver side, all packets after the gap are called “out of order”, and they are discarded. Hence, there can only be one gap.

Selective repeat #

For selective repeat, there is still \( k \) -bit sequence numbers, and a window size of \( N = 2^{k - 1} \) . The largest number is \( 2^{k - 1} - 1 \) .

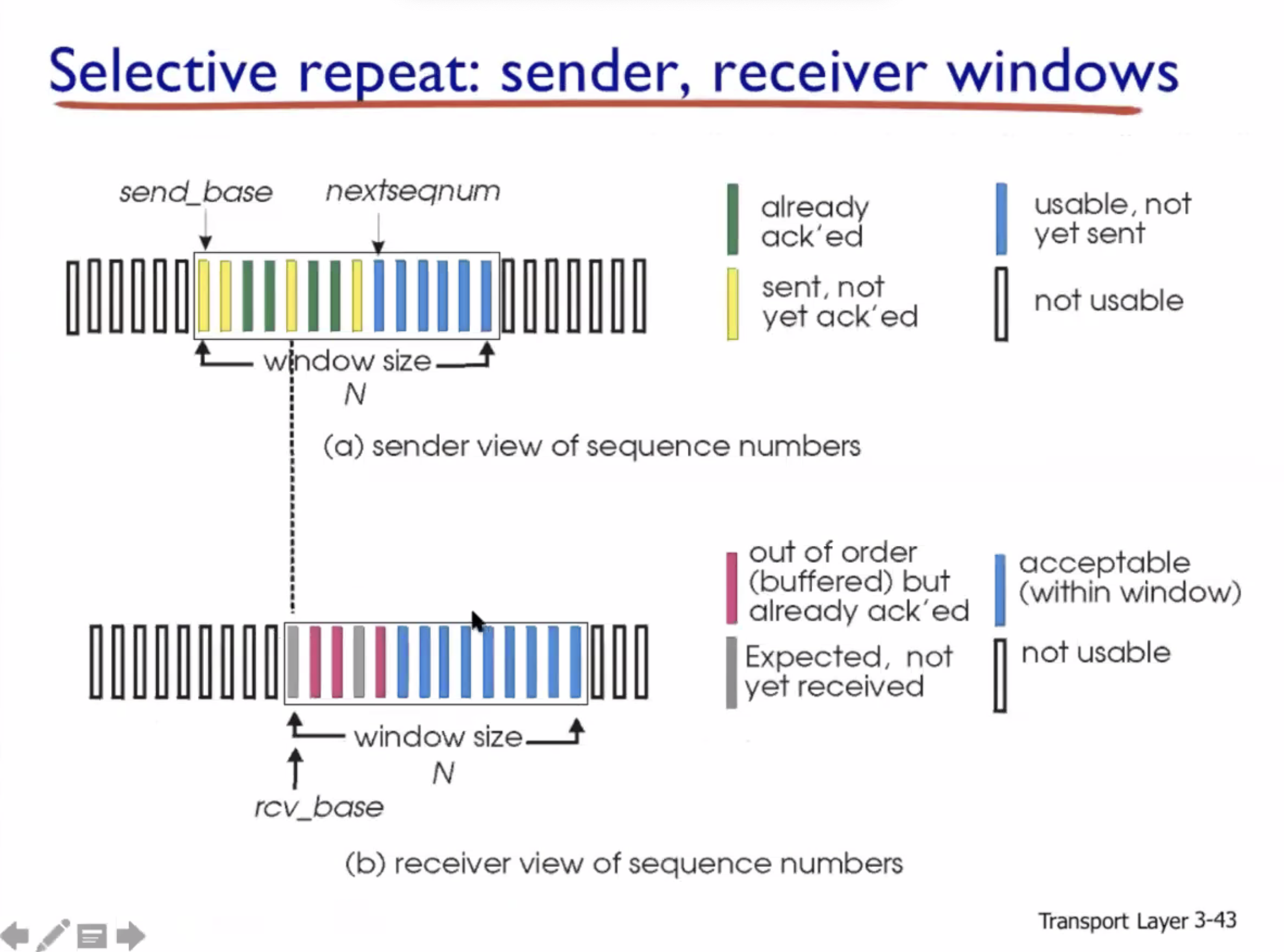
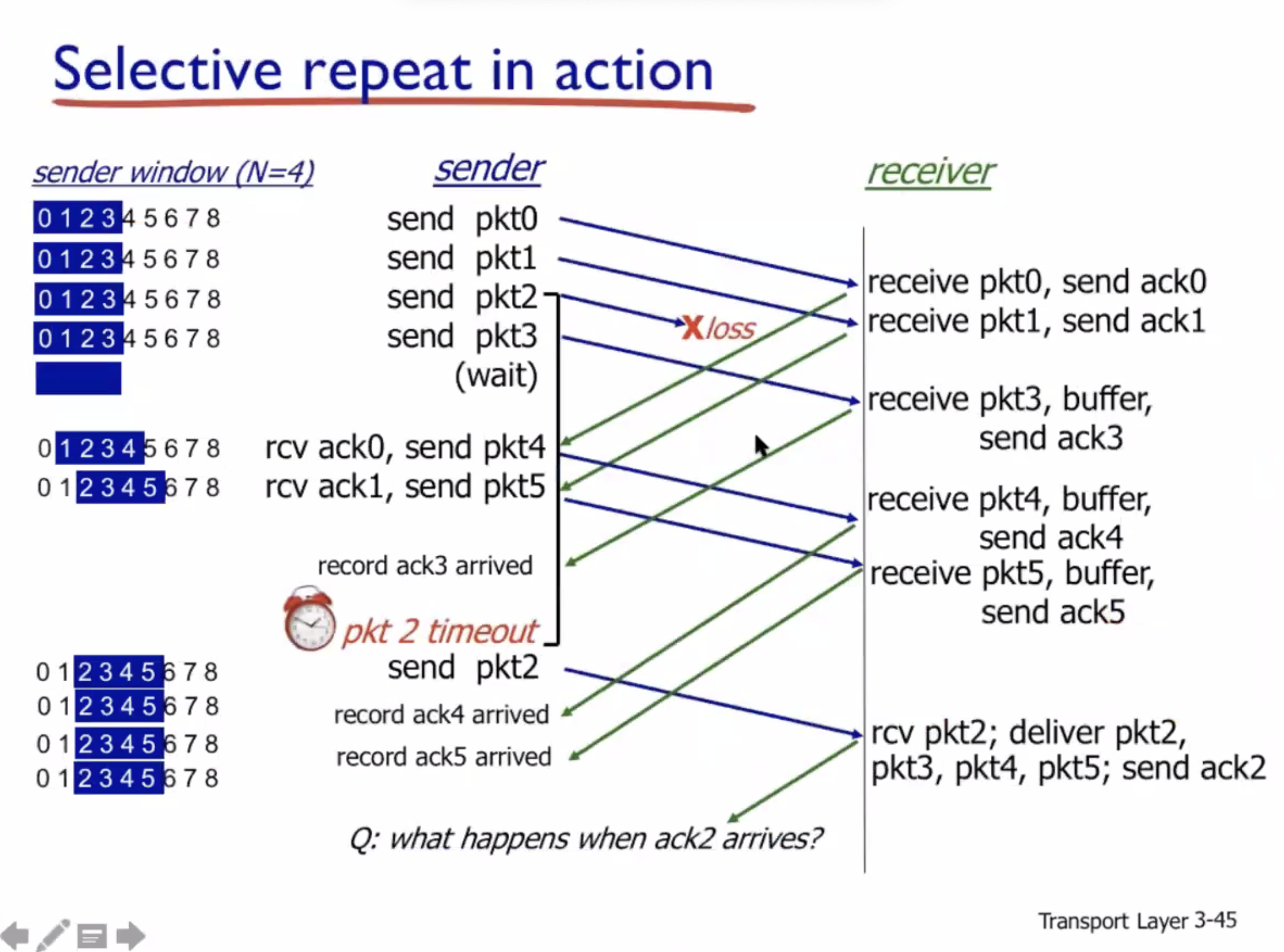
1. Send up to \( N \) packets: controlled by sender window size \( N \) .
2. Individual ACK: the particular packet received successfully.
3. Timer: there is one timer for each unacked packet. When timeout happens, the sender only resends the particular packet.
4. On receiver side: packets after gap are called “out of order”, but this time they are buffered, waiting to be delivered.

https://media.pearsoncmg.com/aw/ecs_kurose_compnetwork_7/cw/content/interactiveanimations/selective-repeat-protocol/index.html

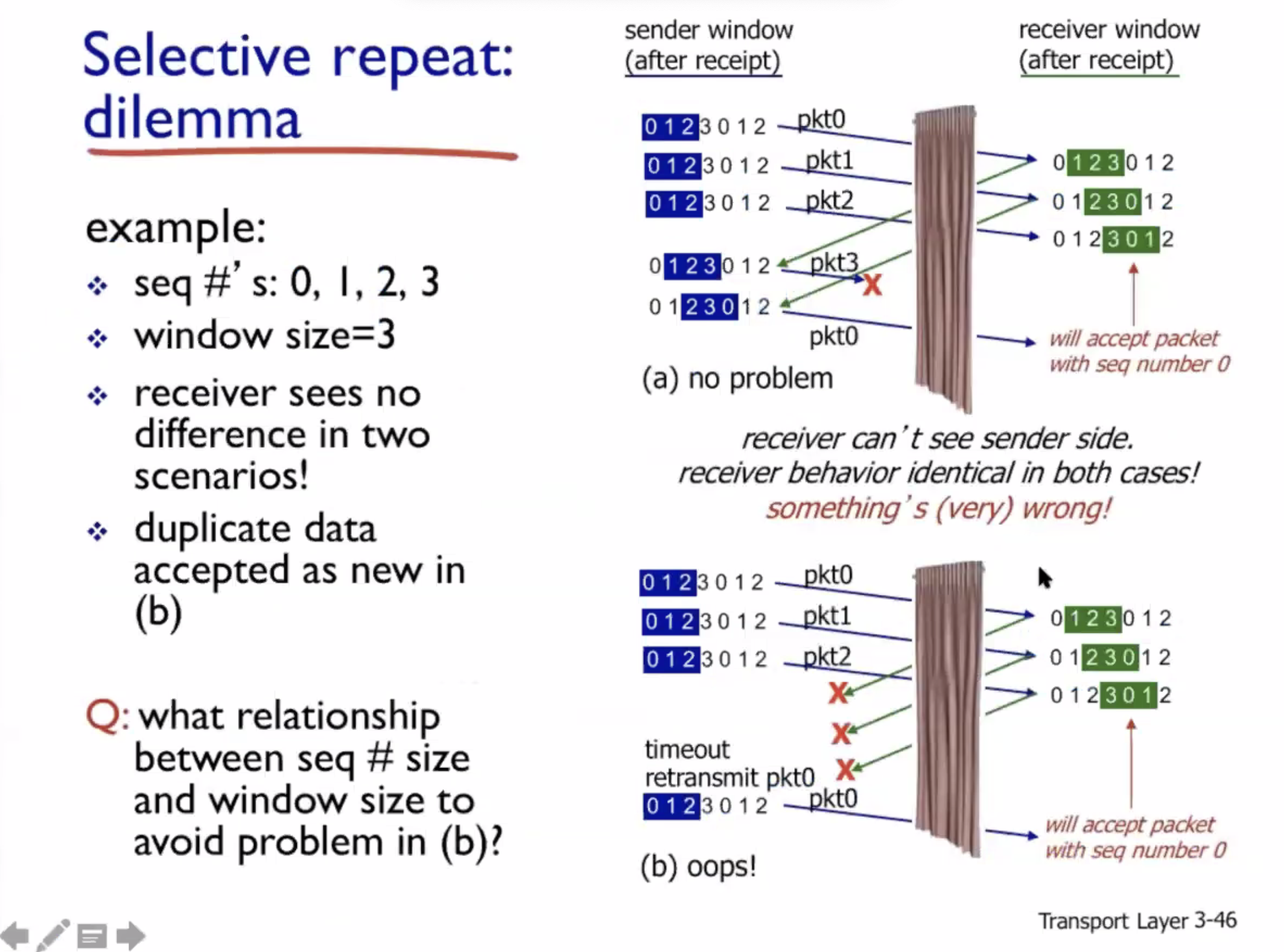
So to combat this, if \( k = 2 \) , then the size of the window should be \( N = 2^{2-1} = 2 \) . The largest sequence number is \( 2^{1 - 1} = 1 \) .