Finite state machine design cont. #
Moore machines #
- Output depends only upon present state
- If input changes, output does not change
- More number of states are required
- There is more hardware requirement
- They react slower to inputs (one clock cycle later)
- Synchronous output and state generation
- Output is placed on states
- Easy to design

Step 1: create a FSD
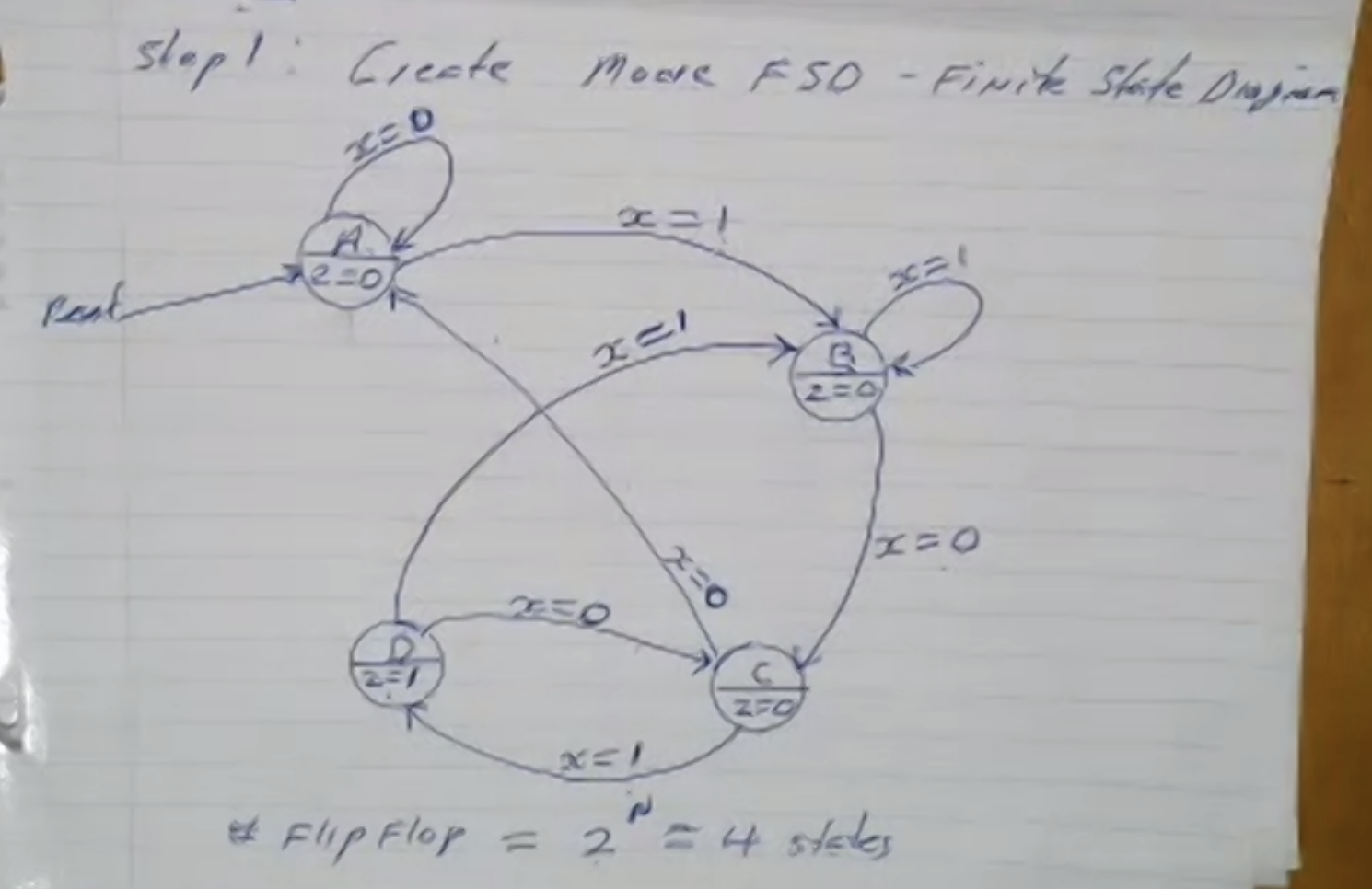
Step 2: determine the minimum number of states/bits required to store states
Number of bits = \( \lceil \log_2(k) \rceil = \lceil \log_2(4)\rceil = 2 \) , where \( k = \text{number of states} \) .
Step 3: From FSD, create the truth table for NSG (next state generator)
We can let our states be represented by binary values:
\( A = 00 \\ B = 01 \\ C = 10 \\ D = 11\)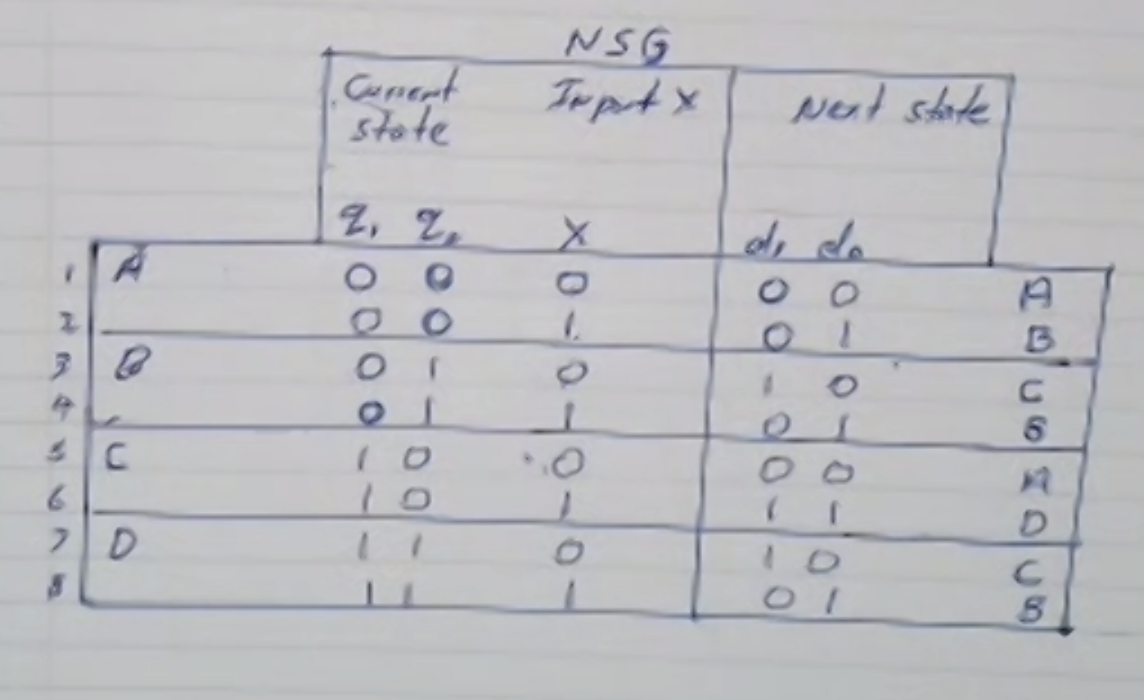
We can create our OG (output generator)
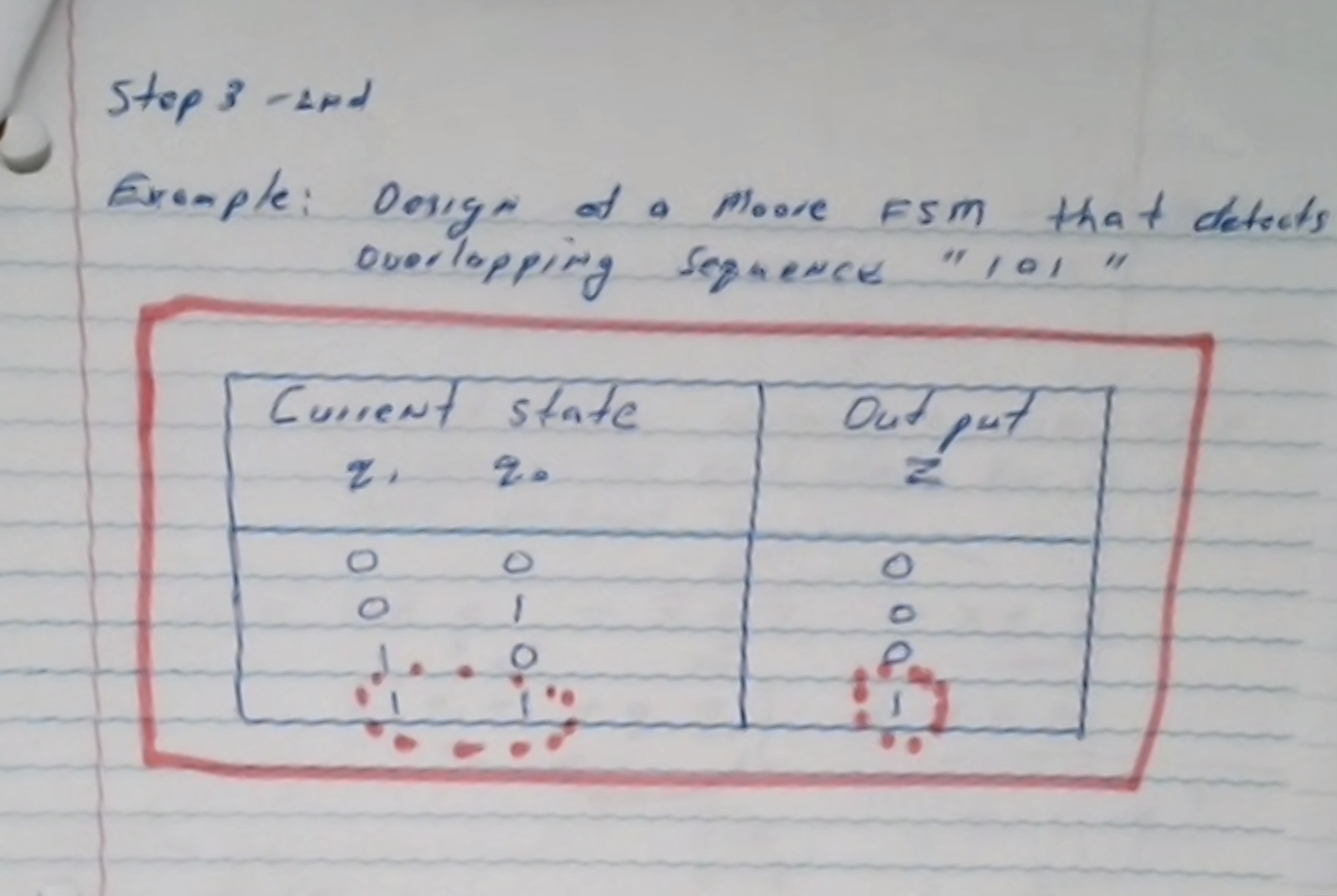
Step 4: Truth table, determine min SOP expression for each state variable \( d_1, d_0 \) and output \( Z \) .
We can start with \( d_0 \) , note that \( d_0 \) is exactly the same as \( x \) .
\[\begin{aligned} d_0 = x \end{aligned}\]Then we can build a SOP for \( d_1 \) (and simplify):
\[\begin{aligned} d_1 &= \overline{x} \overline{q_1} q_0 + \overline{x} q_1 q_0 + x q_1 \overline{q_0} \\ &= \overline{x} (\overline{q_1} q_0 + q_1 q_0) + x q_1 \overline{q_0} \\ &= \overline{x} q_0 + x q_1 \overline{q_0} \end{aligned}\]We can also find the SOP for our output \( Z \) :
\[\begin{aligned} Z = q_0 q_1 \end{aligned}\]