Sequential circuits cont. #
Creating the S-R latch cont. #
| \( S \) | \( R \) | \( Q_t \) | \( Q_{t+1} \) |
|---|---|---|---|
| 0 | 0 | \( Q_t \) | \( Q_t \) |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | Undefined |
\( Q_{t + 1} \) is the "next output."
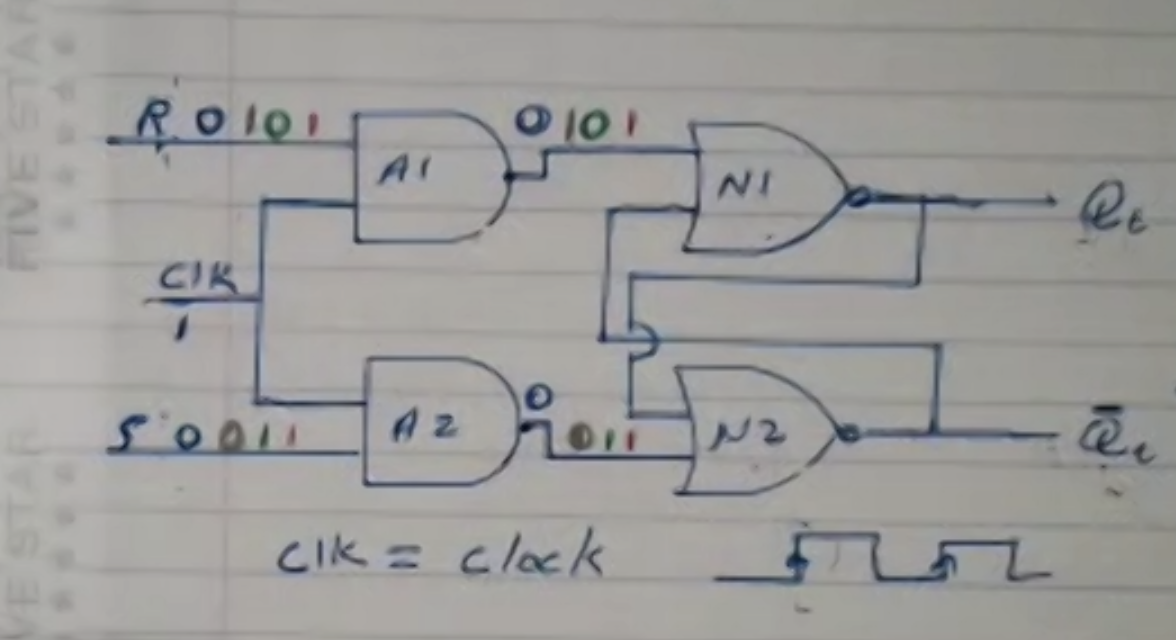
Case 1: \( S = 0 \) , \( R = 0 \)
\[\begin{aligned} Q_{t+1} &= \overline{0 + \overline{Q_t}} = Q_t \\ \overline{Q_{t+1}} &= \overline{0 + Q_t} = \overline{Q_t} \end{aligned}\]Case 2: \( S = 0 \) , \( R = 1 \)
\[\begin{aligned} Q_{t+1} &= \overline{1 + \overline{Q_t}} = \overline{1} = 0 \\ \overline{Q_{t+1}} &= \overline{0 + \overline{Q_t}} = \overline{Q_t} \end{aligned}\]Case 3: \( S = 1 \) , \( R = 0 \)
\[\begin{aligned} Q_{t+1} &= \overline{0 + \overline{Q_t}} = 1 \\ \overline{Q_{t+1}} &= \overline{1 + Q_t} = 0 \end{aligned}\]Case 4: \( S = 1 \) , \( R = 1 \)
\[\begin{aligned} Q_{t+1} &= \overline{1 + \overline{Q_t}} = \overline{1} = 0 \\ \overline{Q_{t+1}} &= \overline{1 + Q_t} = \overline{1} = 0 \end{aligned}\]Since the output and its complement are the same, this case is wrong.