More reduction examples #

Recap on reductions: A reduction is simply a hypothetical algorithm.

ASolver(a)
    ...
    BSolver(...)
    ...

ASolver relies on the existence of BSolver. So ASolver reduces to BSolver. So if BSolver exists, then ASolver exists.

Acceptance problem #

If we have an algorithm accept(m,x), we are wondering if we run the algorithm m on input x, it will either output “accept” or “reject”. The claim is there is no algorithm that can produce this on all inputs (m,x).

The idea of reductions gives us the framework to show that other algorithms cannot exist.

So if we establish that accept(m,x) isn’t computable on all inputs, then we can also show that subroutines that accept may use also don’t exist.

accept(m,x)
    ...
    subroutine(...)
    ...

Since accept reduces to subroutine, subroutine also doesn’t exist.

accept(m,x):
    construct temporary new program m':
        m'(w):
            if w != x:
                output reject
            else
                output m(x)
    output acceptAny(m')

acceptAny(m') outputs “accept” if m' accepts any input.

Lets say that accept is running, and it is passed the algorithm m, and an input x. The first thing it does is create a new program m'. The new program that is created is passed to acceptAny. If m' doesn’t accept anything, it outputs reject on almost everything. The only time that it outputs “accept”, is when m accepts x. acceptAny will be true, if and only if m accepts x. So accept works only if acceptAny works.

Building and interpreting bf parse trees #

We are going to write some Java that parses this grammar:

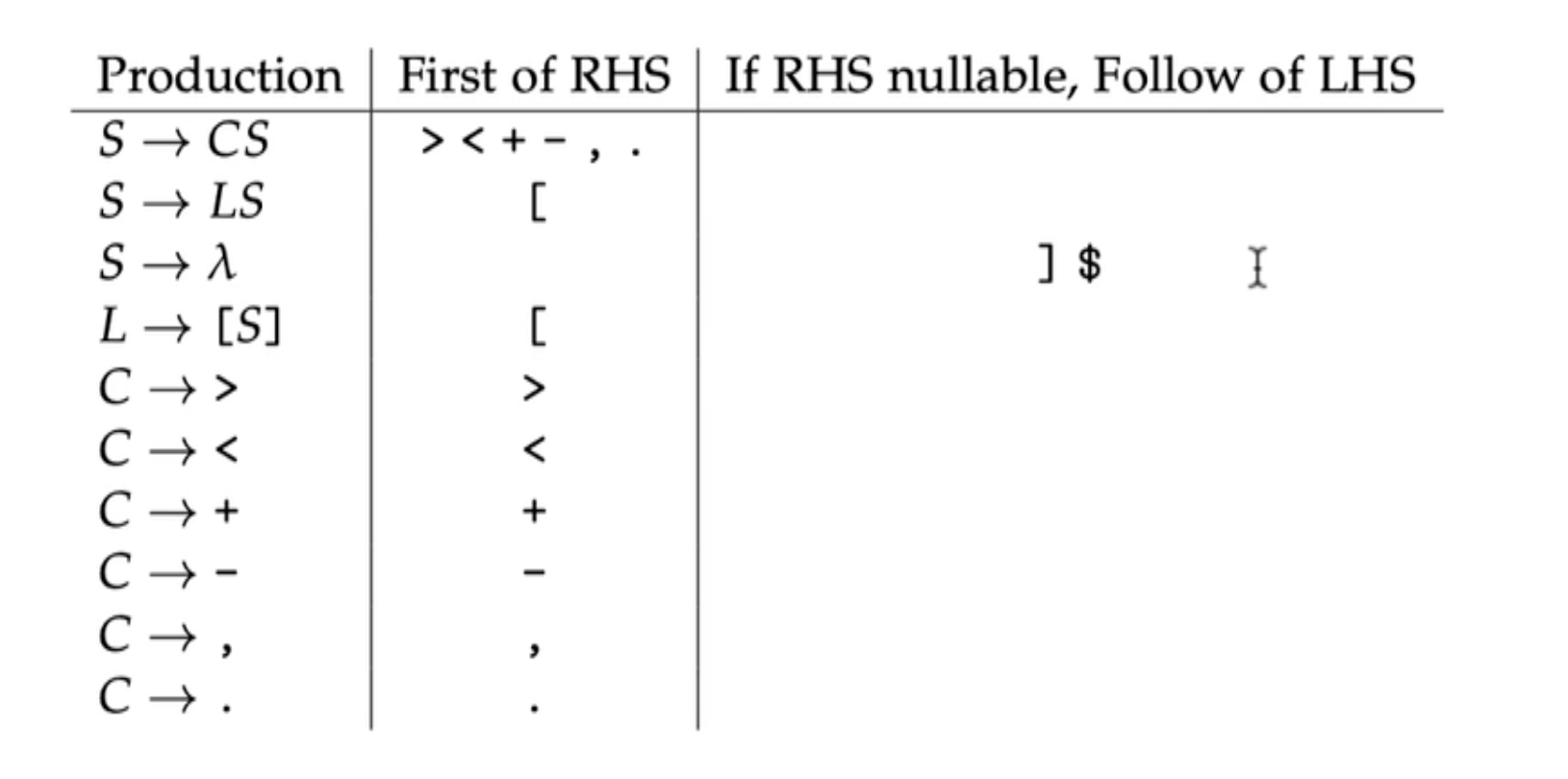
This will be based on our Java parser a couple lectures back.

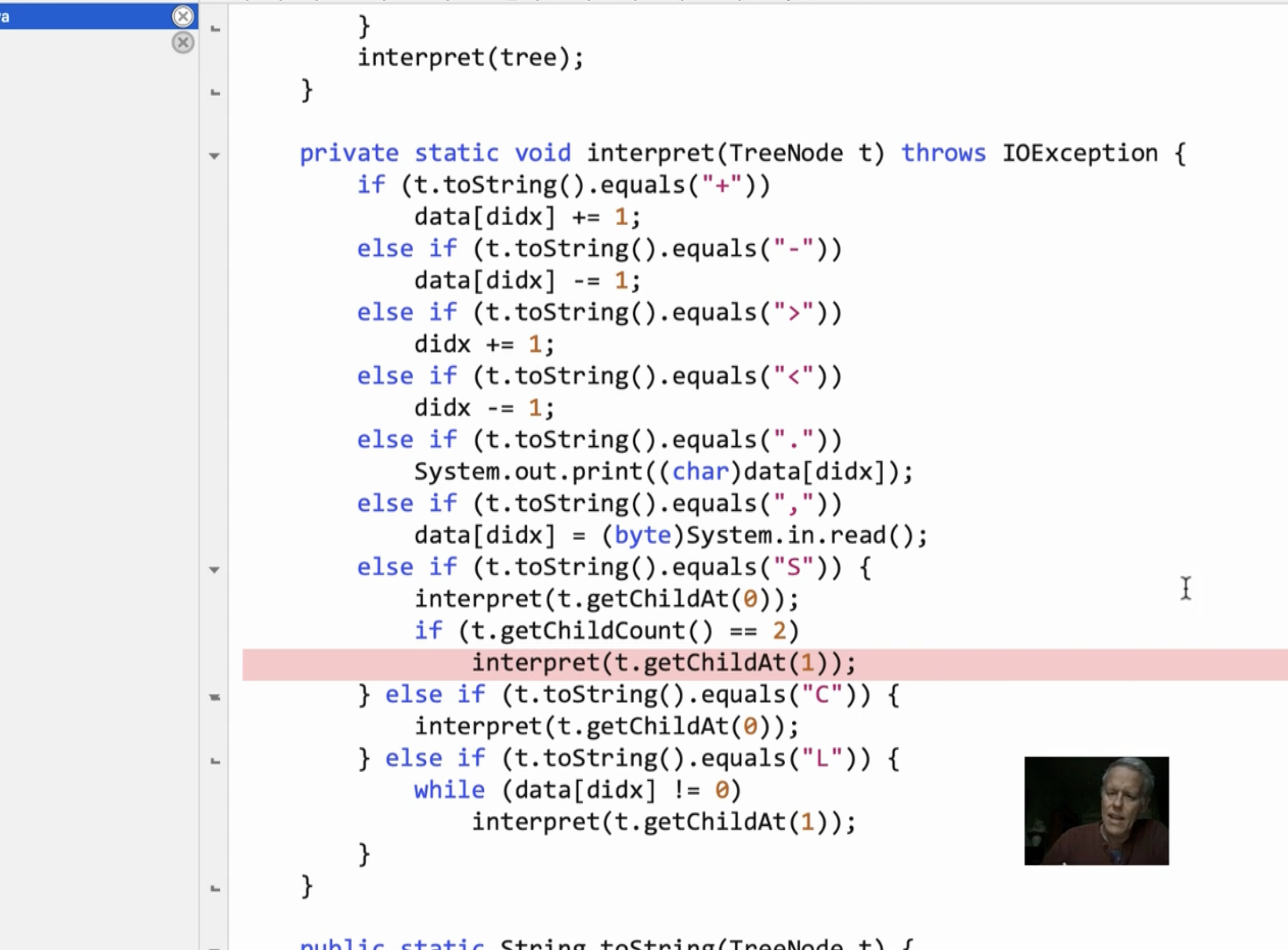
Visualizing the tree for the program:

[..]

This will first follow the production \( S \to LS \)

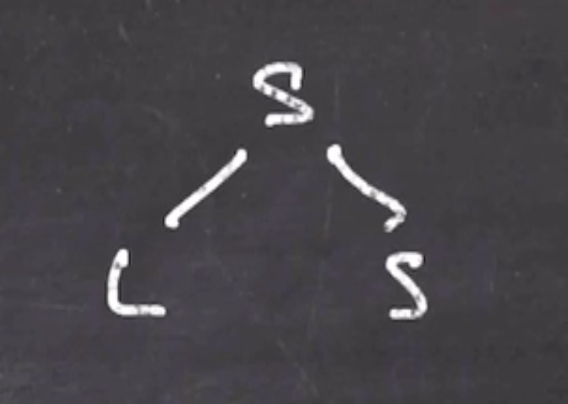
Then we follow the production \( S \to CS \)