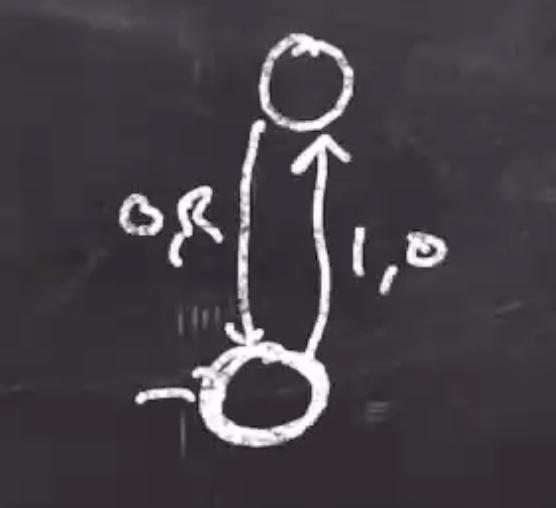Introduction to Turing machines #

Note: See text book readings for formal history of the Turing machine.

A Turing machine has a tape that is infinitely long in both directions. The machine has a tape head that can read and write to the tape.

The control unit of the Turing machine is an automata. Each transition has a pair \( x,y \) , follow the arrow if the tape head is over \( x \) , and do operation \( y \) .

\( y \) can be:

• \( R \) , move right
• \( L \) , move left
• \( y \) , write \( y \) , can be a blank (indicated by \( B \) ).

Turing machines are deterministic, and have no \( \lambda \) transitions. The machine halts when no transition matches, so Turing machines don’t require a transition for every alphabet character.

There are two types:

• Recognizer, which accepts/rejects input.
• Transducer, which takes input and produces output.

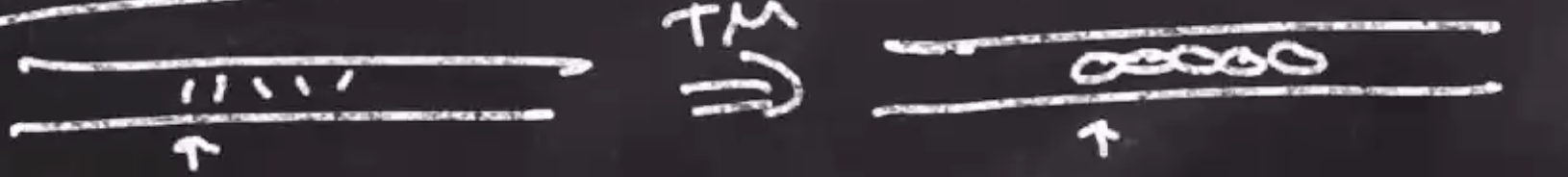
By convention, the tape head always starts at the far left of the input, and ends at the far left of the output.

First example #

With a tape starting with \( n \) 1s, we want the output to be \( n \) 0s.

Some simple pseudo code might be

while head is over 1
    write 0
    move R
move L
while head is over 0
    move L
move R

Make sure to check edge cases, i.e. only a single 1 being on the tape. Also check if the tape is empty initially.

This starts out as a self loop on the initial state that has the pair \( 1,0 \) .

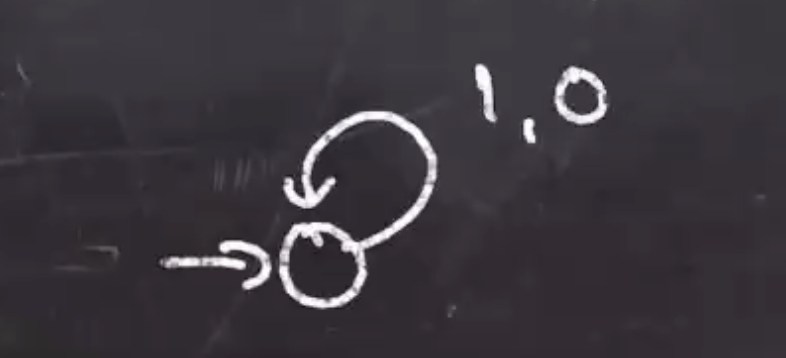
The move R can be added as another pair \( 0,R \) .

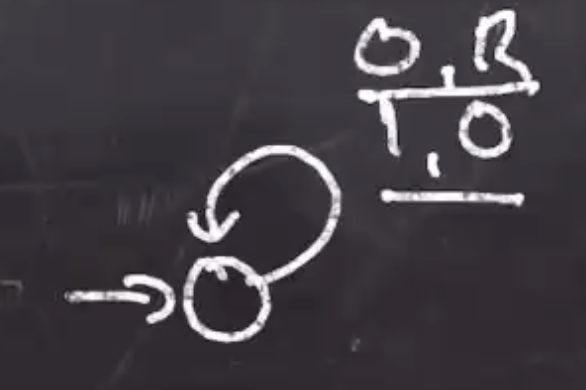
Note: This would be a problem if we had any 0s in the input to begin with, we are assuming the input is good. To handle this we could have a state like

Which would halt on a 0 in the initial input.

When this loop finishes, it means we are no longer over a 1. The head should be over a blank. So to transition to the next state we have the pair \( B,L \) .

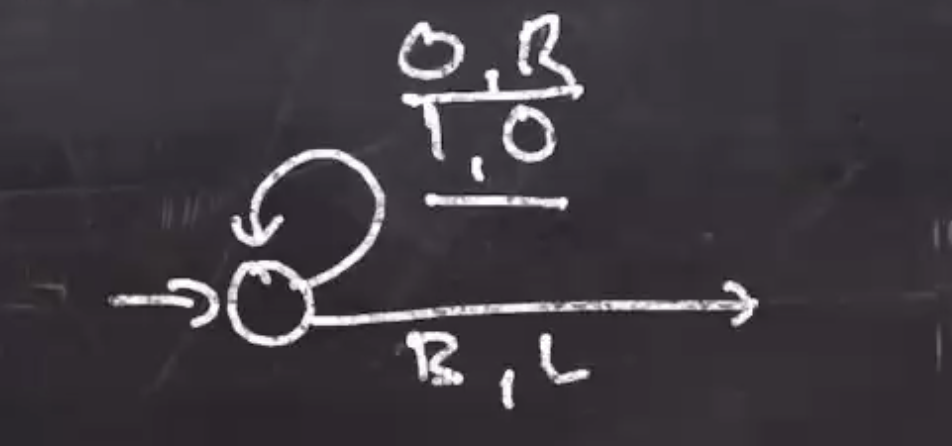
The next loop can be handled by \( 0,L \) . And when we reach the far right blank we can move right.

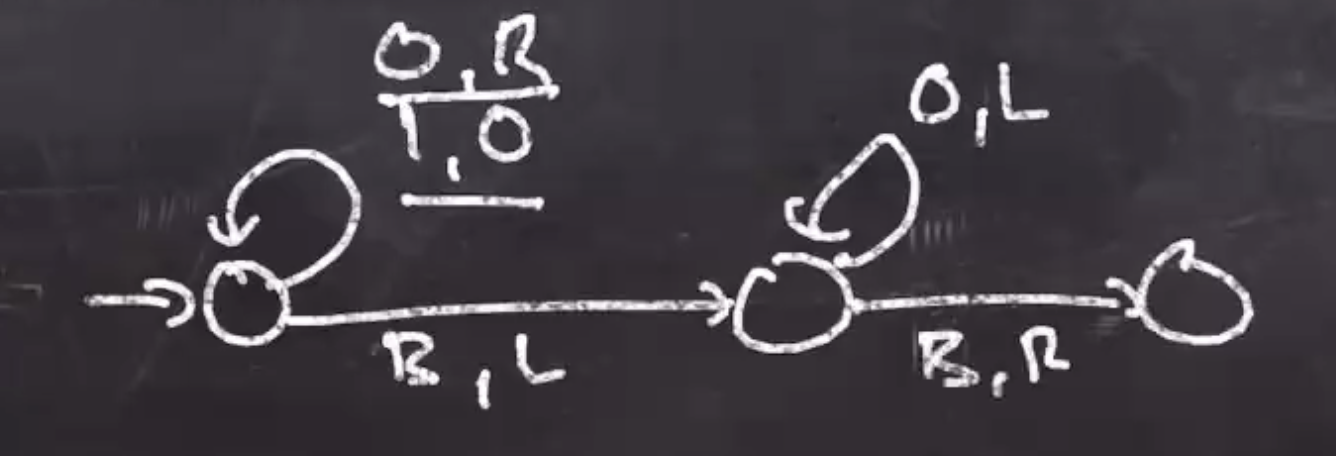
The last state has no arrows, so the program will halt.

Second example #

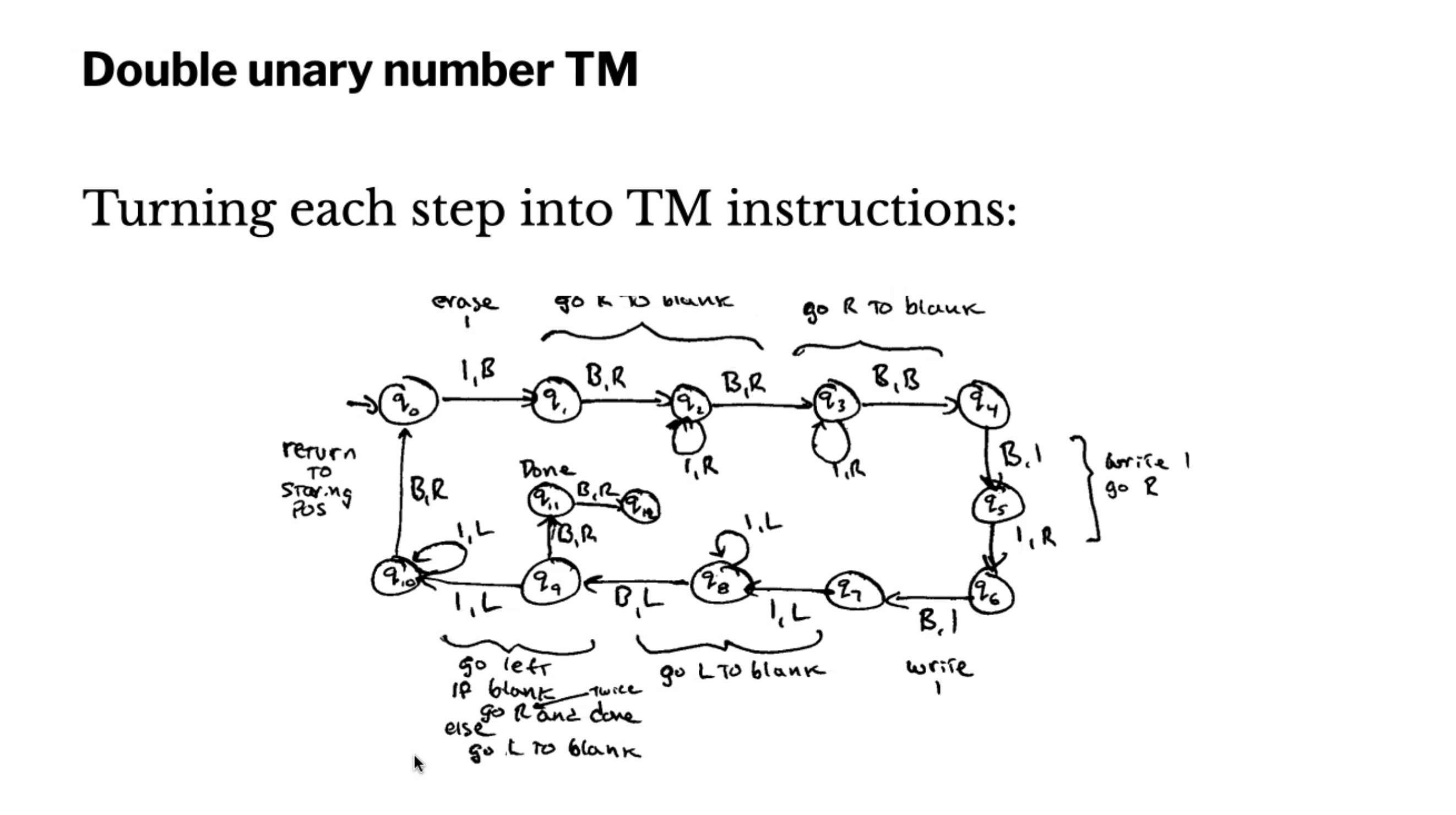
The pair \( B,B \) is kind of like “no operation”.

Testing #