Pumping lemma for CFL #

PL for RL

Given \( RL, L \) there exists \( p \) such that if \( w \in L \) and \( |w| \geq p \) then there exists \( w = xyz \) where

• \( |y| > 0 \)
• \( |xy| \leq p \)
• \( xy^iz \in L \)

We consume \( w \) and we get to a state that is the first repeated state. At some point we come back to it, and then to the accept.

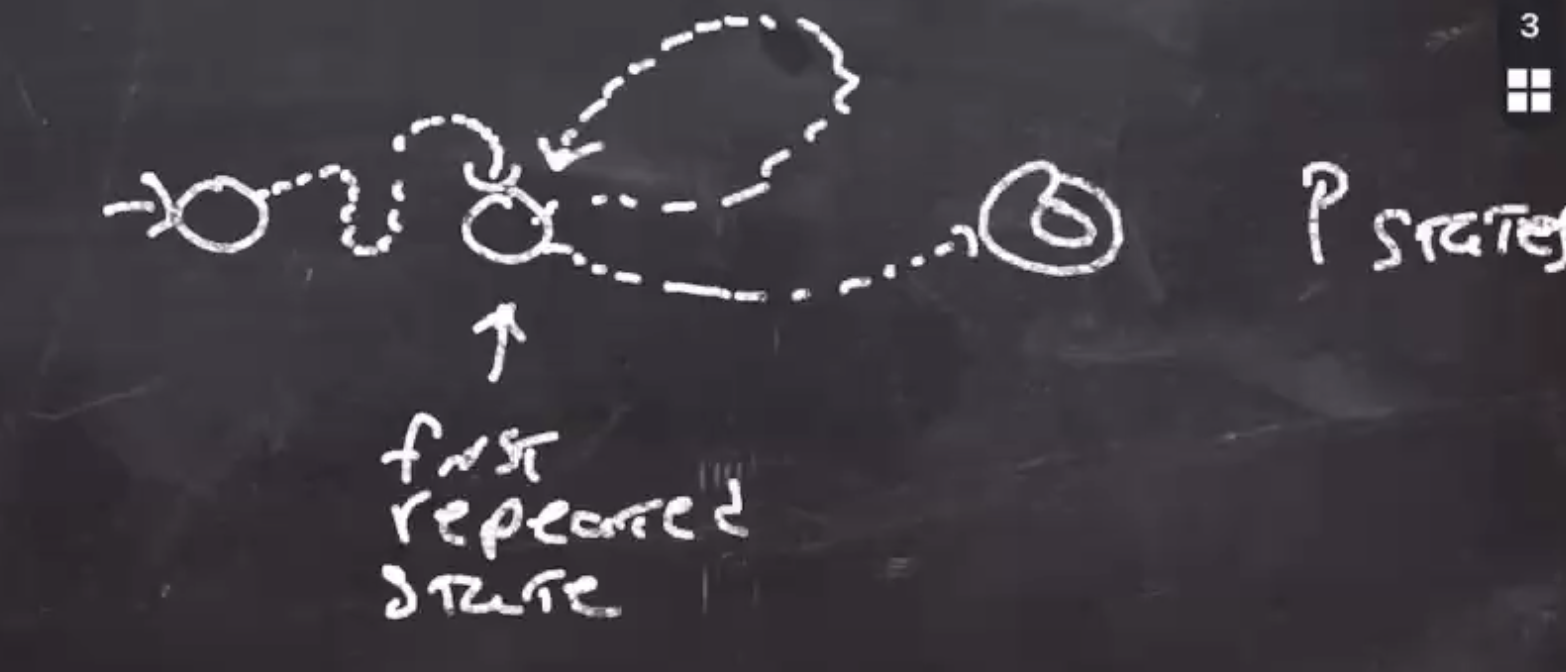
Since \( w \) is \( p \) or longer, it must visit one state more than once. We can identify this state as the one we get repeated. The part that gets us there the first time \( x \) , the part that gets us there the second time \( y \) , and the part that goes to the accept state \( z \) .

If \( x \) gets us to the repeated state, then we can go around \( y \) as many times we want (or omit).

Proof template #

Given context-free language \( L \) , there exists \( p \) such that if \( w \in L \) and \( |w| \geq p \) , then there exists a \( w = uvxyz \) where

• \( |vy| > 0 \)
• \( |vxy| \leq p \)
• \( uv^ixy^iz \in L \)

Main use: we look for strings that are in the language and at least \( p \) long, and then apply the pumping lemma to show that the language is not context-free.

To prove:

• Assume \( L \) is context-free
• Pick \( w \in L \) with \( |w| \geq p \)
• Argue that the pumping lemma says that there exists \( w = uvxyz \) with
  • \( |vy| > 0 \)
  • \( |vyx| \leq p \)
  • \( uv^ixy^i \in L \)
• Argue that either if we pump down ( \( i = 0 \) gives us \( uxz \) , or if we pump up \( i > 0 \) we get \( uvvxyyz \) and show that \( e \not \in L \)
• Pumping lemma says string is in \( L \) , contradiction, so \( L \) is not context-free.

Example #

Consider \( L = \{a^n b^n c^n : n \geq 0\} \)

This starts by consuming \( a \) ’s and pushing them onto the stack. Then when we start seeing \( b \) ’s we pop the \( a \) ’s off. When we reach the \( c \) ’s we don’t have a way to remember how many \( a \) ’s or \( b \) ’s we saw.

Note: A Turning machine can do this because it has 2 stacks.

So lets prove its not context-free using the pumping lemma.

The string we pick must be length \( p \) and exist in \( L \) :

\( w \) exists in the language and is at least \( p \) long (it is in fact \( 3p \) long).

So lets assume that this language is context-free, and apply the pumping lemma.

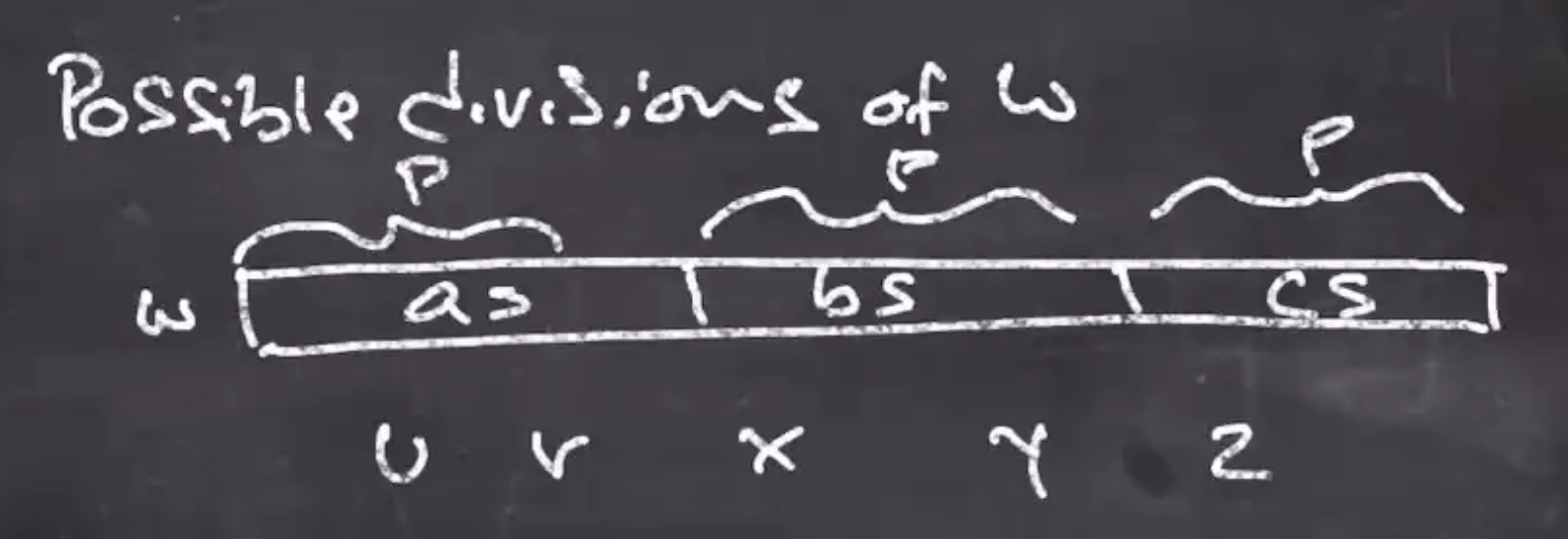
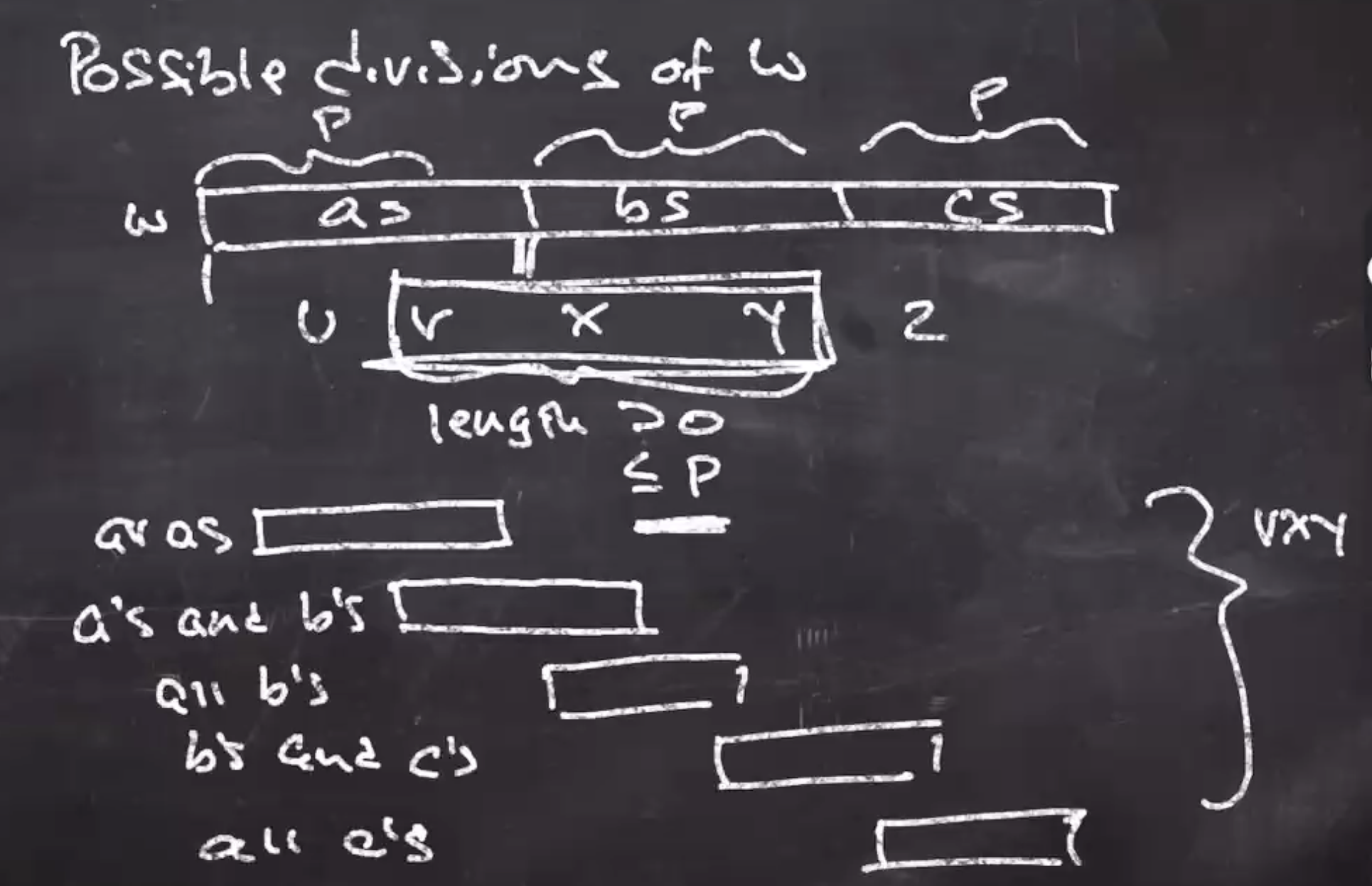
Possible divisions for \( w \) :

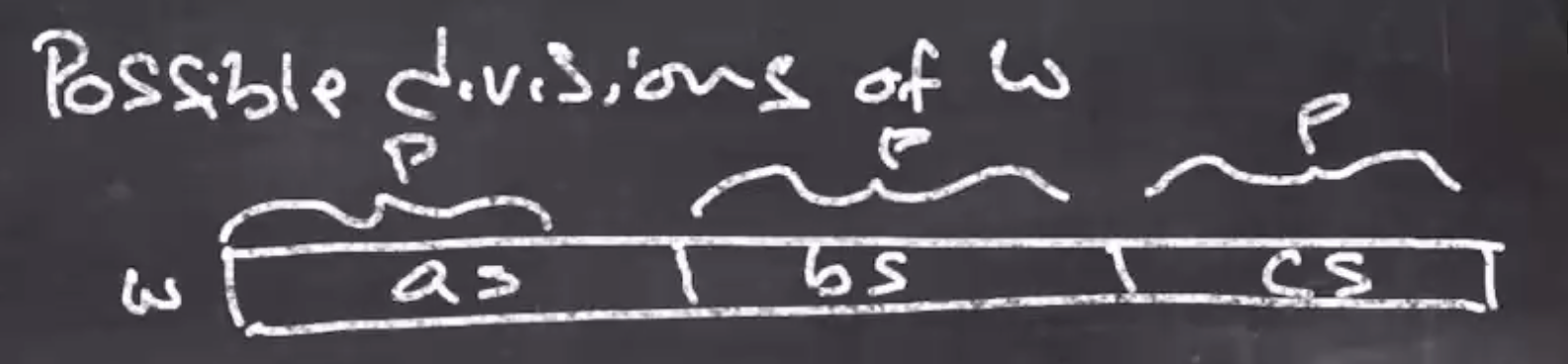
Since \( w = uvxyz \) , we don’t know exactly where they are however

We do know that \( 0 < |vxy| \leq p \)

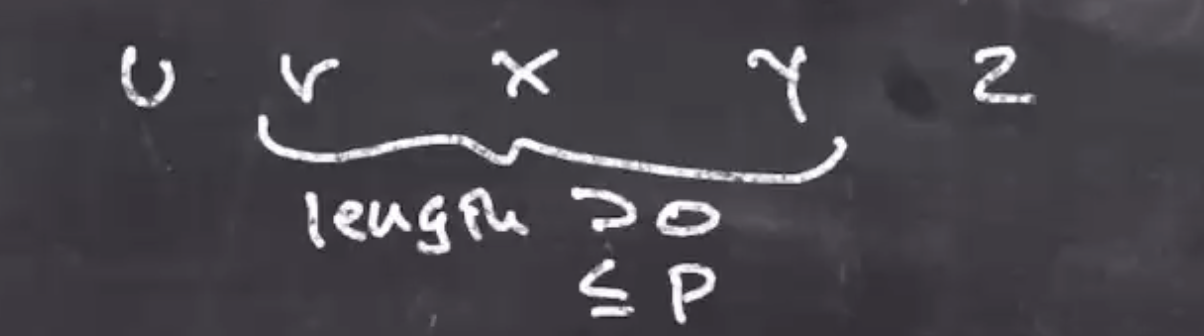
Its possible that \( vxy \) :

• appear in the region of just \( a \) ’s, since there are at least \( p \) \( a \) ’s. So \( vxy = \) all \( a \) ’s.
• appear in the \( a \) ’s and \( b \) ’s.
• any other combination of 2, but not all 3

So, \( uvvxyyz \) will increase 1 or 2 types of characters, but not all 3. Thus it is out of balance, and the string is not in \( L \) .

Therefore, the language \( L = \{a^n b^n c^n : n \geq 0\} \) is not context-free.

Why the pumping lemma is true #

If \( L \) is context-free, then there is a context-free grammar for it. So, every string \( w \in L \) has a parse tree:

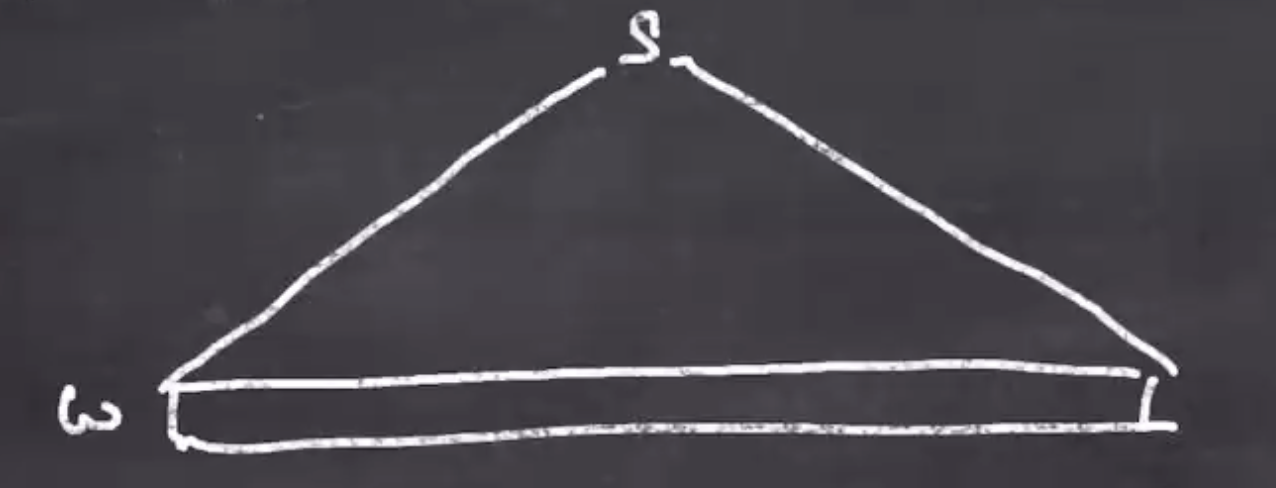
where the fringe is \( w \) and the interior is non-terminals.

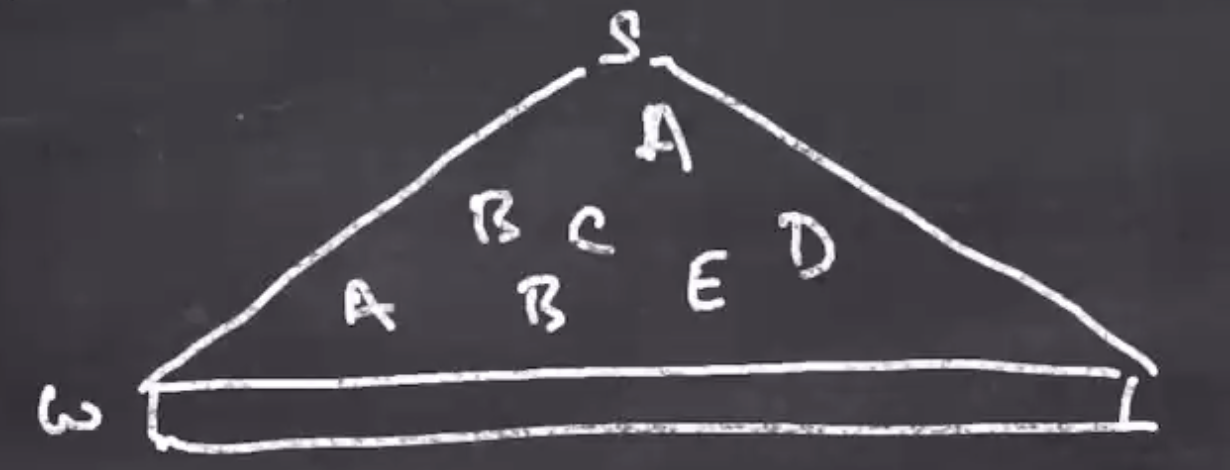
Observe,

• The longer that \( w \) is, the taller the tree
• The taller the tree, the more non-terminals in the longest root-to-leaf path
• Once the root-to-leaf path is long enough, some non-terminal must repeat in it

There are a finite number of productions in the grammar, and so as the tree gets longer and longer until there must be a repeat. This is where the pumping lemma comes in.

As an abstraction:

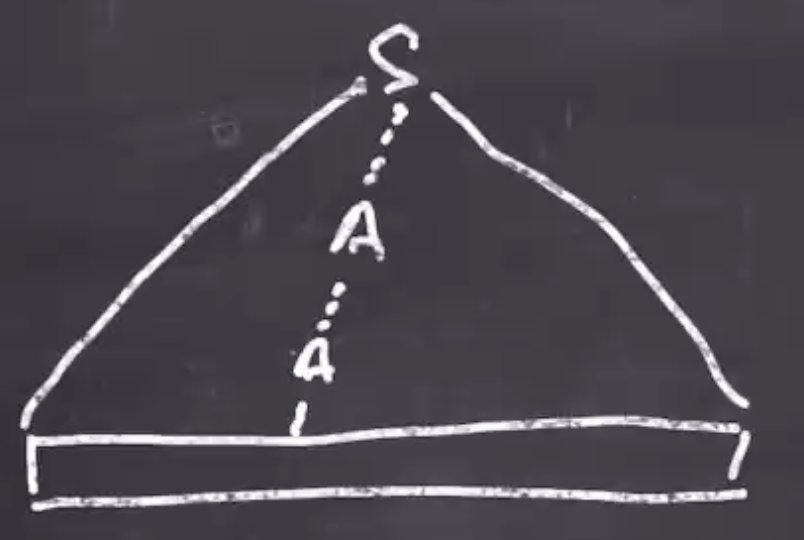
Some part of \( w \) will be derived from \( A \) .

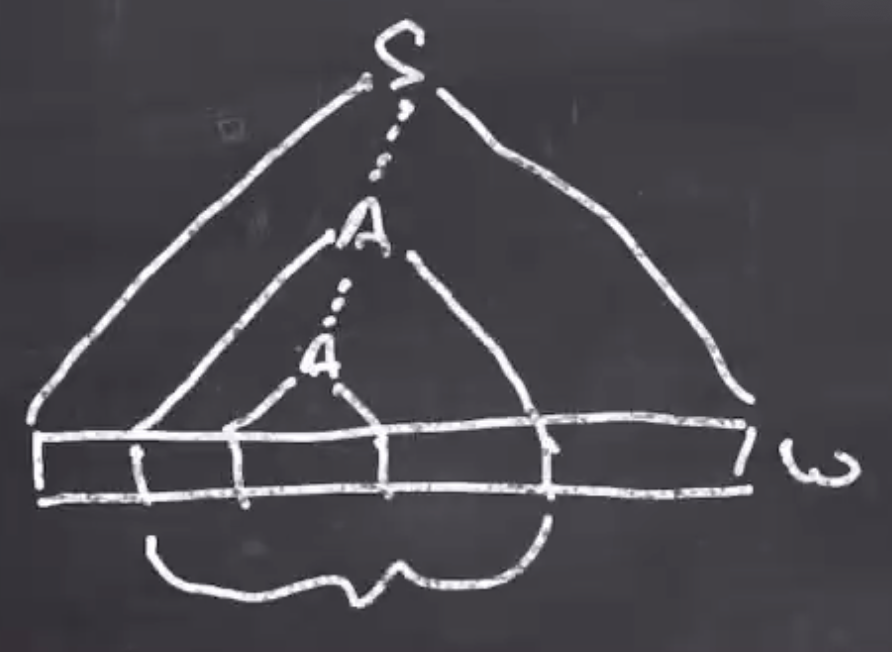
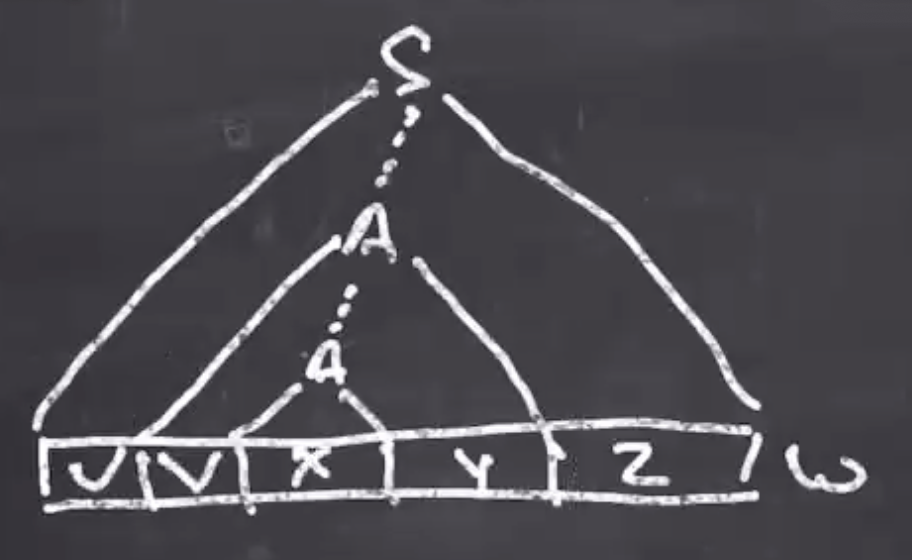
This tells us that

• \( x \in L(A) \) , and
• \( vxy \in L(A) \)

So each time that \( A \) is reached, we can replace it with \( x \) or \( vxy \) , we can pump the \( v \) and \( y \) as many times we want.

Note: This is similar to the pumping lemma for regular languages because it also uses the pigeon hole principle.