Context-free grammars #
Recall, for regular languages: regular expressions are generators, and finite automata are recognizers. Context-free grammars are the recognizers of context free languages.


Any string we can make in this process is in the language. Any string we can’t make in this process is not in the language.




So \( \{a^n b^n: \text{n is integer}\} \) is context free. Remember, we couldn’t describe this language using regular expressions because finite automata don’t have memory.
Designing context-free grammar #
Consider the previous example’s language: \( \{a^n b^n: \text{n is integer}\} \)
\(S \to aSb \\ S \to \lambda\)If we wanted the language \( \{a^n b^{2n}: \text{n is integer}\} \)
\( S \to aSbb \mid \lambda\)If we want to have a language that decides one string from class \( A \) and one string from class \( B \) :
\( S \to AB \\ A \to aA \mid \lambda \\ B \to bB \mid \lambda\)Another pattern we see occasionally is one that sequences things, in different stages.
For the language \( \{a^n b^m c^r: n, m, r \text{ are integers}\} \)
\( S \to aS \mid T \\ T \to bT \mid R \\ R \to cR \mid \lambda\)So it first takes strings from stage \( S \) , then stage \( T \) , then \( R \) .
So a derivation of \( a^2b^2c^2 \) would be:
\( S \to aS \to aaS \to aaT \to aabT \to aabbT \to aabbR \to aabbcR \to aabbccR \to aabbcc \)An example designing a CFG #
Consider the language \( L = \{a^l b^m a^n : l,m,n > 0, l+n=m\} \) , for example the strings \( abba, aabbba, abbbaa \) have the same number of \( a \) ’s and \( b \) ’s.
Every substitution must introduce one \( a \) and one \( b \) to be matched.
We can think of 2 classes \( T \) and \( R \) .
\( S \to TR \\ T \to aTb \mid \lambda \\ R \to bRa \mid \lambda\)This adds \( a \) ’s and \( b \) ’s in a one to one fashion, so this guarantees there will be the same amount.
However, note that the empty string can be derived:
\( S \to TR \to R \to \lambda \)So we can fix our CFG to:
\( S \to TR \\ T \to aTb \mid ab \\ R \to bRa \mid ba \\\)So the shortest string derived is now:
\( S \to TR \to abR \to abba \)Solving the same example using a PDA #
Recall the language \( L = \{a^l b^m a^n : l,m,n > 0, l+n=m\} \)
To create a push-down automata for this language we follow these steps:
- Consume \( a \) ’s and push
- Consume \( b \) ’s and match them with \( a \) ’s (pop the \( a \) off the stack when we consume a \( b \) ).
- Consume \( b \) ’s and push
- Consume \( a \) ’s and pop \( b \) ’s
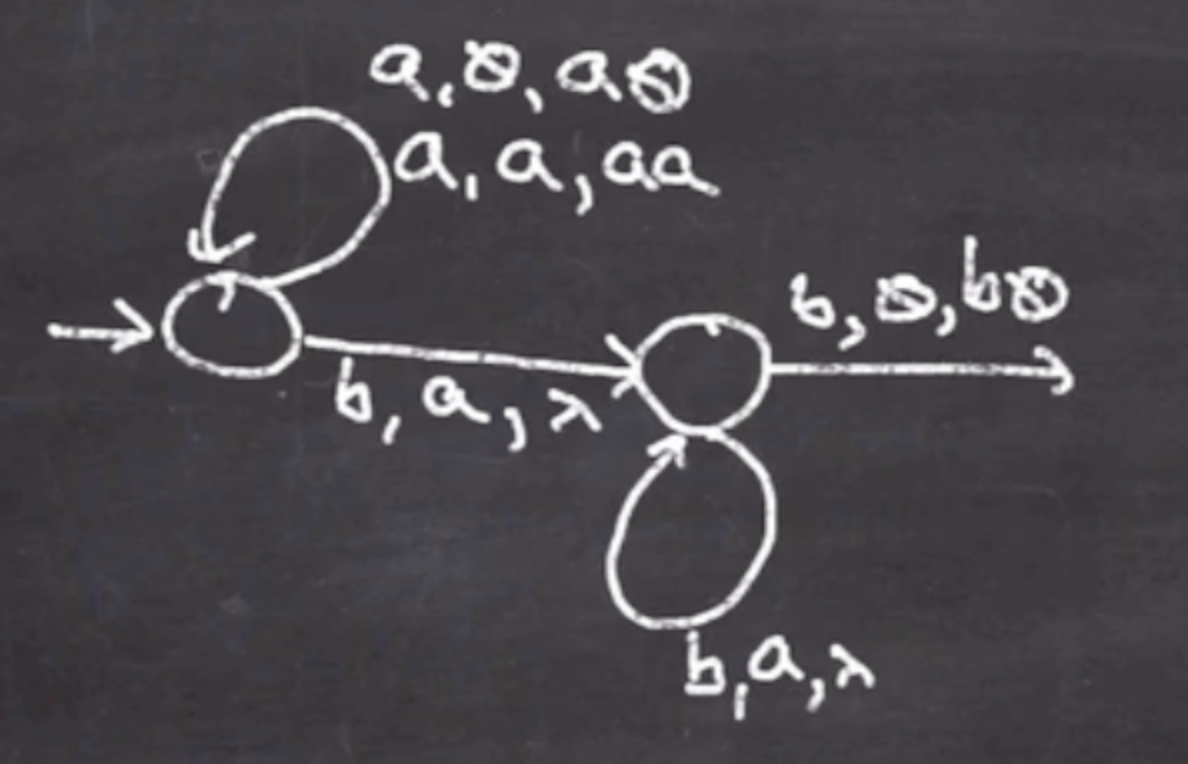
The arrows are labeled as char to consume, top of stack, what to push from right to left:
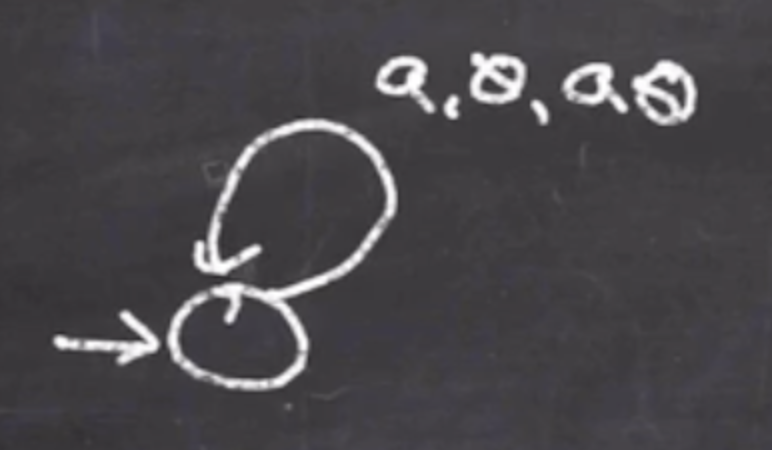
So this handles the first \( a \) , so we can add:
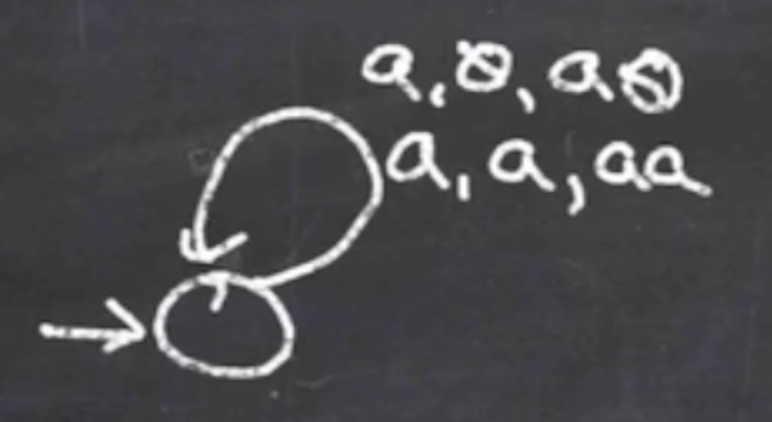
Now we handle the \( b \) and pop \( a \) :
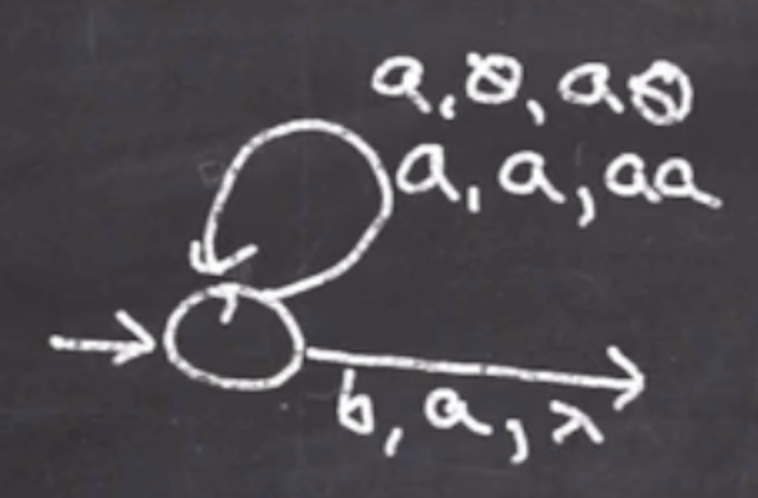
Now there will be more \( b \) ’s, so we can self loop off the new state:
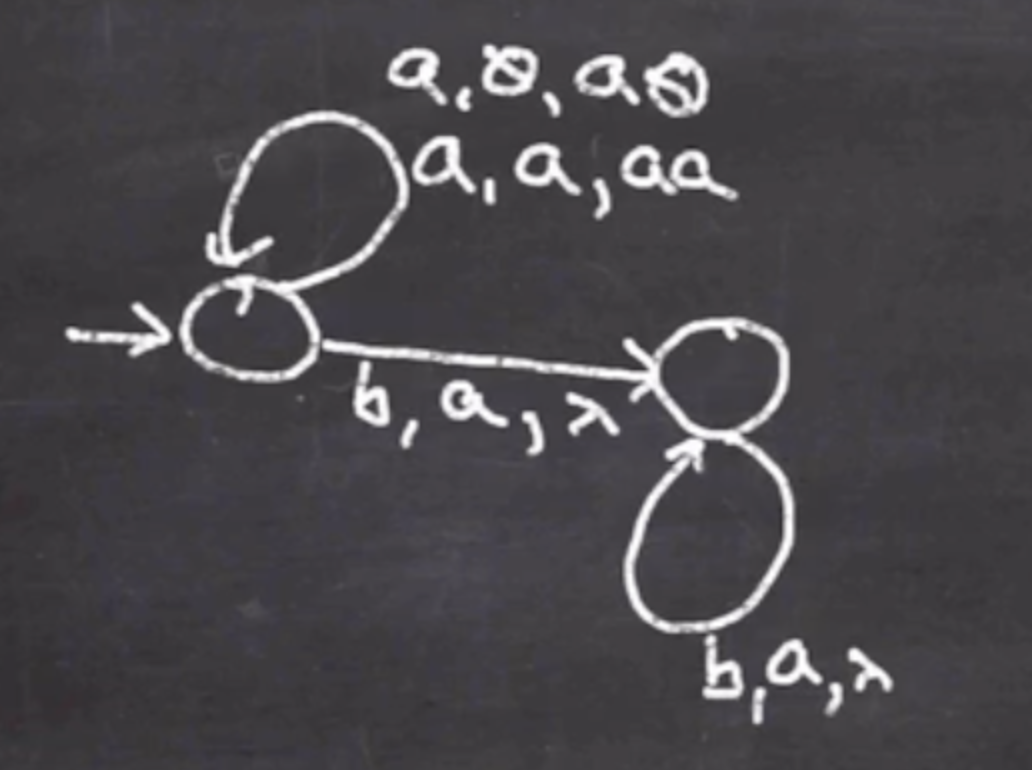
We need to consume more \( b \) ’s and push them onto the stack:
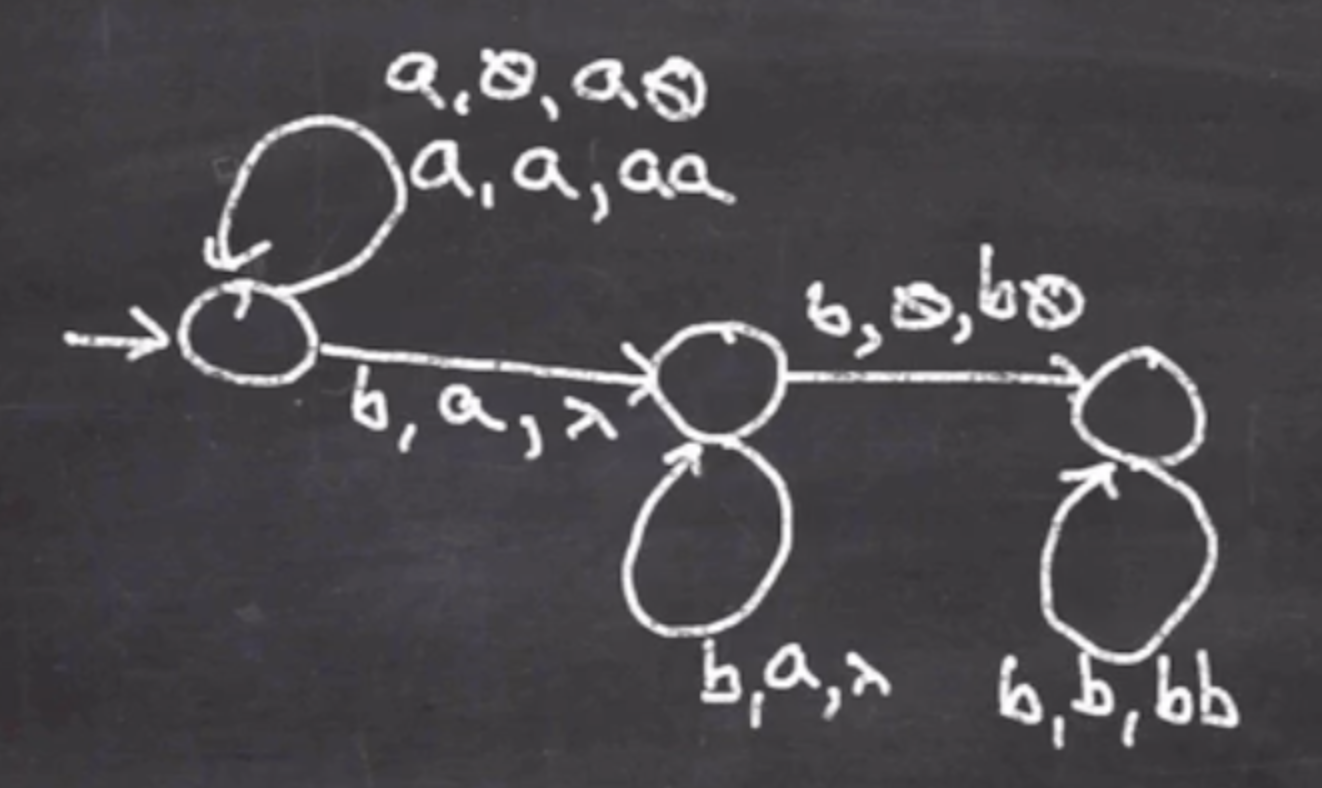
And finally handle the last \( a \) ’s and pop \( b \) ’s.
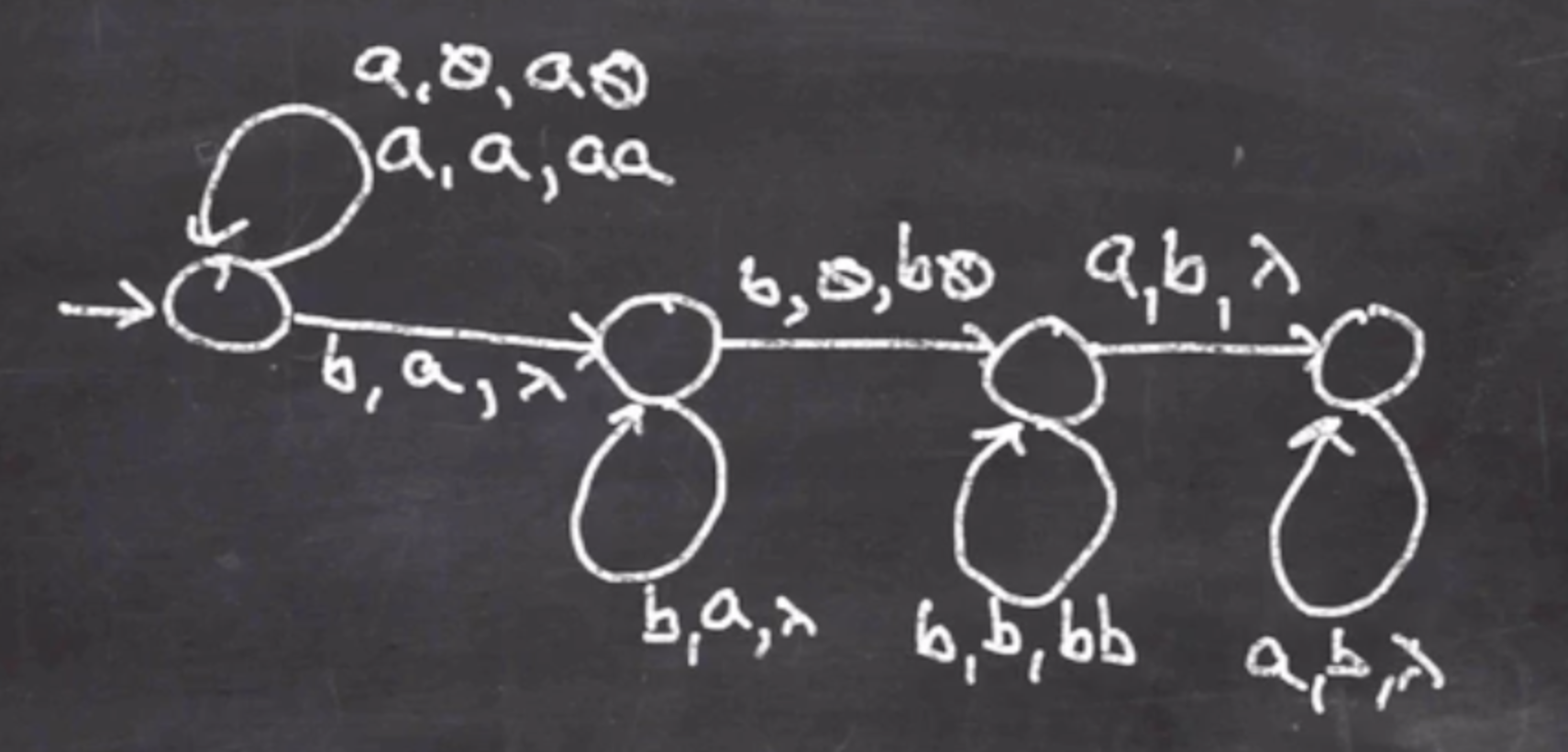
So this will go on, and if we have nothing on the stack then it is an accept.
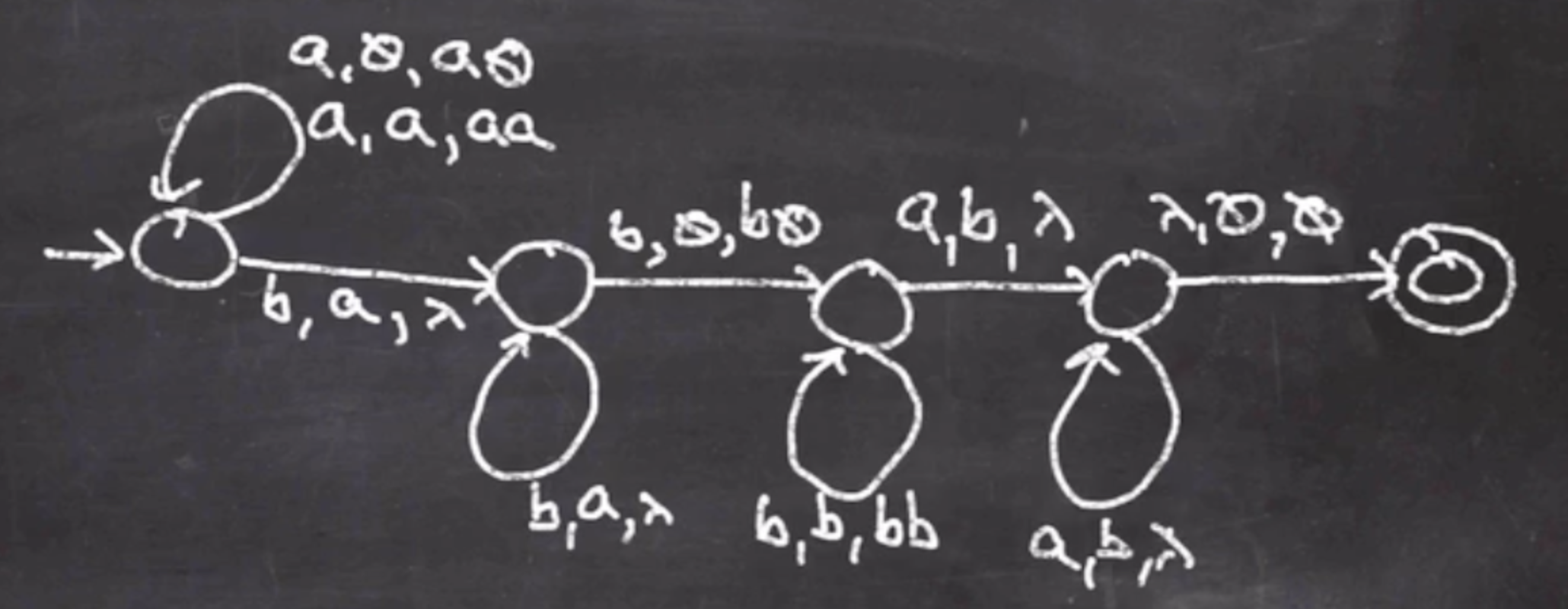
You can only follow the last arrow if the stack is empty.
Tip: when designing these push-down automatas, think of the algorithm first (the steps above).
Odd length palindromes #
Consider the language \( L = \text{odd length palindromes} \) over the alphabet \( \{a,b\} \) . Note that the empty string will not be accepted. There will always also be a center character.
So some of the strings accepted will be \( \{a, b, aaa, aba, bab, bbb, aaaaa, aabaa, ...\} \) .
So lets come up with the CFG:
\( S \to aSa \mid bSb \mid a \mid b\)Note: if we added a \(\lambda\) to this definition, it would describe all palindromes.
Lets derive \( ababa \) :
\( S \to aSa \to abSba \to ababa\)So for the push-down automata, lets think of the algorithm first:
- Consume and push first half of string
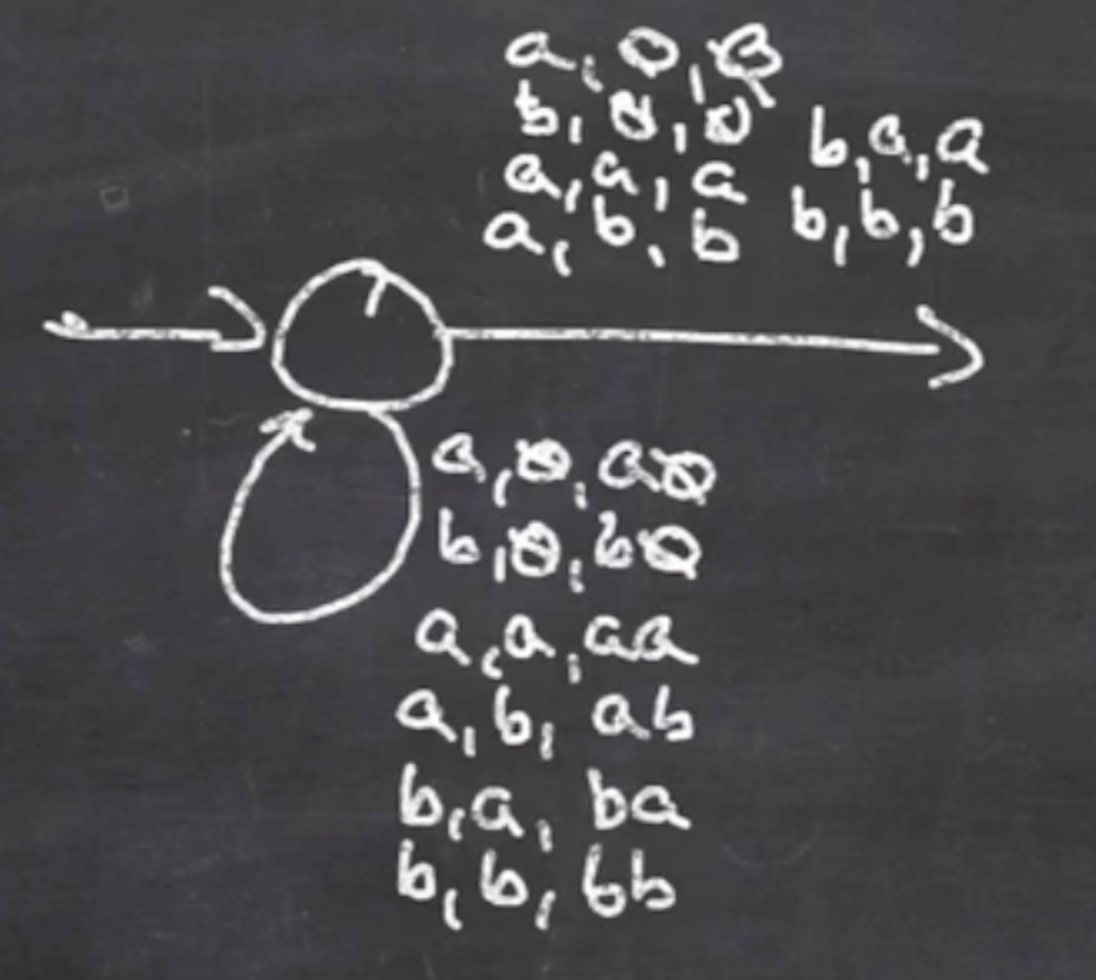
- Consume the middle char
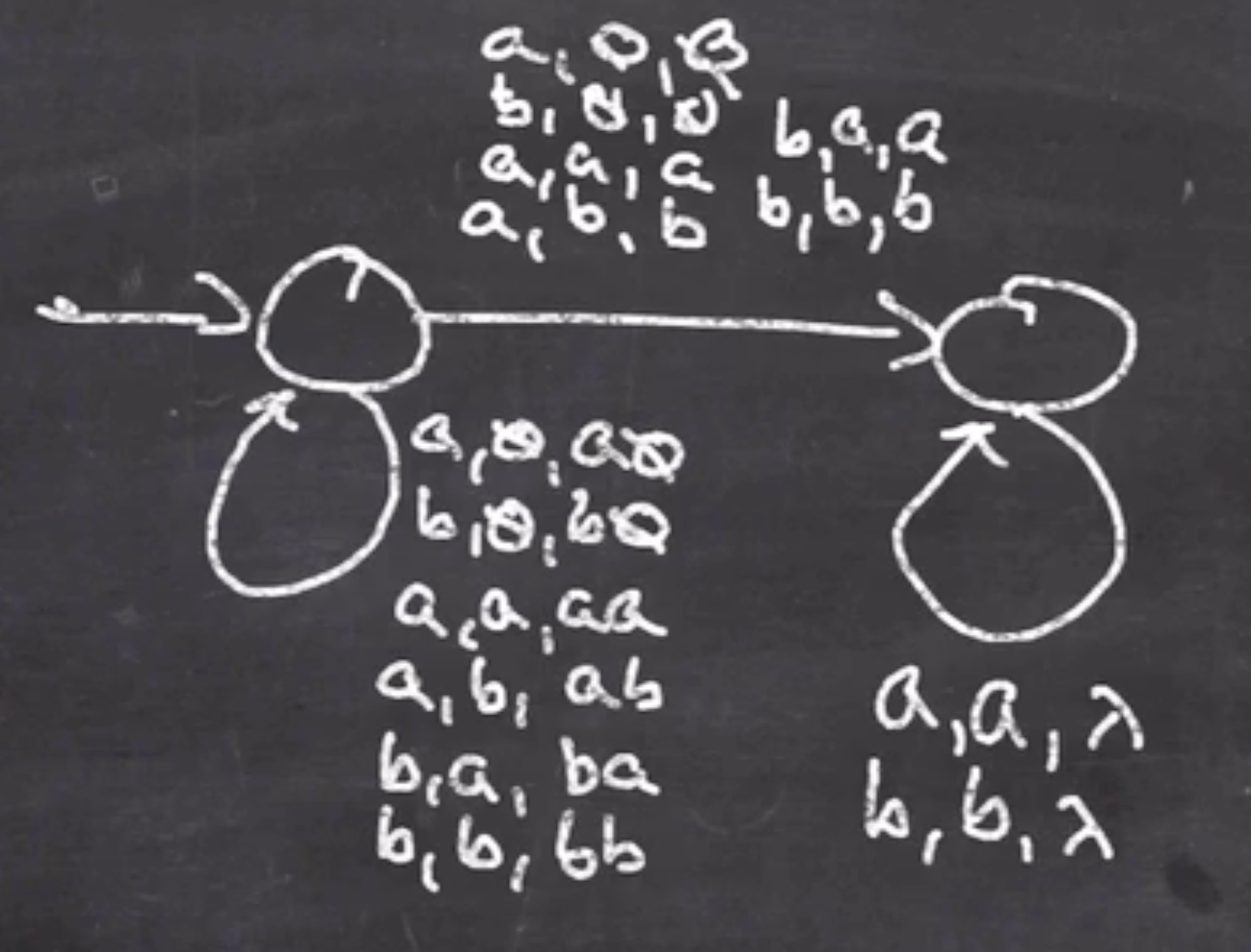
- Consume and pop the second half of the string
- Check that stack is empty
So how do we know when we get to the middle? The middle can be either of our alphabet chars. Without a special char in the middle, there will be non-determinism in this push-down automata. In this case, non-determinism does give the push-down automata more power.
So lets start with step 1:
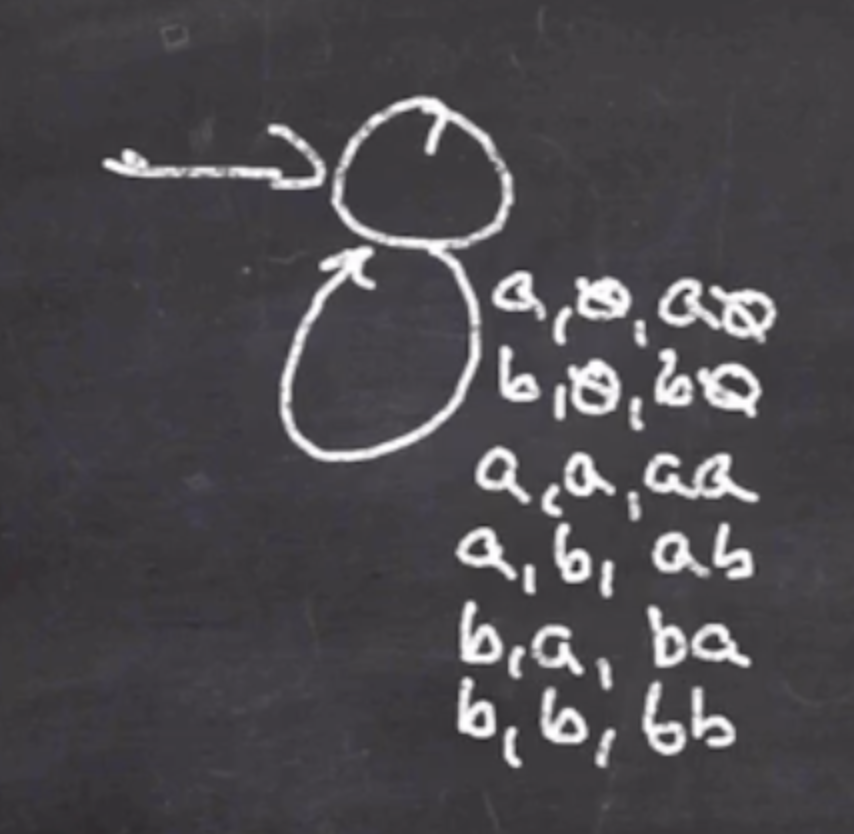
Then we’ll encounter the middle character, step 2:
Now we can consume the next input and see if it matches, step 3:
Finally check if the stack is empty, step 4:
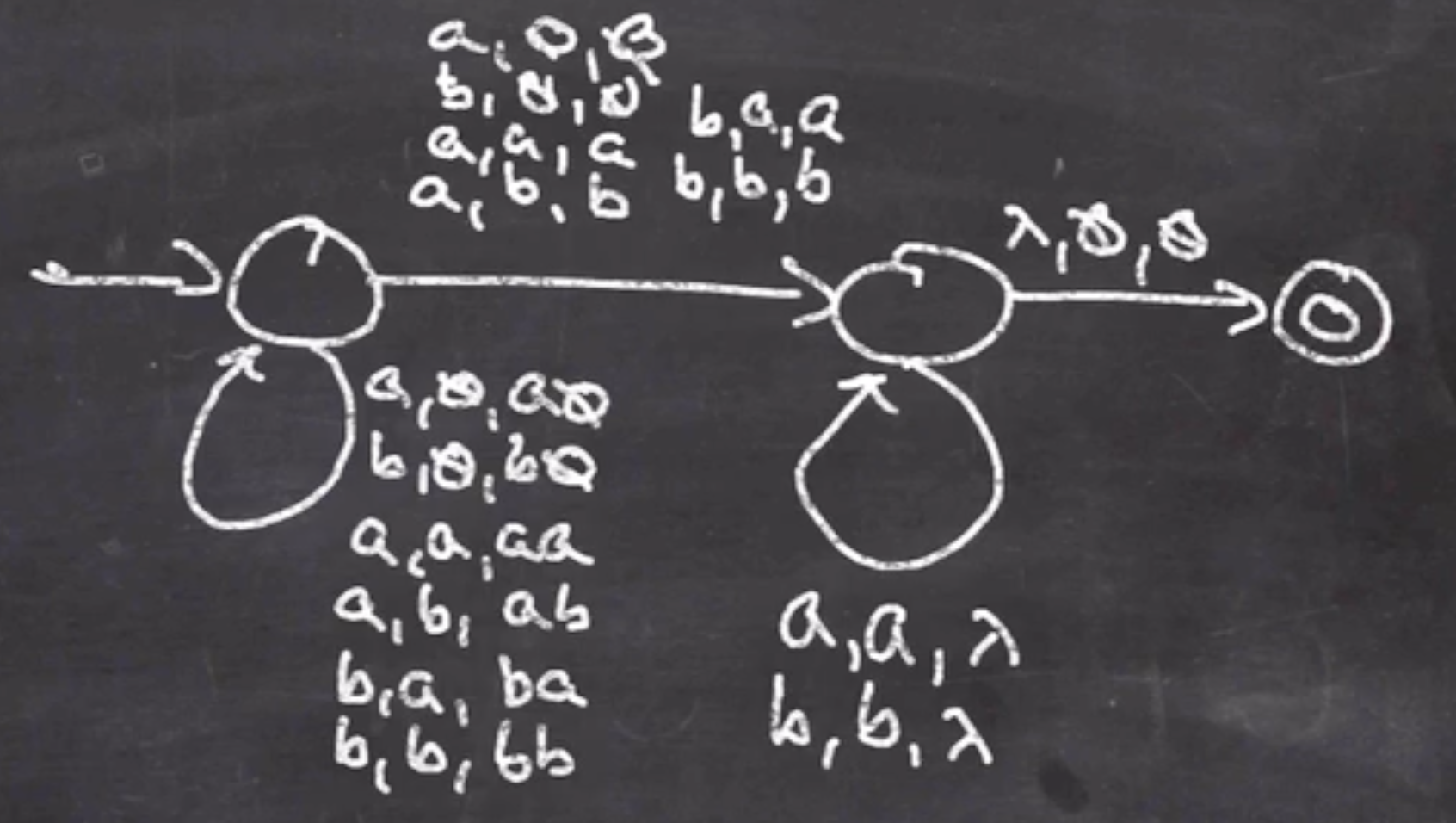
We can only get to the accept state if the stack is empty.