Mergesort in Racket #

Mergesort breaks the list in half and sorts each half recursively.

Some pseudo:

ms(list)
    front = front half of list
    back = back half of list
    ms(front)
    ms(back)
    return merge(front, back)

In racket, there is a function called drop that takes a list and a number. It drops the numbers off the list. There is also take, that takes the first number of elements of the list and returns them.

(define list '(1 2 3 4 5 6))            ; helper definition
(drop list 2)                           ; '(3 4 5 6)
(take list 2)                           ; '(1 2)
(drop list (quotient (length list) 2))  ; drops the first half of the list

So we can start our mergesort definition:

(define (ms xs)
    (if (< (length xs) 2)
        xs
        (merge (ms (take xs (quotient (length xs) 2)))
               (ms (drop xs (quotient (length xs) 2))))))

However, we haven’t defined merge yet, so:

(define (merge xs ys)
    (cond ((empty? xs) ys)
          ((empty? ys) xs)
          ((< (first xs) (first ys)) (cons (first xs) (merge (rest xs) ys)))
          (else (cons (first ys) (merge (rest ys) xs)))))

So we can test this:

(ms '(5 3 6 2 7 1 4))                   ; '(1 2 3 4 5 6)

Higher-order functions #

Treat functions as first class data. We’re going to allow functions to be passed as parameters. We’ll consider 3 functions that take functions as parameters.

• (map f xs) – applies f to each element of xs, and builds a list from the results
• (filter f xs) – f is a boolean, it applies f to each element of xs and filters out any element for which f is false
• (foldl f acc xs) – abstracts the acumulator process we did earlier. It applies f to each value of xs and integrates that value into the accumulator acc. The l in foldl means that it is going from left to right. foldl is \( O(n) \) .

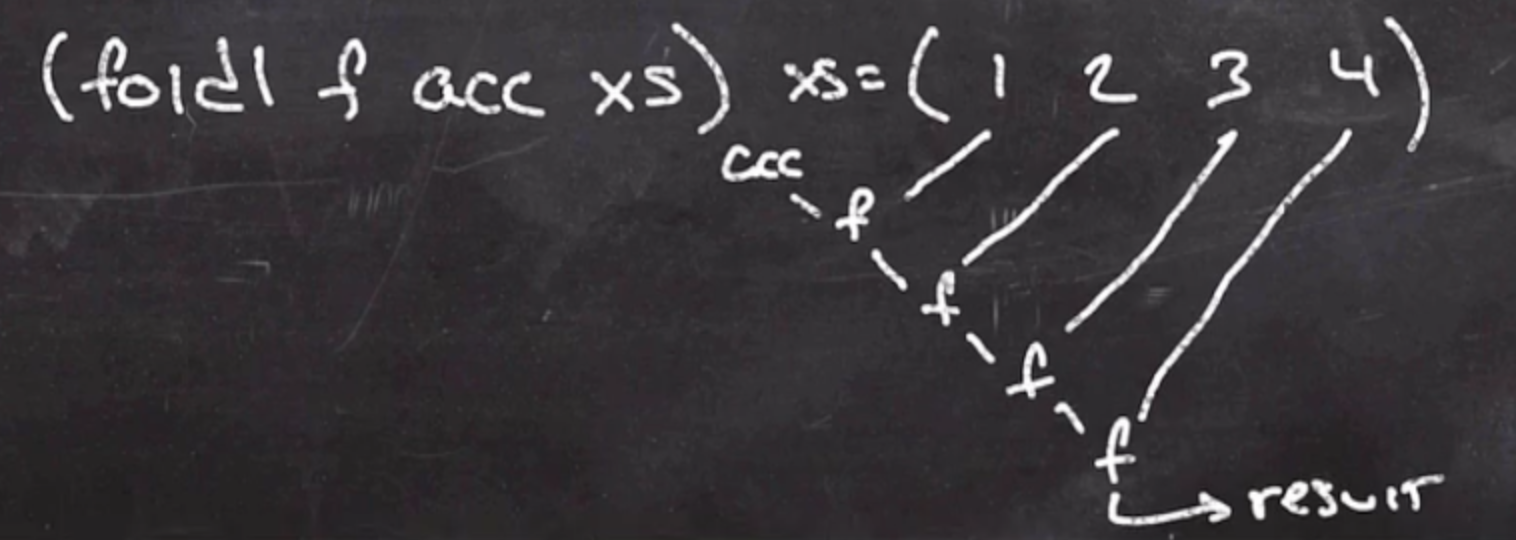
For example, to sum the elements of a list using foldl:

(foldl + 0 xs)                          ; 10

Examples using map:

(map add1 '(1 2 3 4))                   ; '(2 3 4 5)

We can use our own functions in map

(define (double x)
    (+ x x))

(map double '(1 2 3 4))                 ; '(2 4 6 8)

Lets take a look at filter:

(filter even? '(1 2 3 4 5))             ; '(2 4)

Designing filter #

The base case is the empty list, which returns back the empty list. When we are calling the function recursively, we will have to use rest.

Heres a screenshot using even? as f:

; my-filter applies f to each element of xs
; and builds a list from those that make f true
; f: A --> boolean
; xs: list of A
(define (my-filter f xs)
    (if (empty? xs)
        empty
        (if (f (first xs)) ; remember f is a function
            (cons (first xs) (my-filter f (rest xs)))
            (my-filter f (rest xs)))))

So:

(my-filter even? '(1 2 3 4 5))          ; '(2 4)

Designing foldl #

Recall

(foldl + 0 '(1 2 3 4))                  ; 10

; f: (A, B) --> A
; acc: A
; xs: list of B
(define (my-foldl f acc xs)
    (if (empty? xs)
        acc
        (my-foldl f (f acc (first xs)) (rest xs))))

So lets test it:

(my-foldl + 0 '(1 2 3 4))               ; 10

Lambda functions #

Lambdas are nameless (anonymous) functions.

(lambda (x y)
    (+ x y))

How can we call this function if it doesn’t have a name? There are many uses, we can define an operation without writing the full definition.

For example, to double all the numbers of a list:

(define (double-all xs)
    (if (empty? xs)
        empty
        (cons (* 2 (first xs)) (double-all (rest xs)))))

(double-all '(1 2 3))                   ; '(2 4 6)

But we can do this with higher order functions:

(define (double x)
    (* 2 x))

(define (double-all2 xs)
    (map double xs))

(double-all2 '(1 2 3))                  ; '(2 4 6)

Notice that we had to define our doubling function. This is where anonymous functions come in. Their main use is for one time application for a simple functions in a higher order situation.

(define (double-all3 xs)
    (map (lambda (x) (* 2 x)) xs))

(double-all3 '(1 2 3))                  ; '(2 4 6)

Another lambda example #

Lets write a function that keeps the numbers 1 thru 100.

(define (keep-1-100 xs)
    (filter (lambda (x) (and (> x 0) (< x 101))) xs))

(keep-1-100 '(1 -1 -10 50 99 100 101))  ; '(1 50 99 100)

Returning a function using a lambda #

; g(f(x))
(define (composer g f)
    (lambda (x)
        (g (f x))))

We can test out this function:

; using double function from earlier
(define double-add1 (composer add1 double))

(double-add1 10)                        ; 21

Expanding the keep-1-100 function #

If we want to expand our 1-100 function to take any range, we can use lambdas. We can make a higher order function that creates a tester for a specific interval.

(define (interval-factory x y)
    (lambda (z)
        (and (< x z) (> y z))))

This returns a customized function based on the values we pass x and y. We can define the 1-100 interval like so:

(define in-1-100 (interval-factory 1 100))
(in-1-100 50)                           ; #t
(in-1-100 150)                          ; #f
(filter in-1-100 '(-1 1 2 99 100 101))  ; '(2 99)

; another interval
(define in-50-1000 (interval-factory 50 1000))
(filter in-50-1000 '(-1 1 2 99 100 101)); '(99 100 101)

Functional closure #

Return an object that has copies of values in the current scope.

Graphical pseudo:

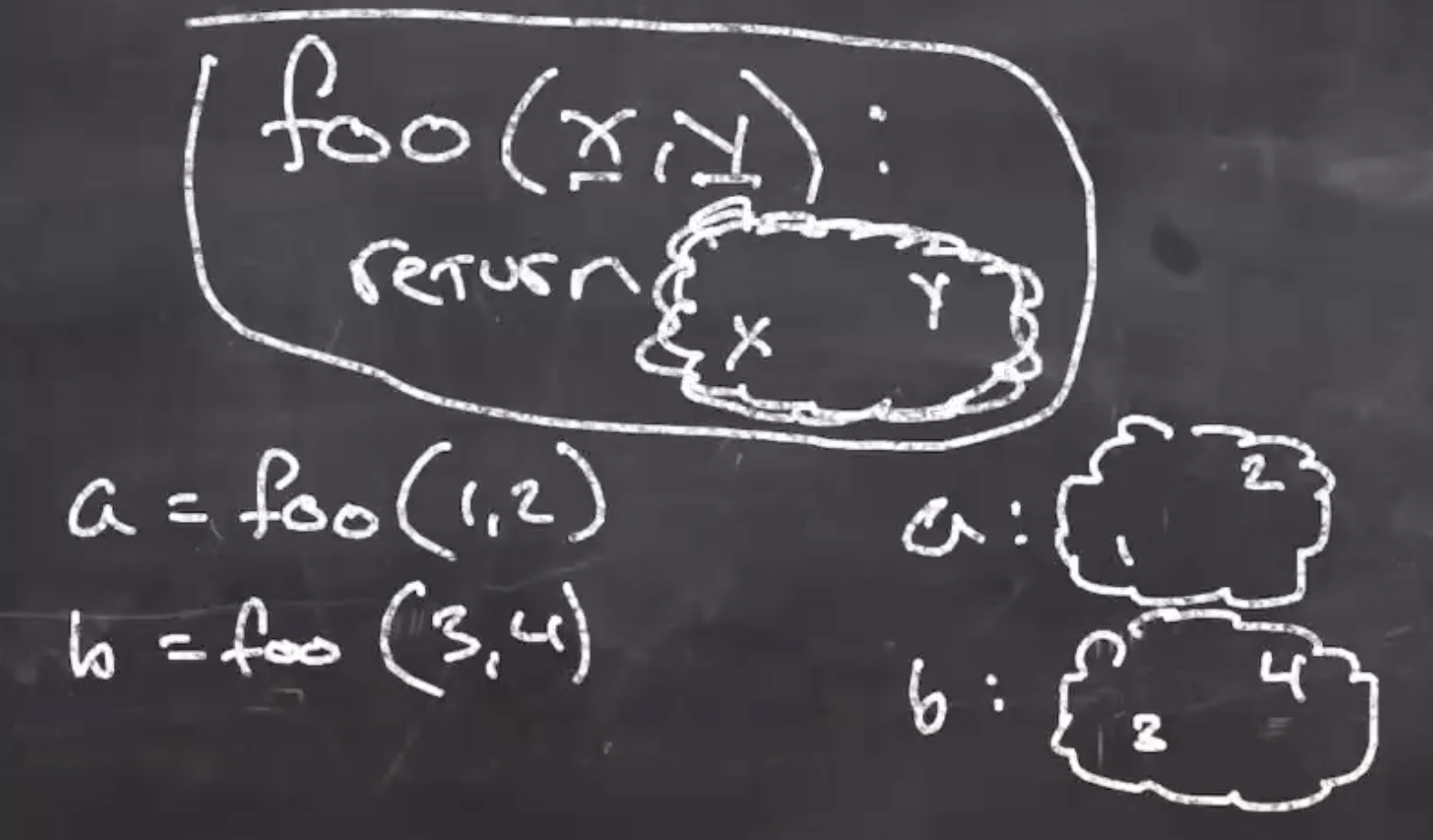
This is the idea of a closure. In the definition of foo, we are constructing an object that copies the current value of x and y. If x and y change it would change the returned object, so we make a copy.

We did this earlier when we defined interval-factory. When we passed in certain values it copies those and returns an object with those values embedded.