http://krovetz.net/135/module_reg/fa_design.html
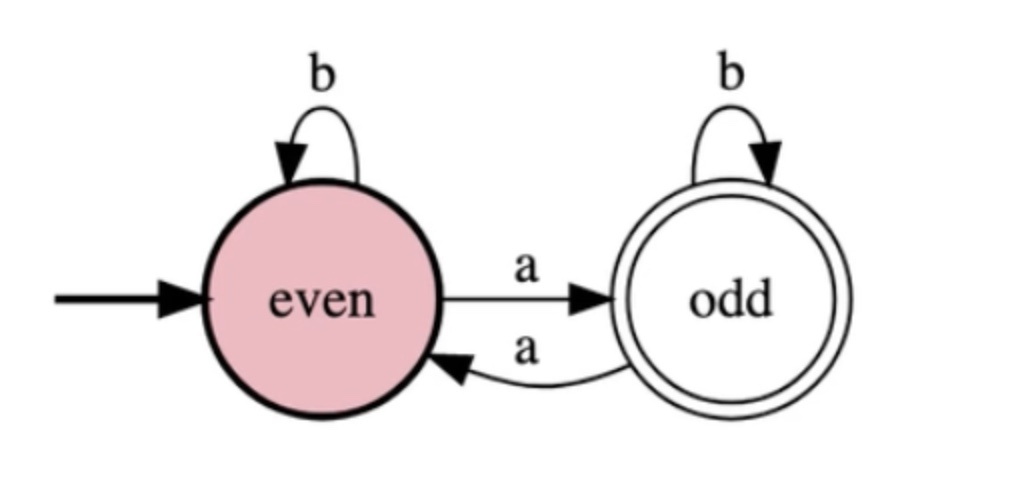
This FSM keeps track of whether there are an even or odd number of a’s.
#alphabet
a
b
#states
even
odd
#initial
even
#accepting
odd
#transitions
even:a>odd
even:b>even
odd:a>even
odd:b>odd
FSM Design advice #
- Have a meaning for each state, its the only memory a FA has
- First write just the part that accepts good strings
- Make sure your FA is legal. Double check that every state has an arrow out for each alphabet symbol and that their’s a start state
- Try to break your solutions. Look for strings it accepts that it shouldn’t. Look for strings that it rejects that it shouldn’t.
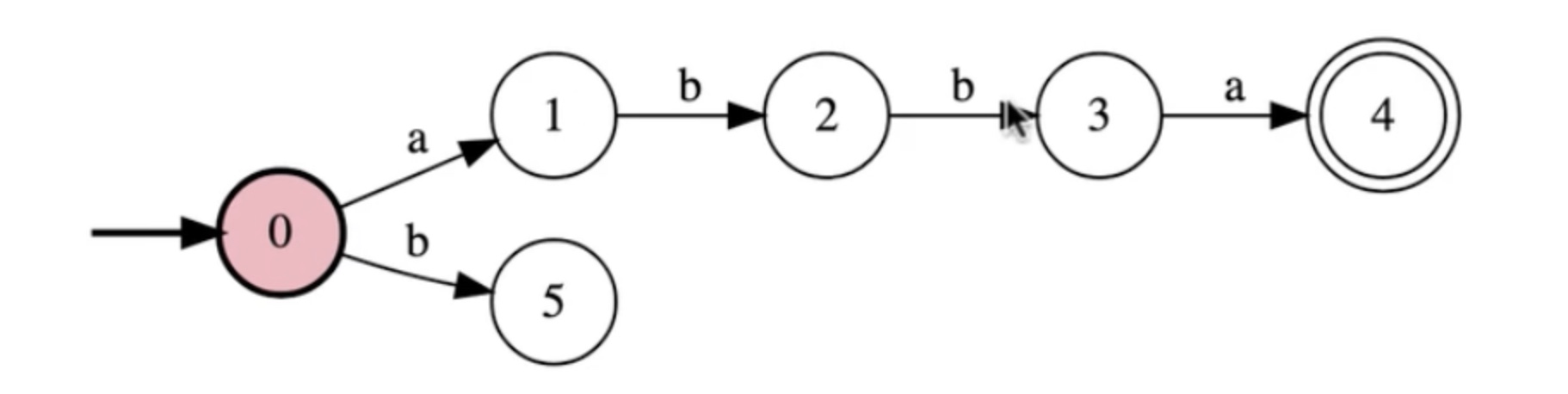
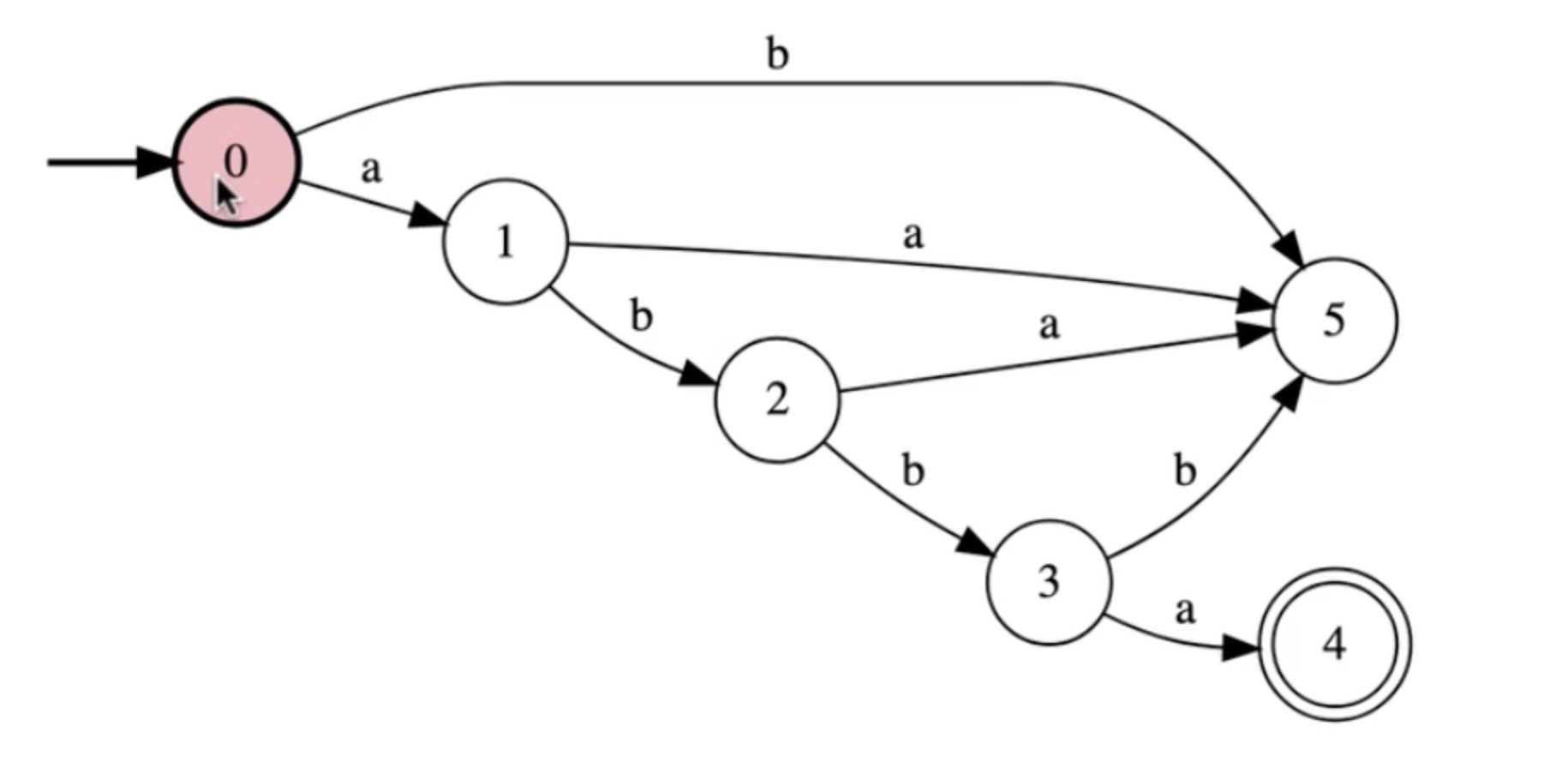
Write a FSM for the language: L = {abba}

This is the “write the part that accepts the good strings”.
We can start to figure out what we don’t want to initially accept in the string, “starting with a b”
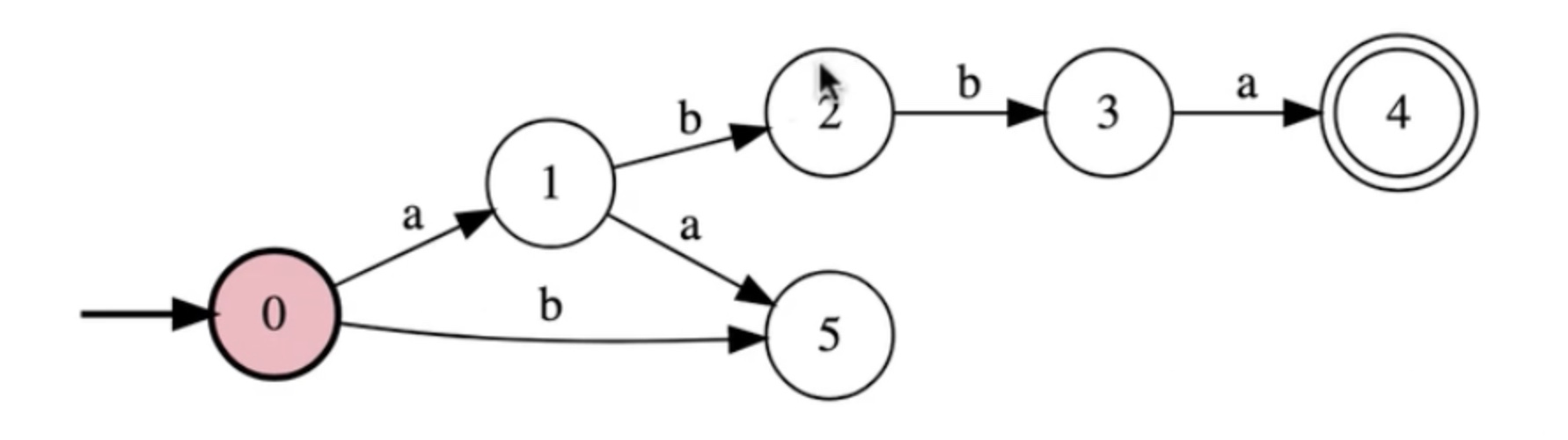
#alphabet
a
b
#states
0
1
2
3
4
5
#initial
0
#accepting
4
#transitions
0:a>1
0:b>5
1:b>2
1:a>5
2:b>3
2:a>5
3:a>4
3:b>5
4:a>5
4:b>5
5:a>5
5:b>5
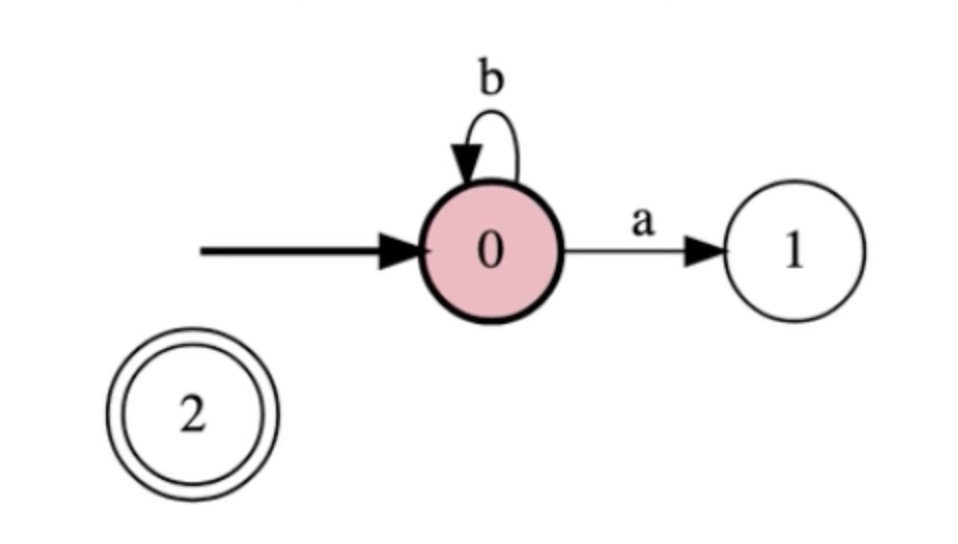
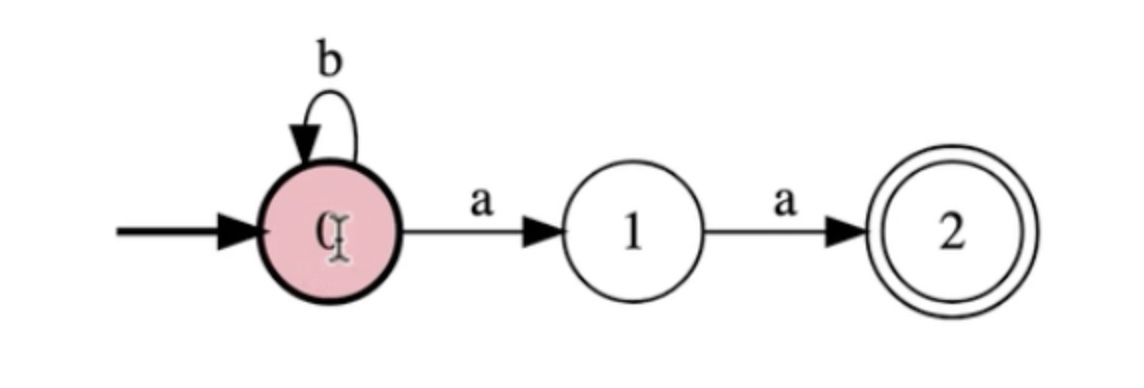
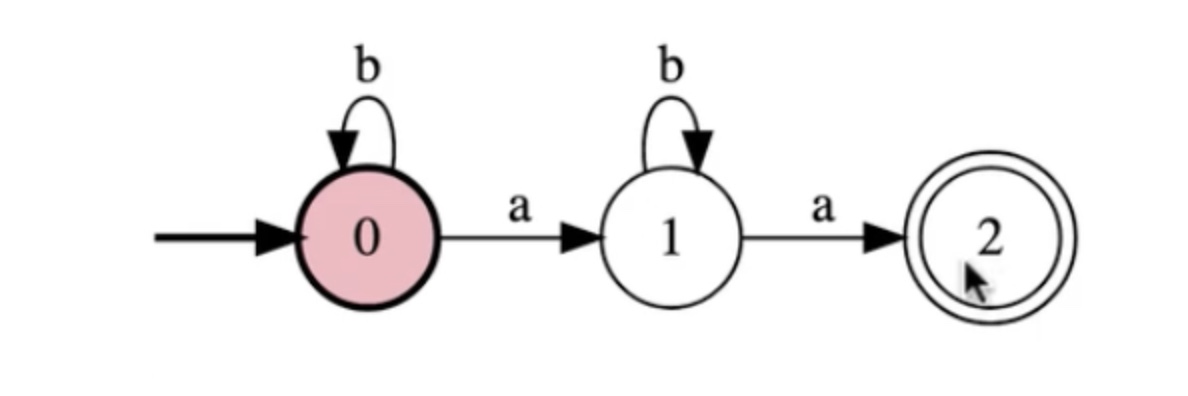
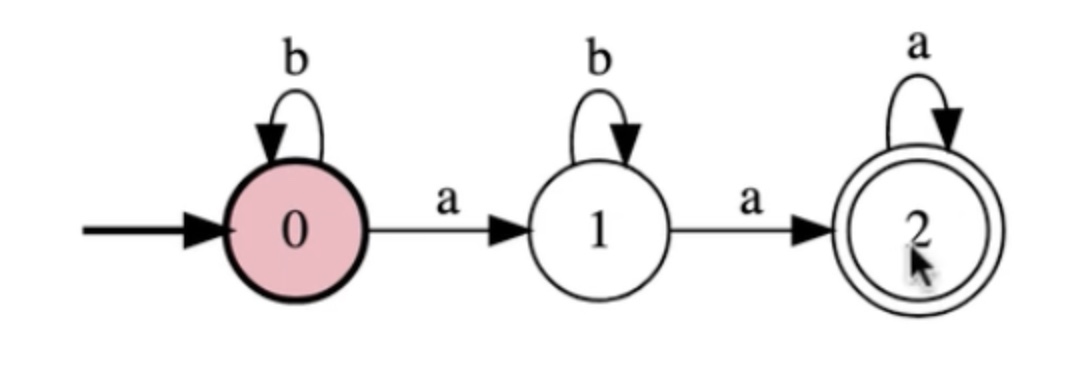
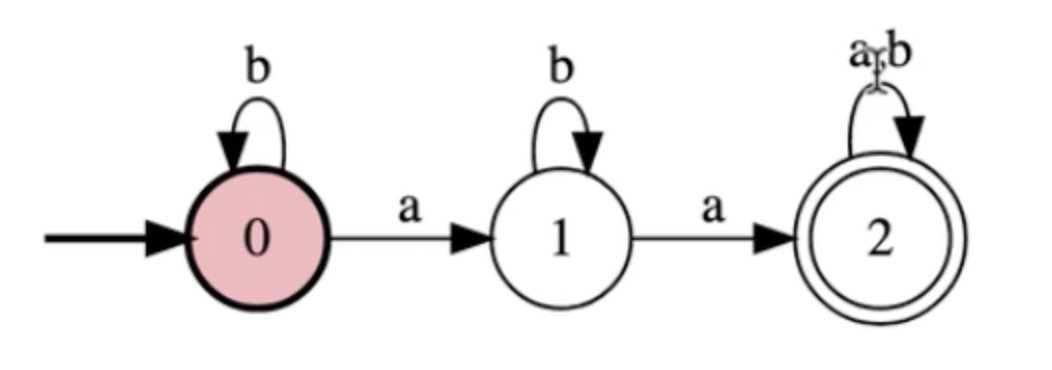
Write a FSM for the language {w in {a,b}*: w has at least two a's}
#alphabet
a
b
#states
0
1
2
#initial
0
#accepting
2
#transitions
0:a>1
0:b>0
1:a>2
1:b>1
2:a>2
2:b>2
In steps:
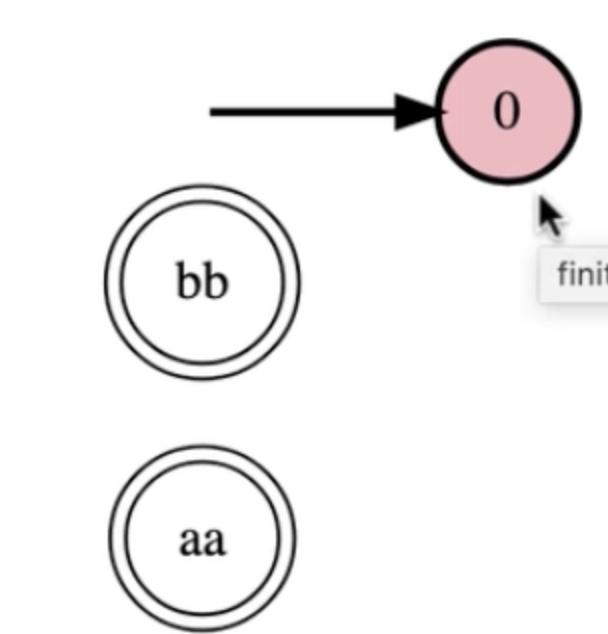
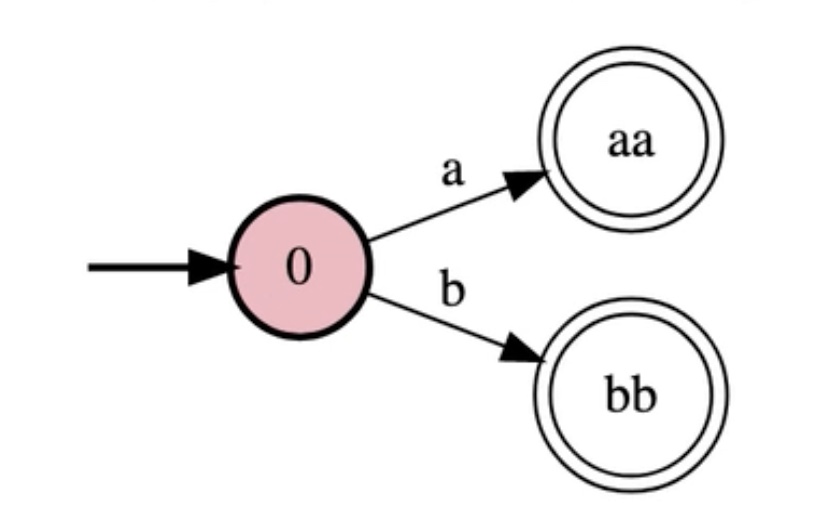
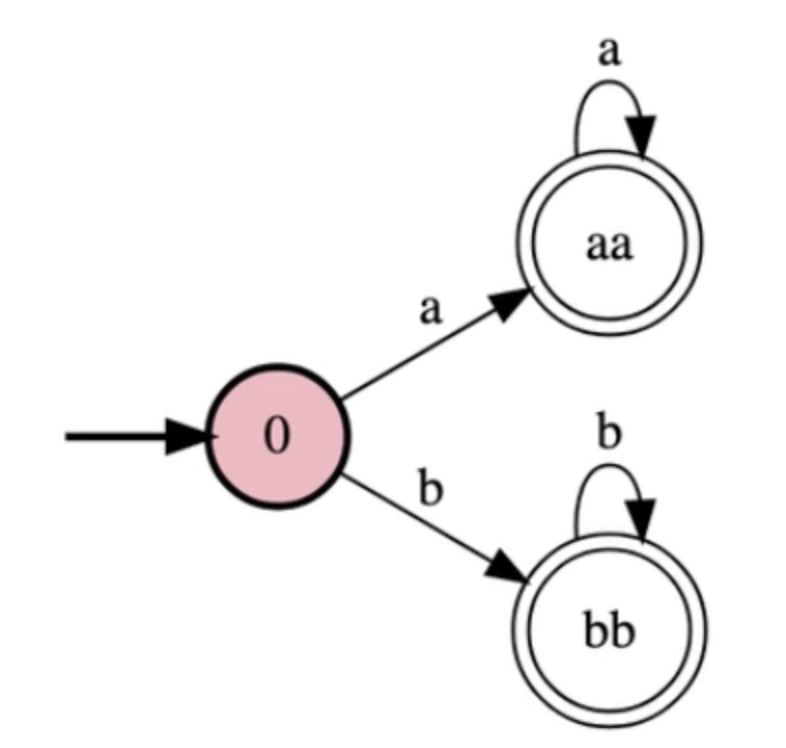
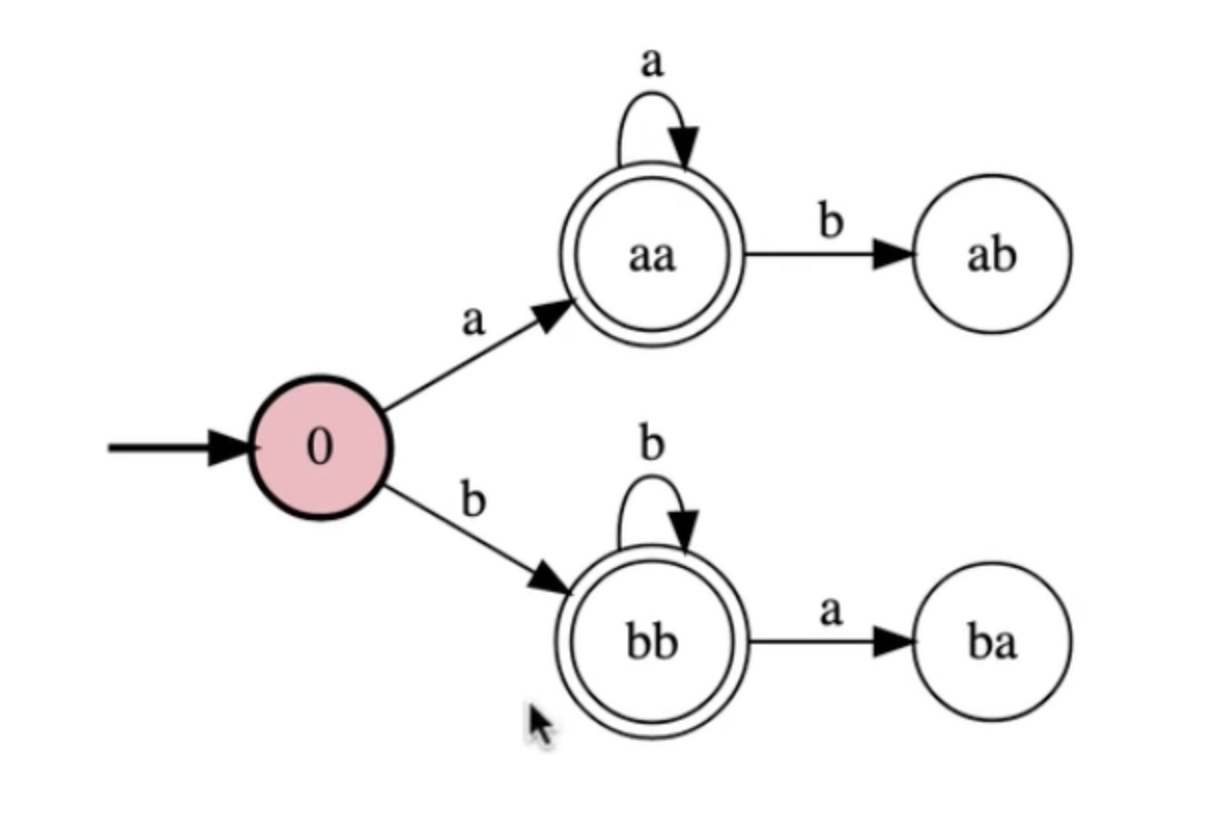
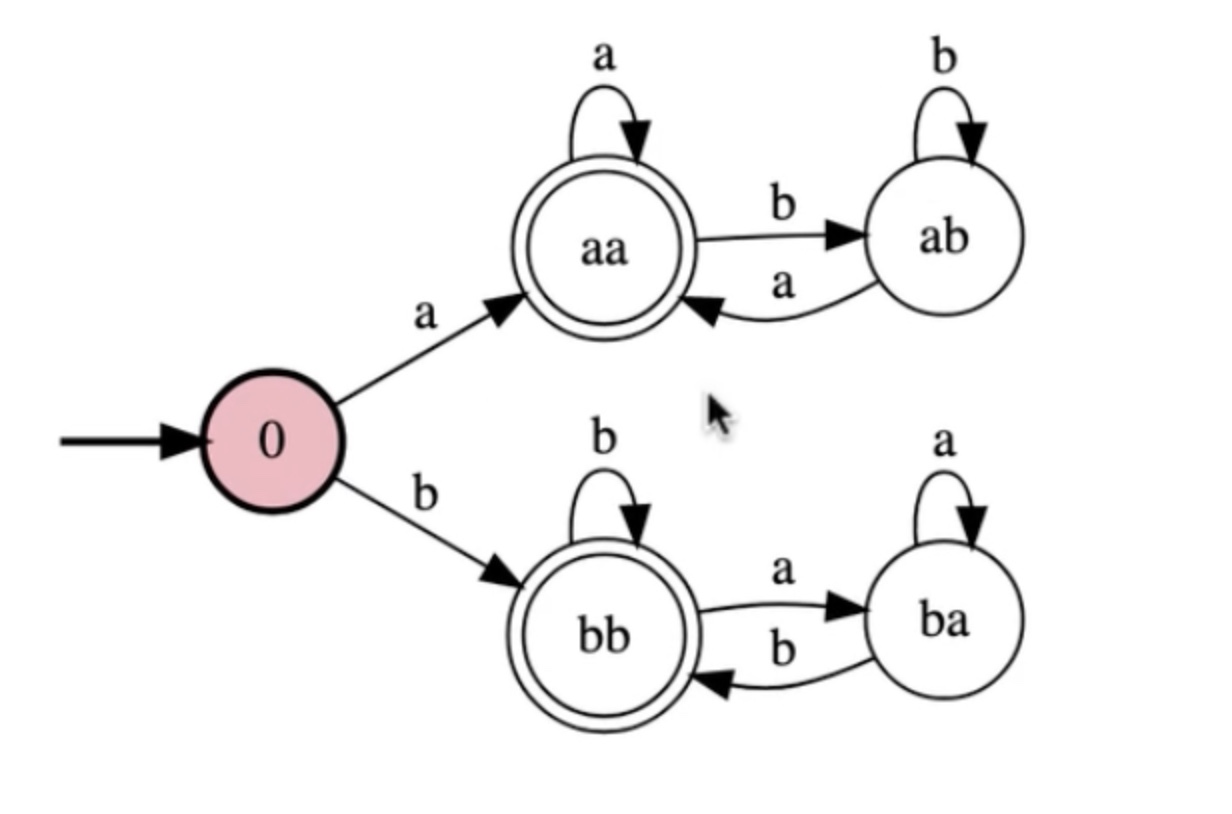
Write a FSM for the language {w in {a,b}* : w begins and ends in the same letter}
#alphabet
a
b
#states
0
aa
ab
ba
bb
#initial
0
#accepting
aa
bb
#transitions
0:a>aa
0:b>bb
aa:a>aa
aa:b>ab
bb:b>bb
bb:a>ba
ab:b>ab
ab:a>aa
ba:a>ba
ba:b>bb
In Steps:
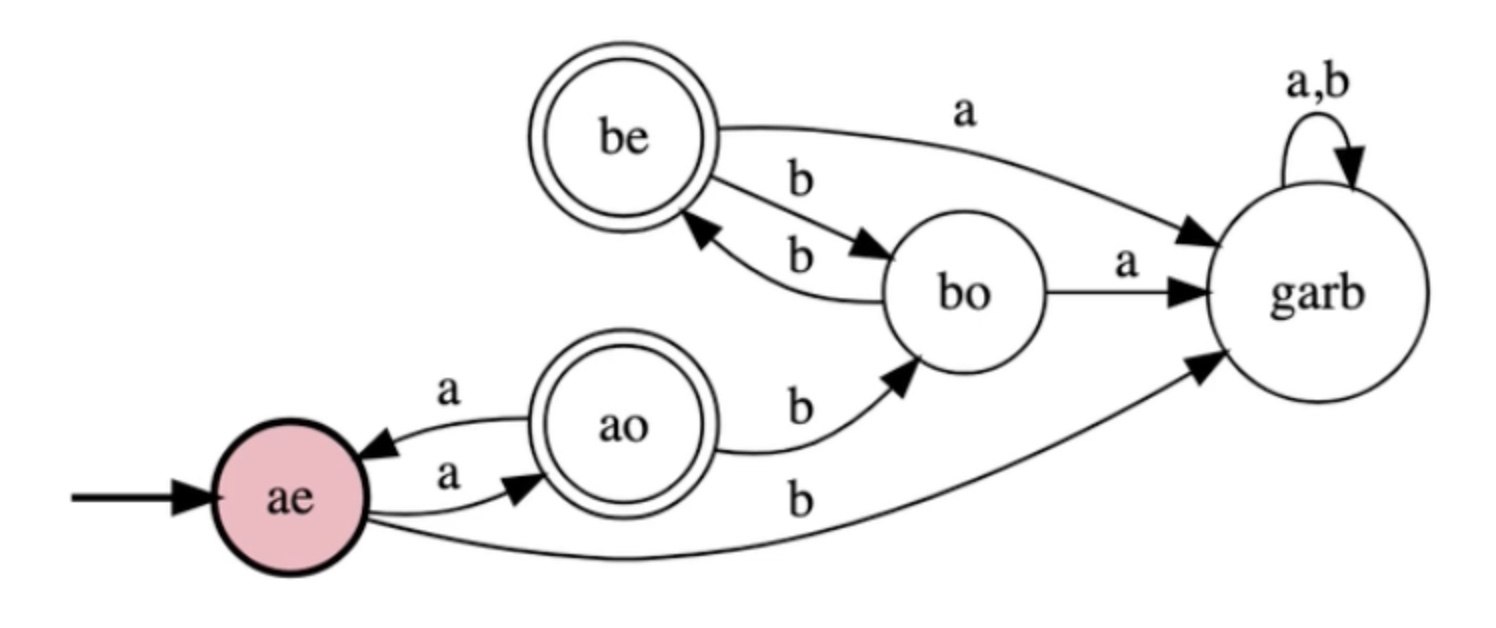
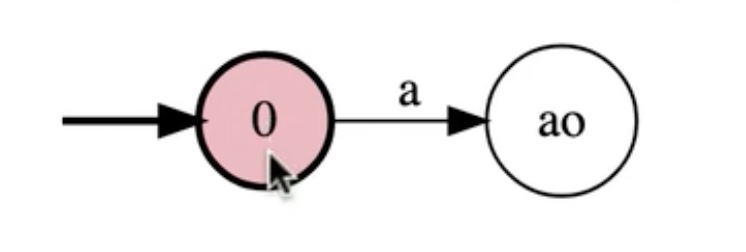
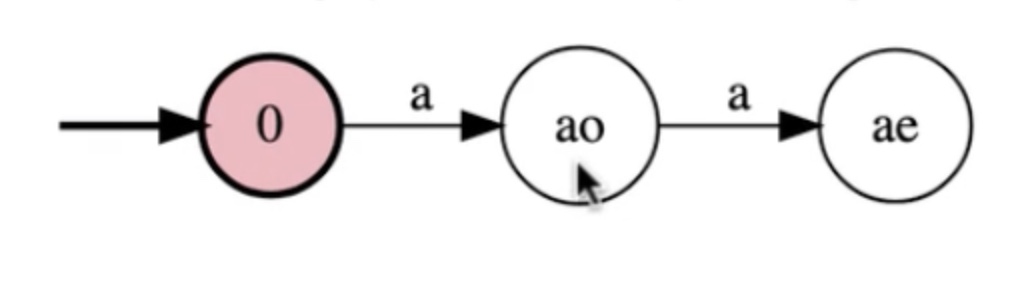
Write a FSM for the language: {a^n b^m : n is odd and m is even}
#alphabet
a
b
#states
0
ae
ao
be
bo
garb
#initial
0
#accepting
ao
be
#transitions
0:a>ao
0:b>garb
ao:a>ae
ae:a>ao
ae:b>garb
ao:b>bo
bo:b>be
be:b>bo
be:a>garb
bo:a>garb
garb:a>garb
garb:b>garb
In steps:
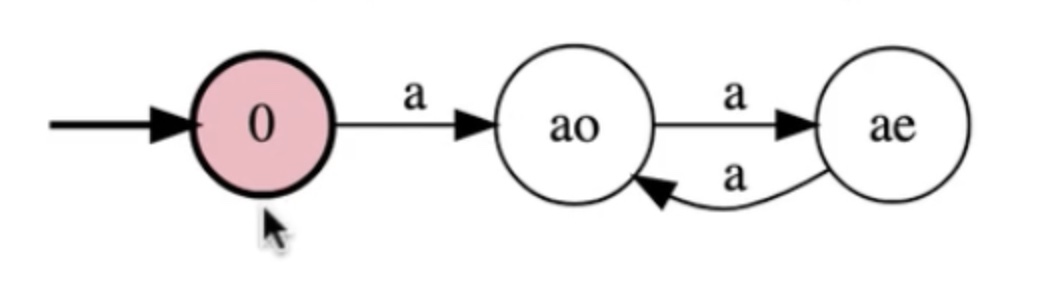
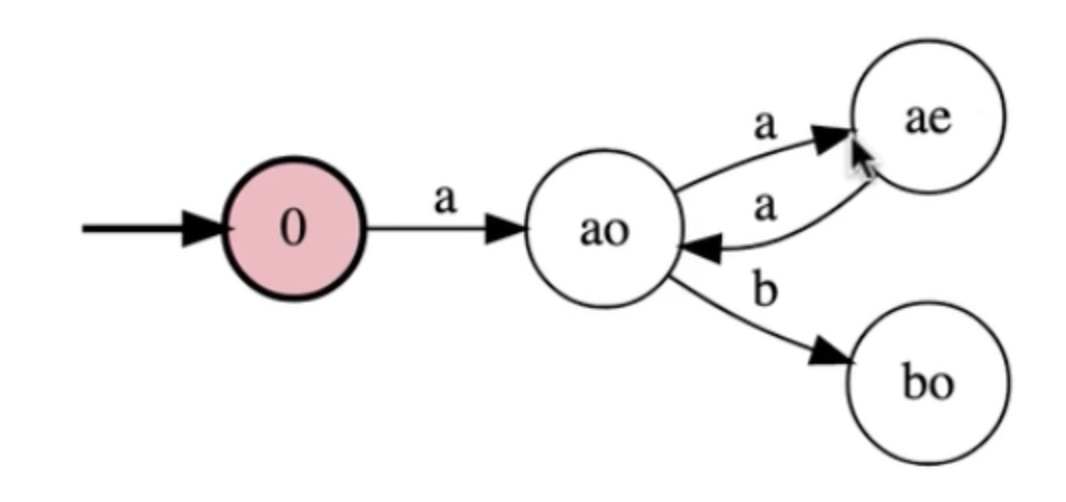
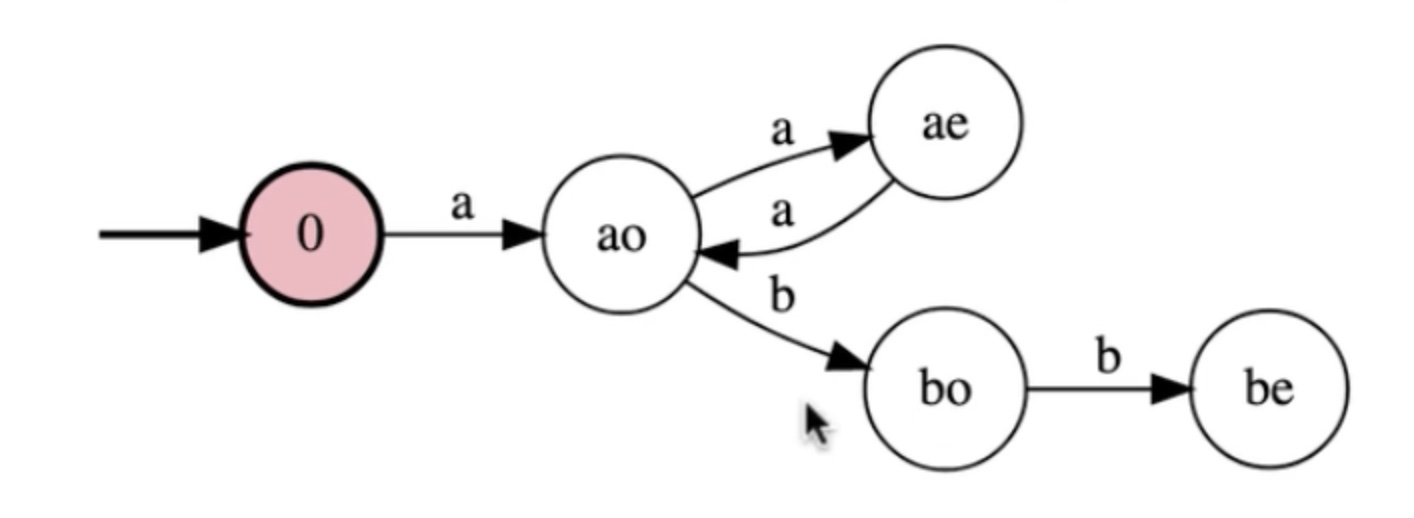
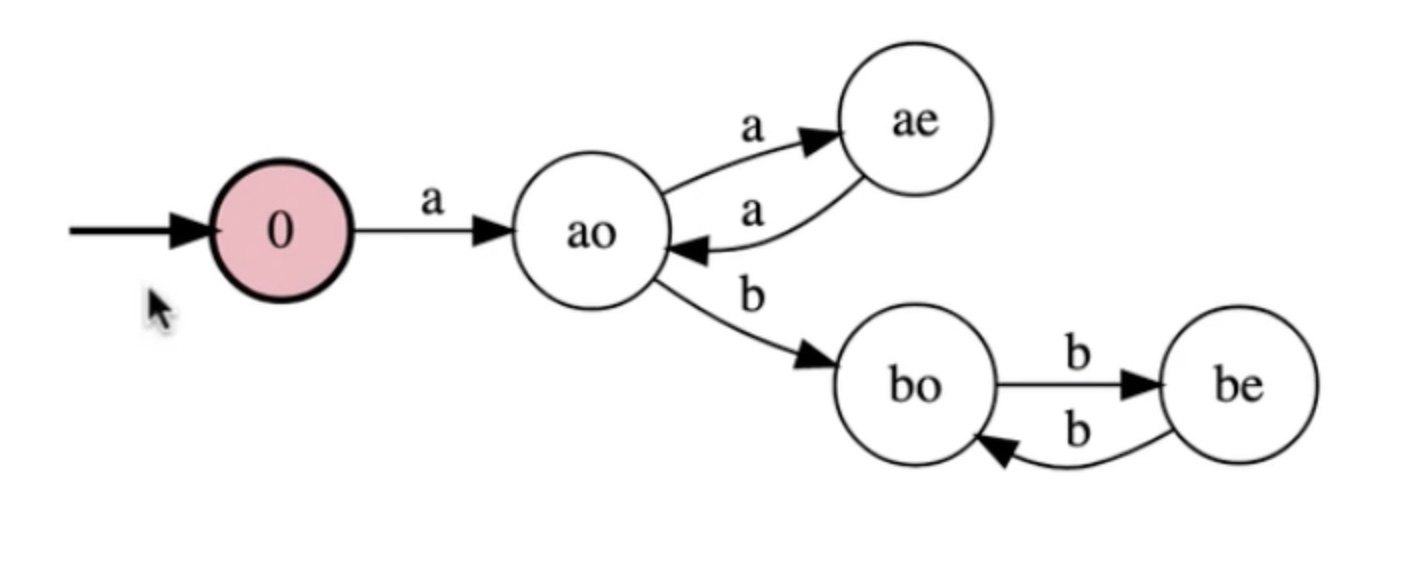
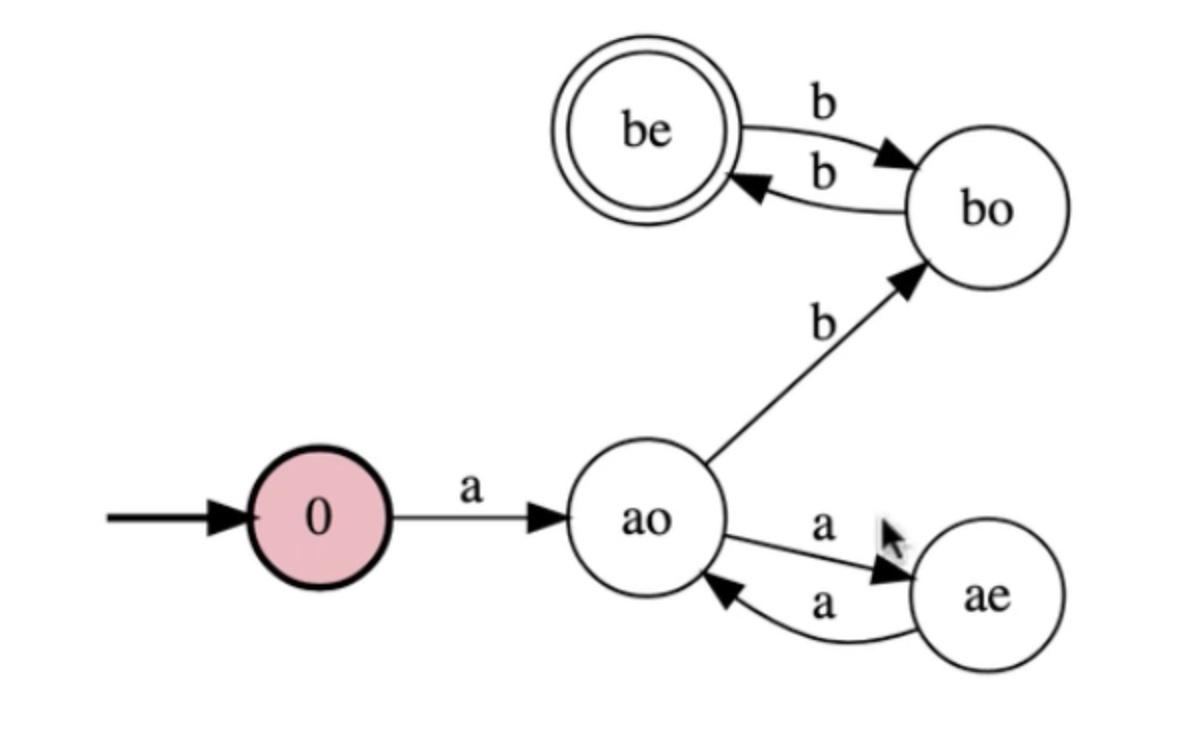
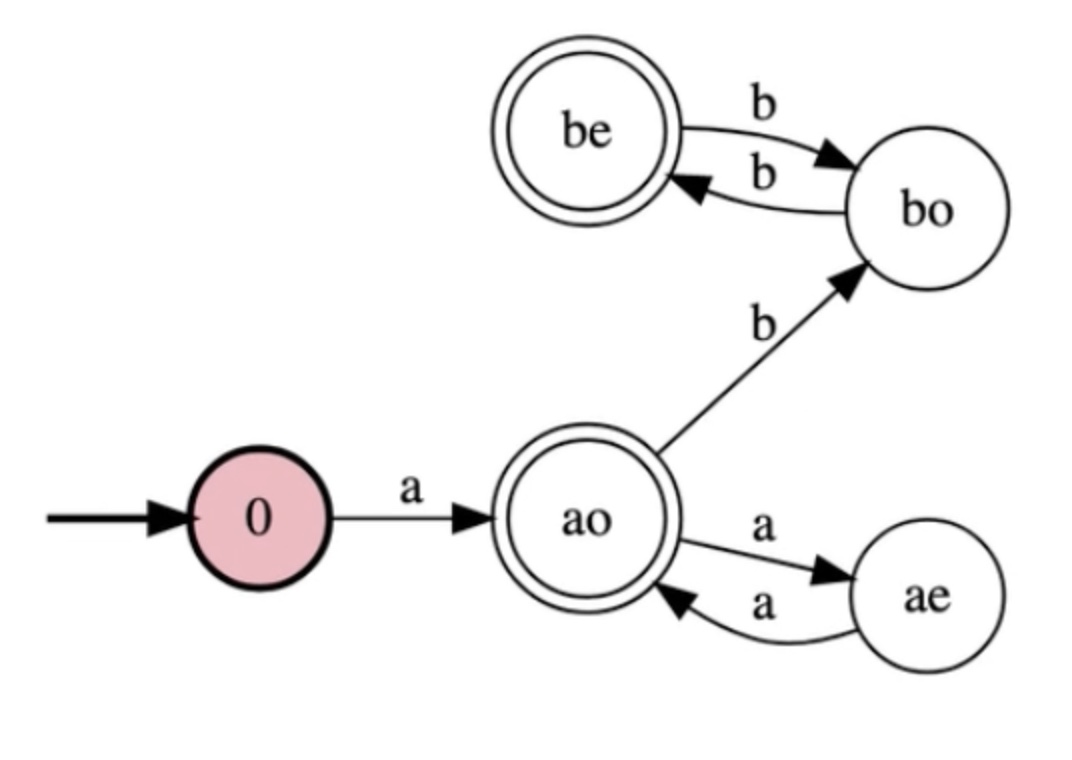
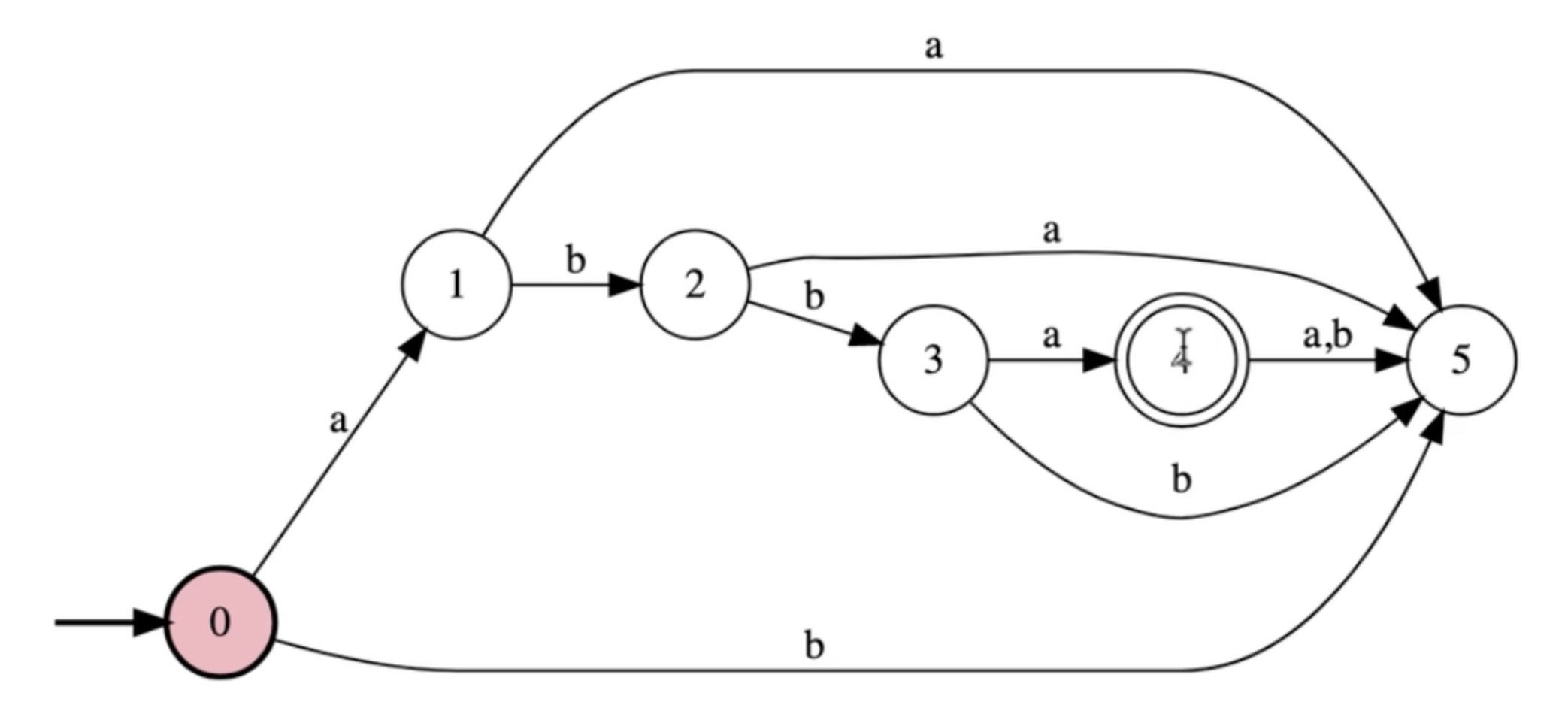
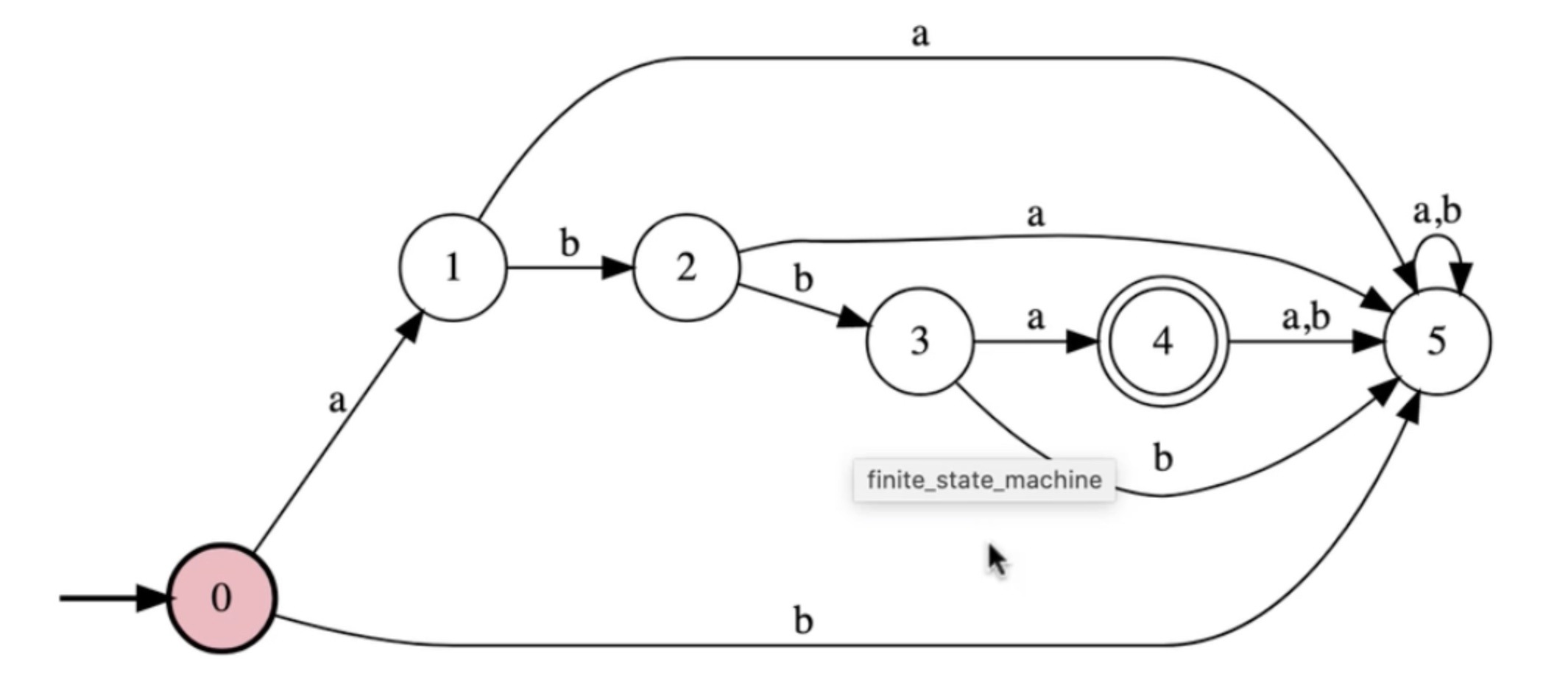
Now this accepts all the good strings, lets make it legal.
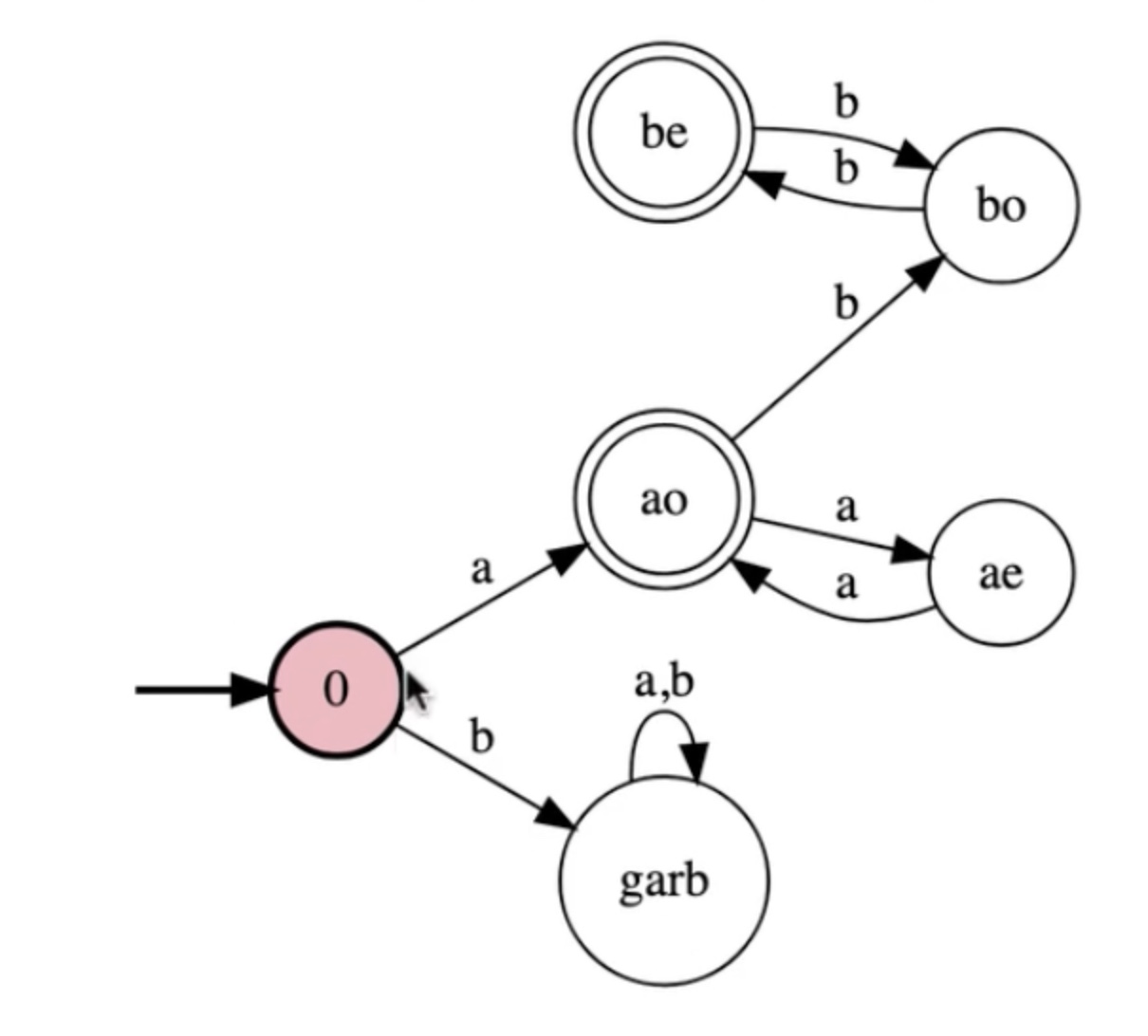
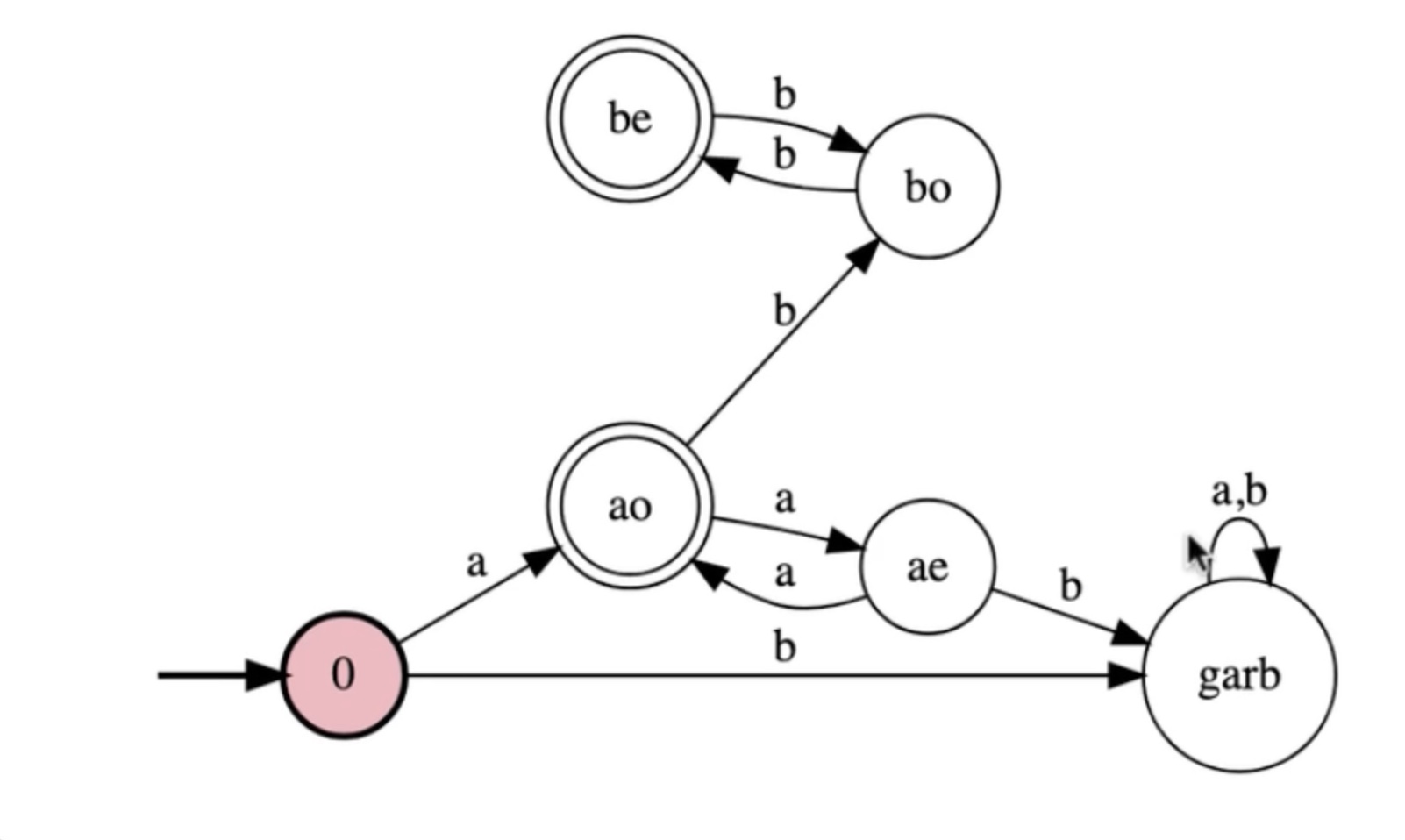
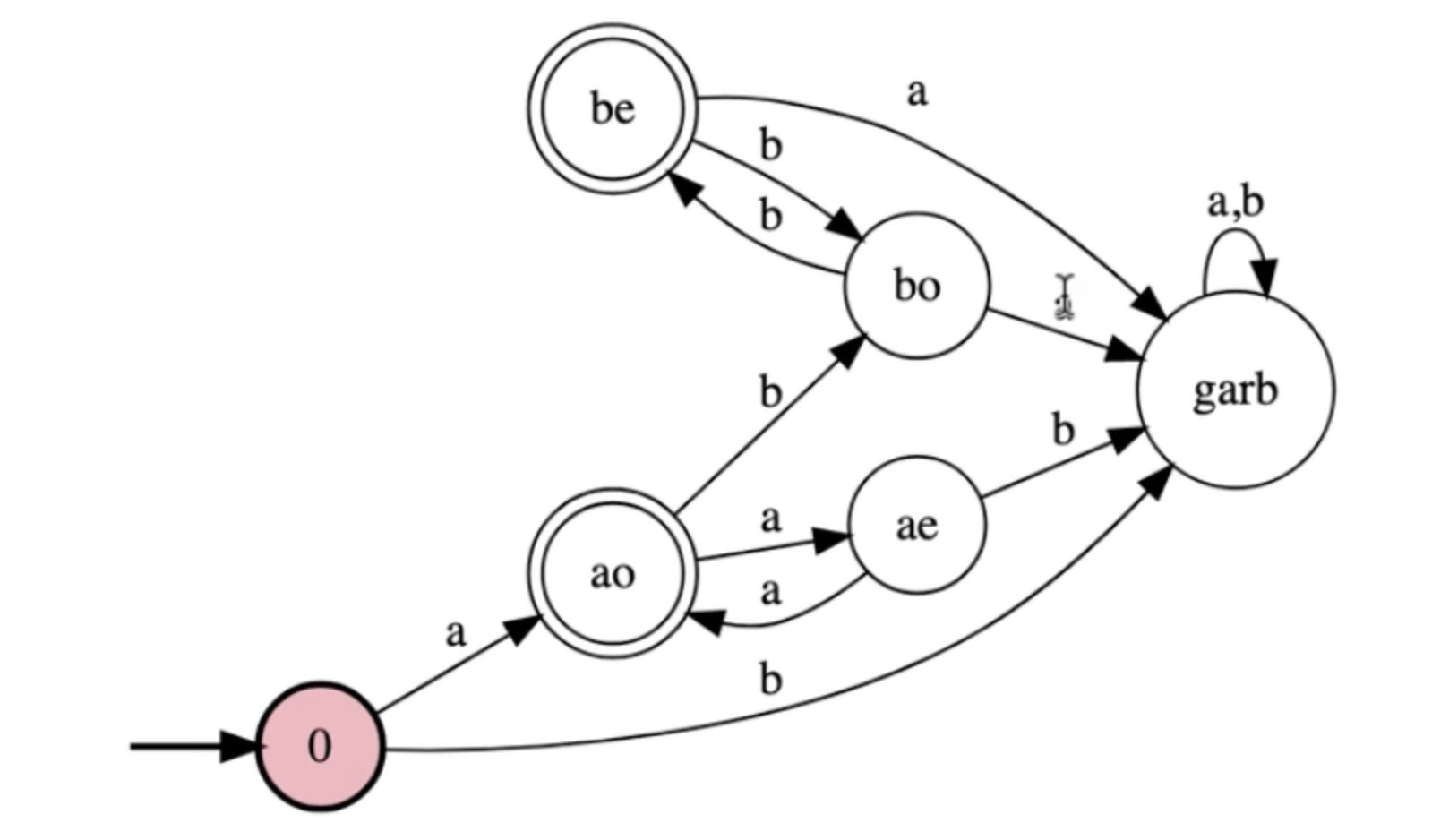
We can optimize this by making ae the initial state: