Normalization cont. #

We can also use an alternate notation to indicate dependencies:

If we remove the ssn then the dependency is no longer true.

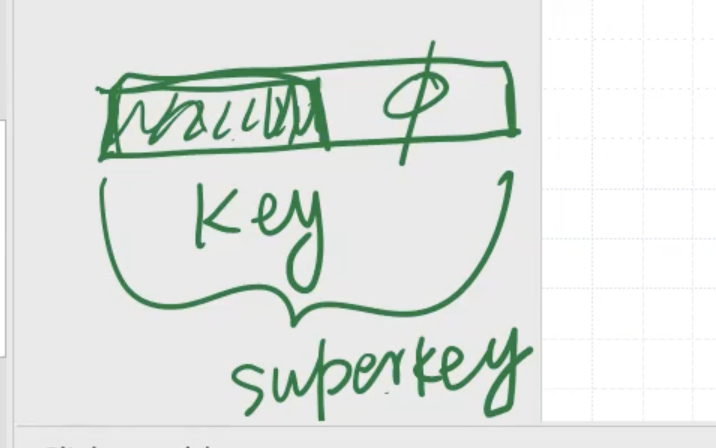
Second normal form #

An attribute that is part of any candidate key is a prime attribute. If we have a relation \[\begin{aligned} R(a, b, c, d, e) \end{aligned}\] and our candidate keys are \( \{a,b\} \) and \( c \) , that means our prime attributes are \( a,b,c \) .

Any attribute that isn’t a prime attribute is called an non-prime attribute, that is it is not part of any candidate key. So our non-prime attributes from the last example are \( d,e \) .

A relational schema \( R \) is in second normal form if every non-prime attribute \( A \) in \( R \) is fully functionally dependent on every key of \( R \) .

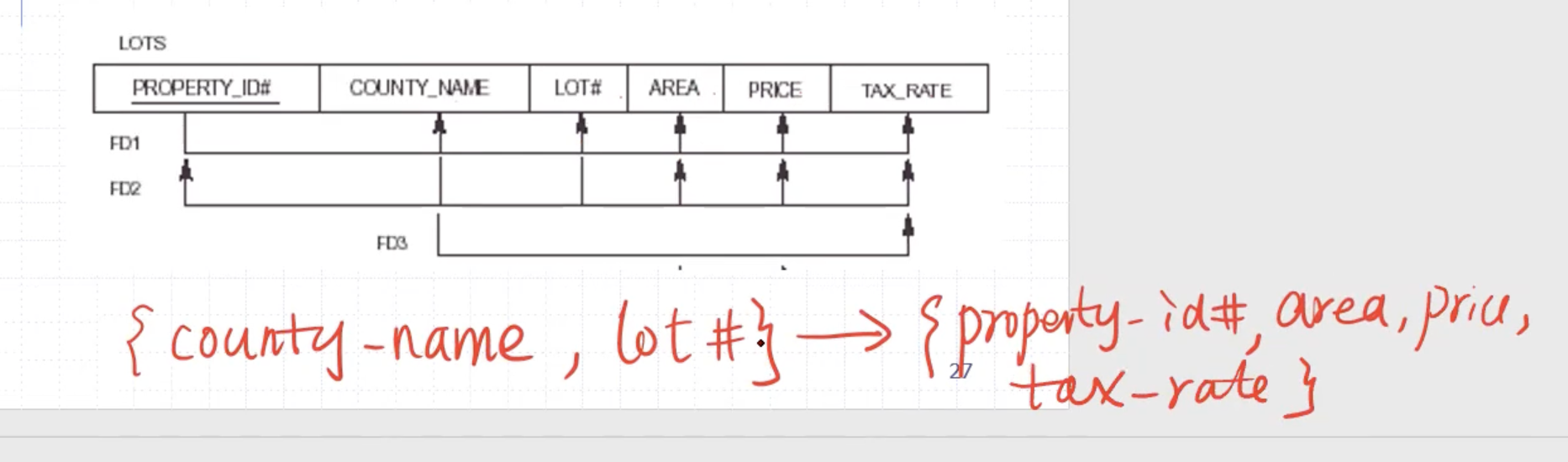
• FD1. if we know the PROPERTY_ID then we also know the attributes COUNTY_NAME, LOT#, AREA, PRICE, TAX_RATE
• FD2. if we know the COUNTY_NAME and LOT#, then we also know the attributes PROPERTY_ID AREA PRICE TAX_RATE
• FD3. if we know the COUNTY_NAME, then we also know the TAX_RATE

So is this in second normal form?

• Our non-prime attributes are AREA PRICE and TAX_RATE, we need to go through and make sure each of these non-prime attributes are fully functional on the keys.
  • Is AREA fully functionally dependent on PROPERTY_ID? \[ \begin{aligned} \text{property id} \to \text{area} \end{aligned} \] Yes, because we cannot remove anything from the left hand side and have the dependency hold true. (Any attribute that depends on a single key will automatically be fully functionally dependent).
  • The rest of the non-prime attributes are fully functionally dependent on PROPERTY_ID for the same reason as above
  • Next we need to check if the non-primes are fully functionally dependent on the key {COUNTY_NAME, LOT#} \[ \begin{aligned} \{ \text{county name, lot num} \} \to \text{area} \end{aligned} \] If we remove LOT# will this dependency still hold true? Yes, this is fully functionally dependent. (If there was another dependency COUNTY_NAME \( \to \) AREA then it would still hold true). \[ \begin{aligned} \{ \text{county name, lot num} \} \to \text{price} \end{aligned} \] This is also fully functionally dependent for the same reason. \[ \begin{aligned} \{ \text{county name, lot num} \} \to \text{tax rate} \end{aligned} \] This is not fully functionally dependent because if we remove LOT#, there still exists a dependency COUNTY_NAME \( \to \) TAX_RATE (FD3).
• Therefore, this is not in second normal form because non-prime attribute TAX_RATE is not fully functionally dependent on key {COUNTY_NAME, LOT#}.

Note: As soon as you find a single non-prime attribute that is not fully functionally dependent on a key you can immediately see it is not in second normal form.

In class exercise #

Include this in weekly homework.

Consider the relation

where the keys are \( \{A,B\}, \{C,D\} \) , and the dependencies are

Is \( R \) in second normal form?

• The non-prime attribute is \( E \) . So is \( E \) fully functional on all keys?
  • Is \( E \) fully functionally dependent on \( \{A,B\} \) ? Yes.
  • Is \( E \) fully functionally dependent on \( \{C,D\} \) ? Yes.
• Therefore, \( R \) is in second normal form.

Include this in weekly homework.

Consider the relation \[\begin{aligned} R(A, B, C, D) \end{aligned}\] with key \( \{A,B\} \)

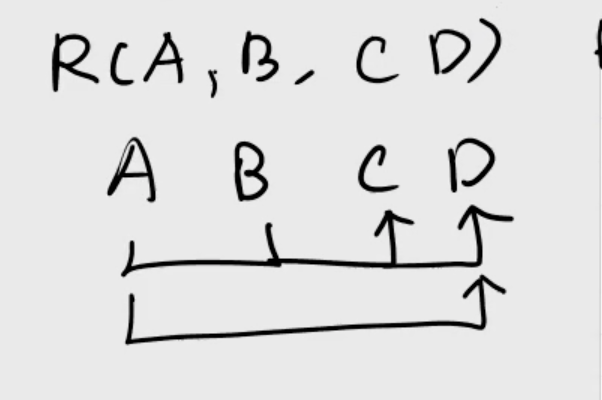
Is \( R \) in second normal form?

No, because we can remove \( B \) from the dependency \[\begin{aligned} \{A,B\} \to D \end{aligned}\] and still fulfill the depdendency via \[\begin{aligned} A \to B \end{aligned}\]

So, \( R \) is not in second normal form.

Third normal form #

Third normal form is easier to check than second normal form.

A relational schema \( R \) is in third normal form if, whenever a non-trivial functional dependency \( X \to A \) holds in \( R \) , then either

• \( X \) is a superkey of \( R \) , or
• \( A \) is a prime attribute of \( R \)

Recall, any key is a superkey:

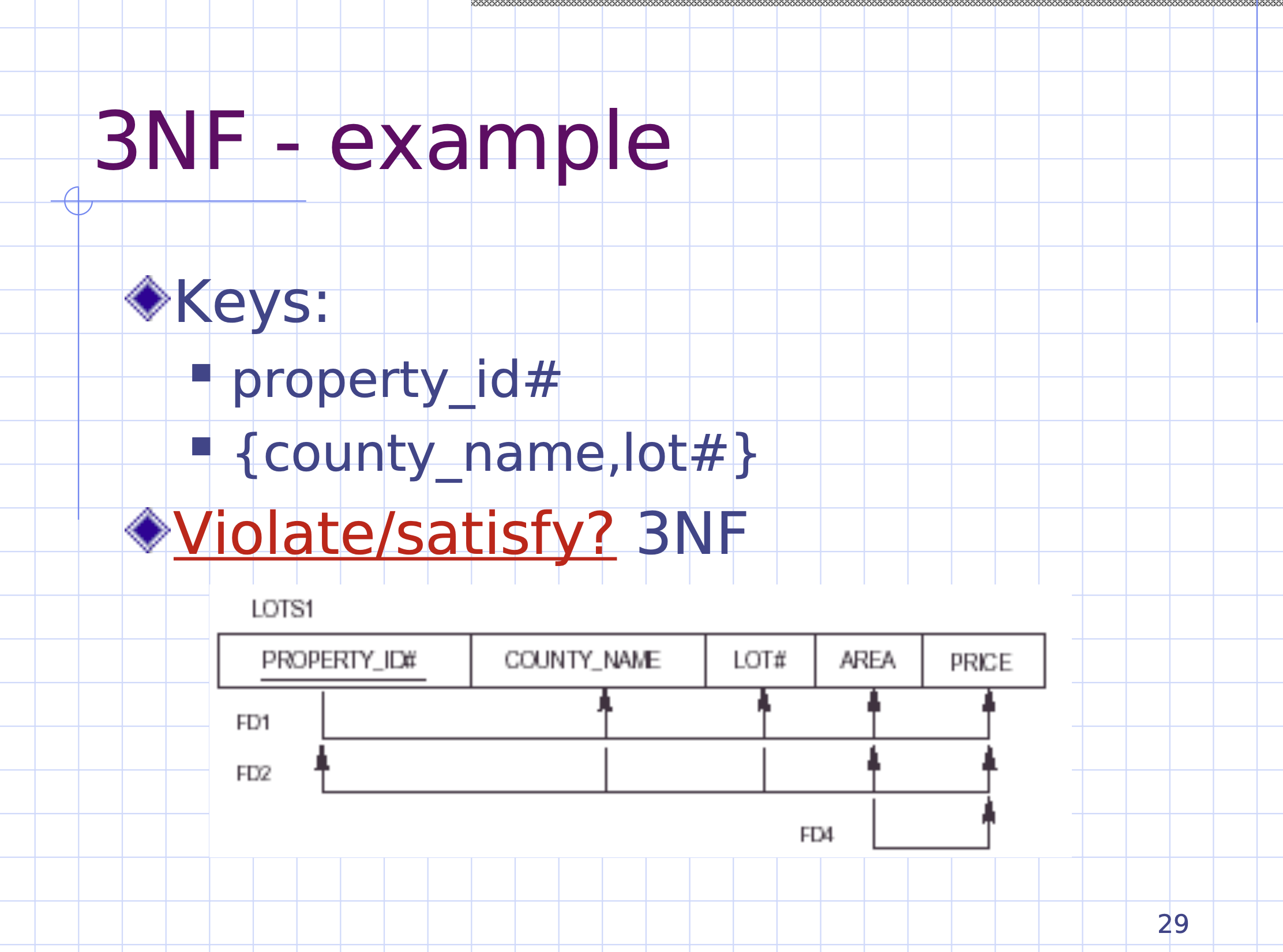
So is this schema in third normal form?

• First we should check to see if FD1 has any violation
  • Check left hand set {PROPERTY_ID}: Is this a superkey? Yes.
• Check if FD2 has any violation
  • Check left hand set {COUNTY_NAME, LOT#}: Is this a superkey? Yes.
• Check if FD4 has any violation
  • Check left hand set {AREA}: Is this a superkey? No.
  • Check right hand set {PRICE}: Is this a prime attribute? No.
• Therefore, since we had a violation, this schema is not in third normal form.

In class exercise #

Include in weekly homework.

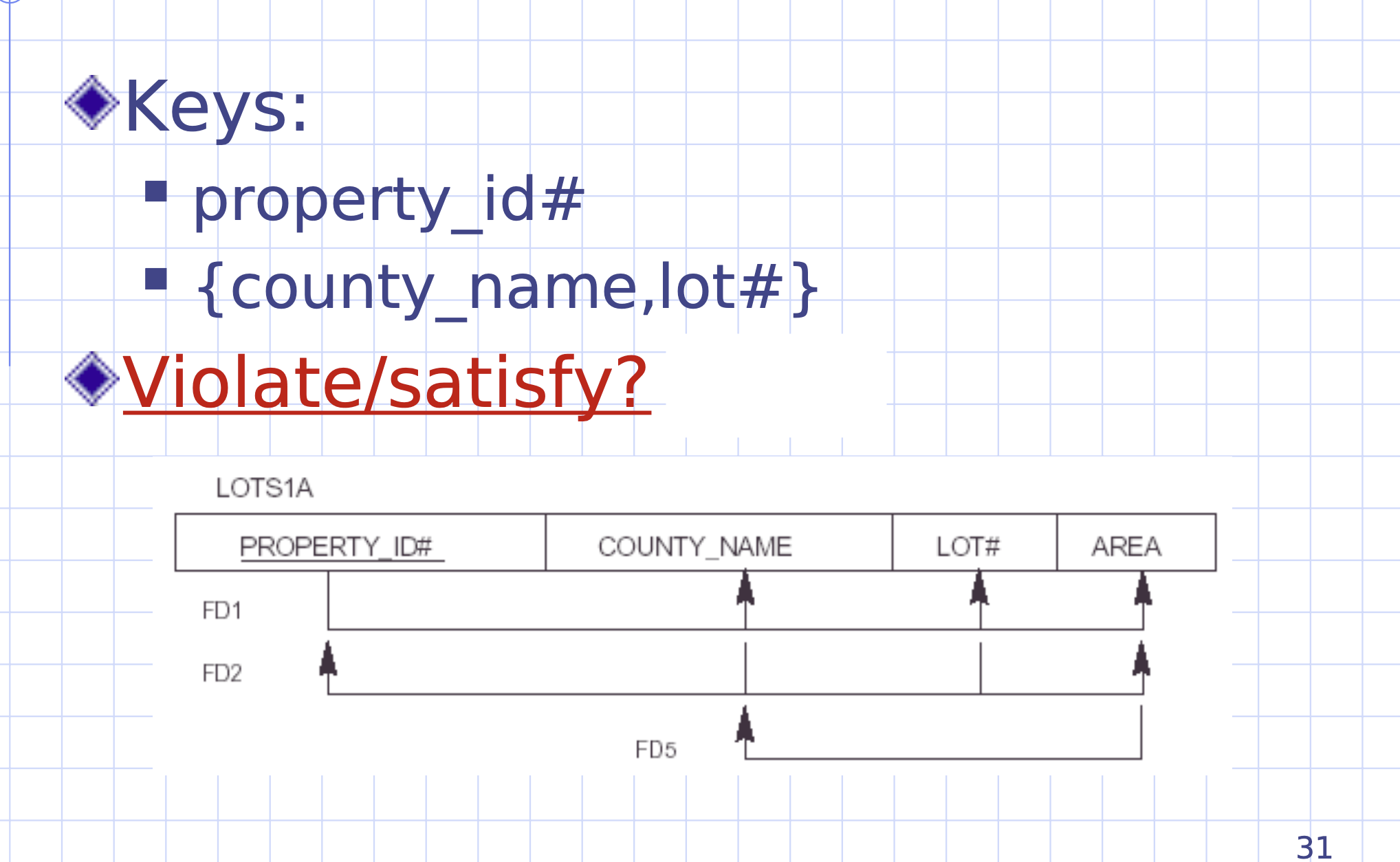
Is this schema in third normal form?

• Check FD1
  • Left hand set is a superkey, good.
• Check FD2
  • Left hand set is a superkey, good.
• Check FD5
  • Left hand set is not a superkey…
  • Right hand set is a prime attribute, good.
• Therefore, this schema is in third normal form.

Boyce-Codd normal form (BCNF) #

This is the highest normal form we will study.

A relational schema \( R \) is in Boyce-Codd Normal Form (BCNF) if whenever a nontrivial functional dependency \( X \to A \) holds in \( R \) , then \( X \) is a superkey of \( R \) .

This is a stricter version of the third normal form, it only checks the first condition.

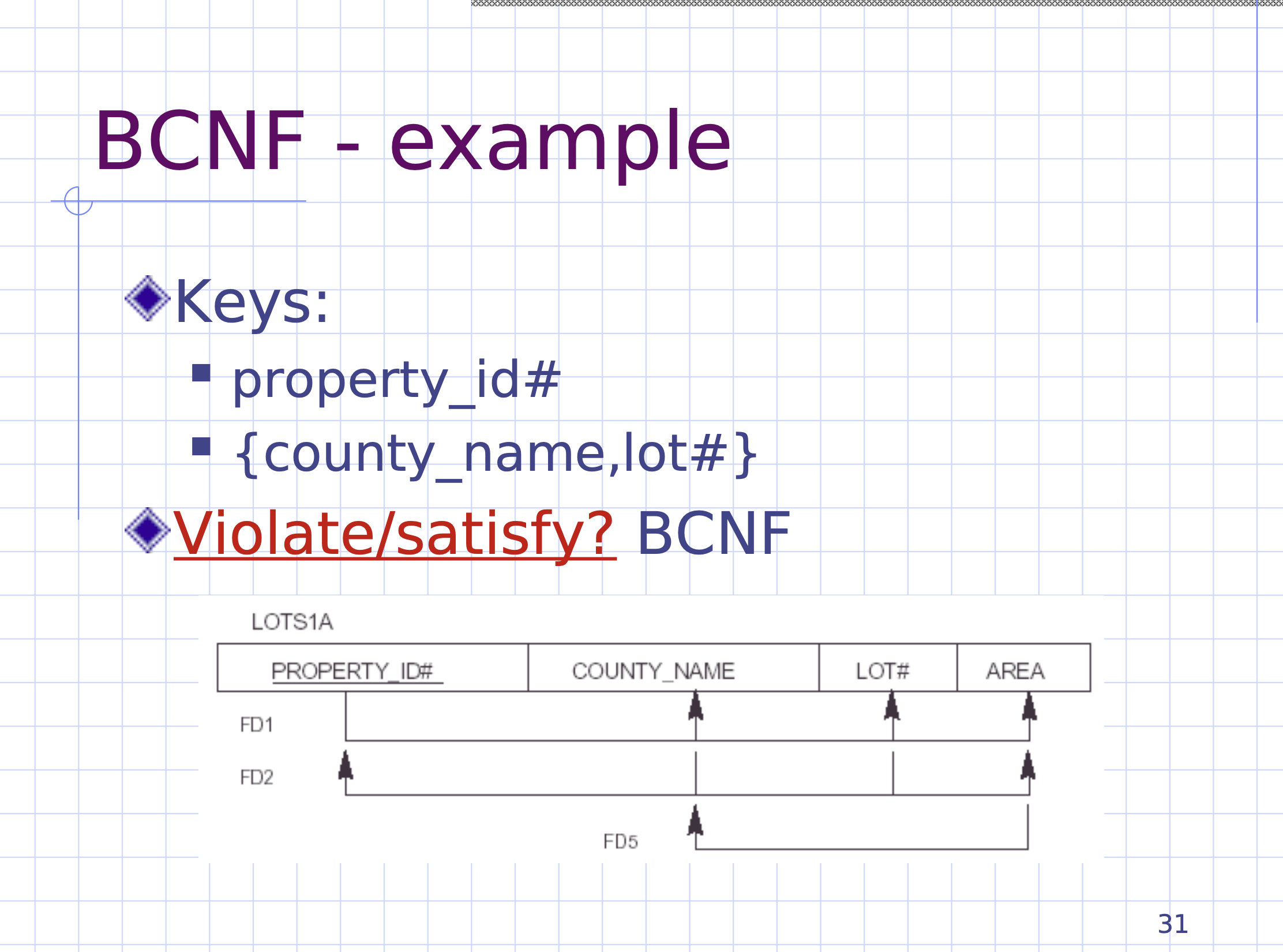
Is this schema in BCNF?

• Check FD1
  • Left hand set is a superkey, good.
• Check FD2
  • Left hand set is a superkey, good.
• Check FD5
  • Left hand set is not a superkey.
• Therefore, this schema is not in BCNF.

Normal form examples #

If we have the relation \[\begin{aligned} R(A, B, C, D, E) \end{aligned}\] with key \( \{A,B\} \) , and we have these dependencies:

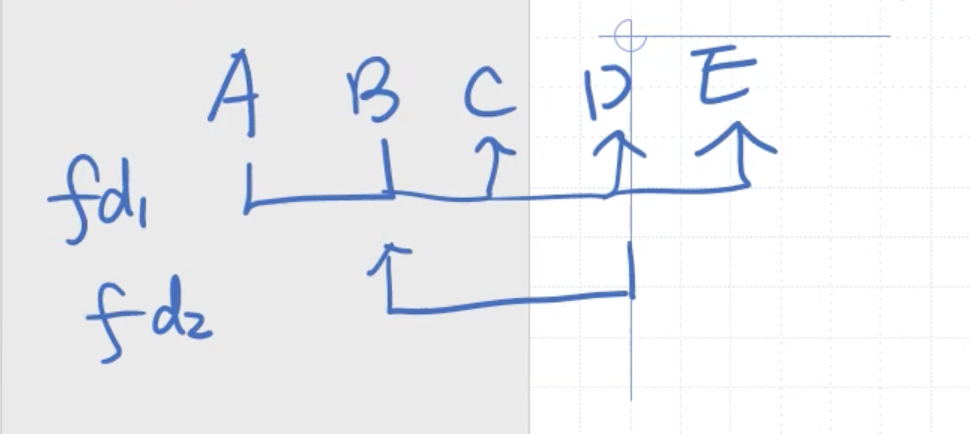
Which normal form is \( R \) in? Why?

1. Is \( R \) in BCNF?
   • FD1: left hand set is a superkey? Yes
   • FD2: left hand set is a superkey? No
   • Not in BCNF
2. Is \( R \) in third normal form?
   • FD1: left hand set is a superkey? Yes
   • FD2: left hand set is a superkey? No. Right hand set prime attribute? Yes
   • Passed third normal form checks

Therefore, \( R \) is in third normal form.

Note: We can check normal forms in increasing or decreasing order.

Storage #

File: Storage slides

Now that we’ve finished studying implementation, we will look at physical storage. We will look closer at how a DBMS accesses files on disk.

Specific file format meant for read/write by the DBMS.

Physical storage #

Records #

Record spanning #

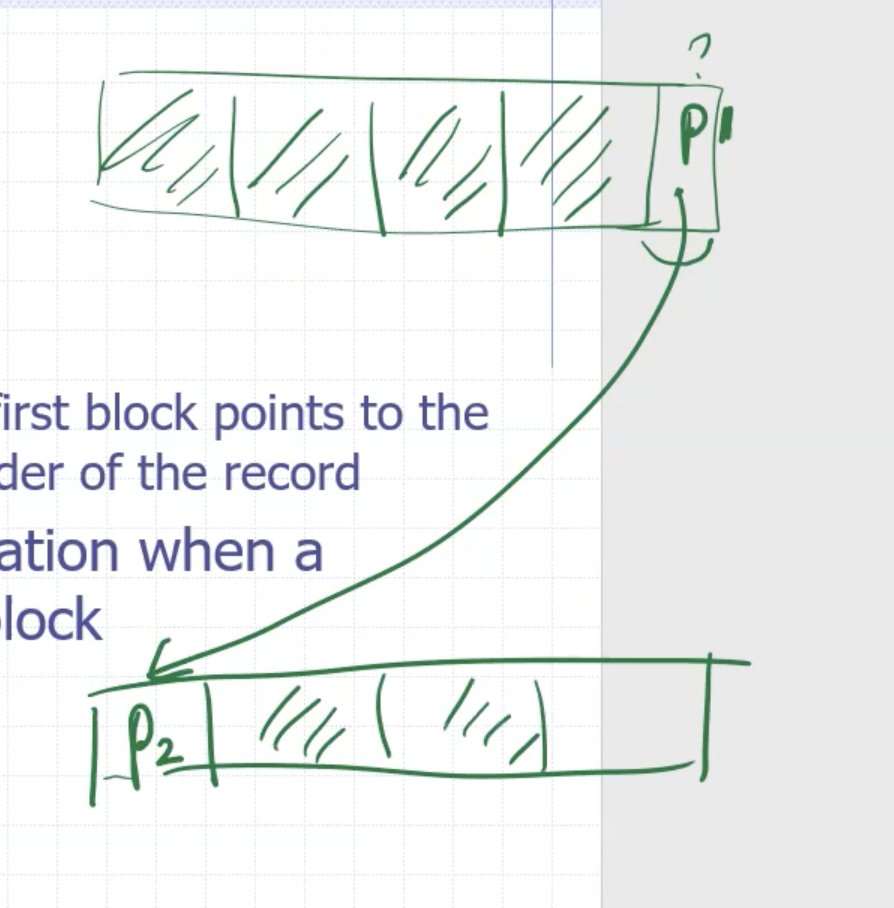
File headers #

File operations #

Record ordering #

Moving items when deleting from the middle, ie

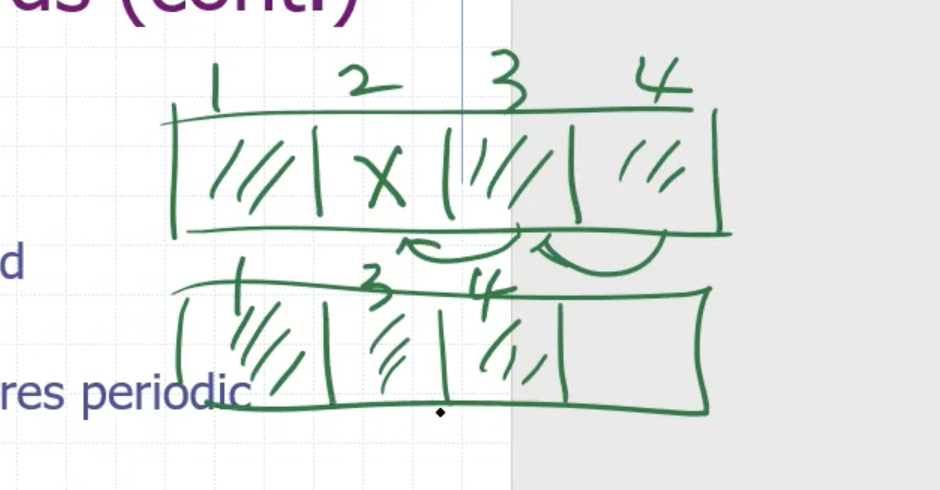
can be really expensive. So instead we put a marker for deletion in place

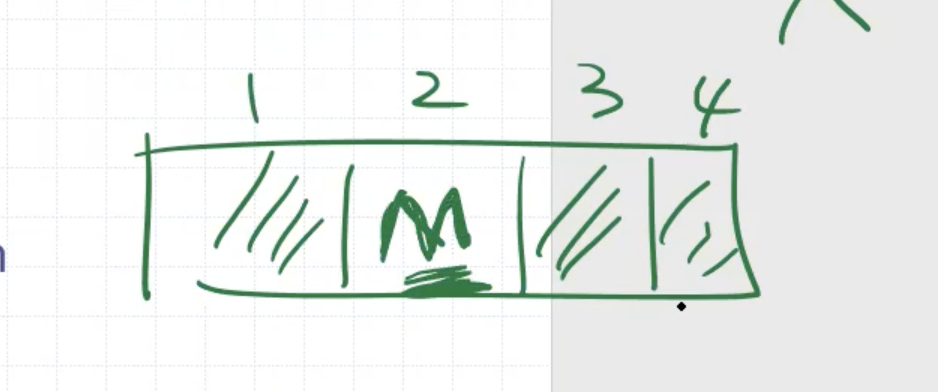
Once there are a lot of markers in a block, space will have to be reorganized.

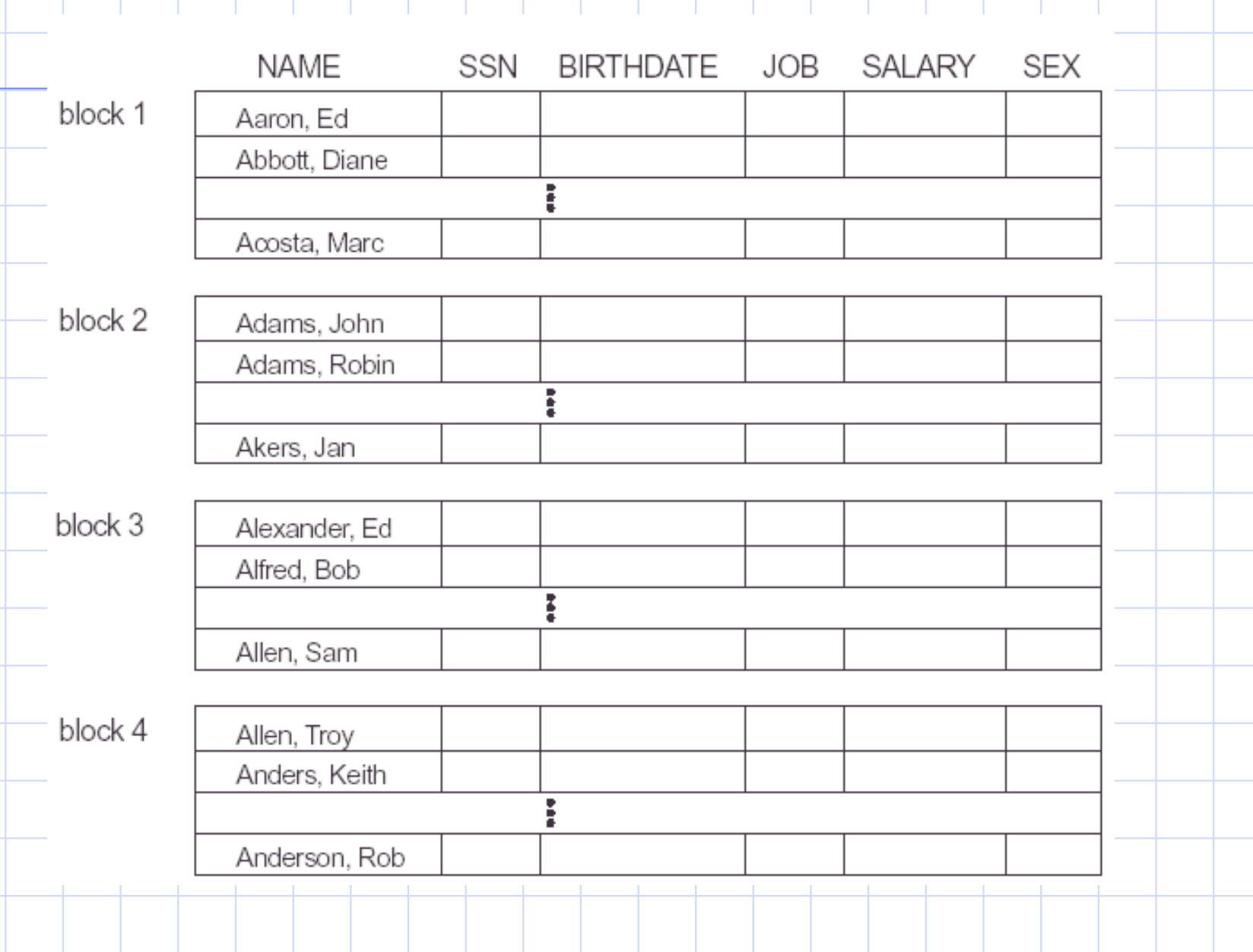
• This file spans multiple blocks
• It is sorted by name
• If we search based by name, we can use binary search, resulting in \( O(\lg n) \) time complexity.
• If we search by salary, best we can do is a linear search, resulting in \( O(n) \) time complexity.
  • If we order by salary, then we could use a binary search.