CS134-lecture-20210616

Relational algebra cont. #

Natural join cont #

image_2021-06-16-15-51-53

\begin{aligned} \text{dept locs} \leftarrow \text{department} * \text{locations} \end{aligned}

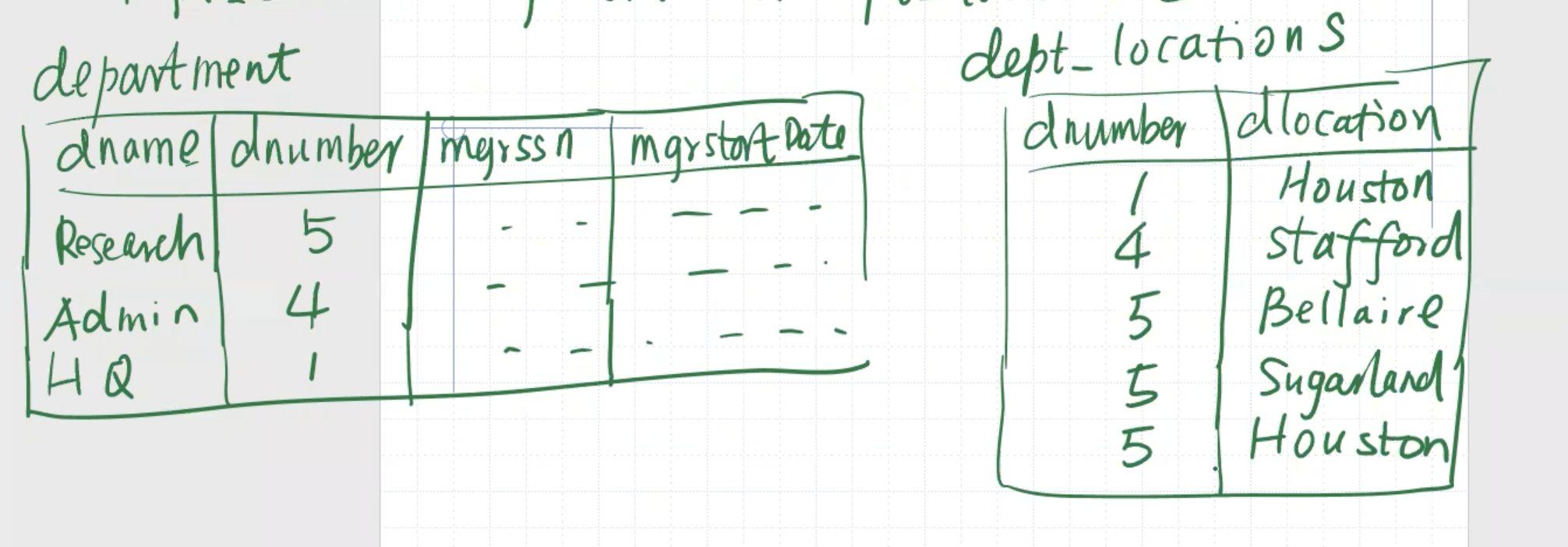
image_2021-06-16-15-54-39

Our natural join results in this table

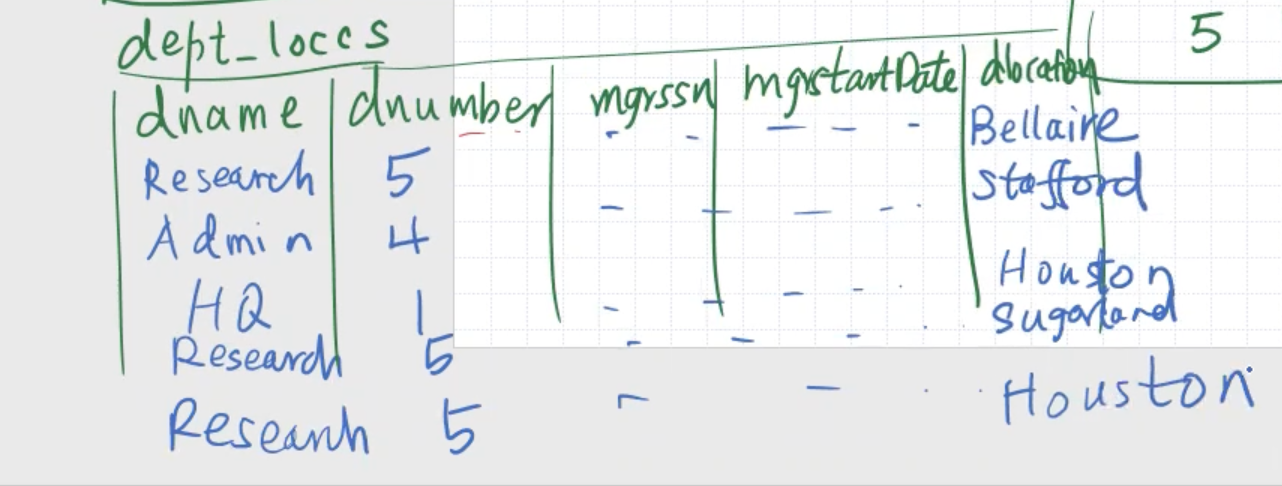
image_2021-06-16-16-00-03

Common mistakes when using join #

Its common to misuse join/natural join. Consider this example, if we have 2 entities, $R$ and $S$ :

\begin{aligned} R(a, b) && S(b, d, f) \end{aligned}

If we want to join on $b$ , we can do the natural join:

\begin{aligned} R * S \end{aligned}

While the incorrect answer is

\begin{aligned} \text{result} \leftarrow R \underset{\text{b=b}}{\bowtie} S \end{aligned}

because of ambiguity. Also, result will be a schema including 2 columns of $b$ .

If we wanted to get rid of $f$ in our joined table, we could start with a project

\begin{aligned} \text{new s} (\text{newb, d}) \leftarrow \pi_\text{b, d}(S) \end{aligned}

and then get the result with a join, because the attribute names are different now:

\begin{aligned} \text{result} \leftarrow R \underset{\text{b=newb}}{\bowtie} \text{new s} \end{aligned}

Join selectivity #

image_2021-06-16-16-11-39

Complete set of relational operations #

image_2021-06-16-16-14-58

Example queries #

image_2021-06-16-16-15-21

\begin{aligned} \text{research dept} &\leftarrow \sigma_\text{dname='Research'}(\text{ department }) \\ \text{research emps} &\leftarrow \text{research dept} \underset{\text{dnumber=dno}}{\bowtie} \text{employee} \\ \text{result} &\leftarrow \pi_\text{fname, lname, address}(\text{ research emps }) \end{aligned}

Include following exercise in weekly homework

Question: For every project located in “stafford”, list the project number, the controlling department number, and the department managers’s last name, address, and birthdate.

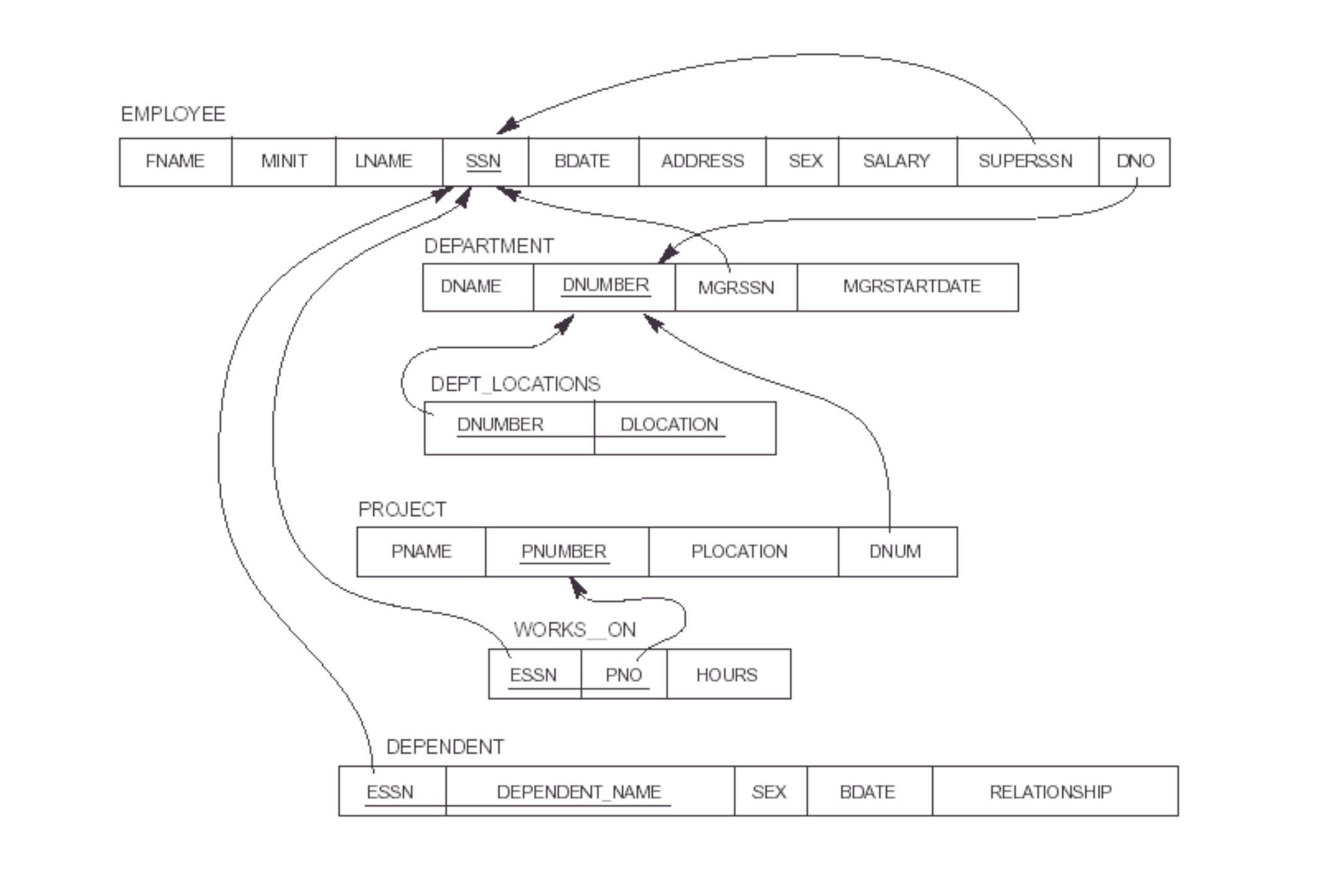
image_2021-06-10-16-56-31

\begin{aligned} \text{stafford projects} &\leftarrow \sigma_\text{plocation='stafford'}(\text{ project }) \\ \text{control dept} &\leftarrow \text{stafford projects} \underset{\text{dnum=dnumber}}{\bowtie} \text{department} \\ \text{project dept mgr} &\leftarrow \text{control dept} \underset{\text{mgrssn=ssn}}{\bowtie} \text{employee} \\ \text{result} &\leftarrow \pi_\text{pnumber, dnum, lname, address, bdate}(\text{ projec dept mgr }) \end{aligned}

image_2021-06-16-16-27-36 image_2021-06-16-16-45-57

\begin{aligned} \text{emps with deps} &\leftarrow \pi_\text{essn}(\text{ dependent }) \\ \text{all emps} &\leftarrow \pi_\text{ssn}(\text{ employee }) \\ \text{emps without deps} &\leftarrow \text{all emps} - \text{emps with deps} \\ \text{result} &\leftarrow \pi_\text{lname,fname} (\text{emps without deps} * \text{employee}) \end{aligned}

Note: employee and emps with deps must be union compatible to take the difference.

Another exercise with the same schema

Include following exercise in weekly homework

List the names (first name, last name) of managers who have at least one dependent.

First approach uses set operations:

\begin{aligned} \text{mgr(ssn)} &\leftarrow \pi_\text{mgrssn} (\text{ department }) \\ \text{emp with dep(ssn)} &\leftarrow \pi_\text{essn} (\text{ dependent }) \\ \text{mgr with deps} &\leftarrow \text{mgr} \cap \text{emp with deps} \\ \text{result} &\leftarrow \pi_\text{lname, fname} (\text{mgr with deps} * \text{employee}) \end{aligned}

Another approach using join:

\begin{aligned} \text{mgr dep} &\leftarrow \pi_\text{essn} (\text{department} \underset{\text{mgrssn=essn}}{\bowtie} \text{dependent}) \\ \text{emp mgr dep} &\leftarrow \text{employee} \underset{\text{ssn=essn}}{\bowtie} \text{mgr dep} \\ \text{result} &\leftarrow \pi_\text{fname, lname} (\text{ emp mgr dep }) \end{aligned}