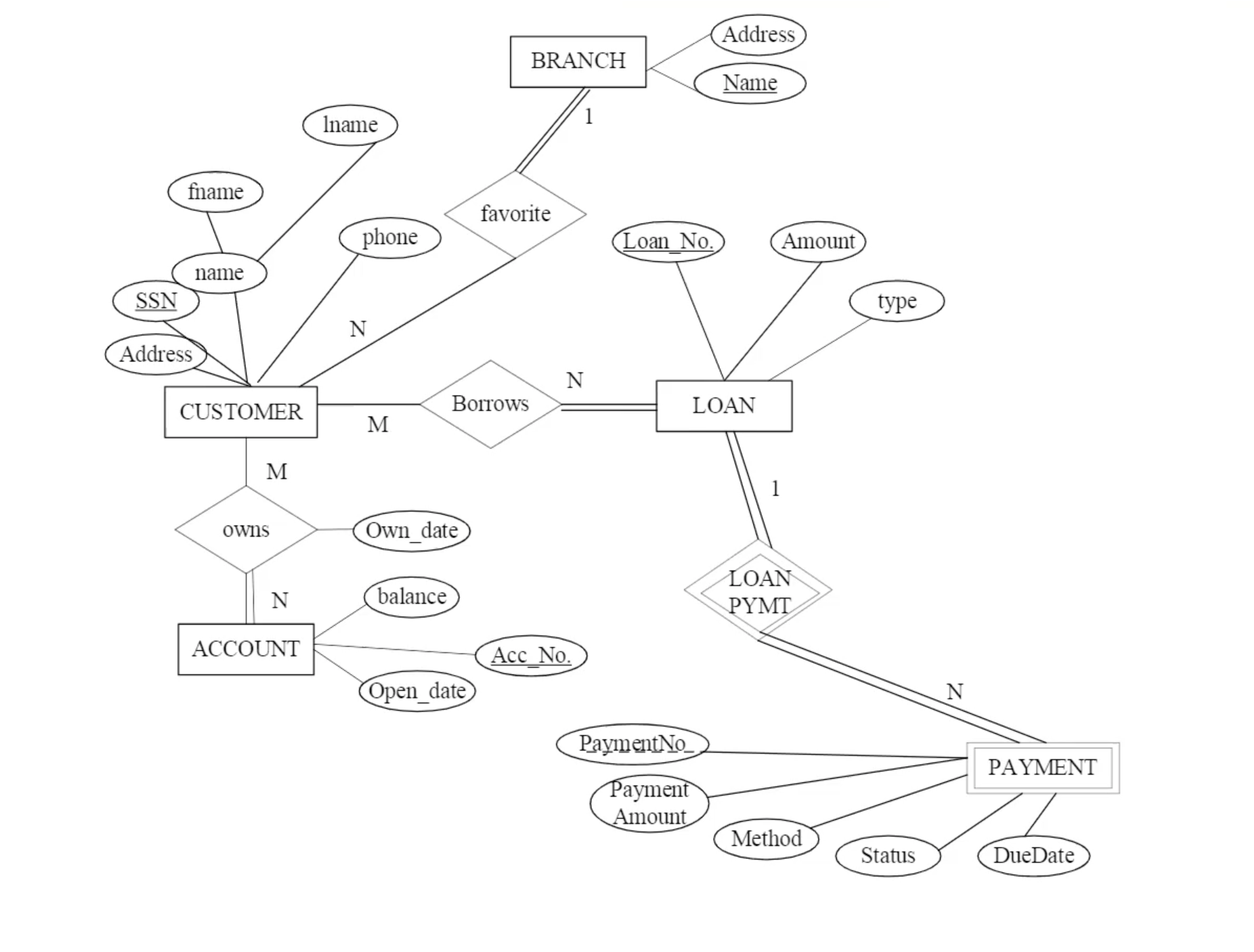
Assignment 1 solution #
Relational algebra cont. #
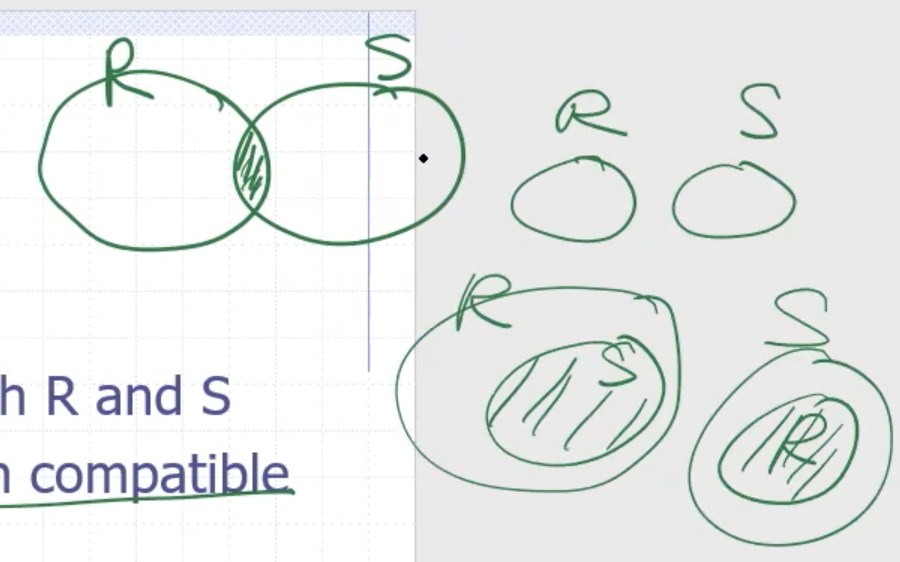
Intersection #

They must be union compatible.
Include in weekly homework.
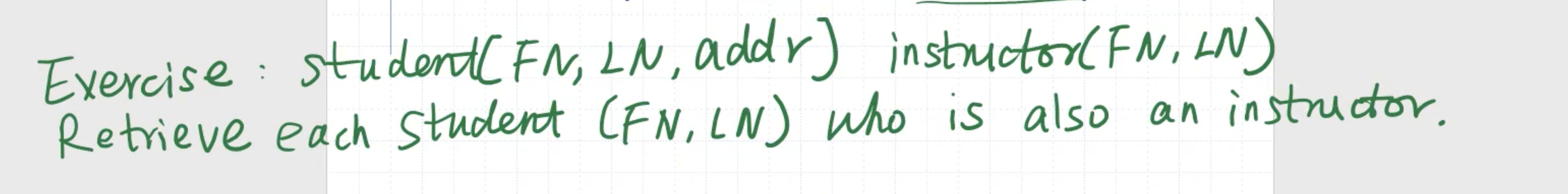
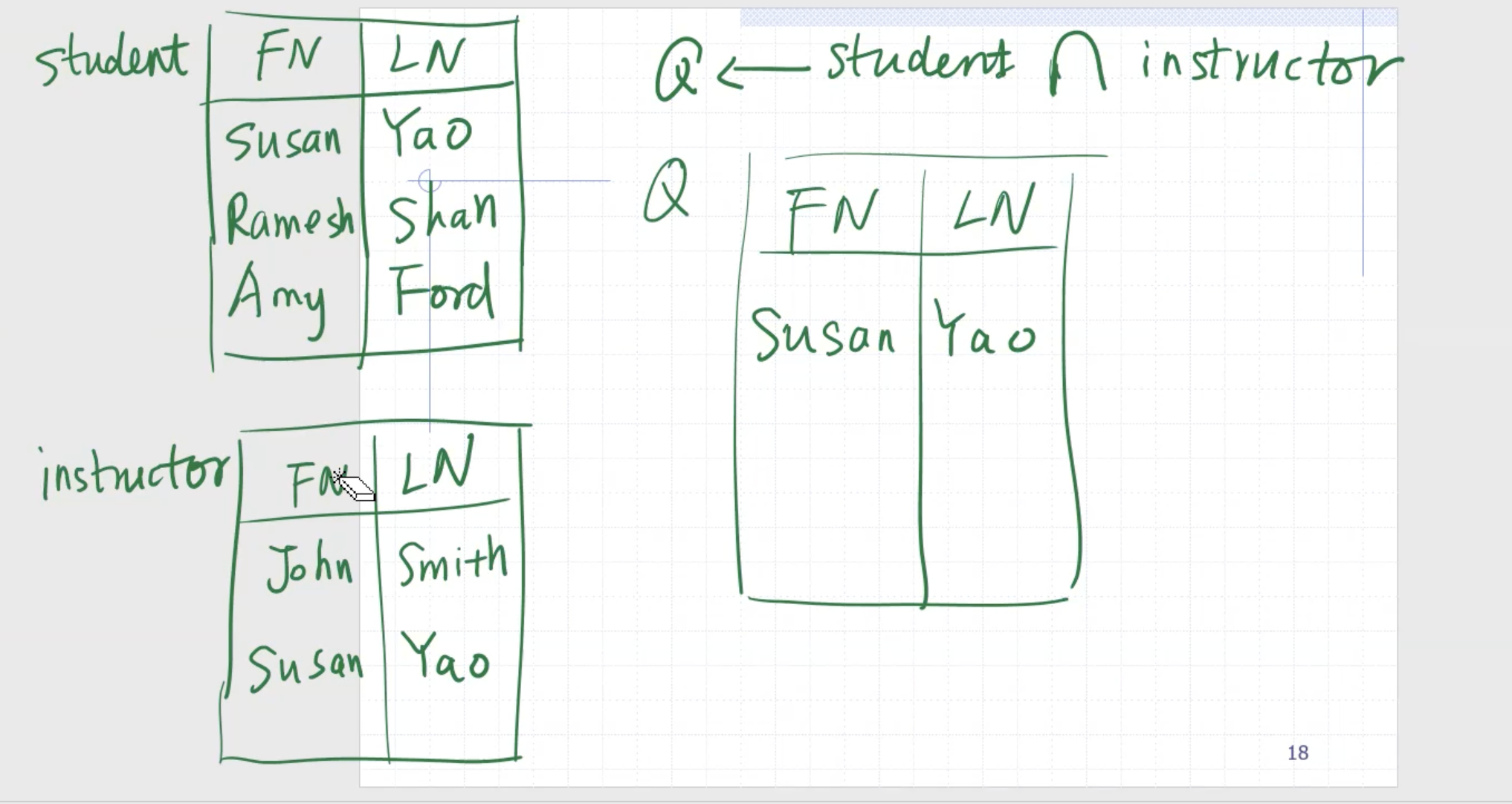
Set difference #

Must be union compatible.

The result is a new relation with the same schema.
\[\begin{aligned} a \leftarrow \text{student} - \text{instructor} \end{aligned}\]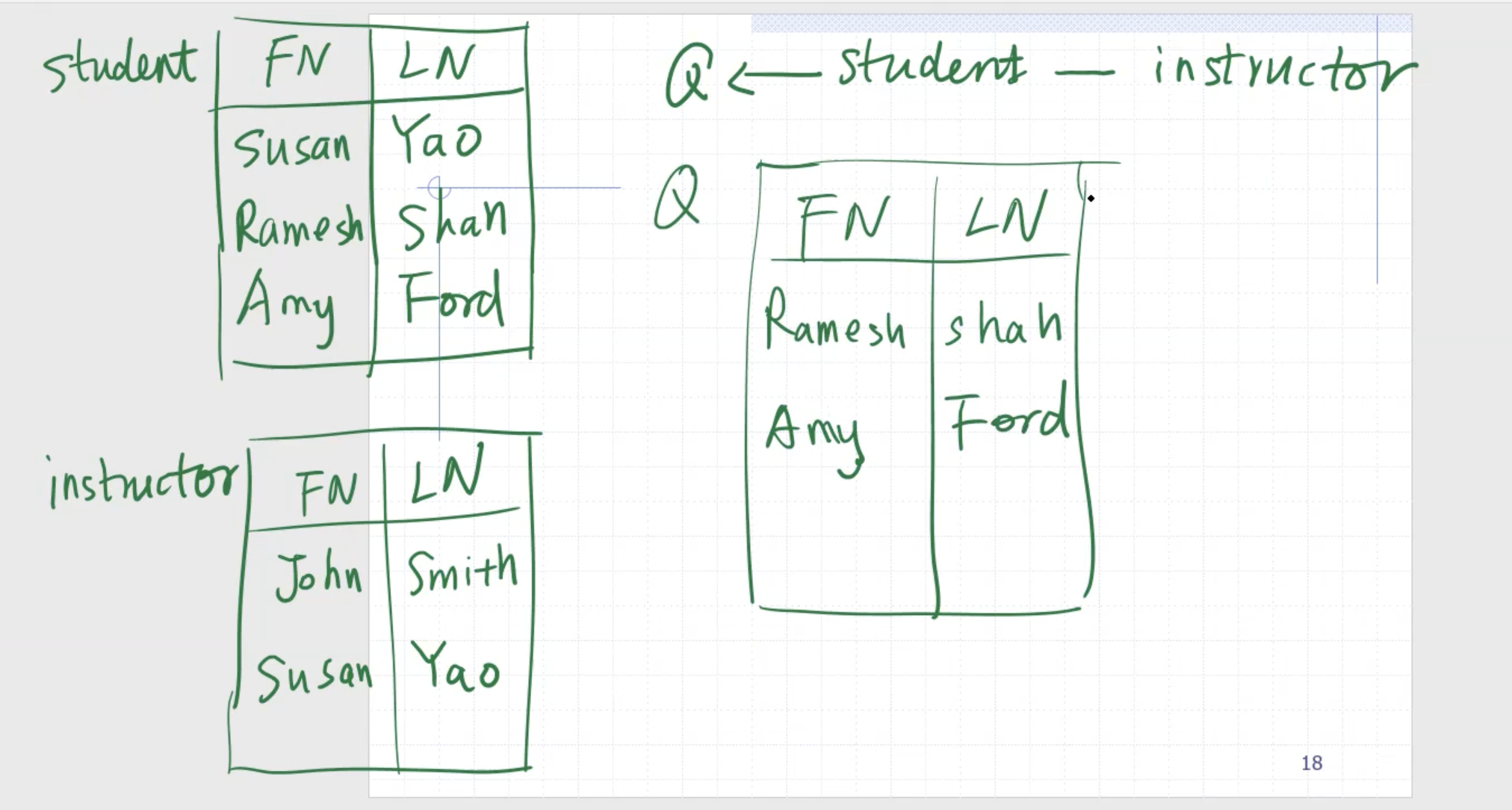
This returns only John Smith.
Common properties #

Cartestian product #

The results from \( R \) and \( S \) are combined.
For example
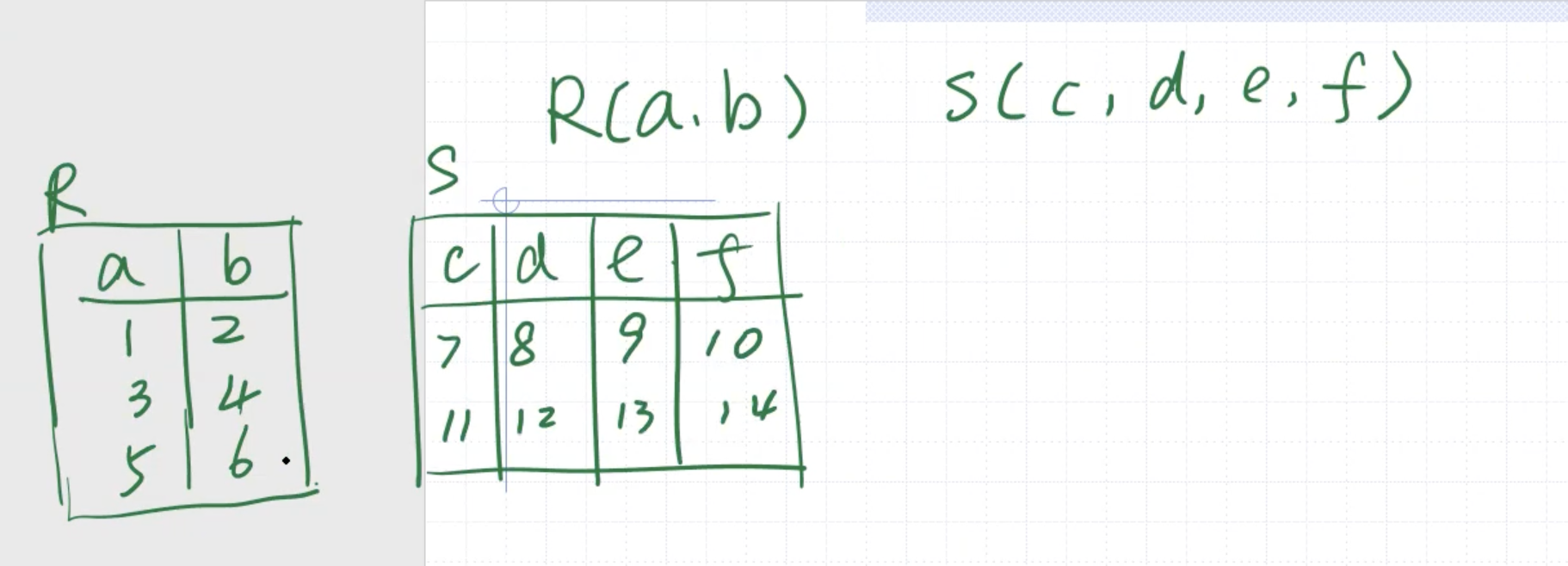
Note: \(R\) and \(S\) are of different schema.
It is the combination of the first row of \( R \) with each row of \( S \) ,
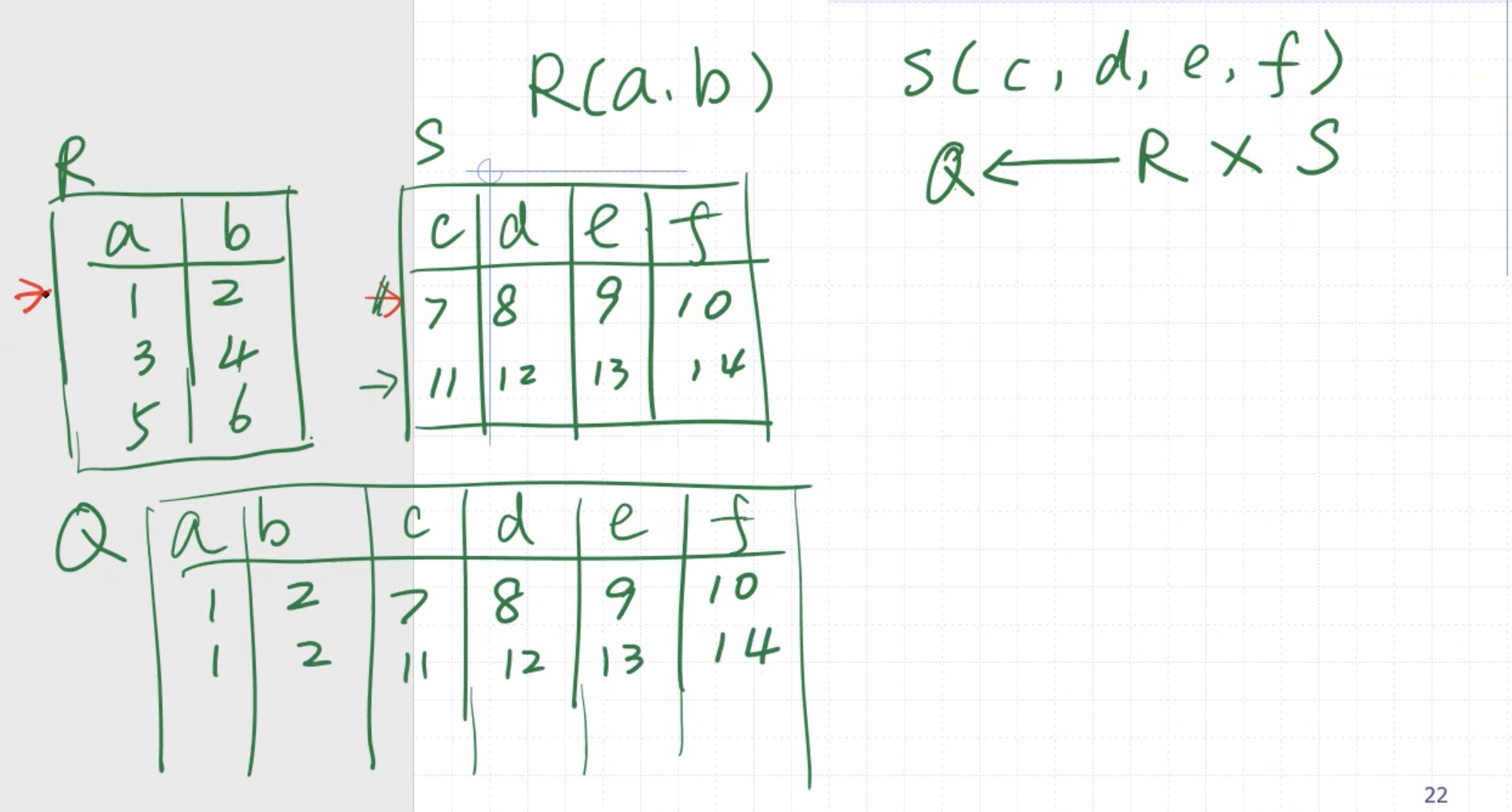
and it continues
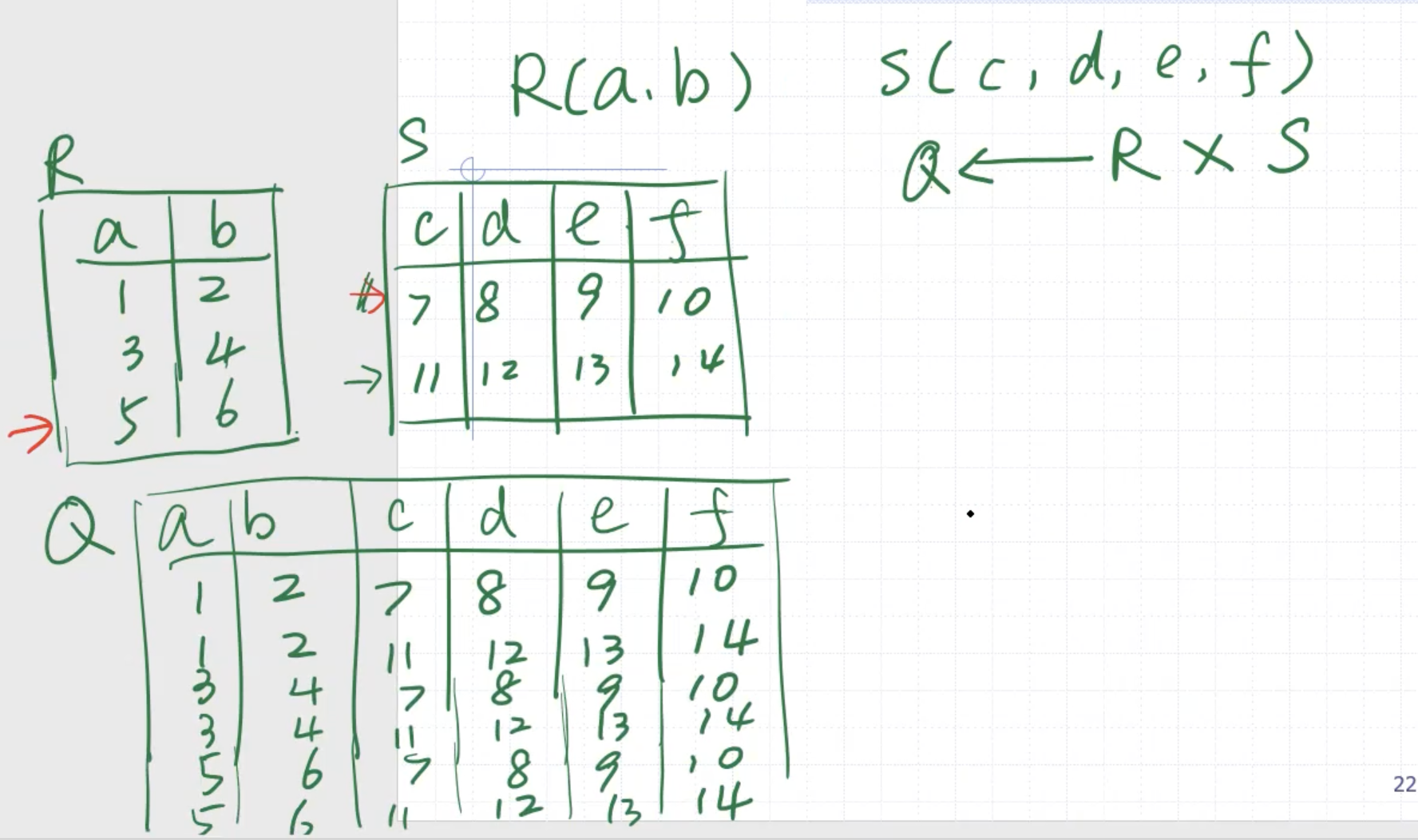
For our amount of tuples (exhaustive combination):
\[\begin{aligned} n_R = 3 \\ n_S = 2 \\ 3 \times 2 = 6 \end{aligned}\]Another example

Use our given employee/department/etc schema for this problem.
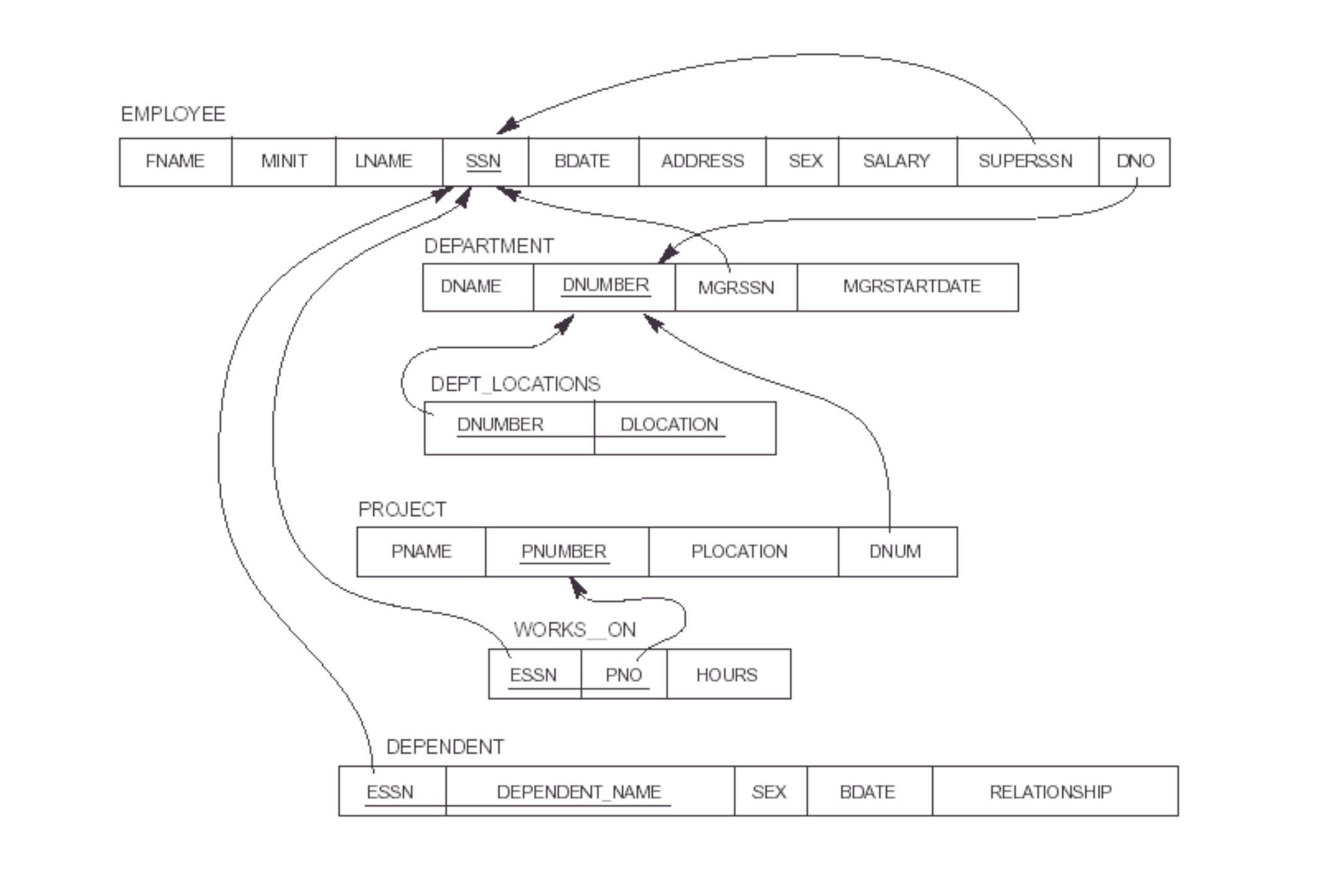
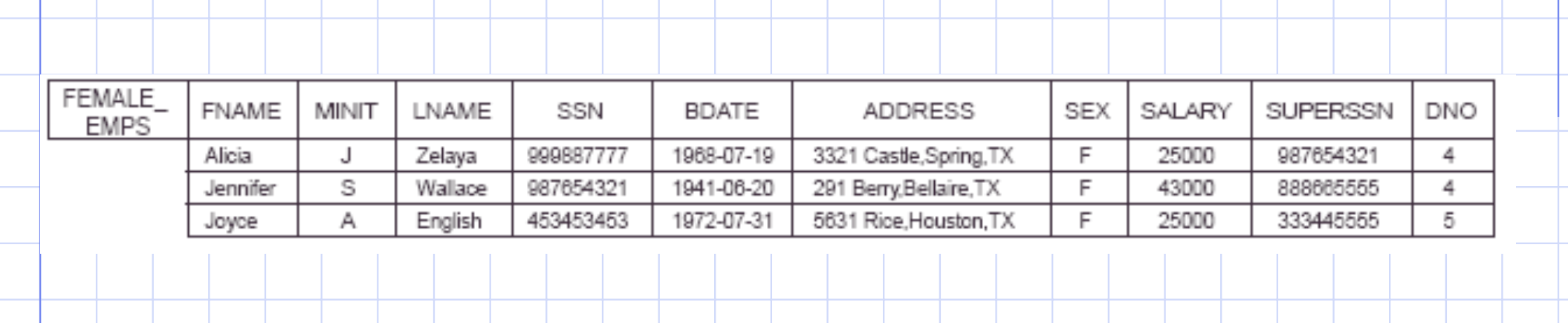

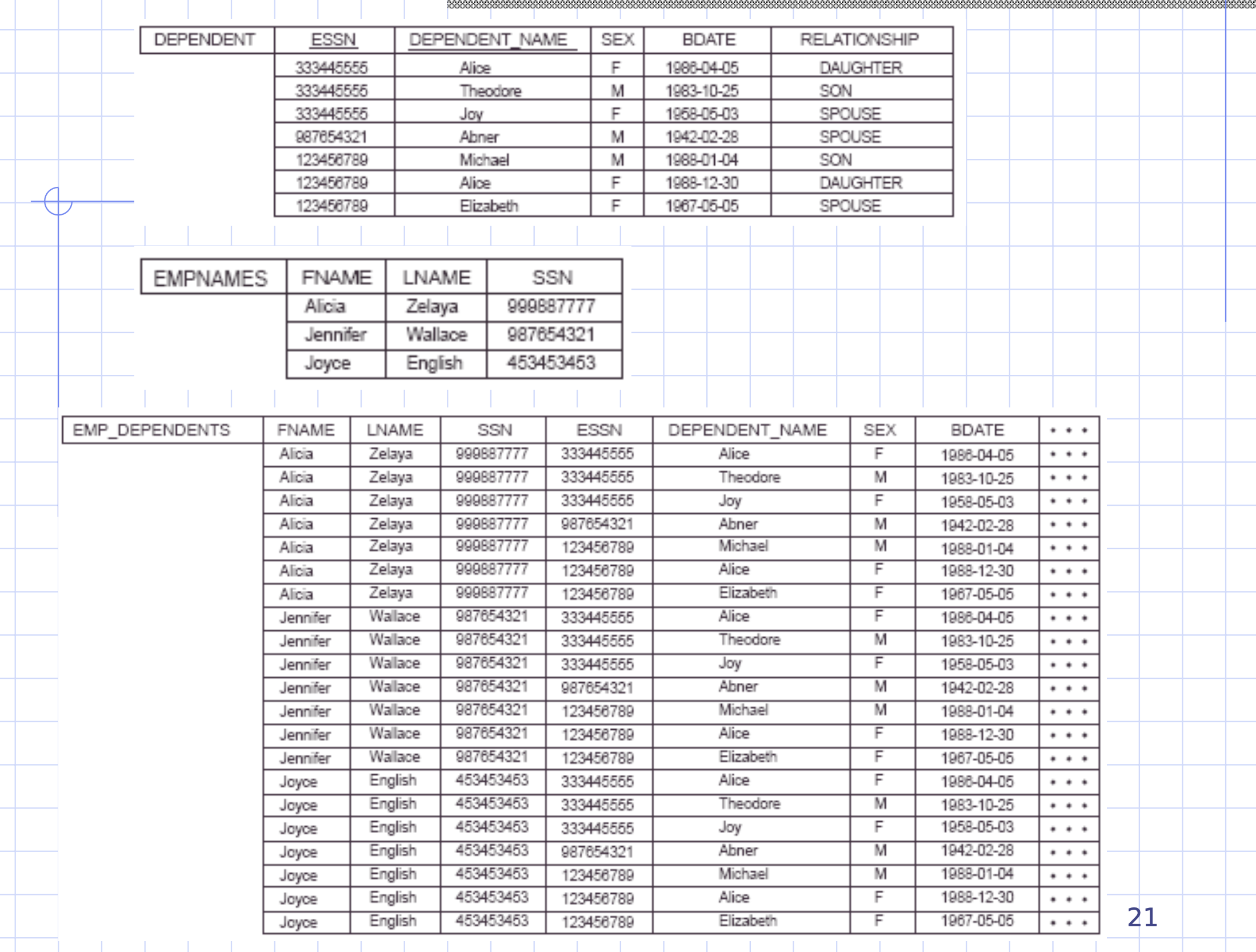
Many of these combinations are meaningless right now.
The actual employee/dependent combinations are when ssn == essn, so we need to do a selection
Finally, we can project to get the done result
\[\begin{aligned} \text{result} \leftarrow \pi_\text{fname, lname, dependent name}(\text{ actual dependents }) \end{aligned}\]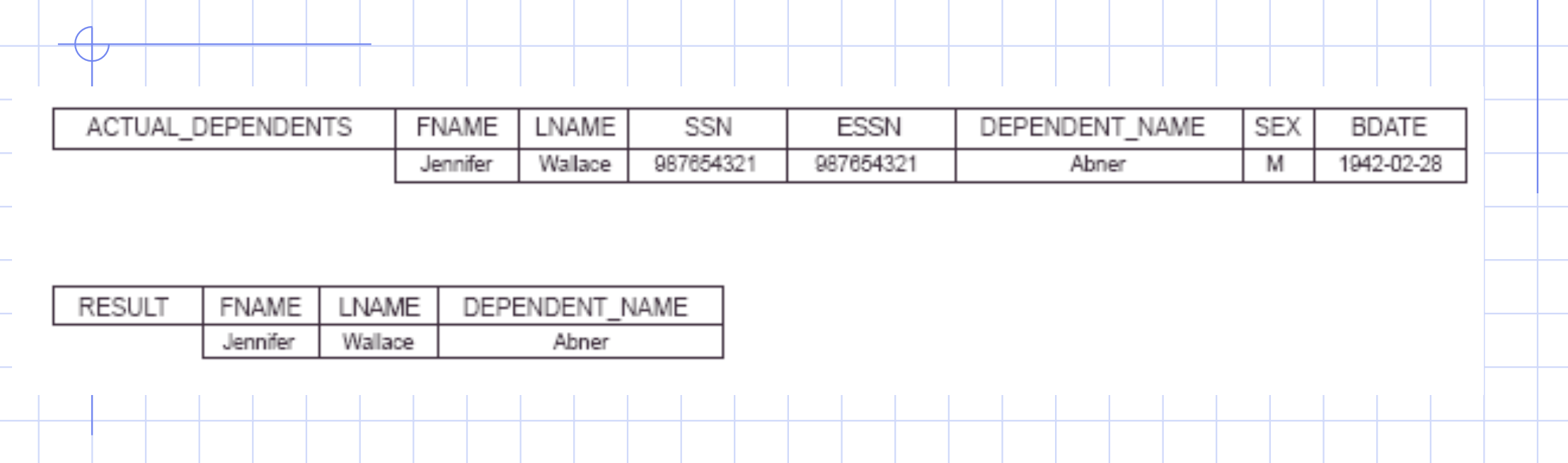
JOIN operation
#

It is the combination of a cartesian product followed by a selection.
So, looking back at our previous example
\[\begin{aligned} \text{actual dependents} \leftarrow \text{emp names} \underset{\text{ssn=essn}}{\bowtie} \text{dependents} \end{aligned}\]It starts on the first employee, and combines with the first dependent. But we do not output to a intermediary table. It then checks if the condition is true, otherwise it ignores the tuple. It follows this same process and builds the result table.

Conditions
- have comparison
- can be combined using and/or

When we only have 1 condition with an equal size, it is called an equijoin, for example
\[\begin{aligned} \text{dept manager} \leftarrow \text{department} \underset{\text{mgrssn=ssn}}{\bowtie} \text{employee} \end{aligned}\]An equijoin is guaranteed to have one or more pairs of attributes that have identical values (despite possibly not being named the same thing). If we throw out the duplicates, it is called a natural join.

When the natural join is performed, any attributes with duplicate names are removed.
You could not perform this same join operation with the standard join operation \[ \underset{\text{dnumber=dnumber}}{\bowtie} \] because there is ambiguity.
Note on notation: the asterisk \(*\) is used to indicate natural join.