Announcements
- Assignment 2 is posted
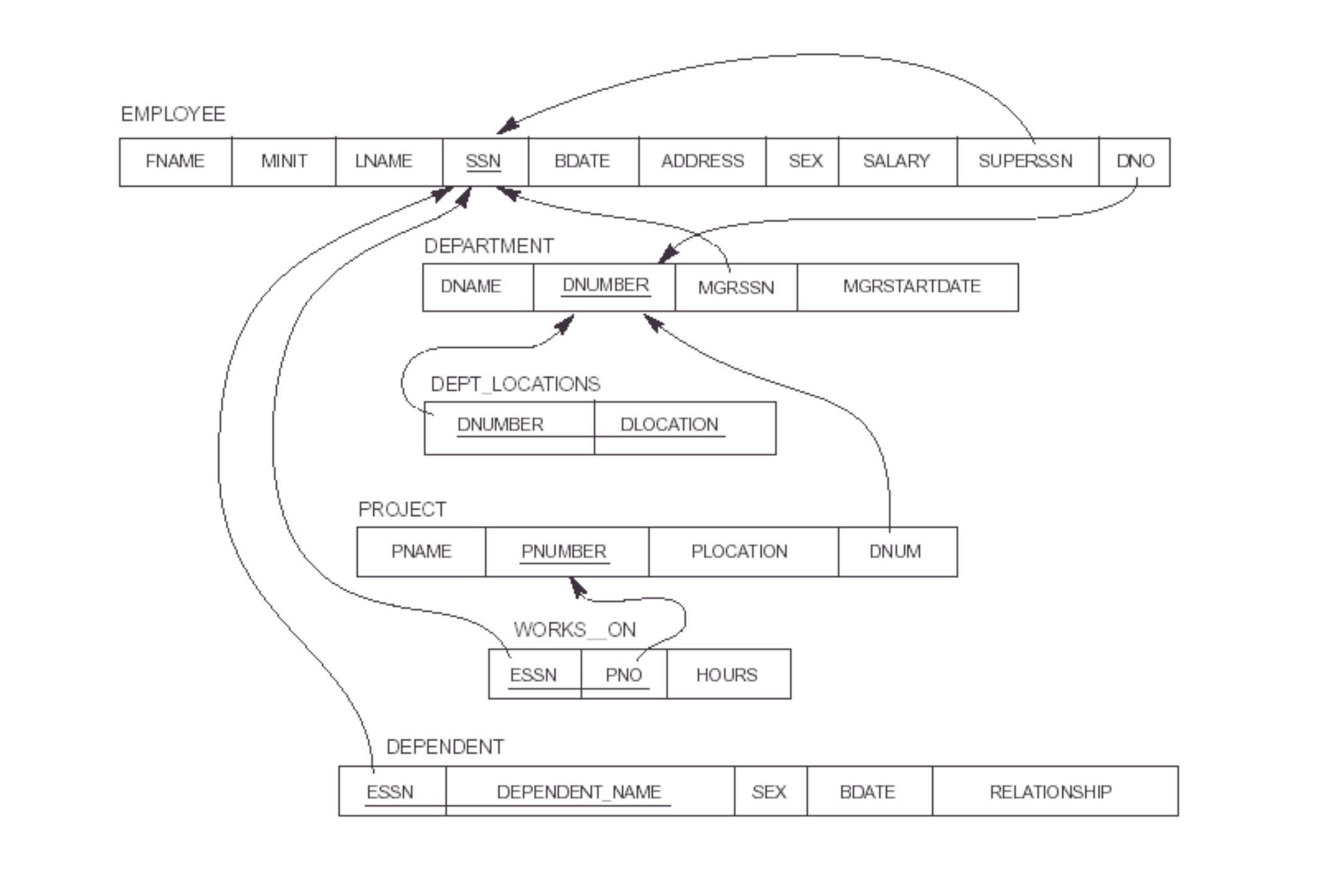
Relational algebra cont. #
SELECT cont.
#

When cascaded: the conditions can be in different order but they will produce the same output. The conditions can be connected by logical and.
If we compose 2 select operations
\[\begin{aligned} \sigma_{\text{salary } > 7300} ( \sigma_{\text{dno = } 5 } (\text{ employee })) \end{aligned}\]We can combine the 2 conditions with a logical and
\[\begin{aligned} \sigma_{\text{salary > 7300} \text{ and } \text{ dno } = 5 } (\text{ employee }) \end{aligned}\]Selection is a filter, so the input schema is the same as the output schema, however the number of tuples is equal to or less than the input.
Exercise #
This is part of the weekly exercise homework.
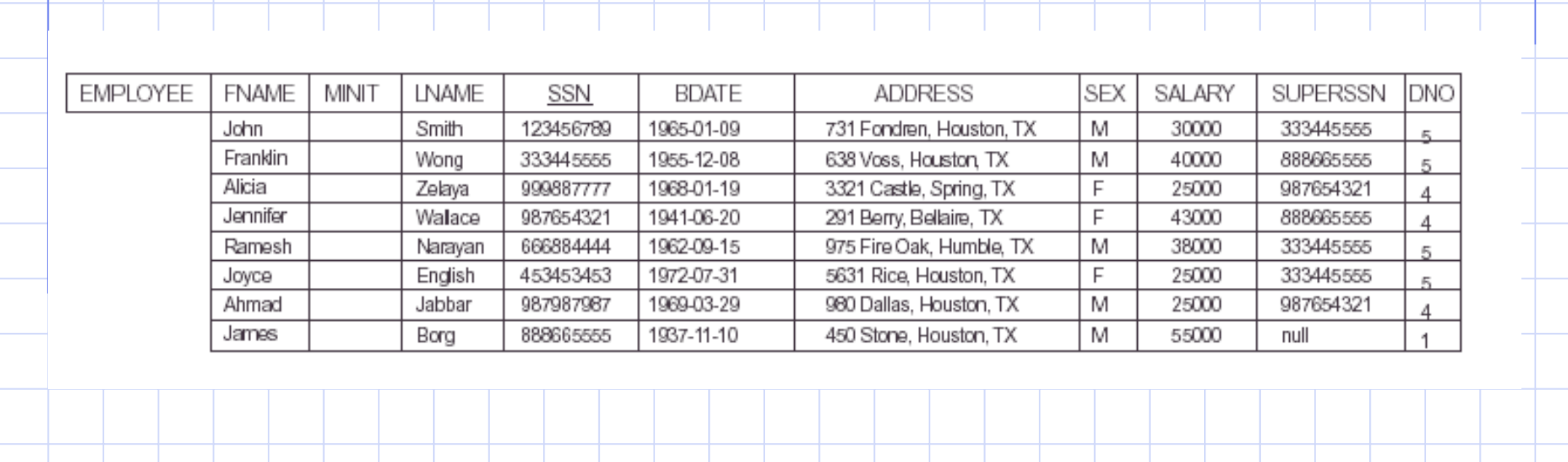
-
Retrieve each female employee \[\begin{aligned} \text{result} \leftarrow \sigma_{\text{ sex = 'F' }} ( \text{ employee }) \end{aligned}\]
-
Retrieve each female employee whose salary is greater than 30000 \[\begin{aligned} \text{result} \leftarrow \sigma_{\text{ sex = 'F' and salary > 30000}} ( \text{ employee }) \end{aligned}\]
Projection operation #

In the projection operation, the input schema can be different than the output schema. It allows you to select certain columns and discard the other ones.
Projection is notated using \( \pi \) , for example
\[\begin{aligned} \pi_{\text{<list>}}(R) \end{aligned}\]Where
- \( \text{list} \) is a list of attributes, and
- \( R \) is the entity
For example,
\[\begin{aligned} \text{result} \leftarrow \pi_\text{<fname, lname, ssn>} (\text{ employee }) \end{aligned}\]Note that the output schema only has 3 columns.
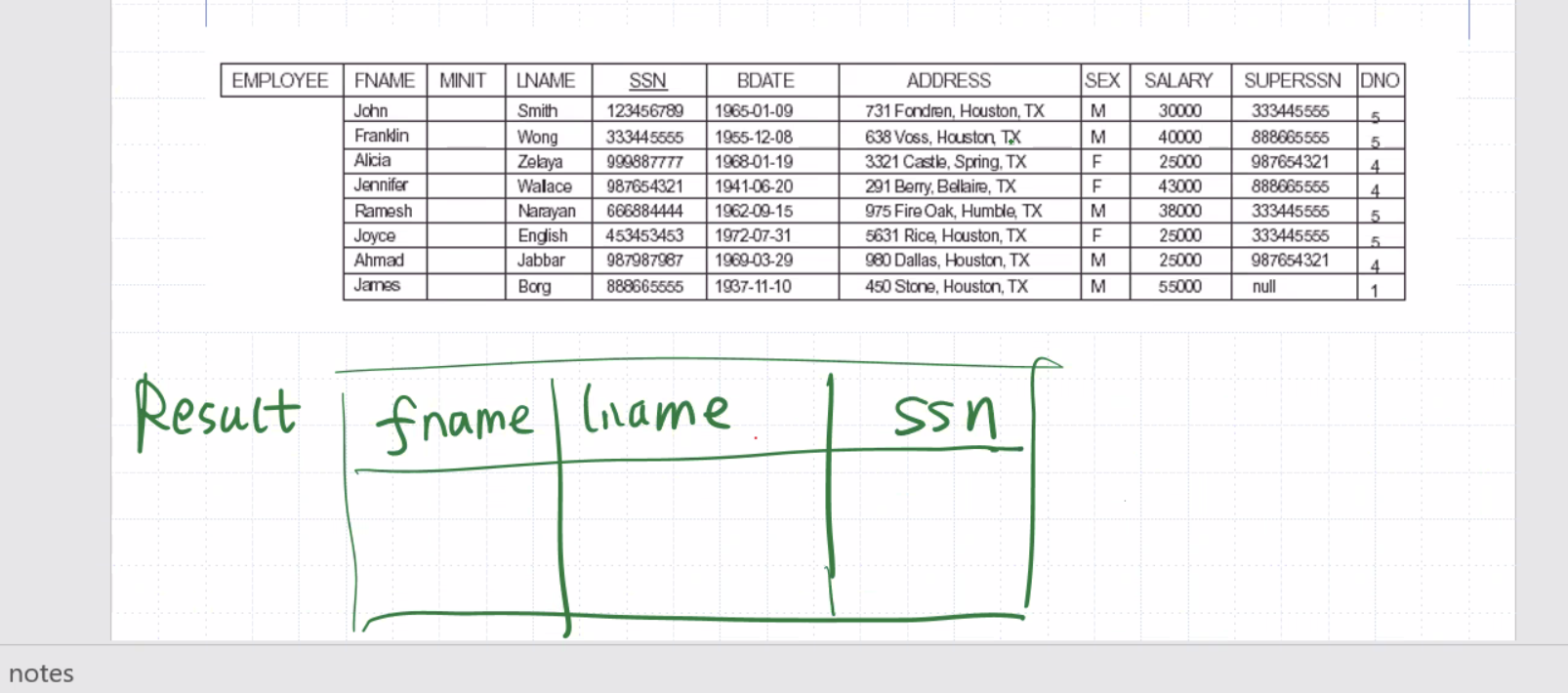
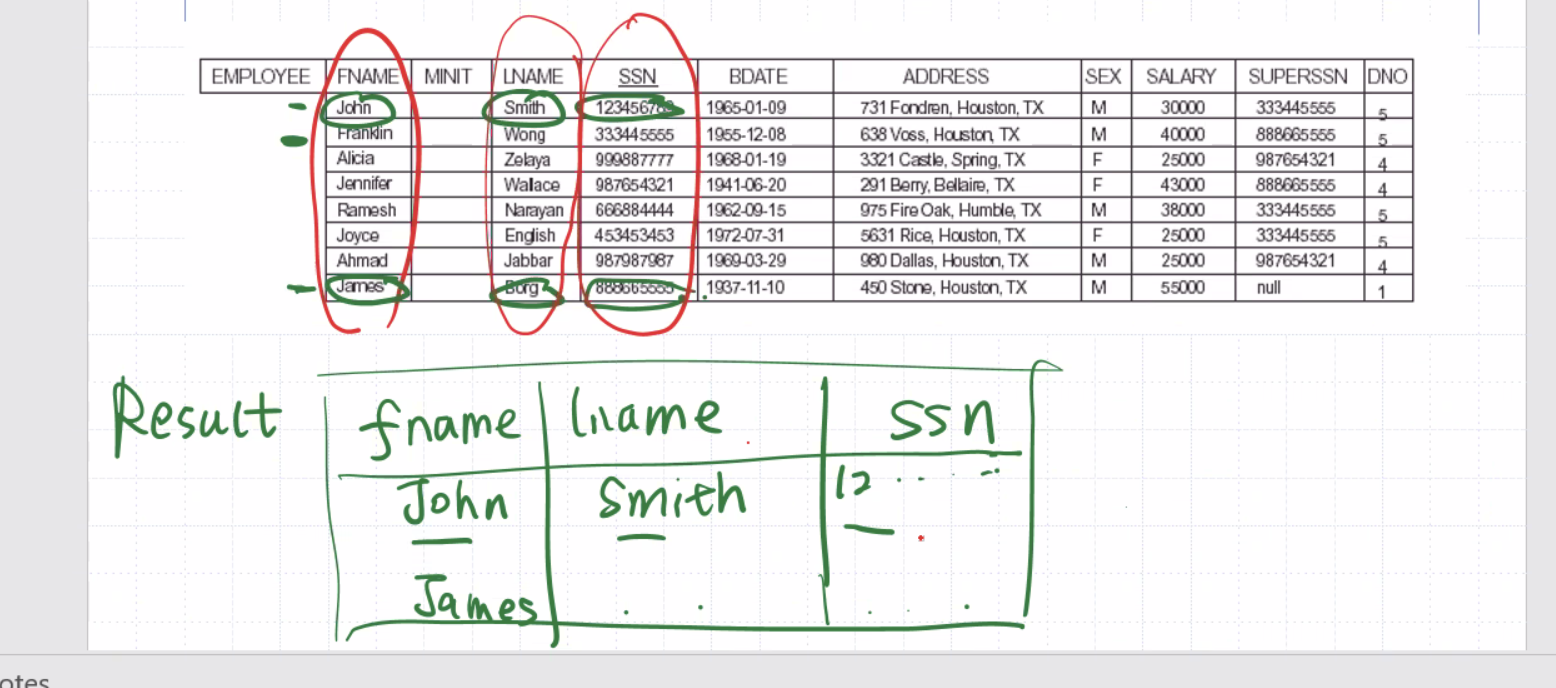
Consider
\[\begin{aligned} \text{result} \leftarrow \pi_\text{<salary>} (\text{ employee }) \end{aligned}\]Our result will only have 1 columns.
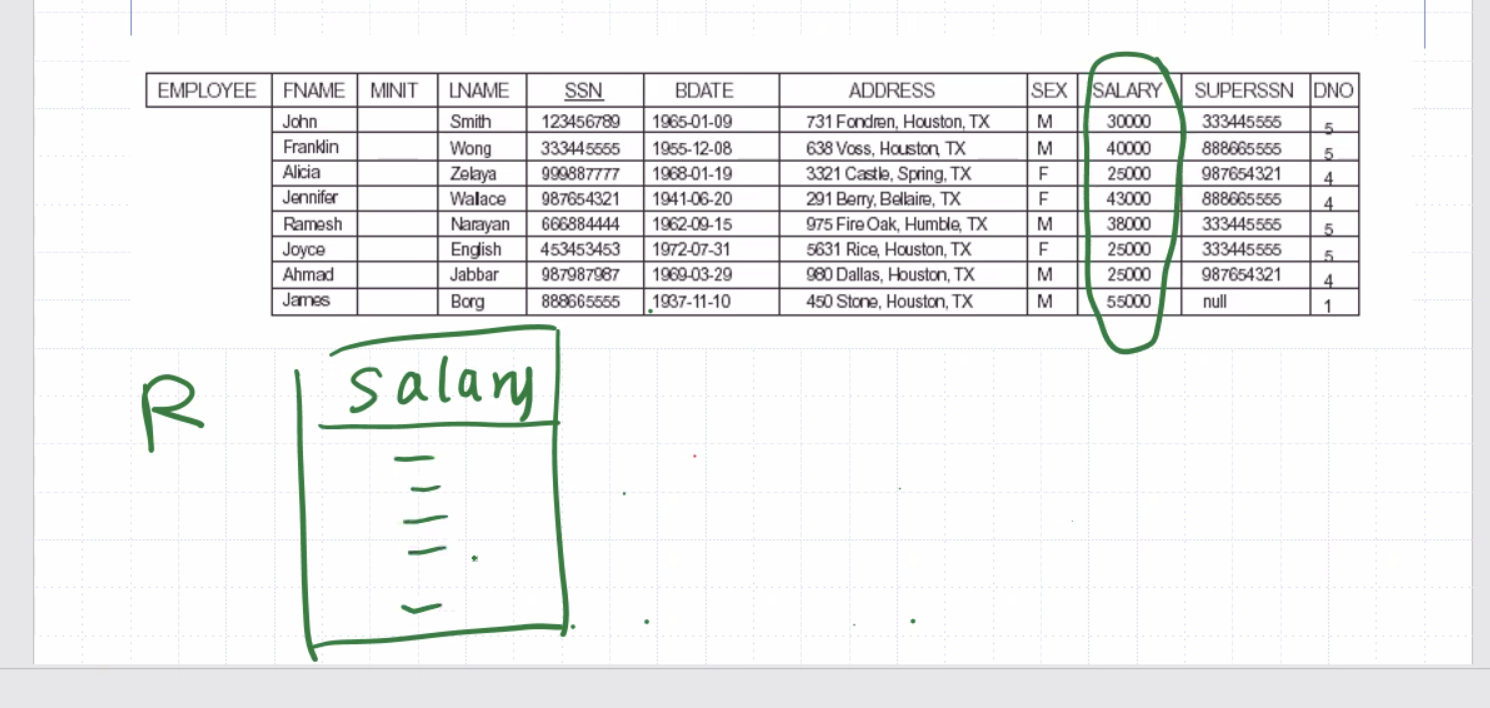
We have 8 tuples, but 3 of them are 25000 (duplicates). By definition, relational model is set based (and so relational algebra is too), so we do not allow duplicate tuples. Any duplicate tuples will be removed in the returned table.

The attributes in the list must be a subset of the attributes of the entity.
The last projection is what really matters,
\[\begin{aligned} \text{result} &\leftarrow \pi_\text{<fname>}(\pi_\text{<ssn, fname>} (\text{ employee })) \\ &= \pi_\text{<fname>} (\text{ employee }) \end{aligned}\]Sequence of operations #
If we want to compose selection and projection:

Rename operation #

We can use this operator to rename the output of an expression.

If \( R \) is a relation, we can rename the relation to \( S \) , and/or rename the attributes name one by one.
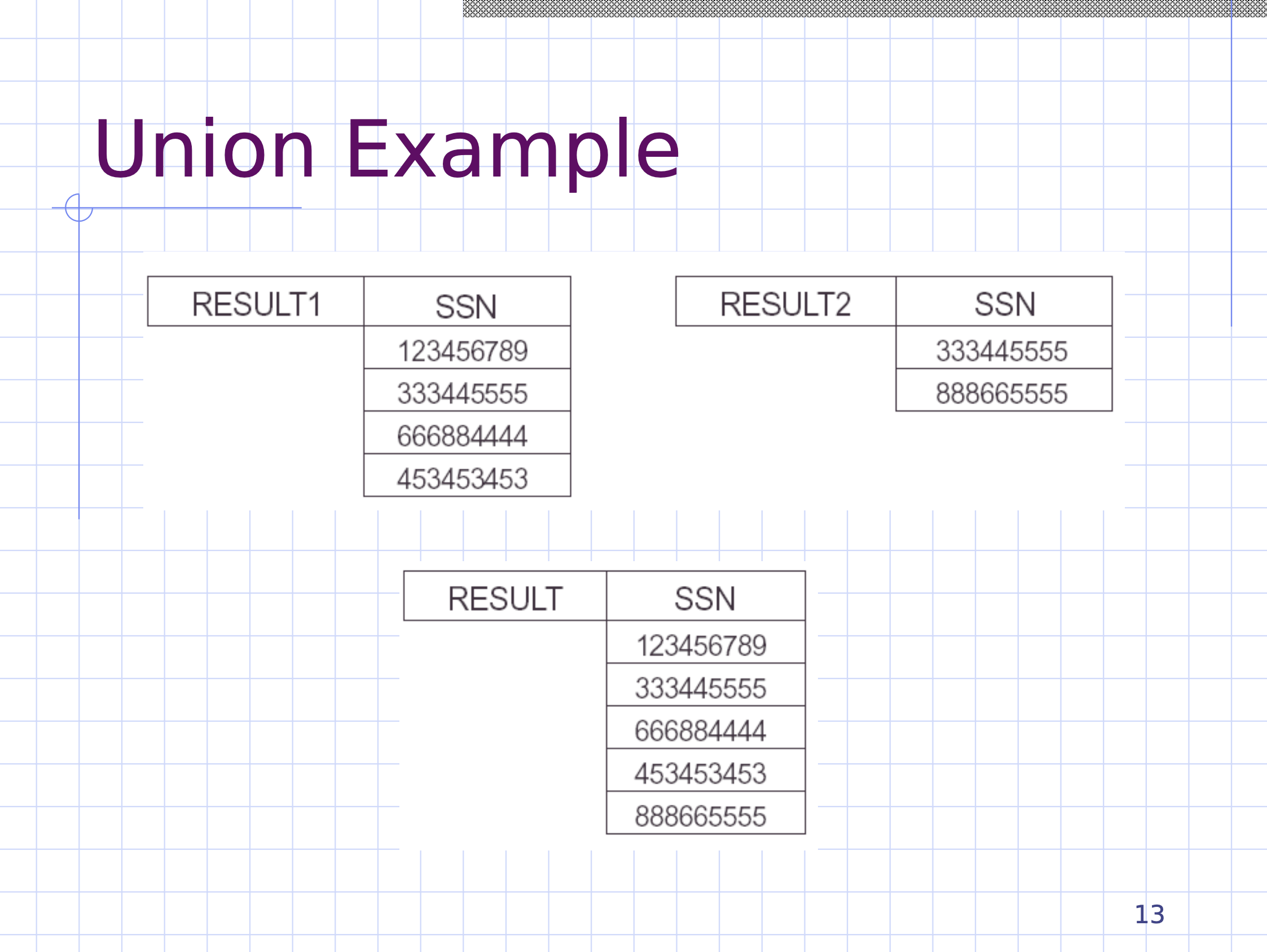
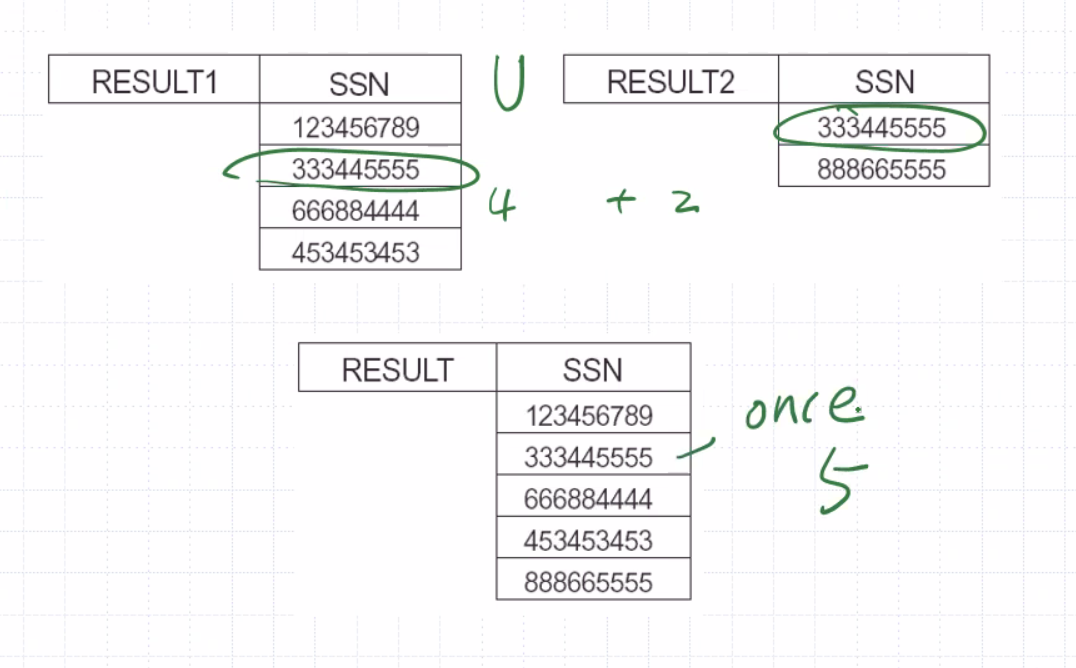
\[\begin{aligned} &\text{R} \leftarrow \pi_\text{<fname, lname, salary>} (\text{ employee }) \\ & \rho_\text{S (fn, ln, sal)} (\text{R}) &\text{new relation named S}\\ & \rho_\text{(fn, ln, sal)} (\text{R}) &\text{new relation still named R}\\ & \rho_\text{S}(\text{R}) &\text{new relation named S}\\ &&\text{ but no new attribute names} \end{aligned}\]Union operator #


No duplicates allowed, it is a set.
For example,

Example
