Exercise solutions #

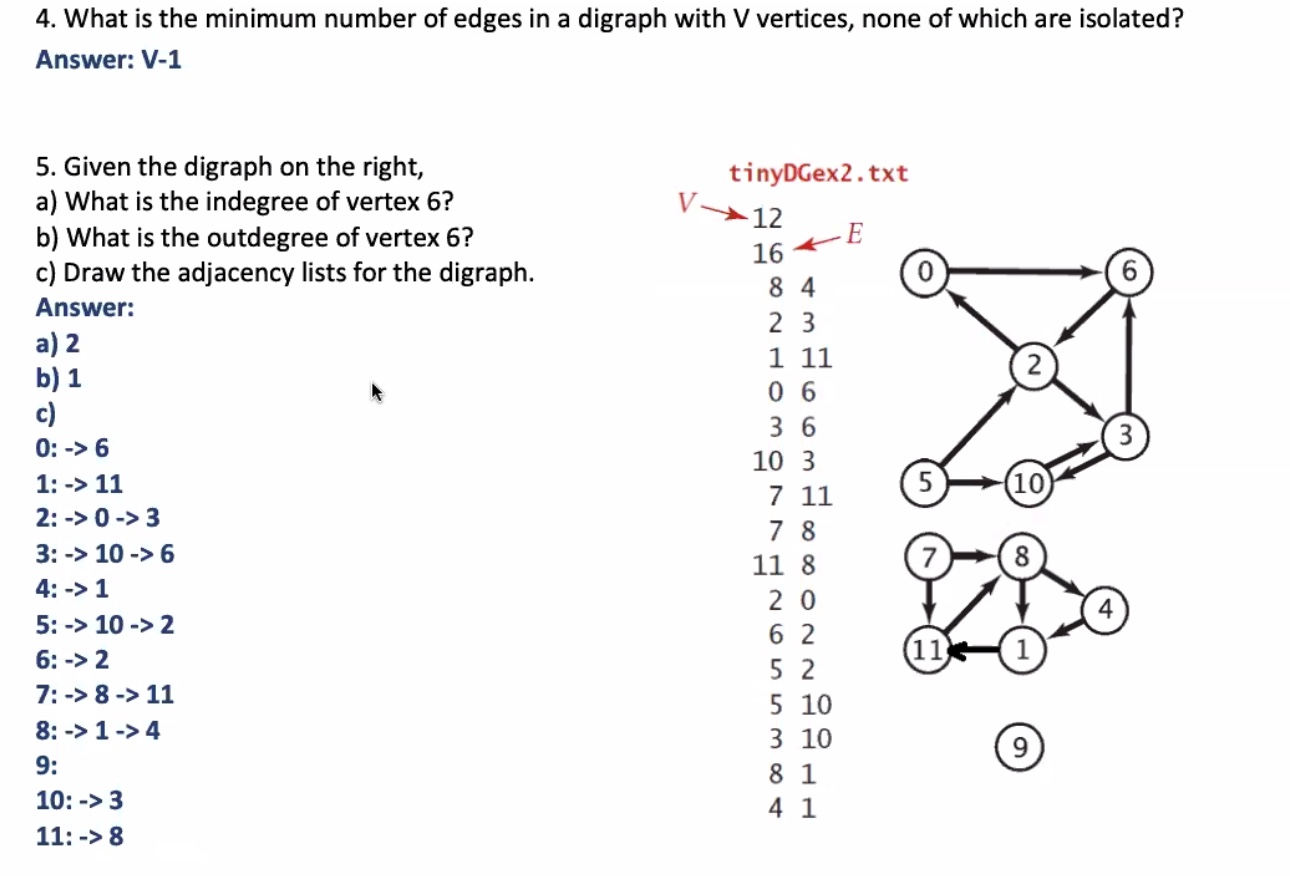
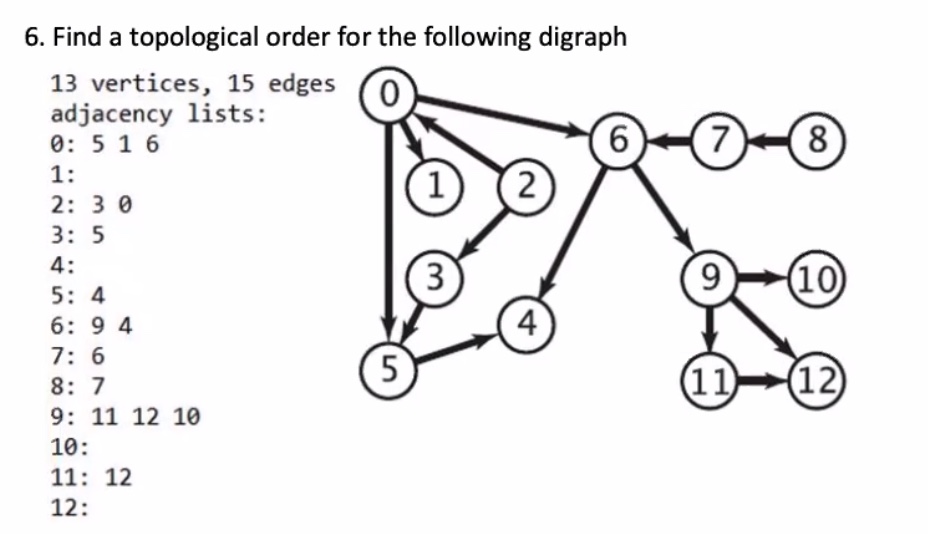
On the whiteboard:

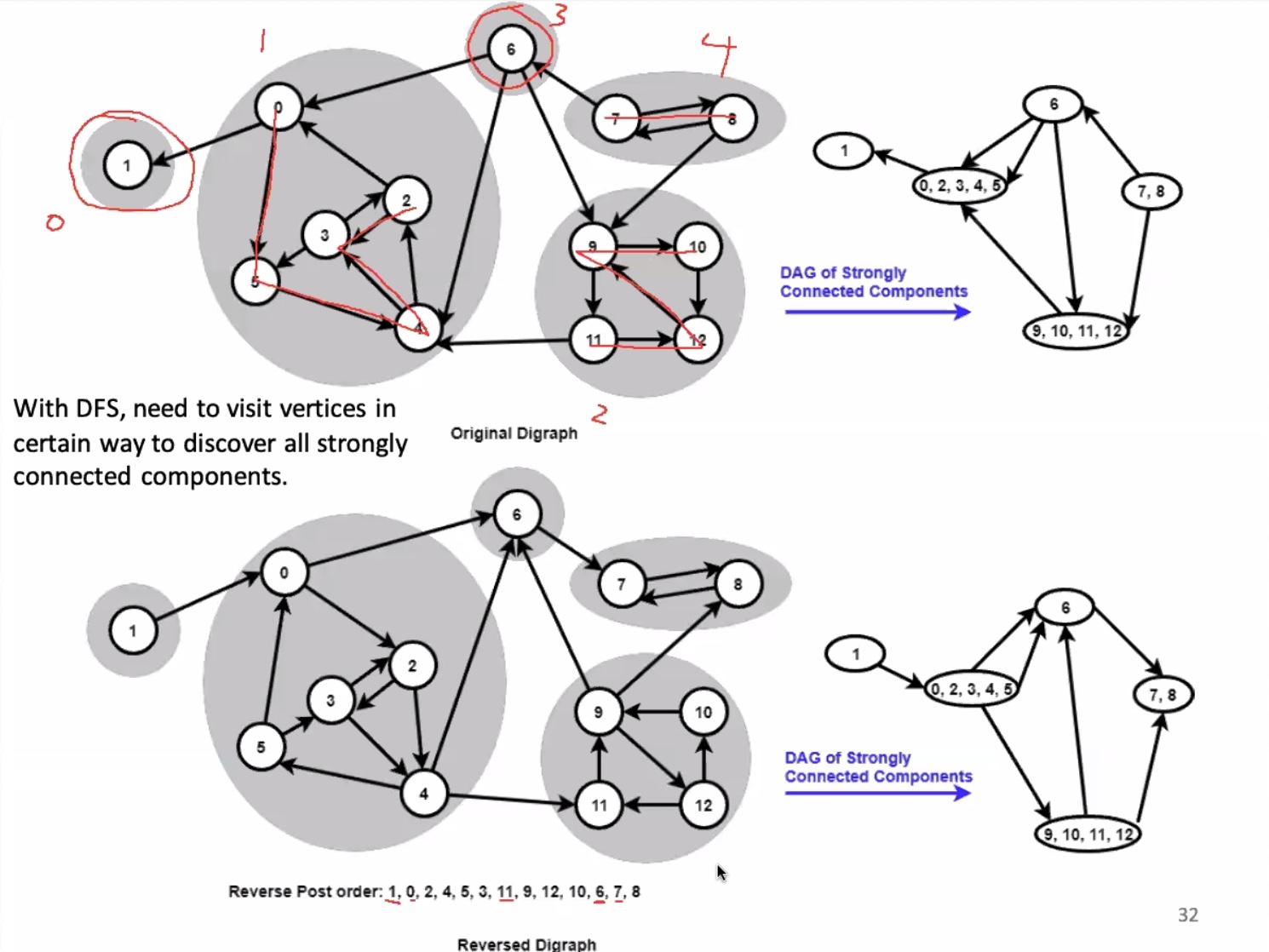
Start on vertex 0

Move onto vertex 2, need to exhaust all vertices

Move onto vertex 7

The reverse post order is : 8, 7, 2, 3, 0, 6, 9, 10, 11, 12, 1, 5, 4

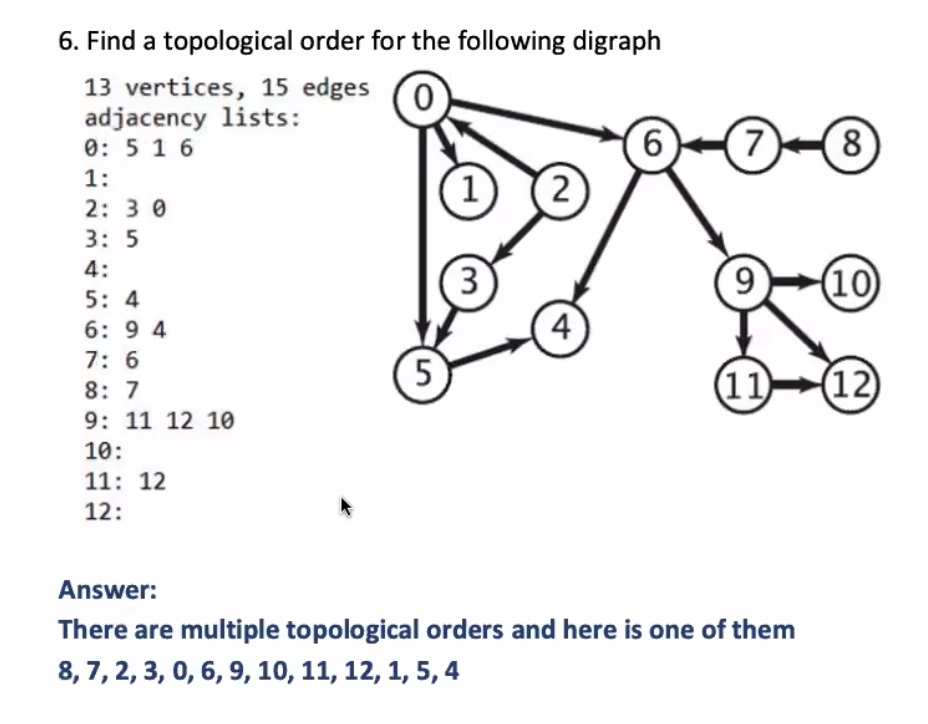
Graph cont. #

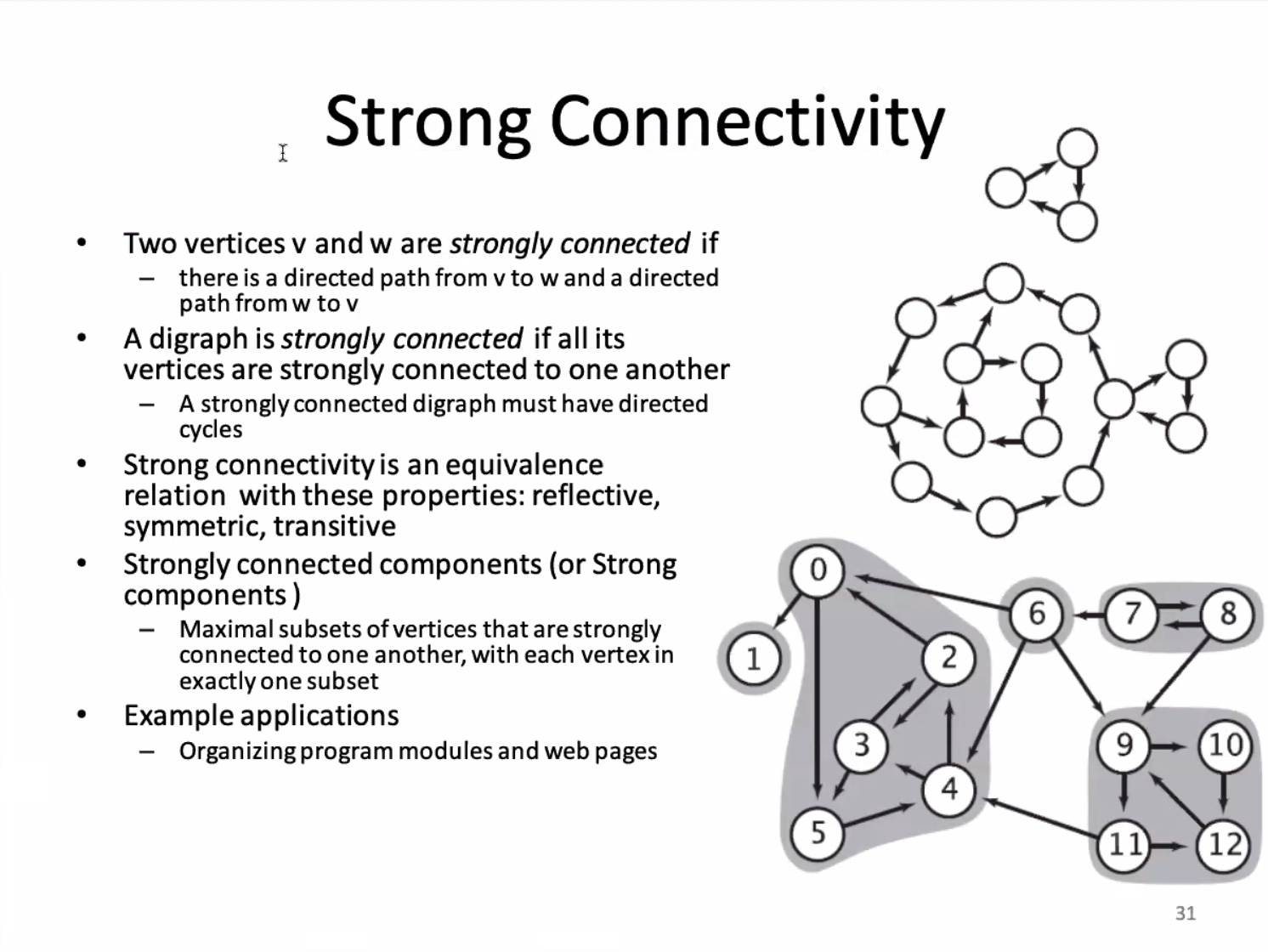
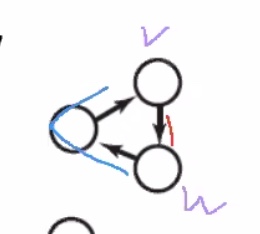
These are considered strongly connected. Also considered a strongly connected digraph.

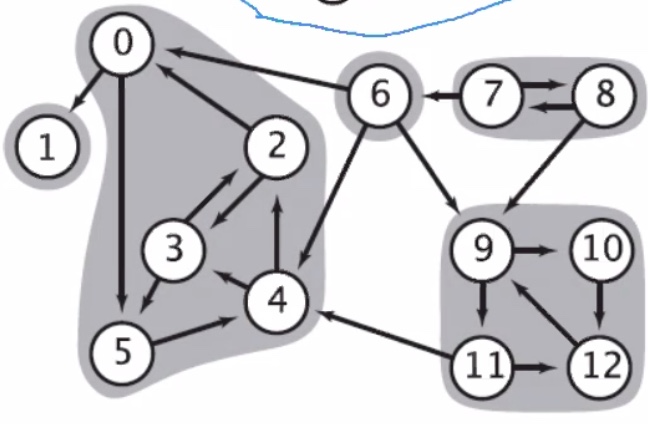
5 strongly connected components.

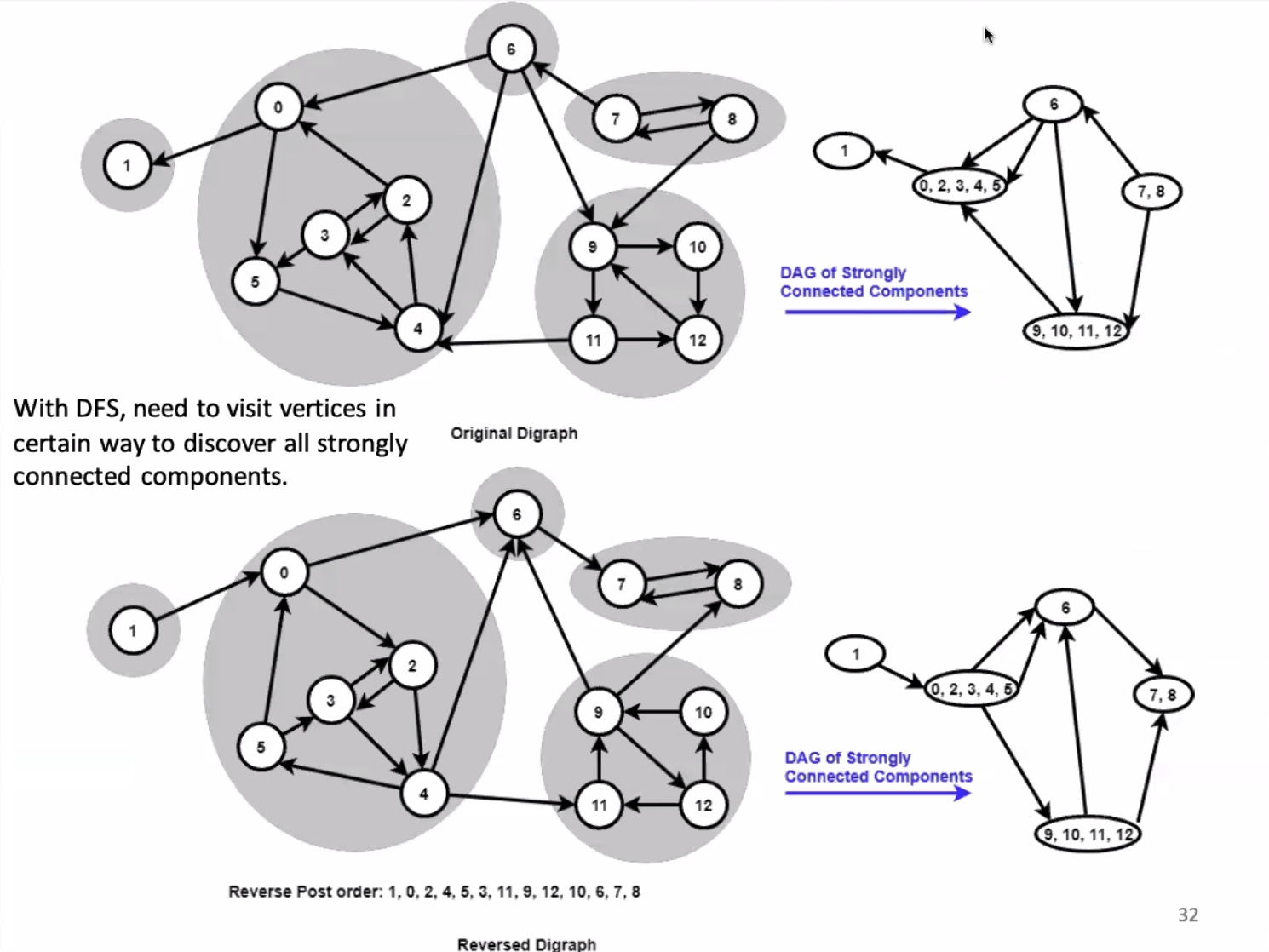
Reversed graphs are still strongly connected in the same components. A reversed graph’s reverse post order will show each component. Visit each vertex in the reverse post order and keep track of which ones have been visited, each vertex will be able to reach all the other vertex in the same component.

A strongly connected digraph has 1 strong component.

A DAG has (V) strong components.

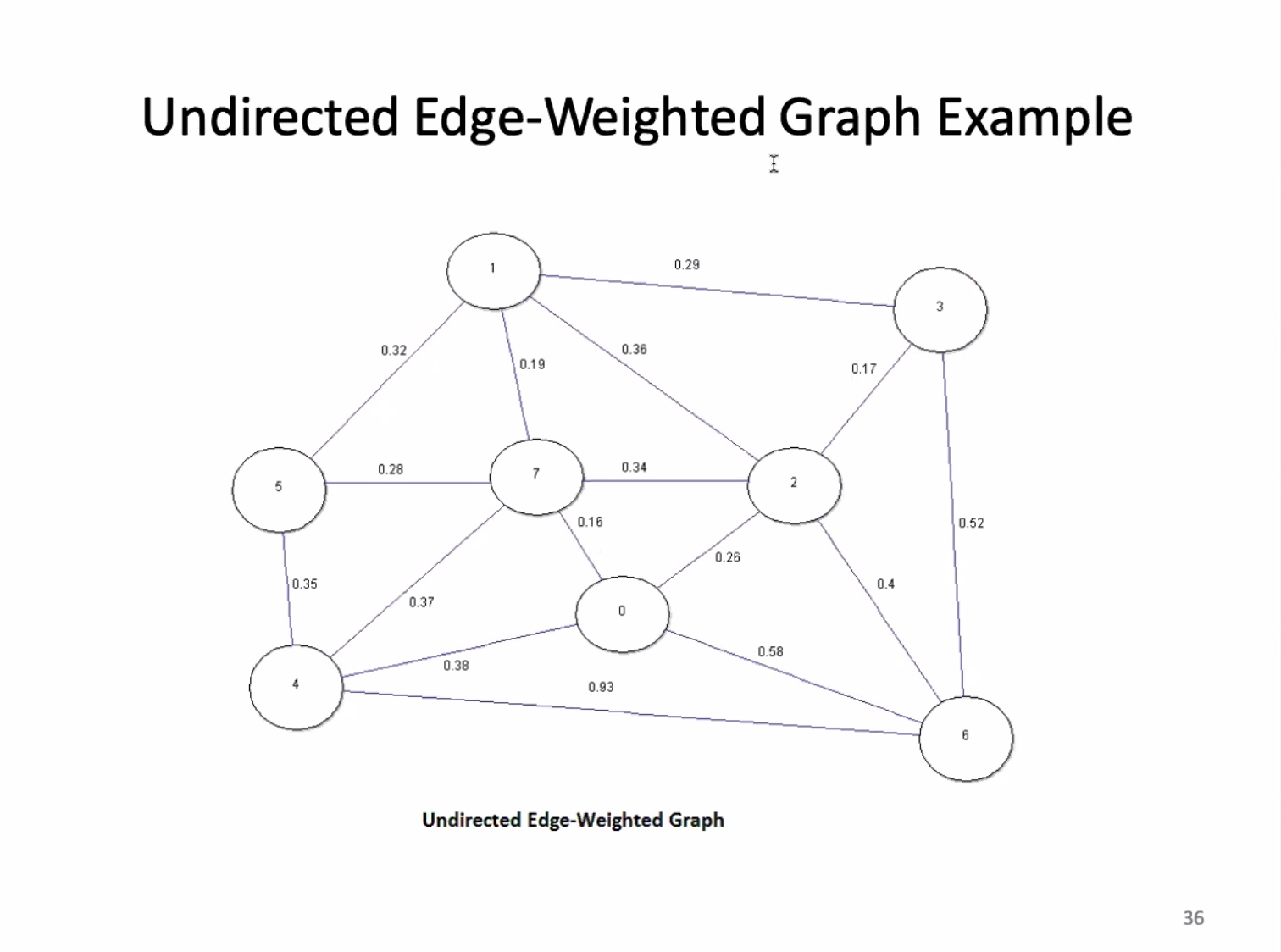
Weighted graphs #

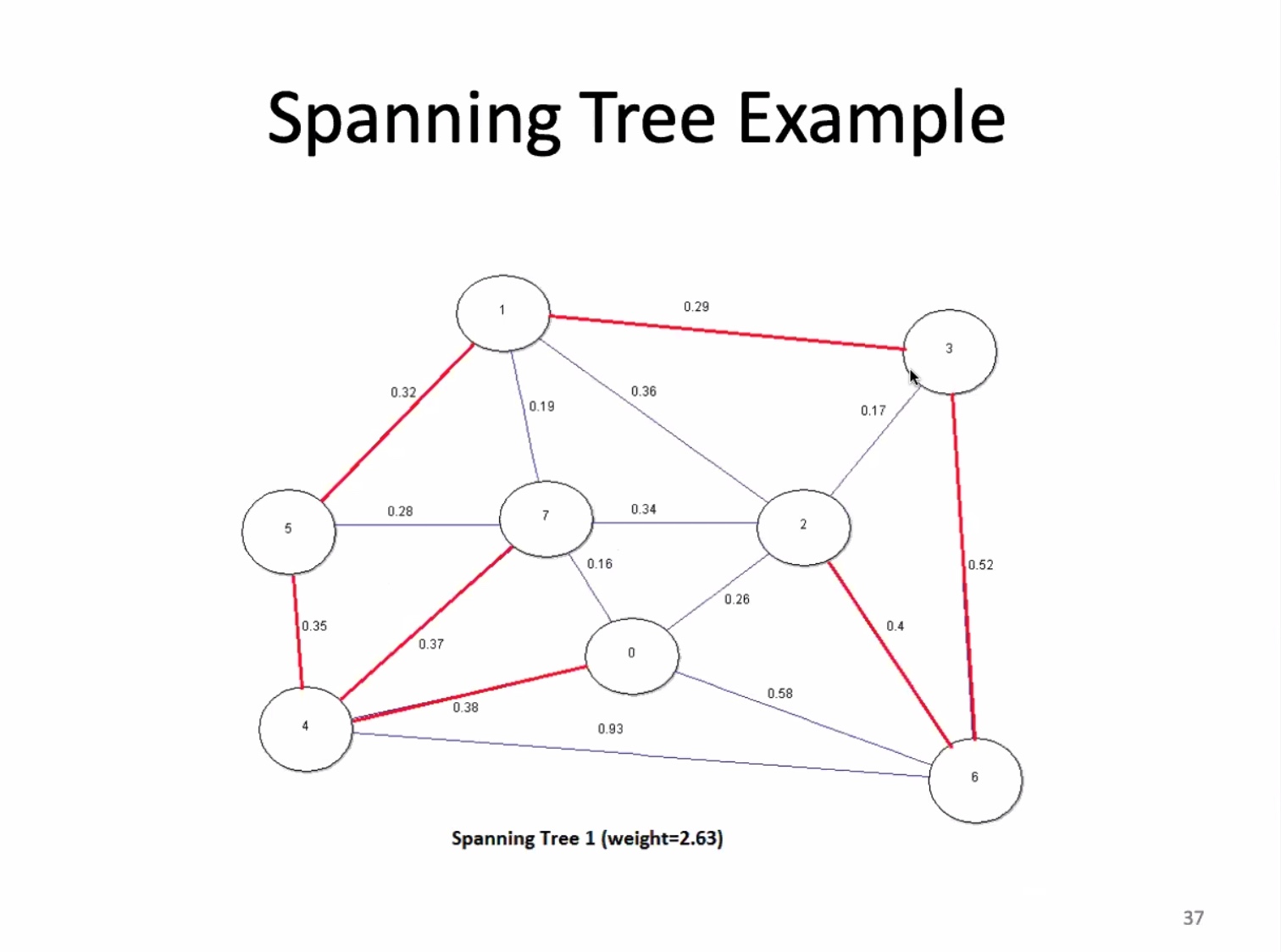
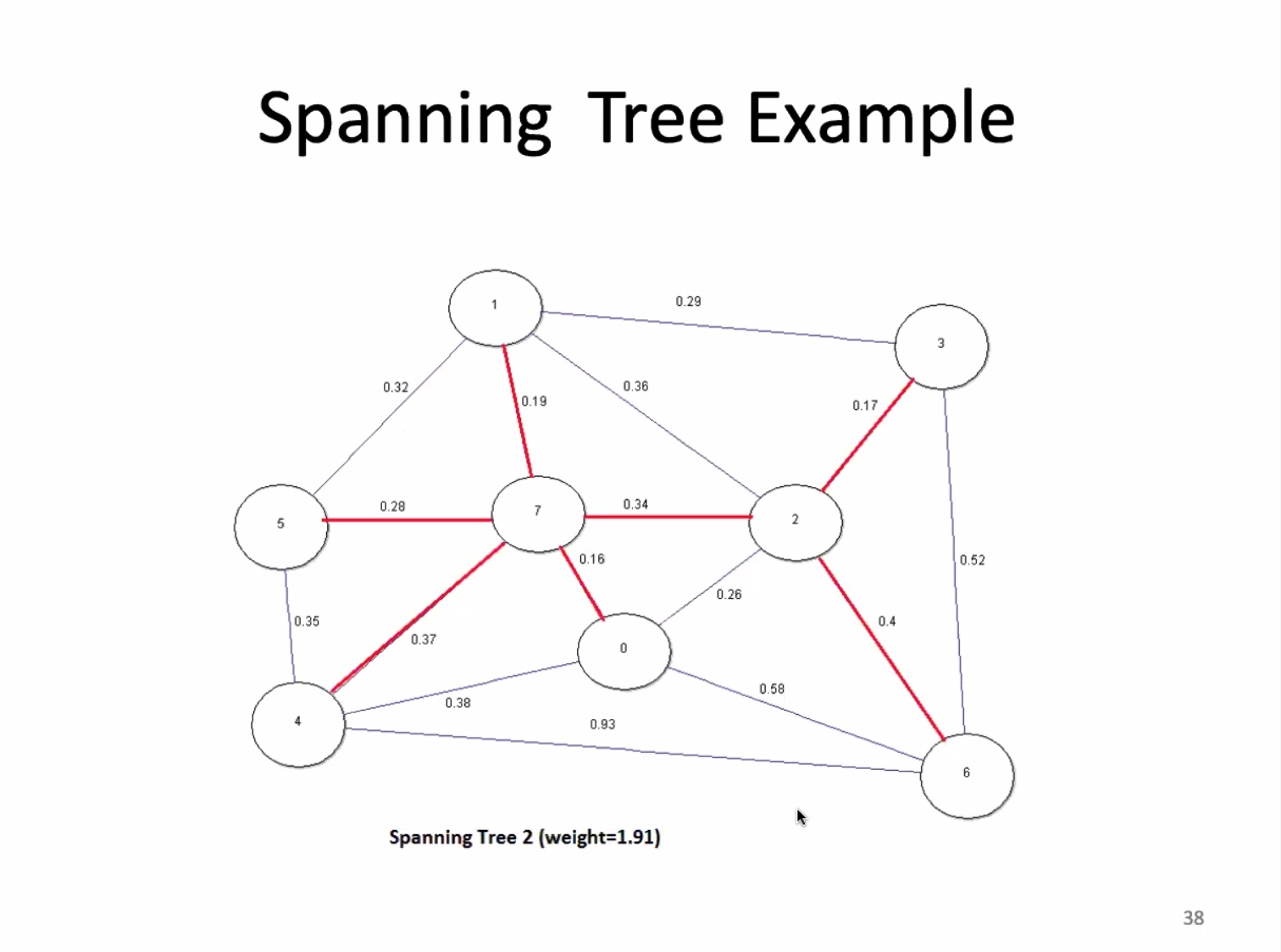
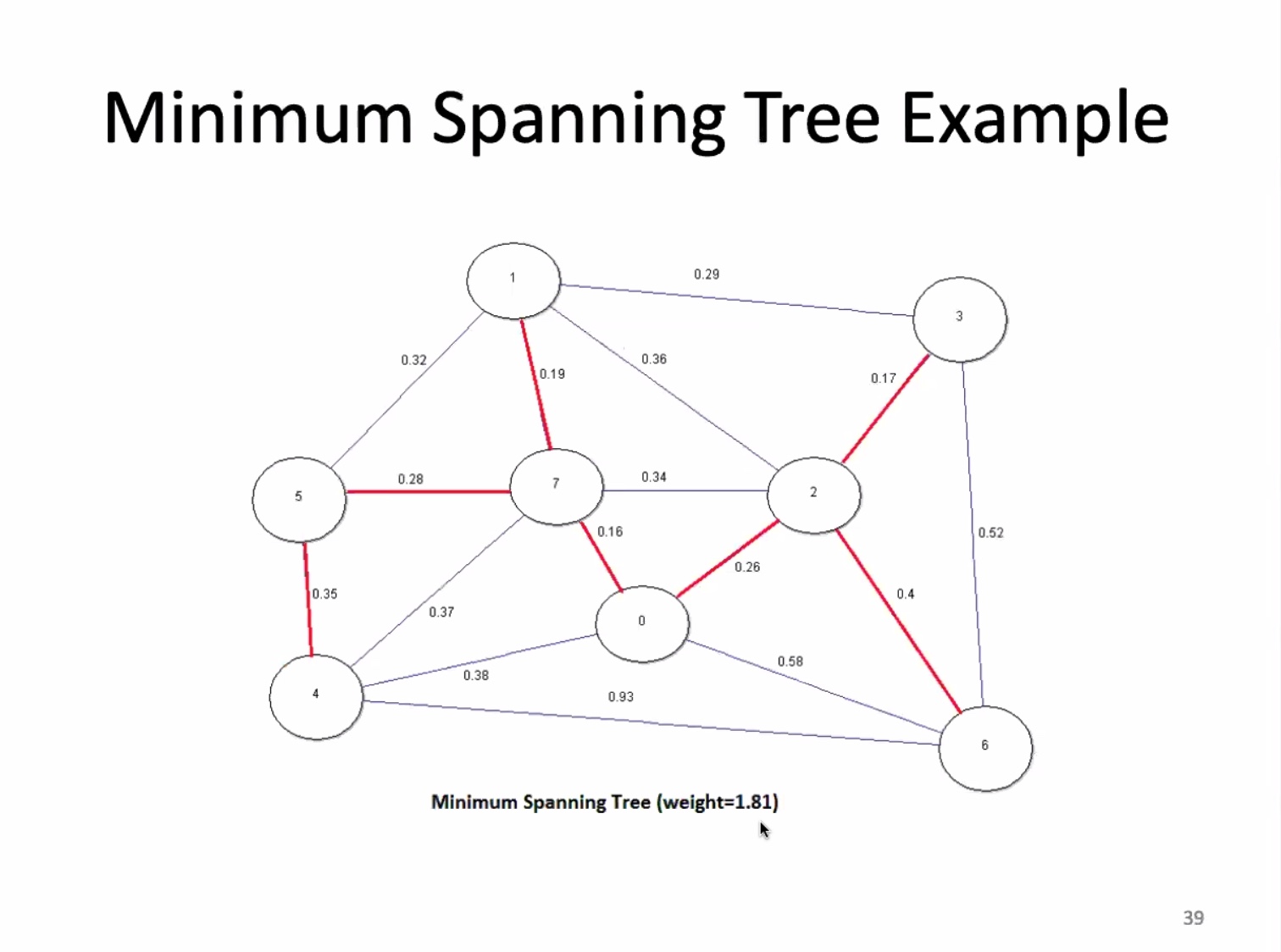
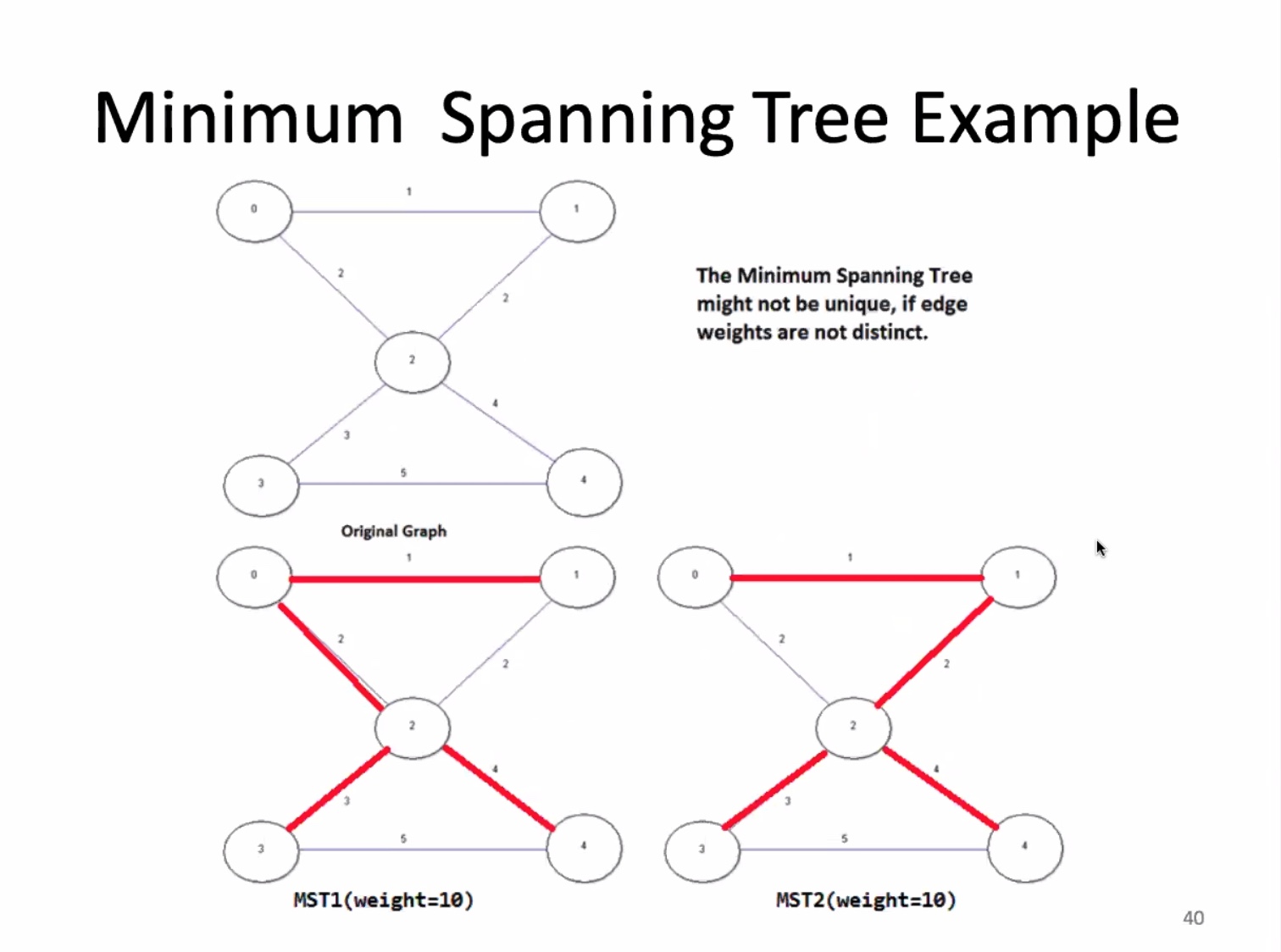
If a graph is not connected, it doesn’t have a spanning tree.

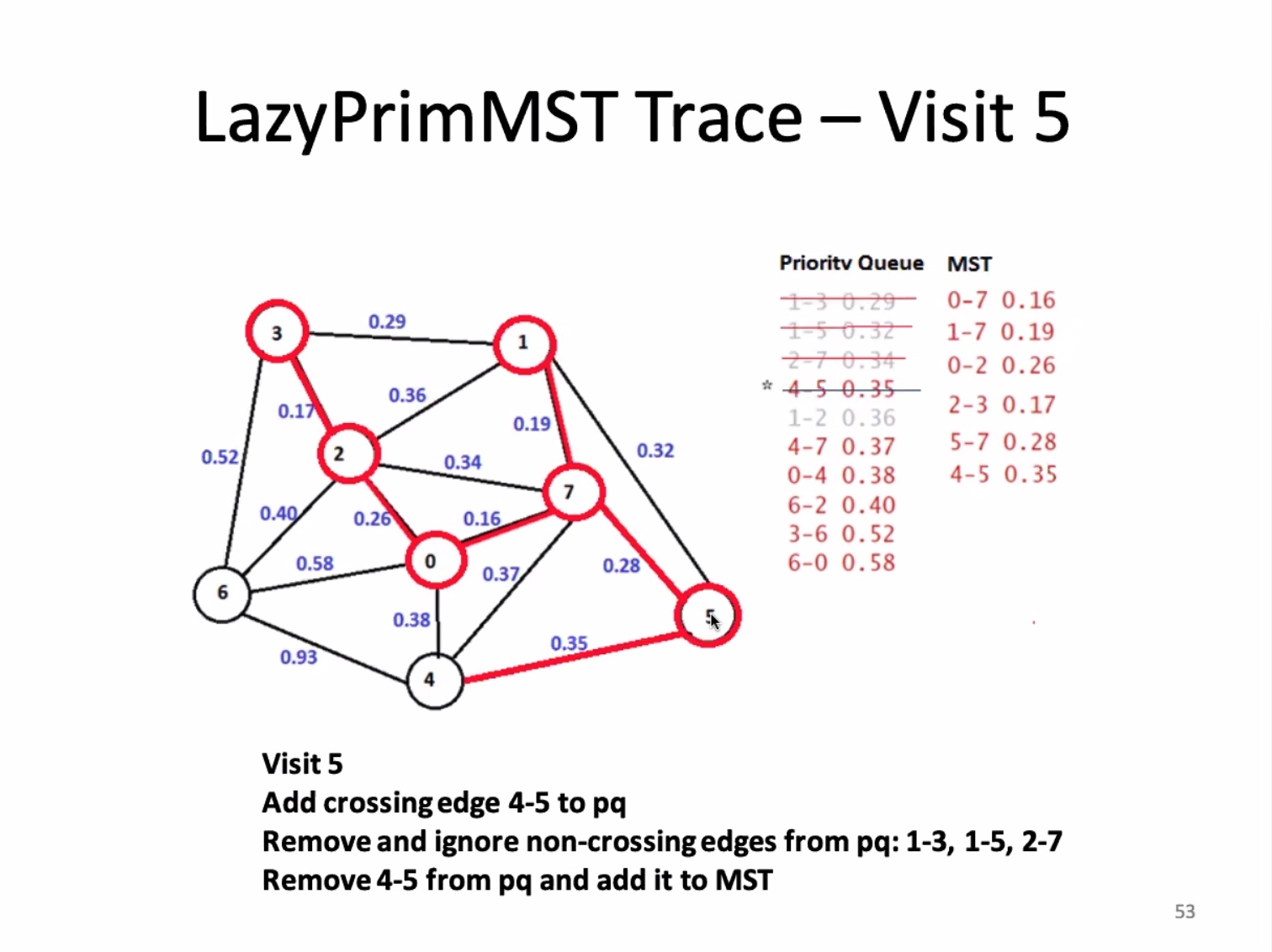
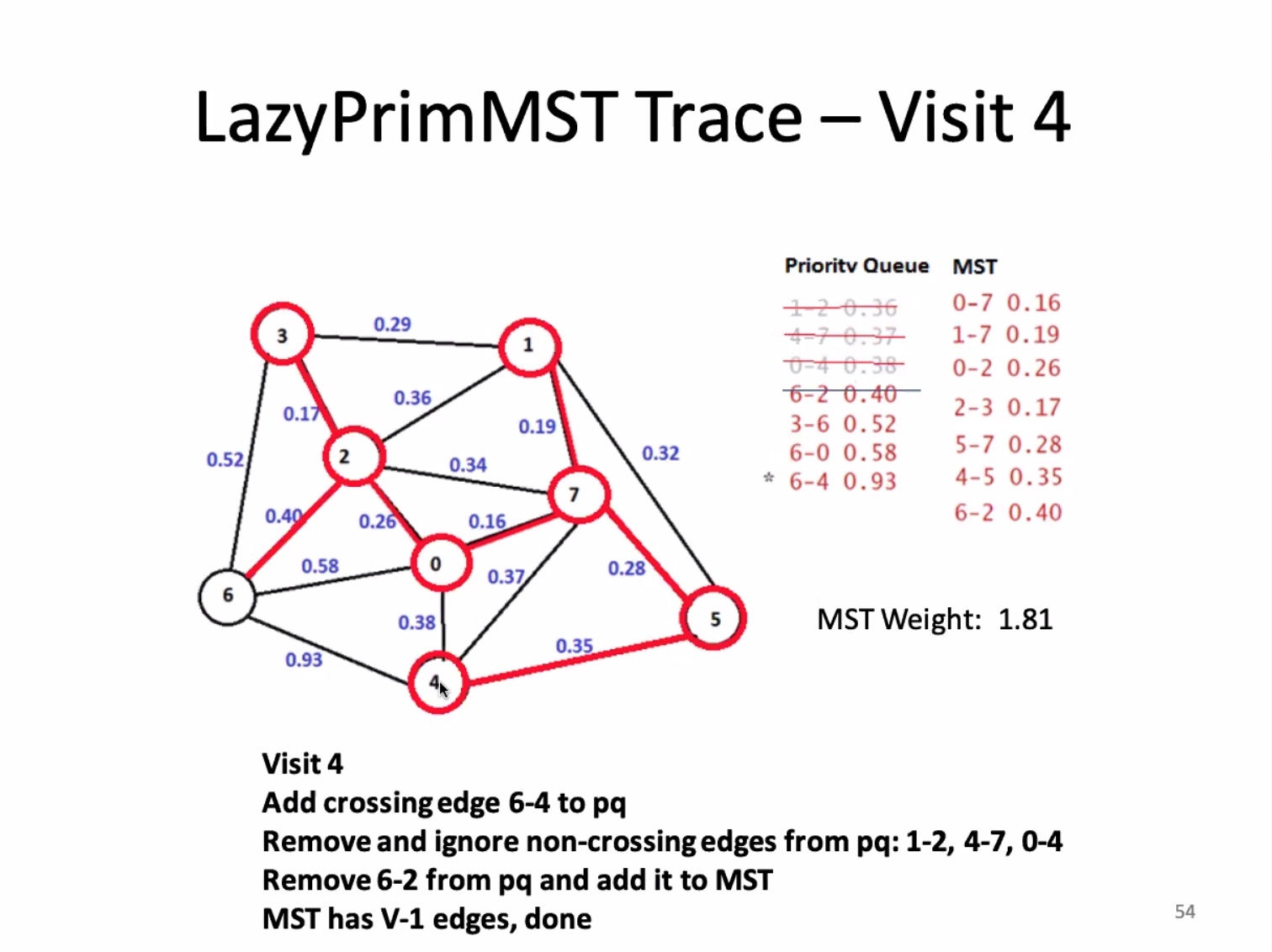
For an edge-weighted graph with (V) vertices, a MST has (V - 1) edges.

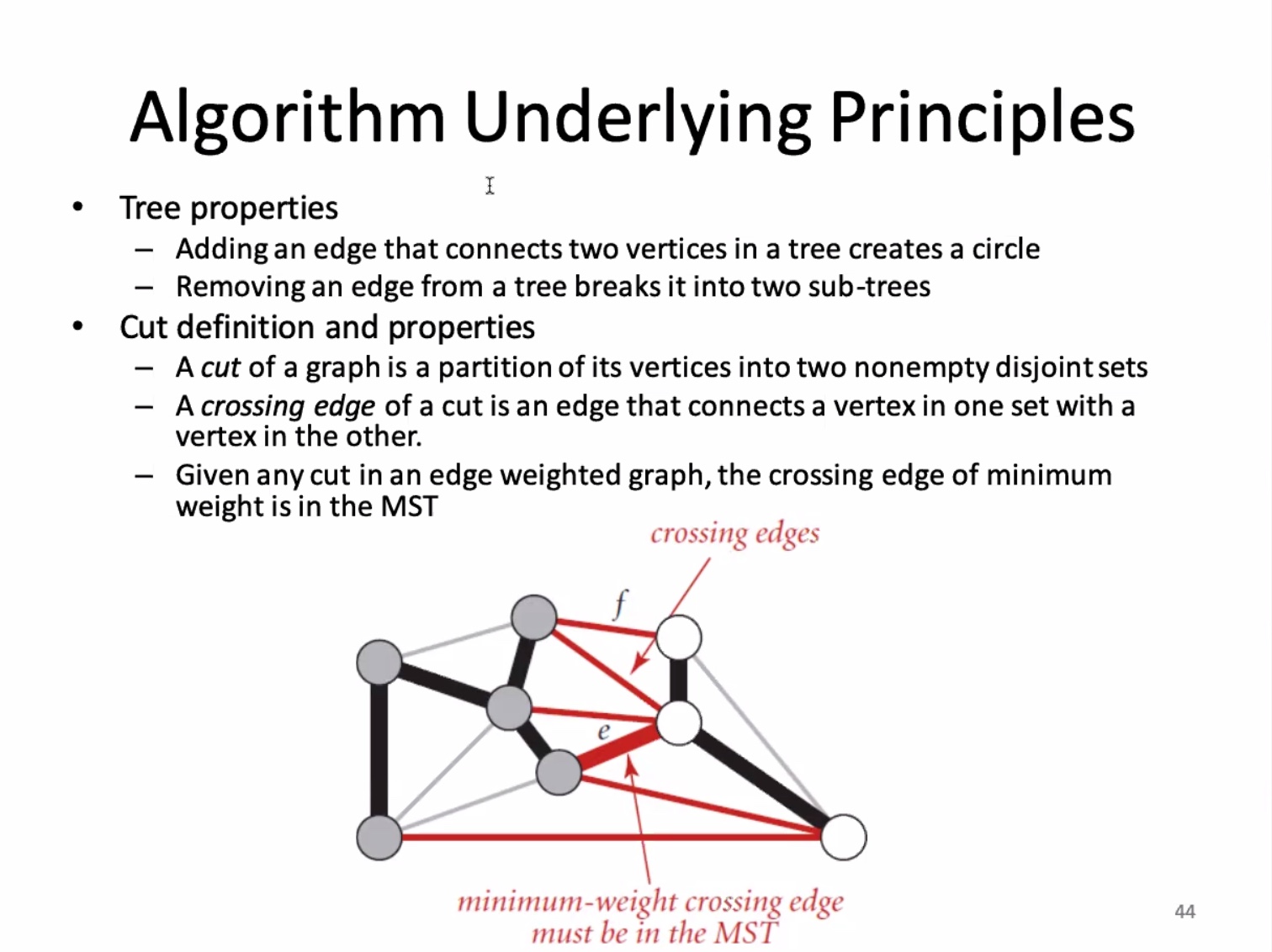
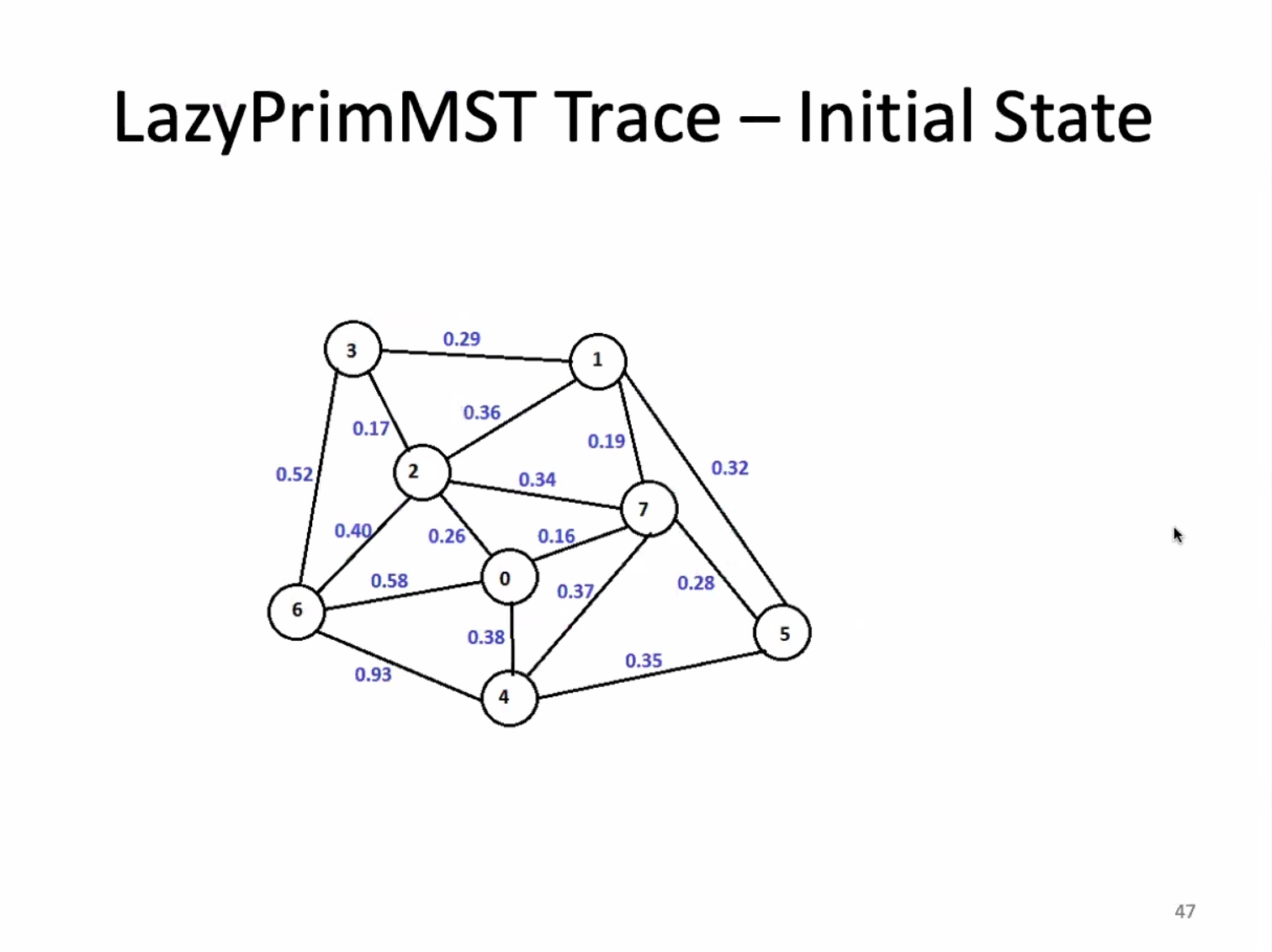
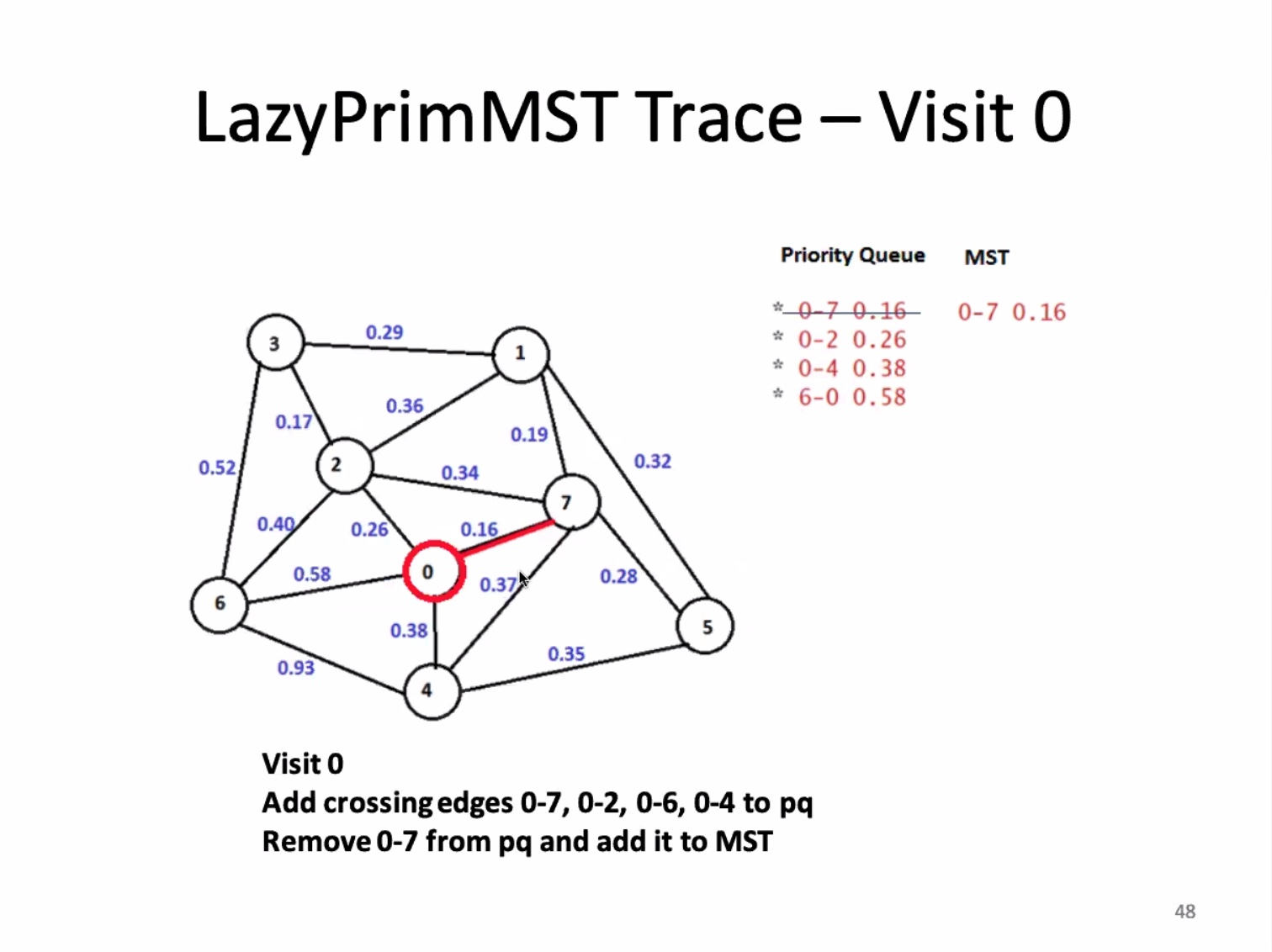
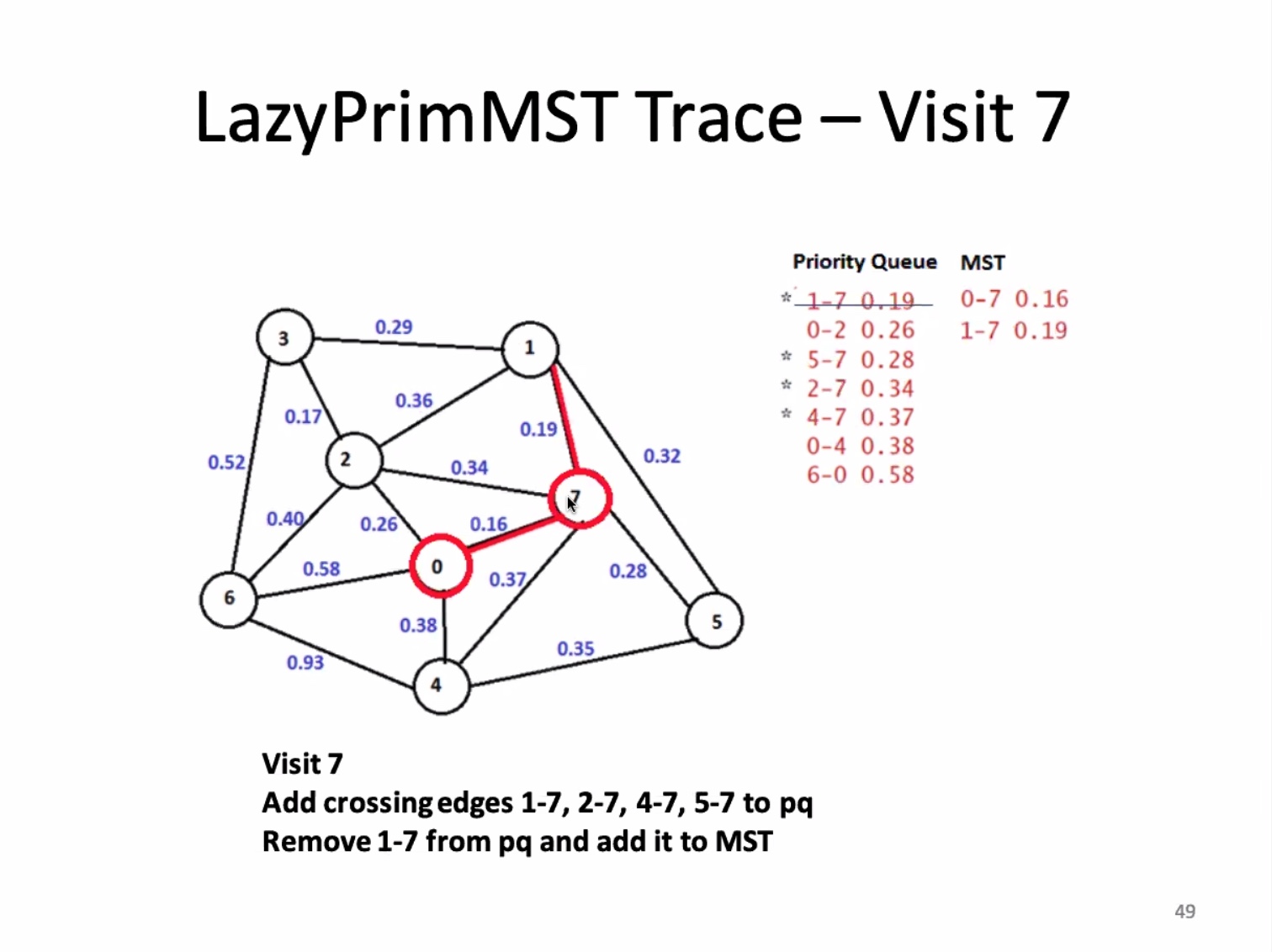
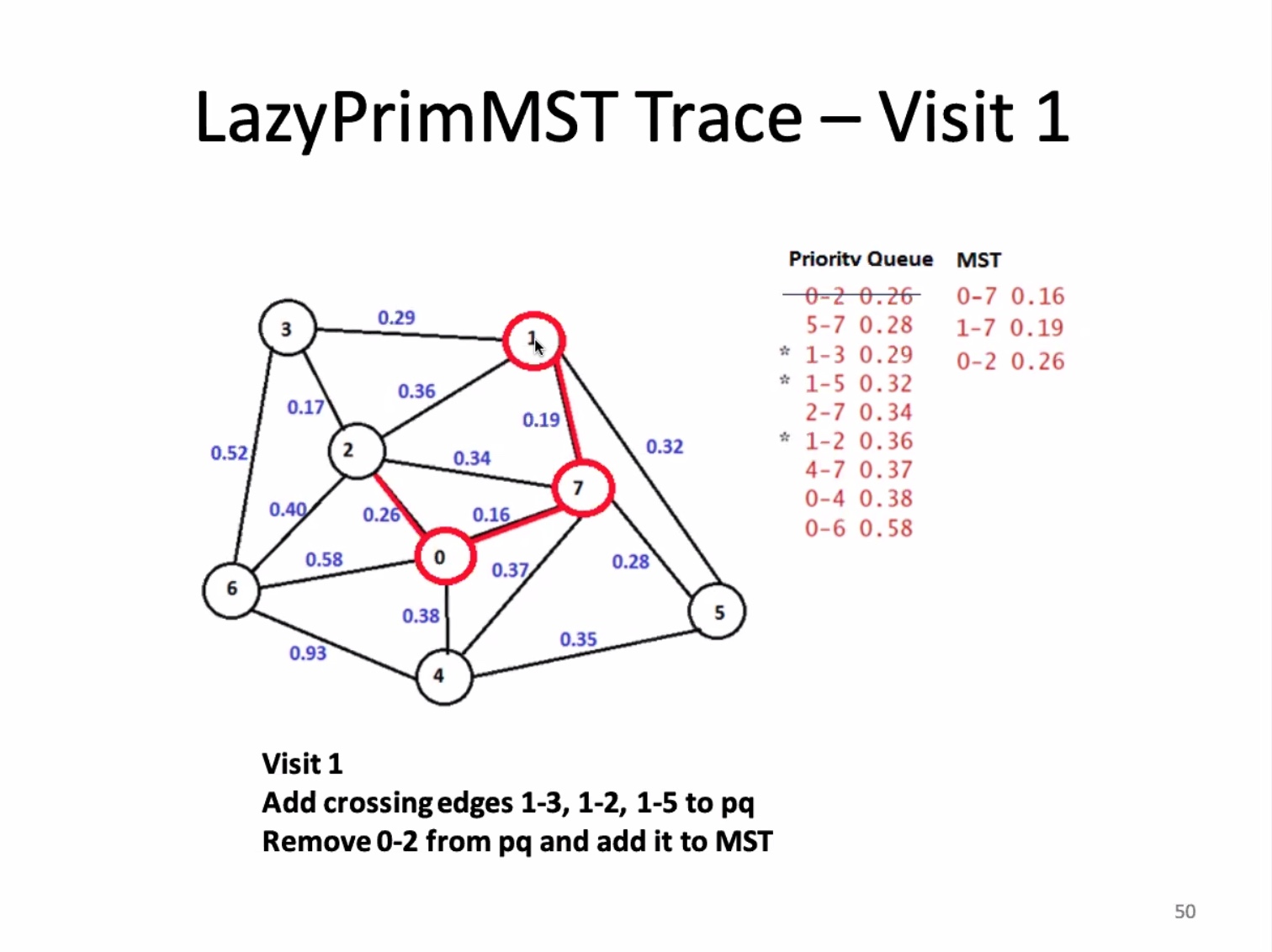
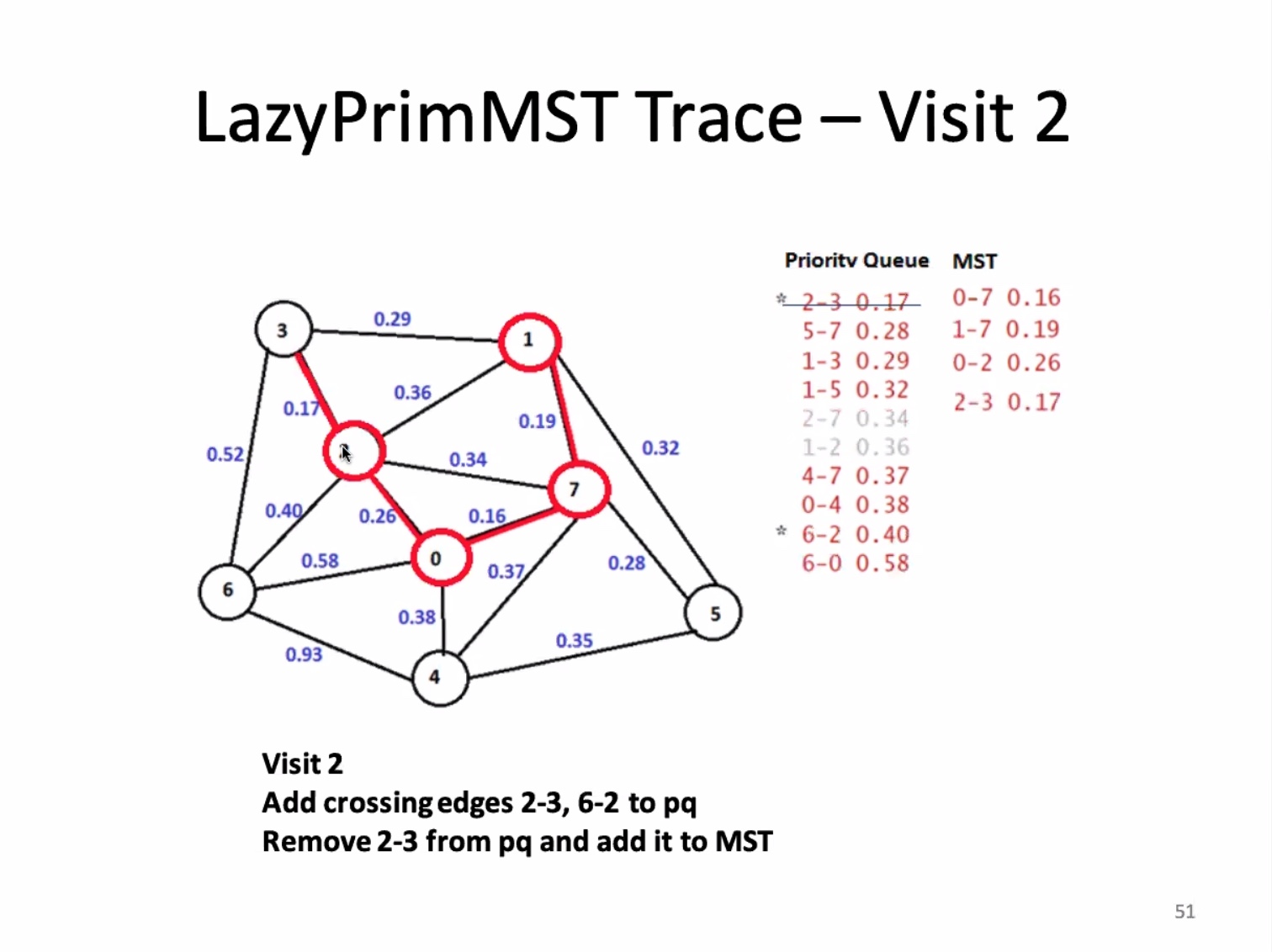
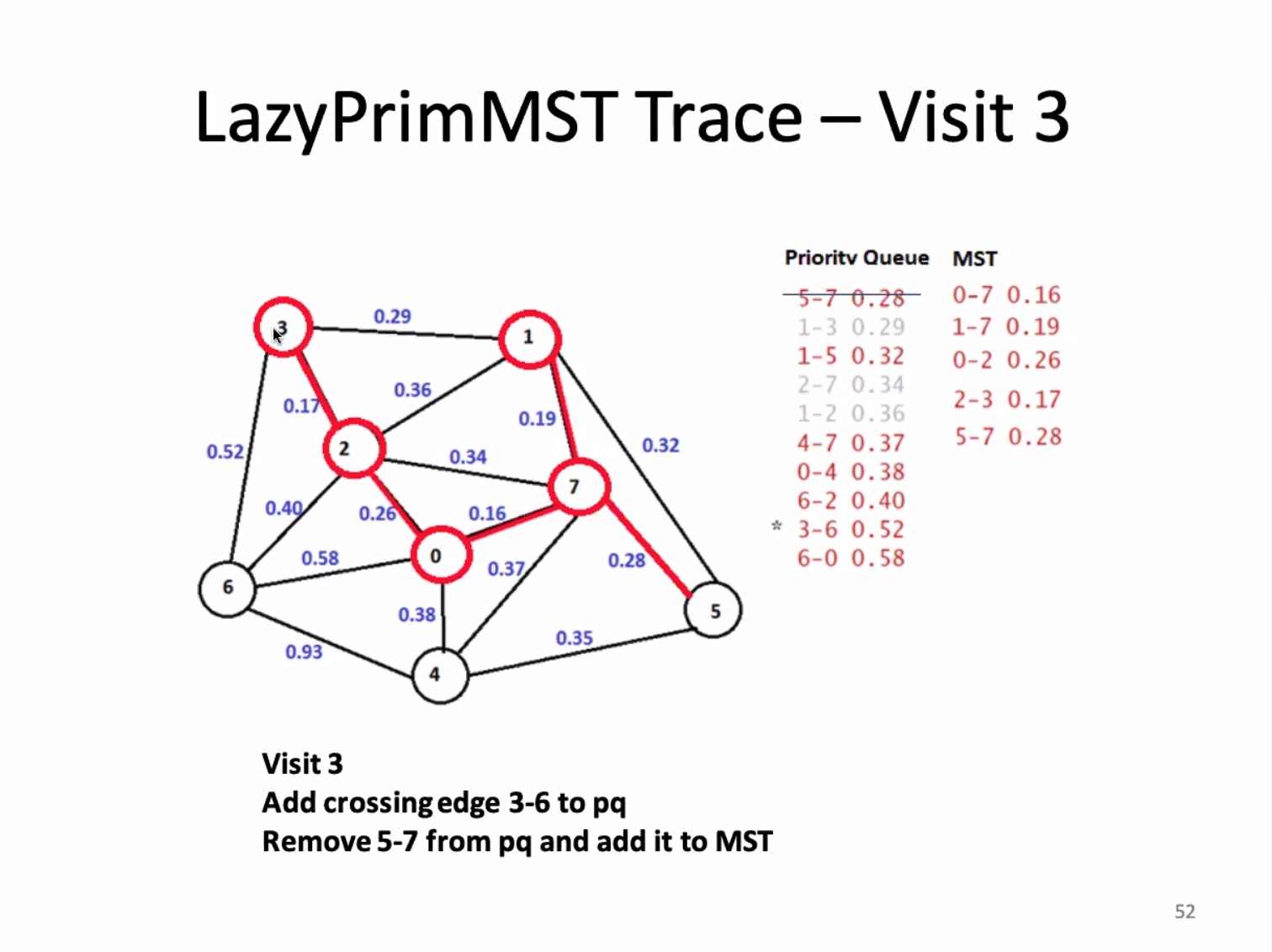
Another look at the implementation:

Worst case time comes from the pq operation.

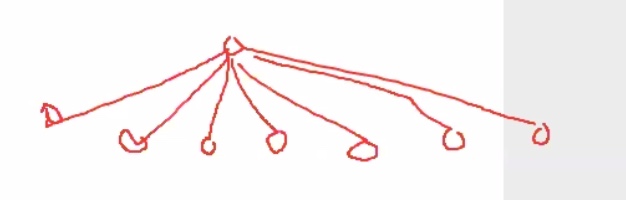
This type of graph gives the maximum size of the pq.

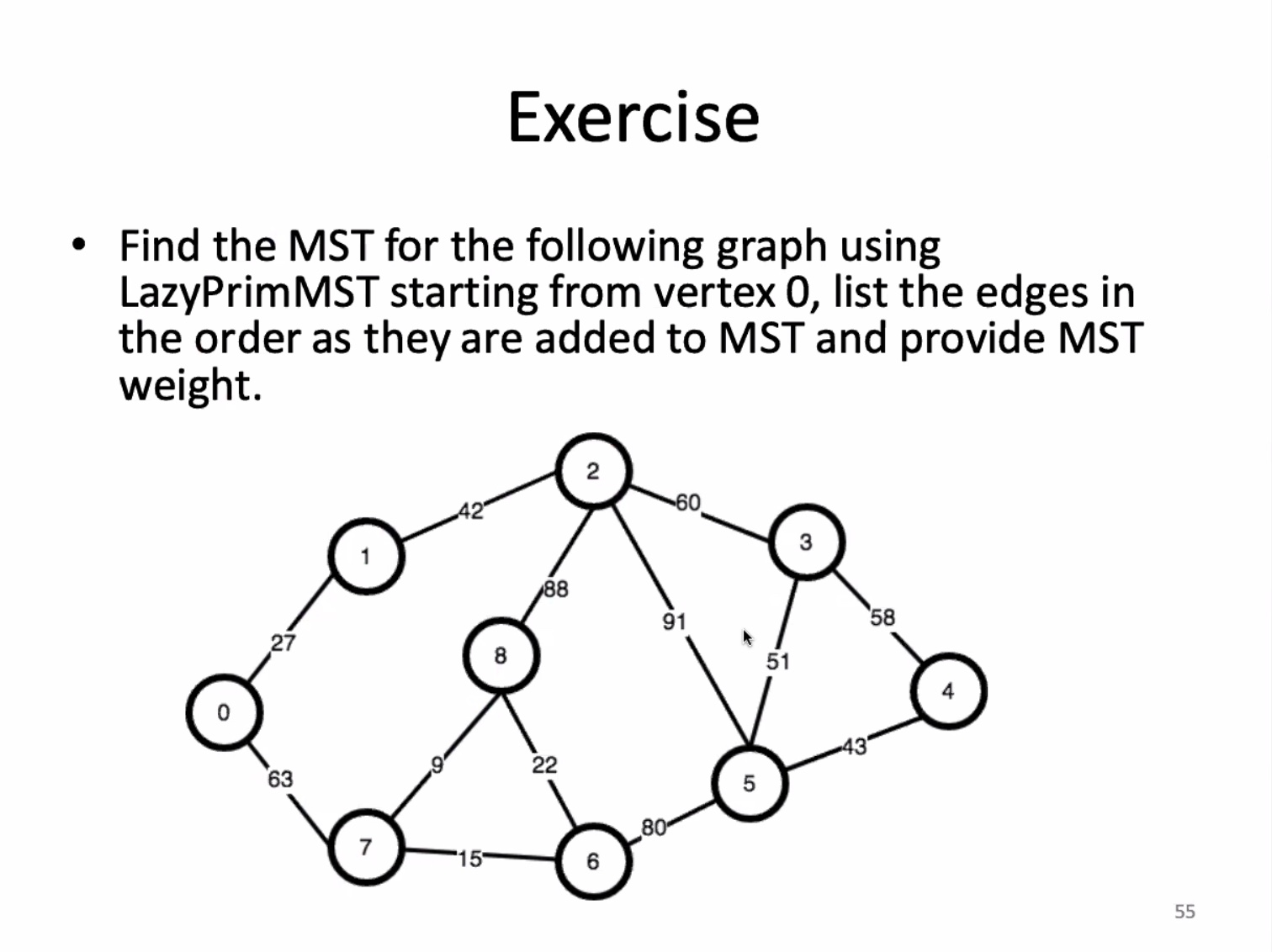
Skipping the eager prim implementation

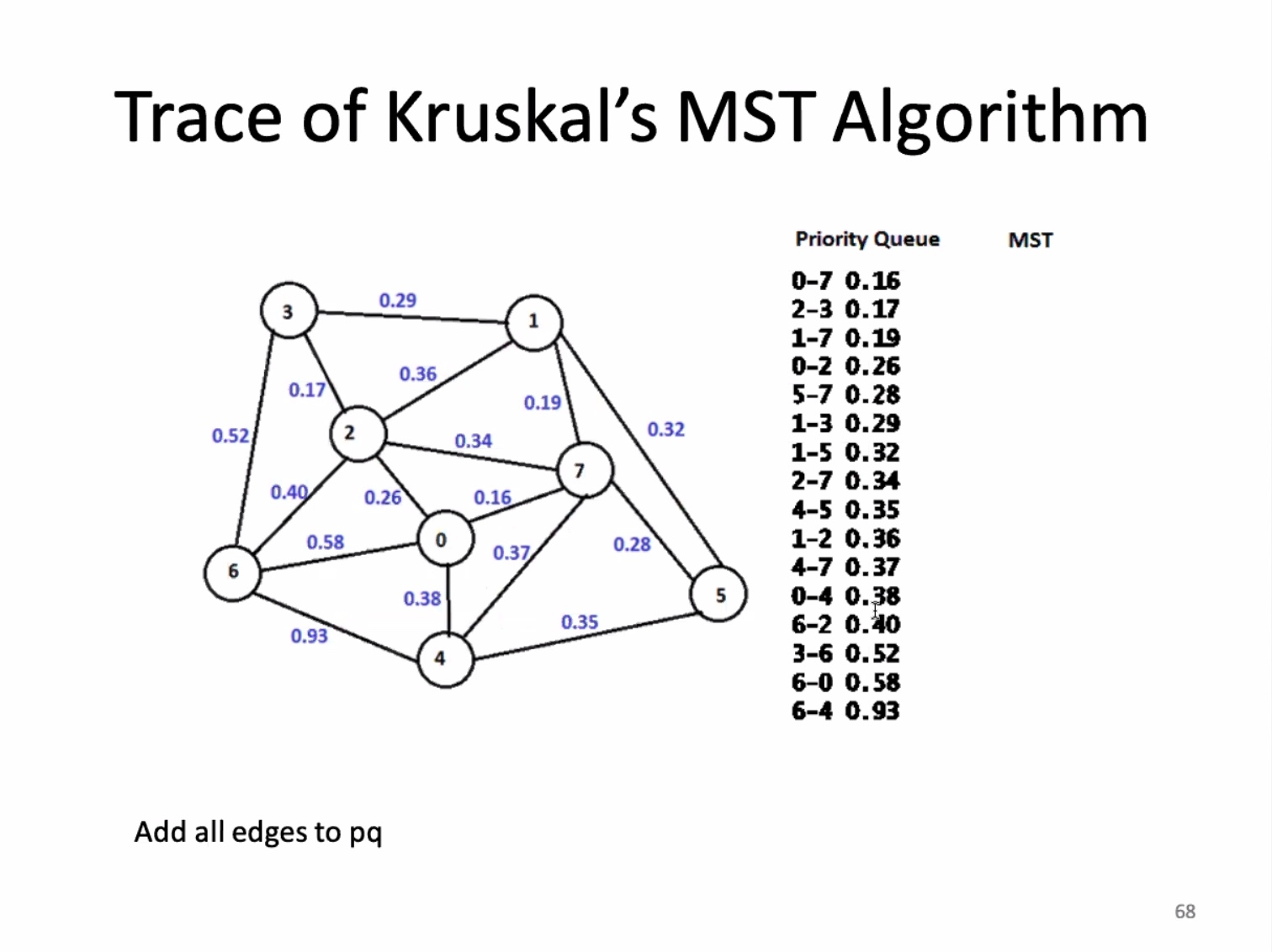
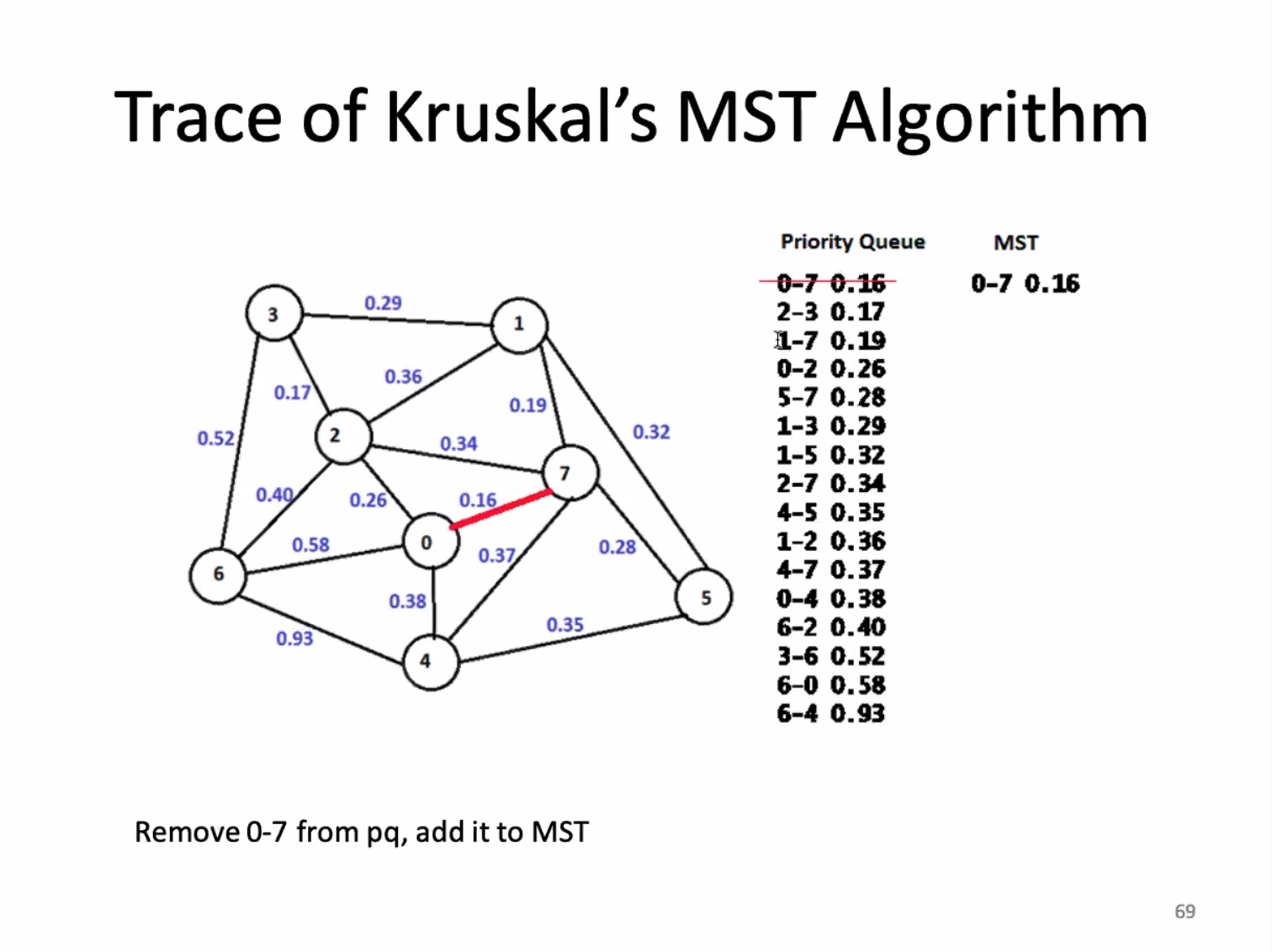
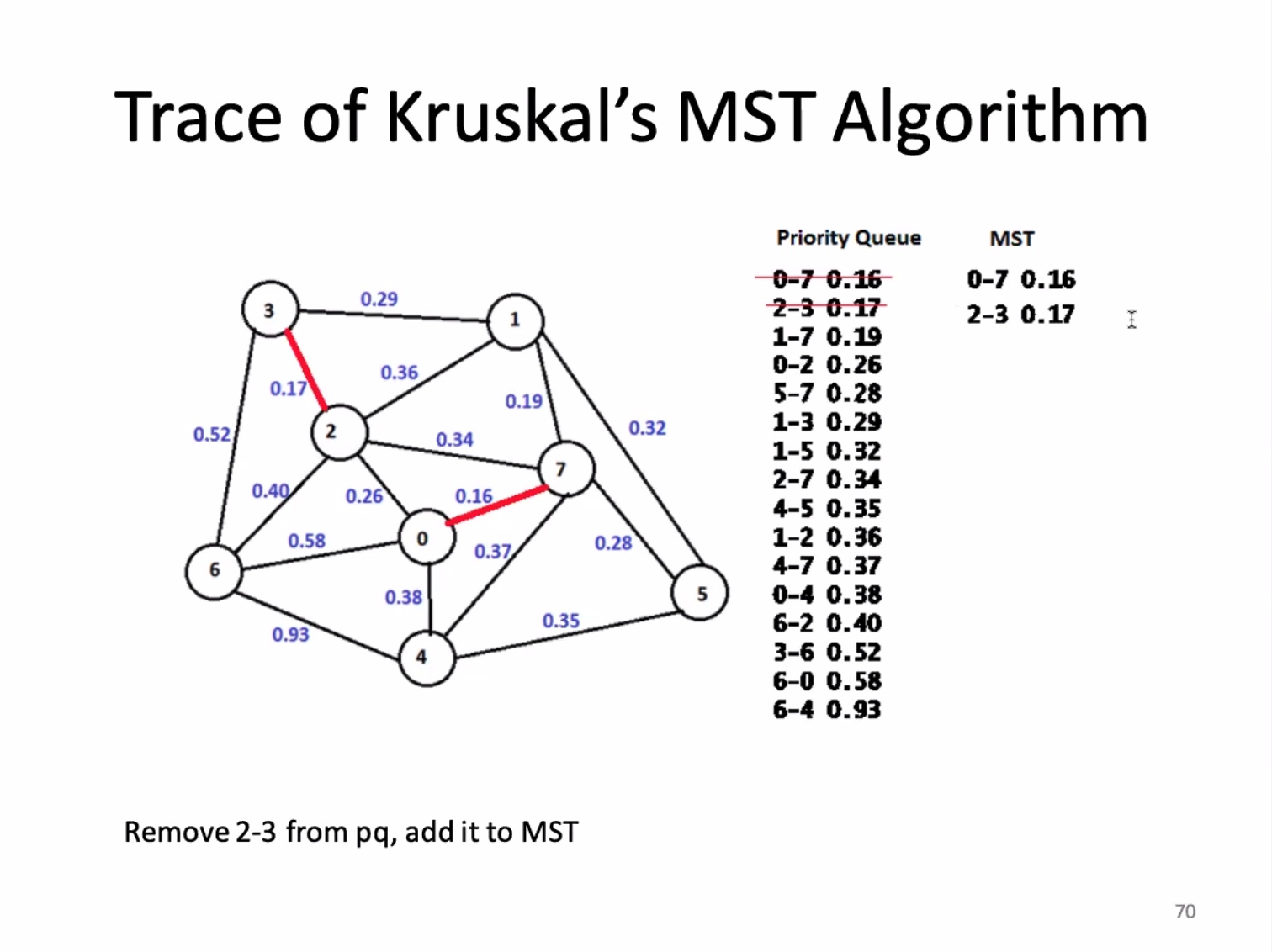
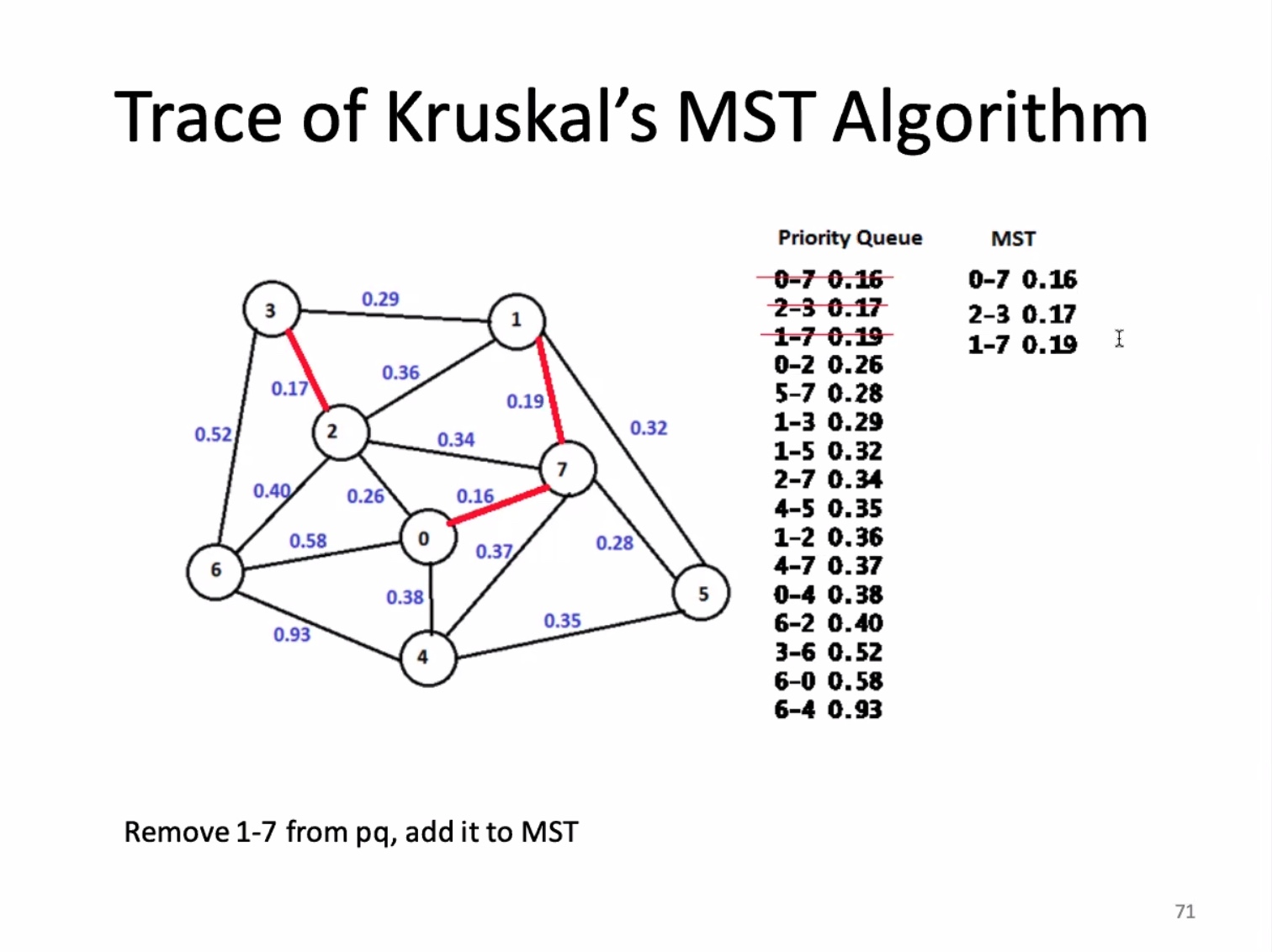
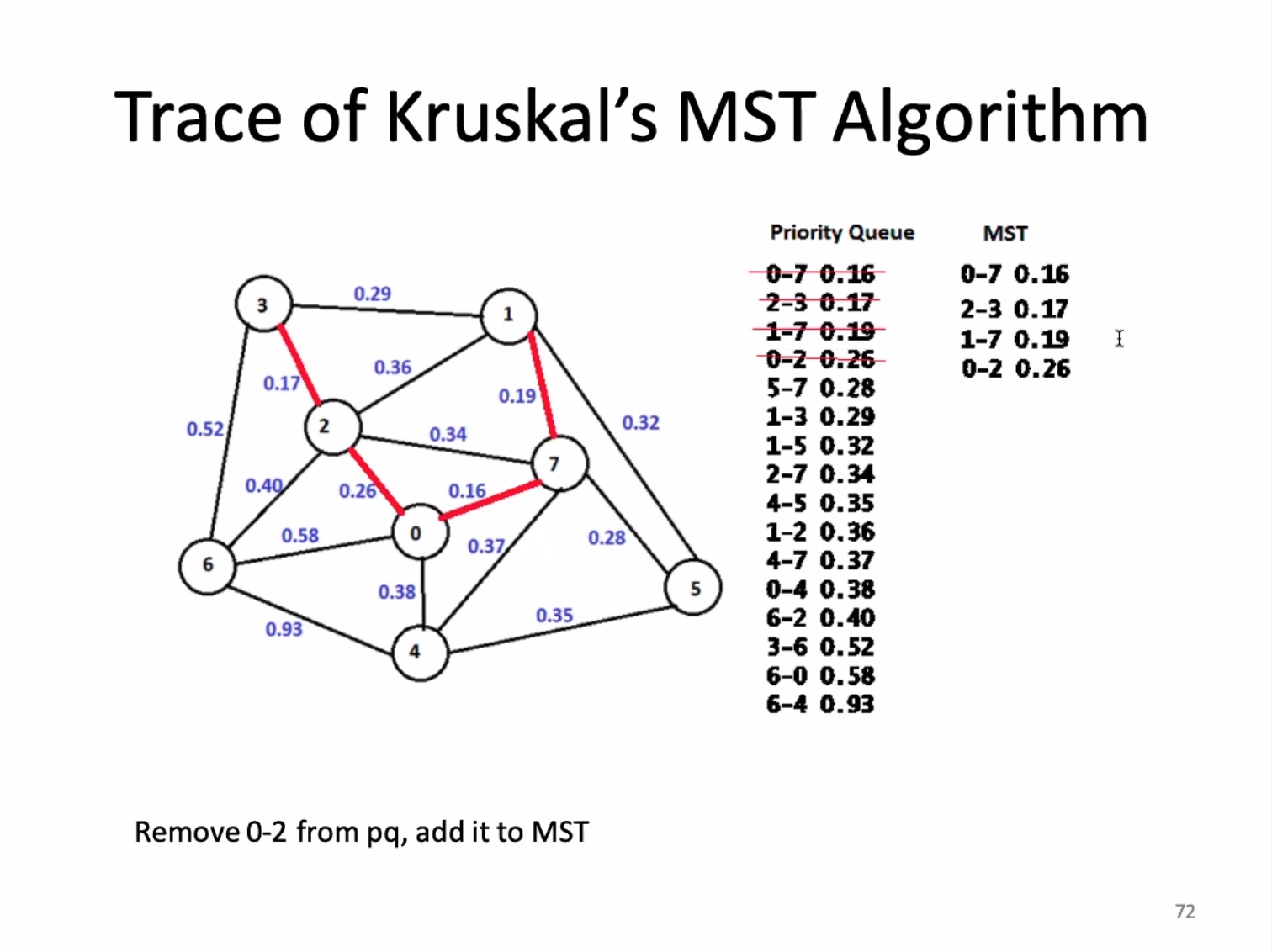
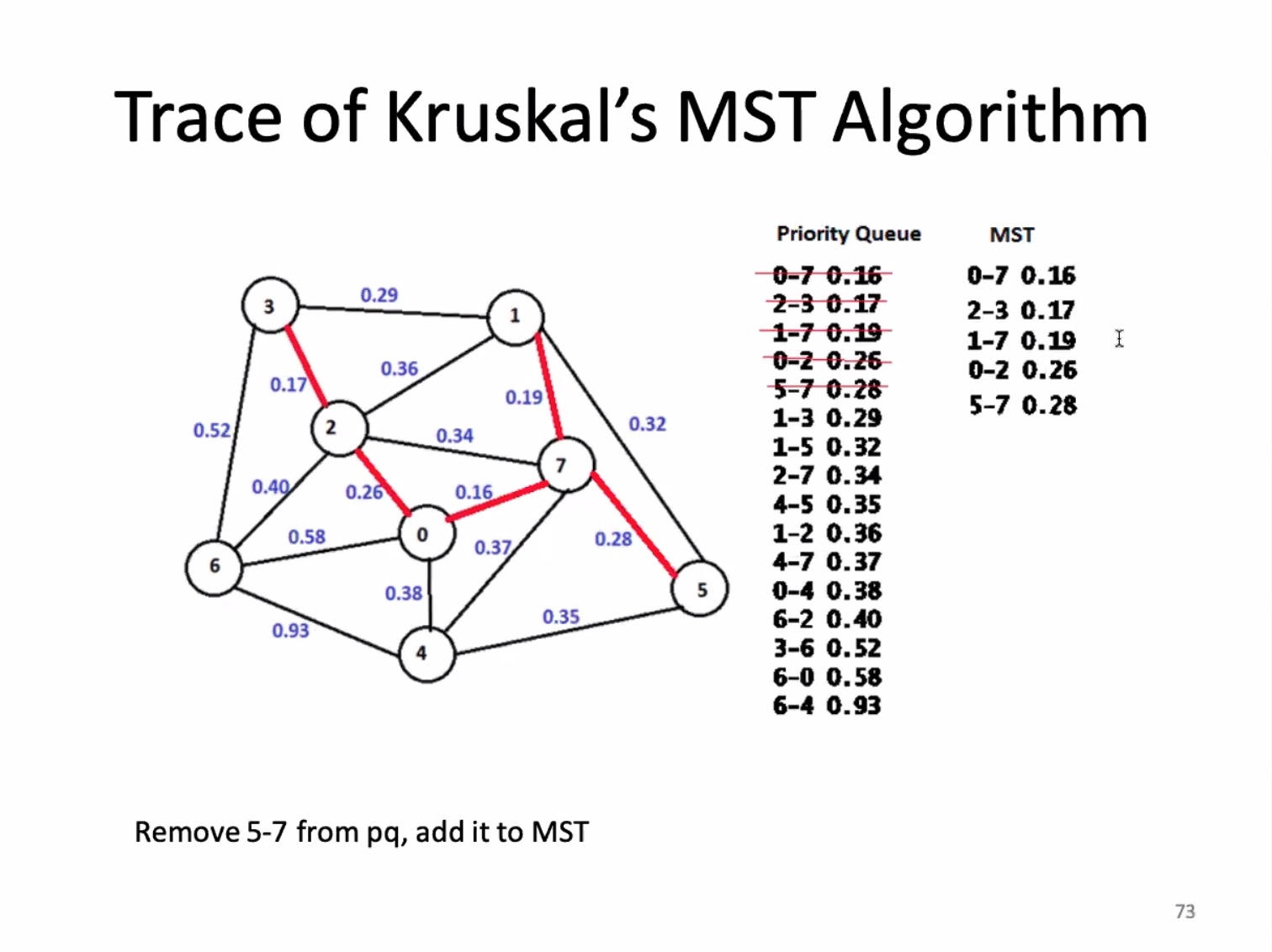
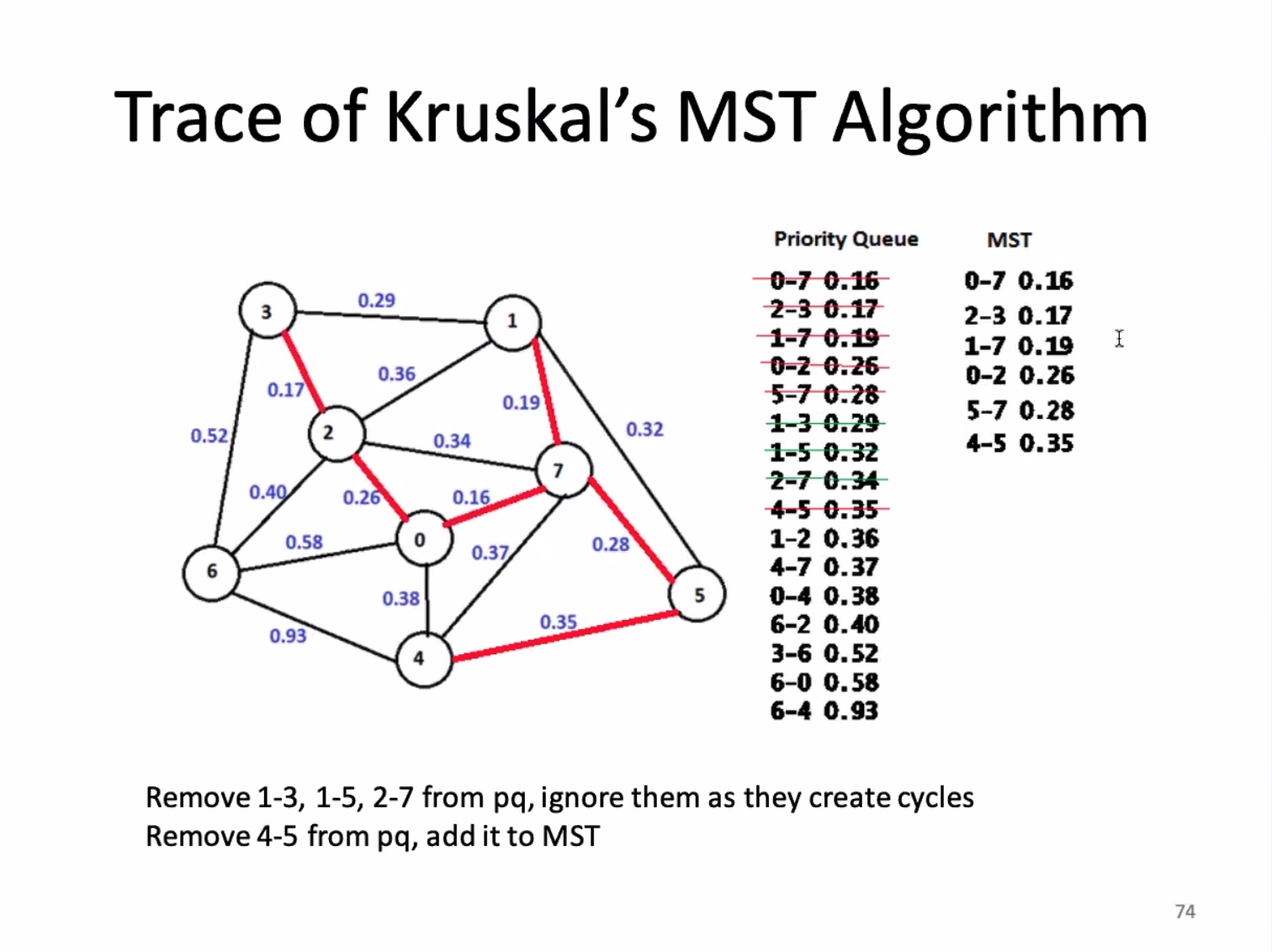
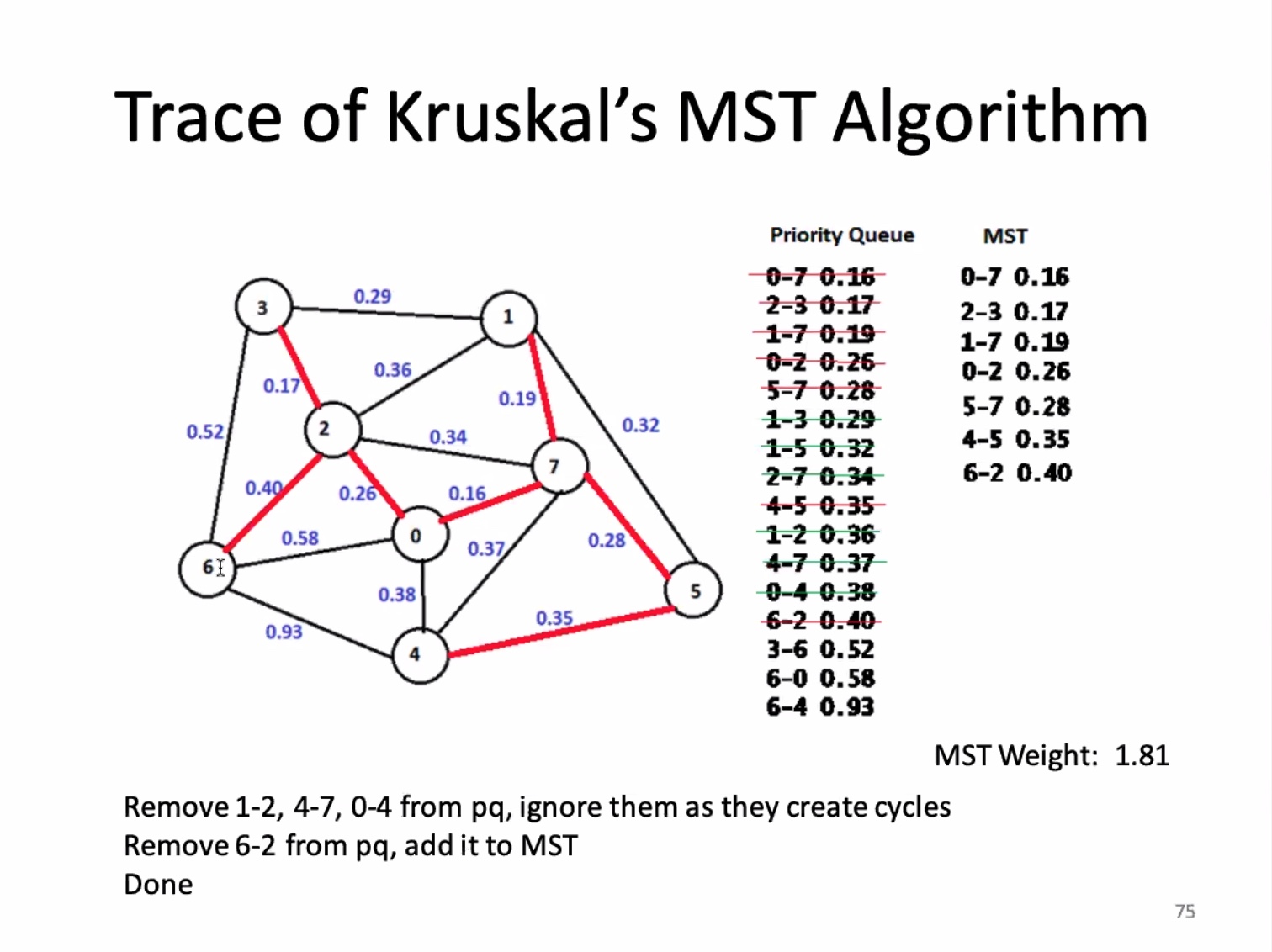
The for loop on 13 is O(ElgE). The union find is O(ElgV). and since E is greater than or equal to the vertices minus 1, the overall runtime is O(ElgE).

It won’t connect v and w because it will create a cycle.

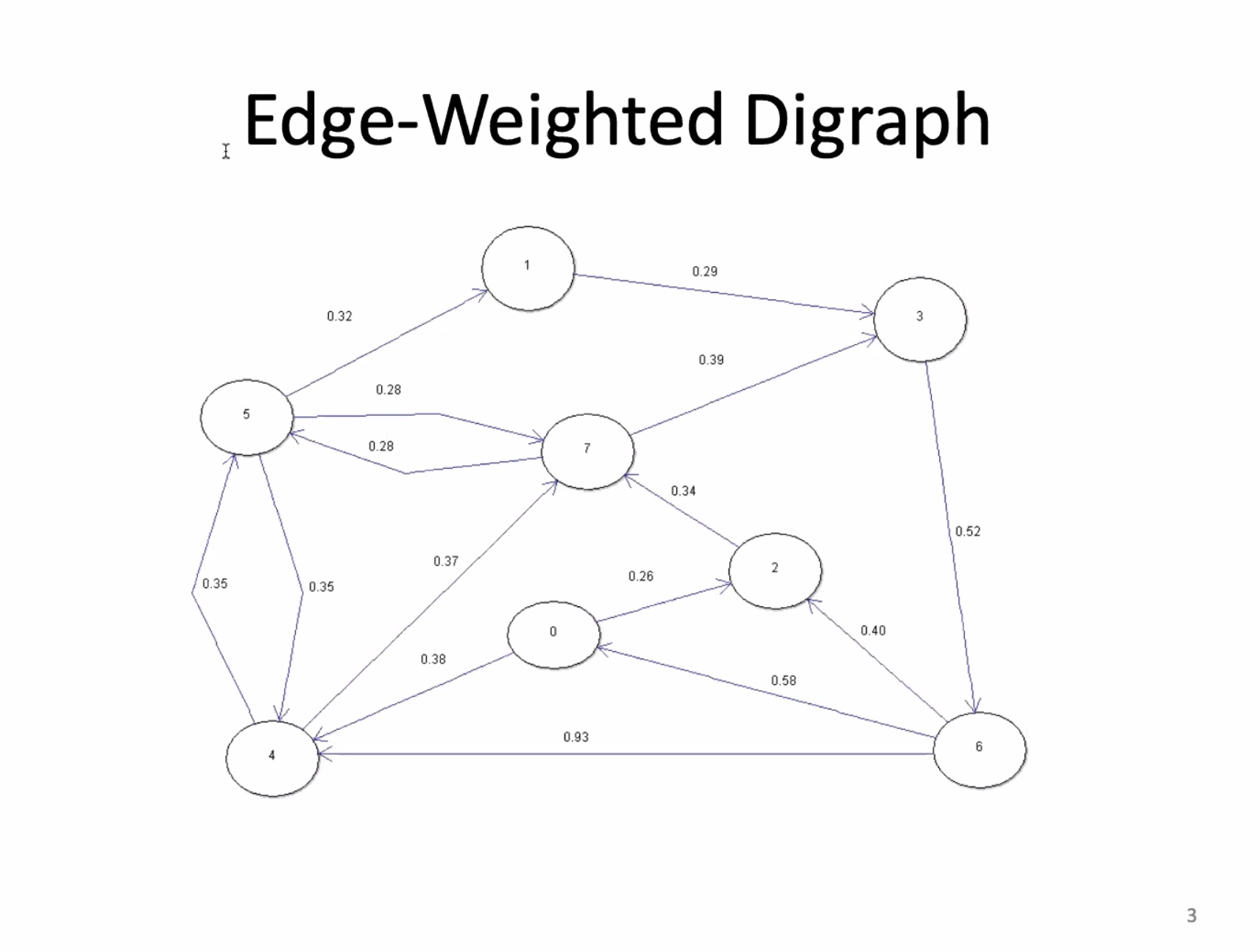
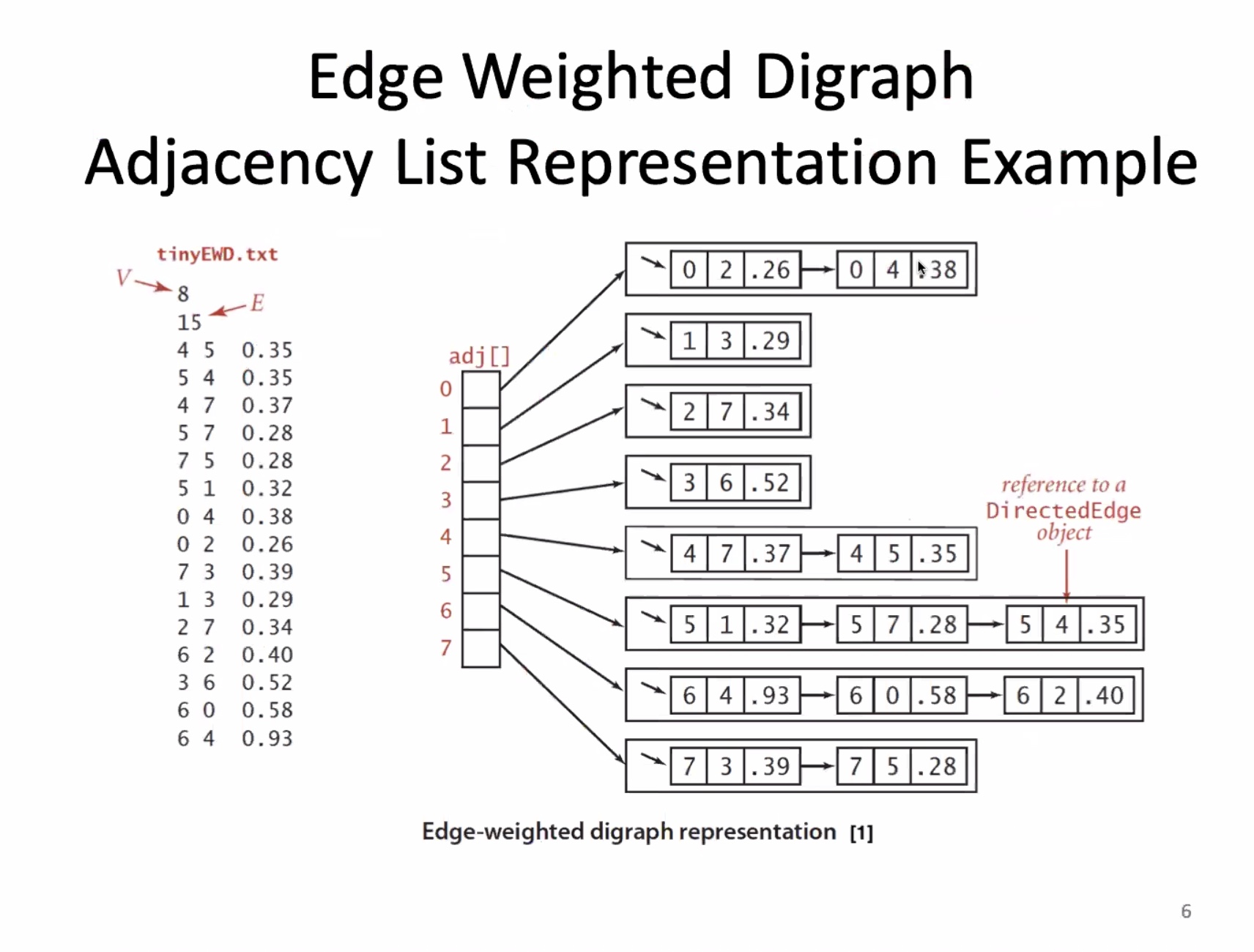
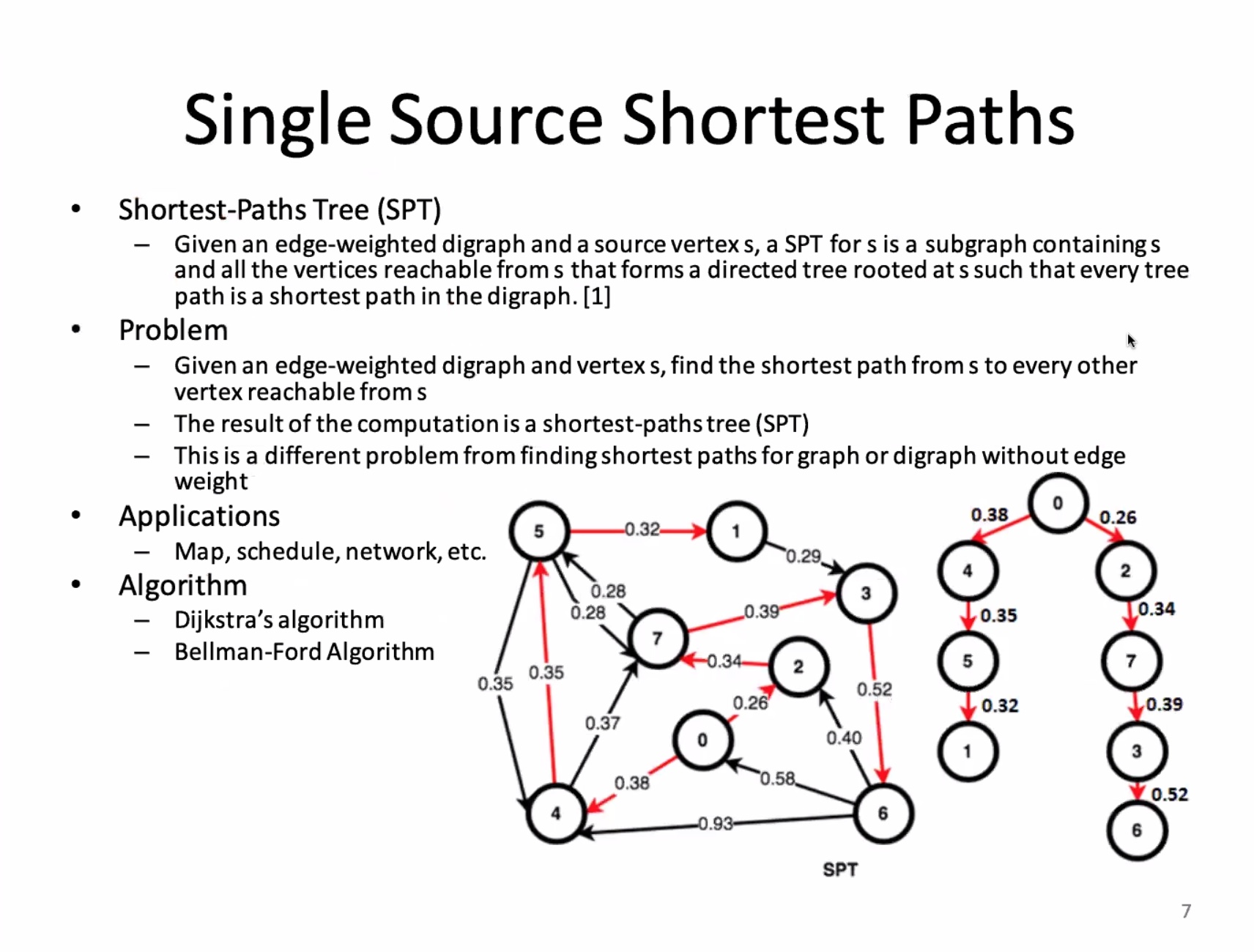
Edge weighted digraphs #