Exercise solns #

Graph cont. #

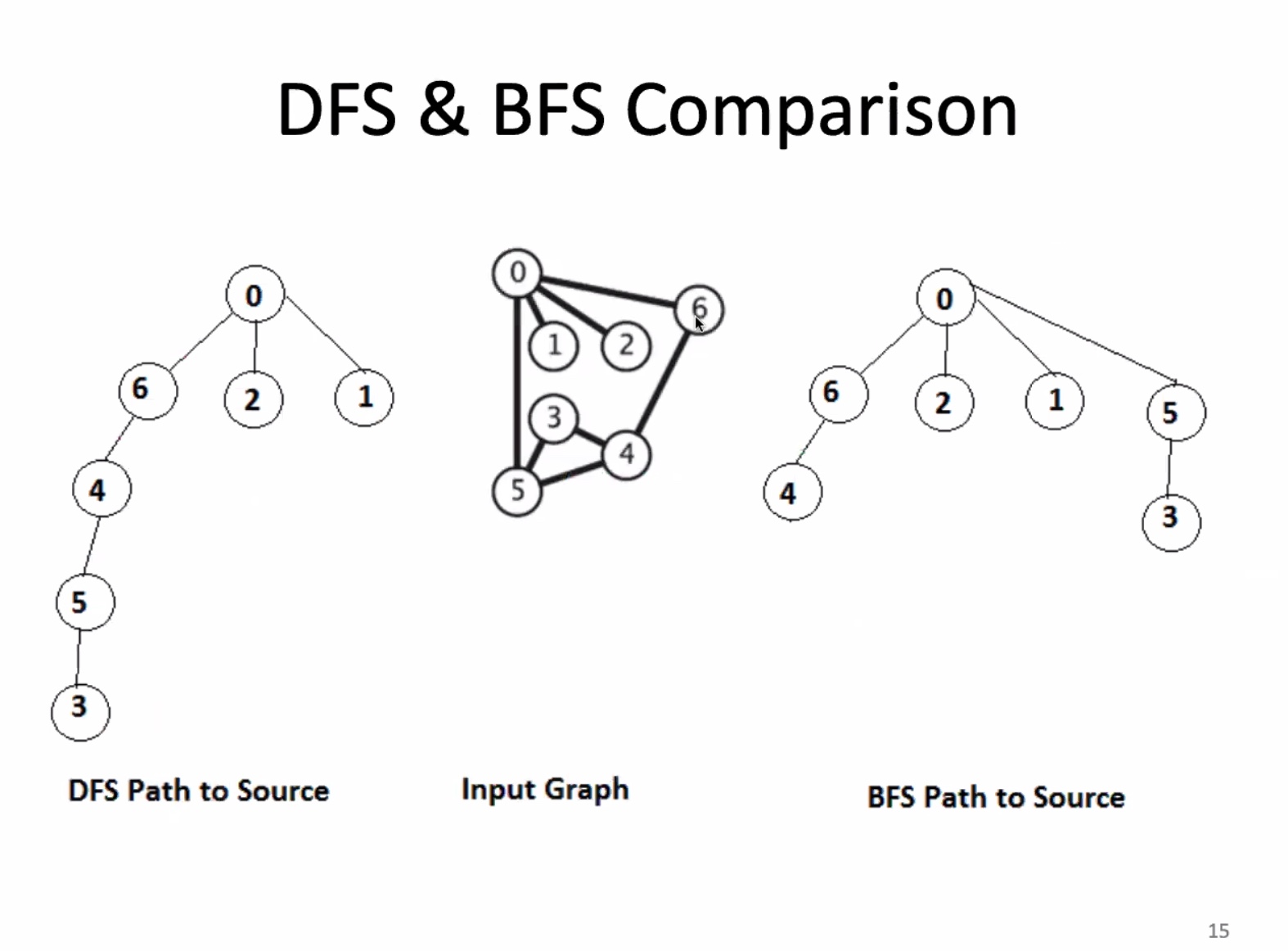
Gets shortest path because it starts by searching all edges that are 1 away, then 2 away, and so forth.

Tracing the BFS implementation

Enter the loop

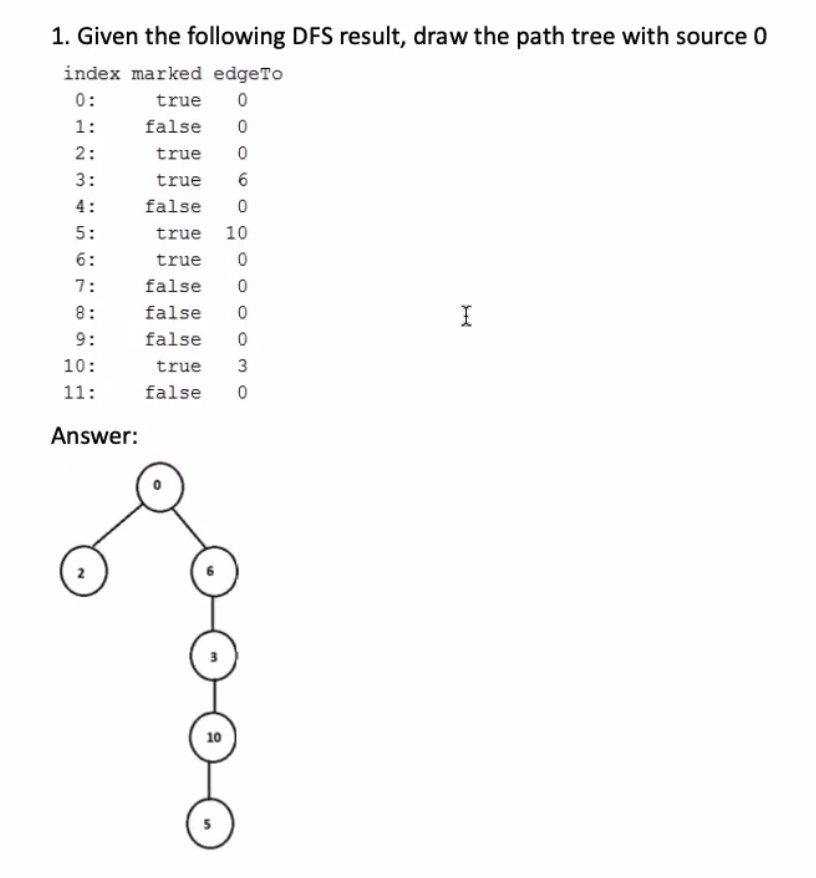
Path tree on right ^

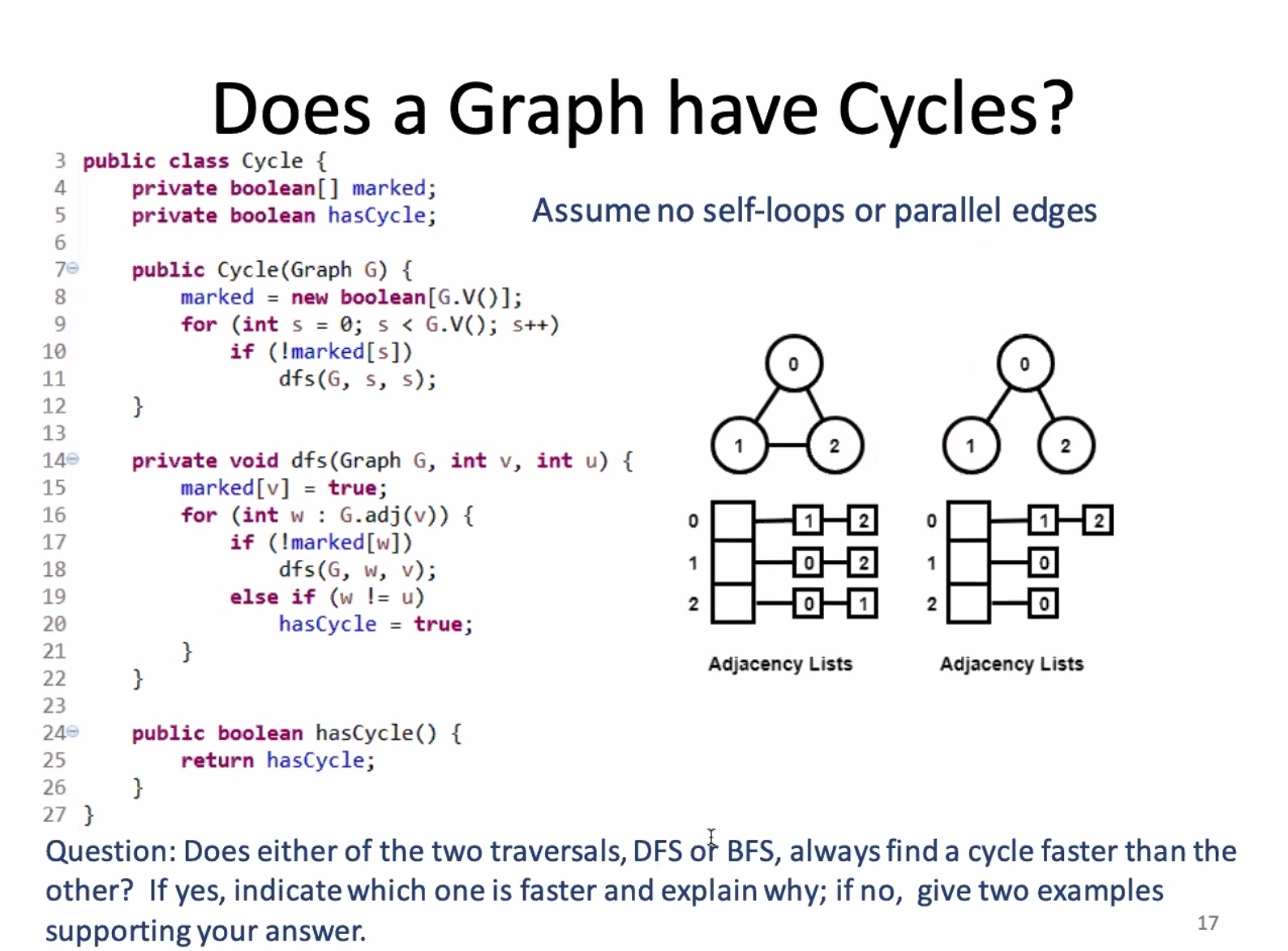
Performance:

• Worst case runtime is O(E) or O(V+E)
• Worst case space complexity O(V), when every vertice is added to the queue

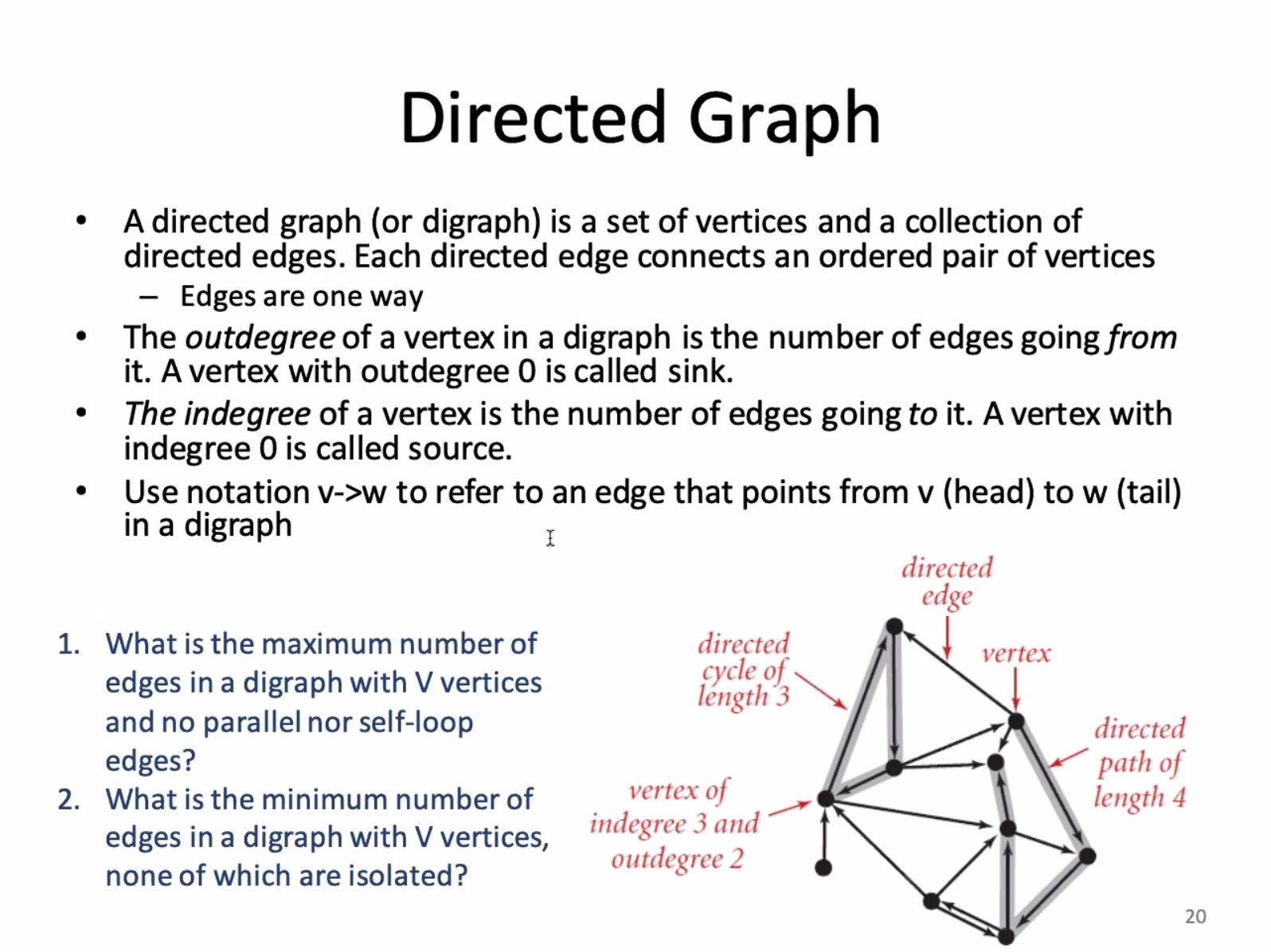
1. There is a maximum of (V(V-1)) vertices in a digraph with no parallel or self-loops. “Each edge can connect to every other edge.”
2. The minimum number of edges is (V-1).

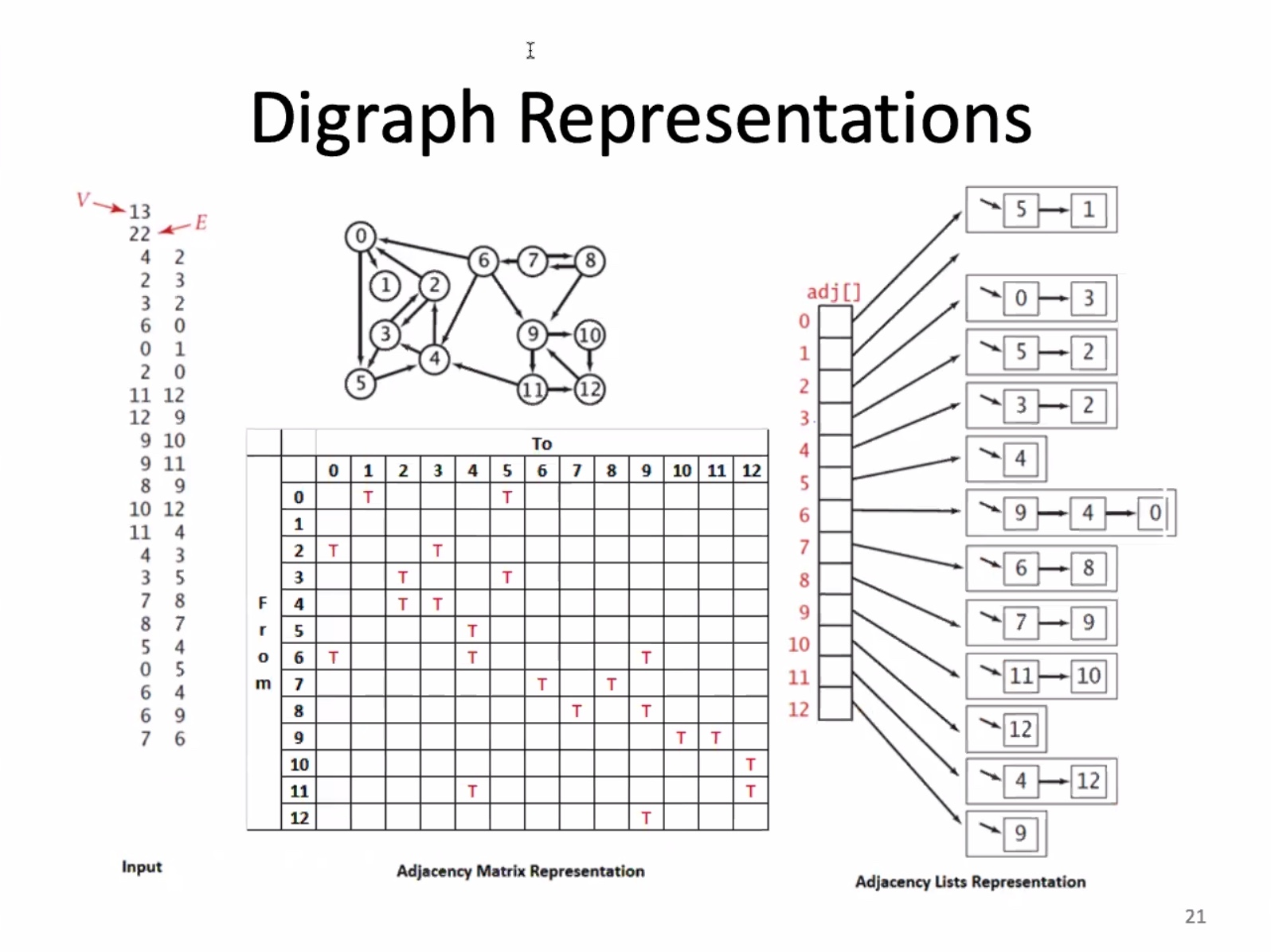
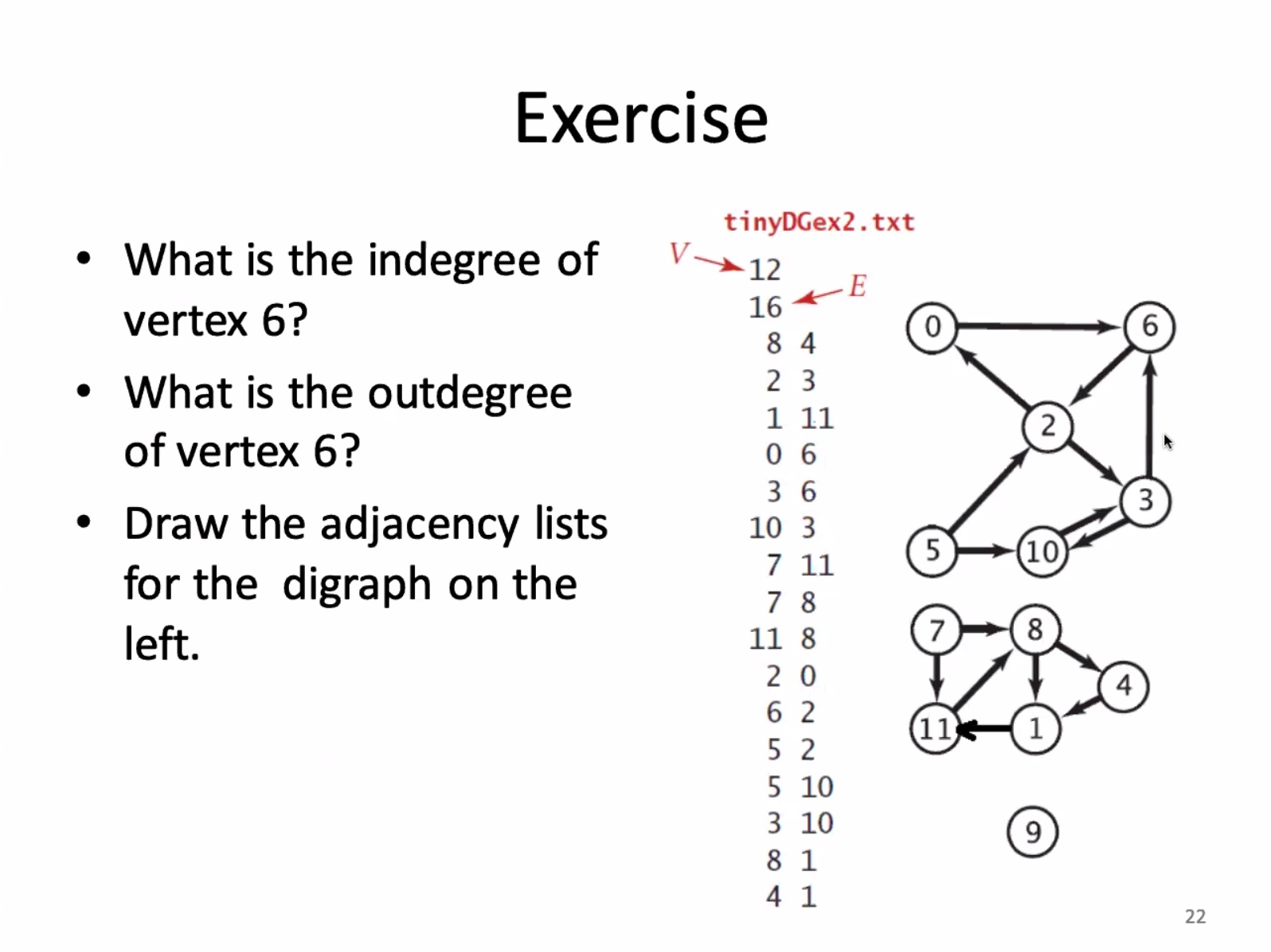
1. The indegree for 6 is 2
2. The outdegree for 6 is 1

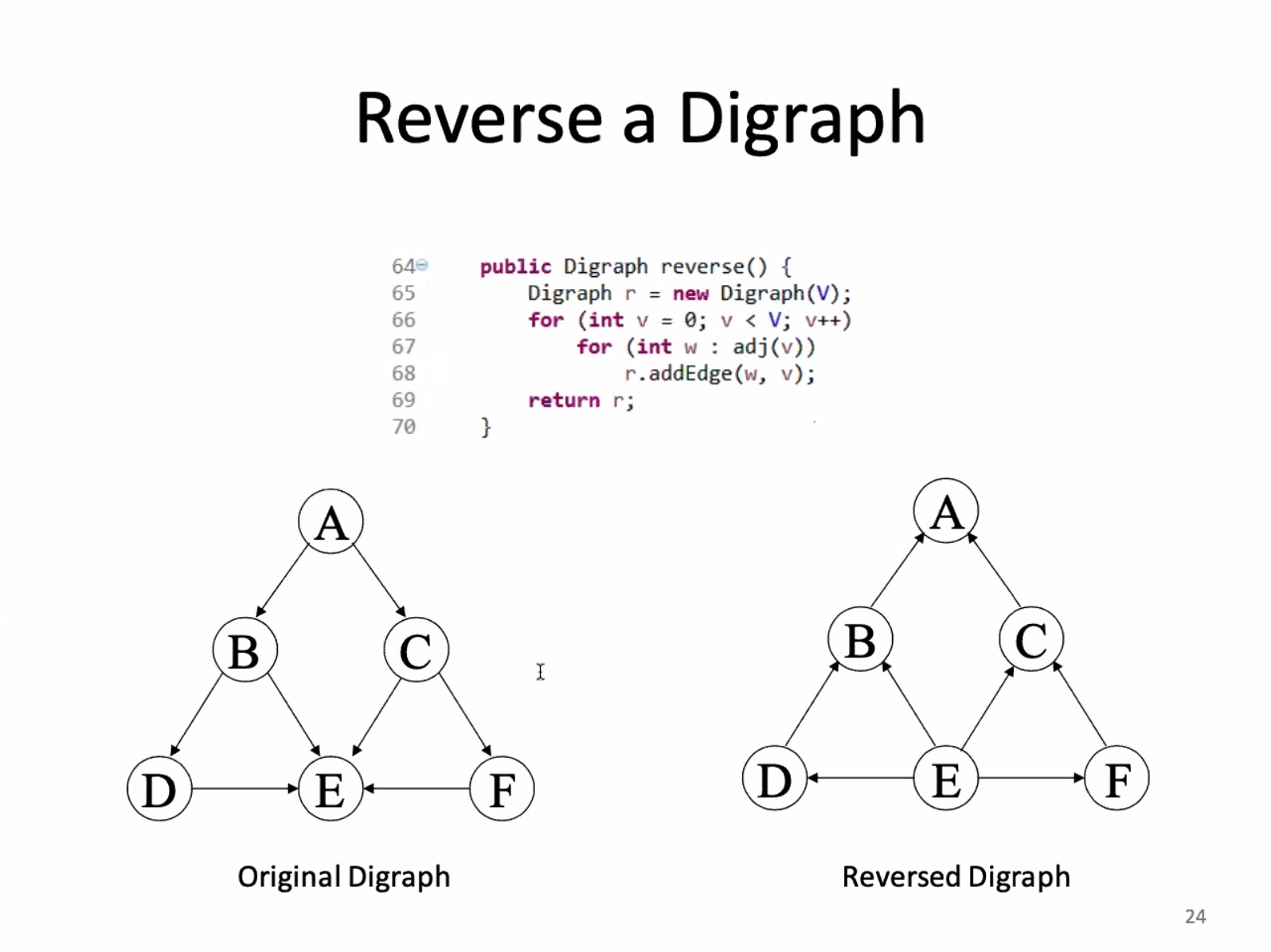
Space complexity of reverse is O(V+E). Runtime complexity is O(V+E).

What vertices are reachable from

• Source 1: 1
• Source 2: 0, 1, 2, 3, 4, 5
• Source 1,2,6: All except 7 and 8

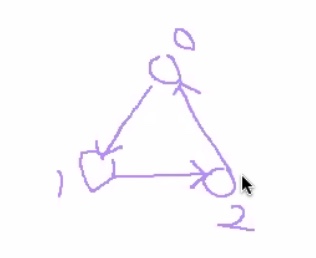
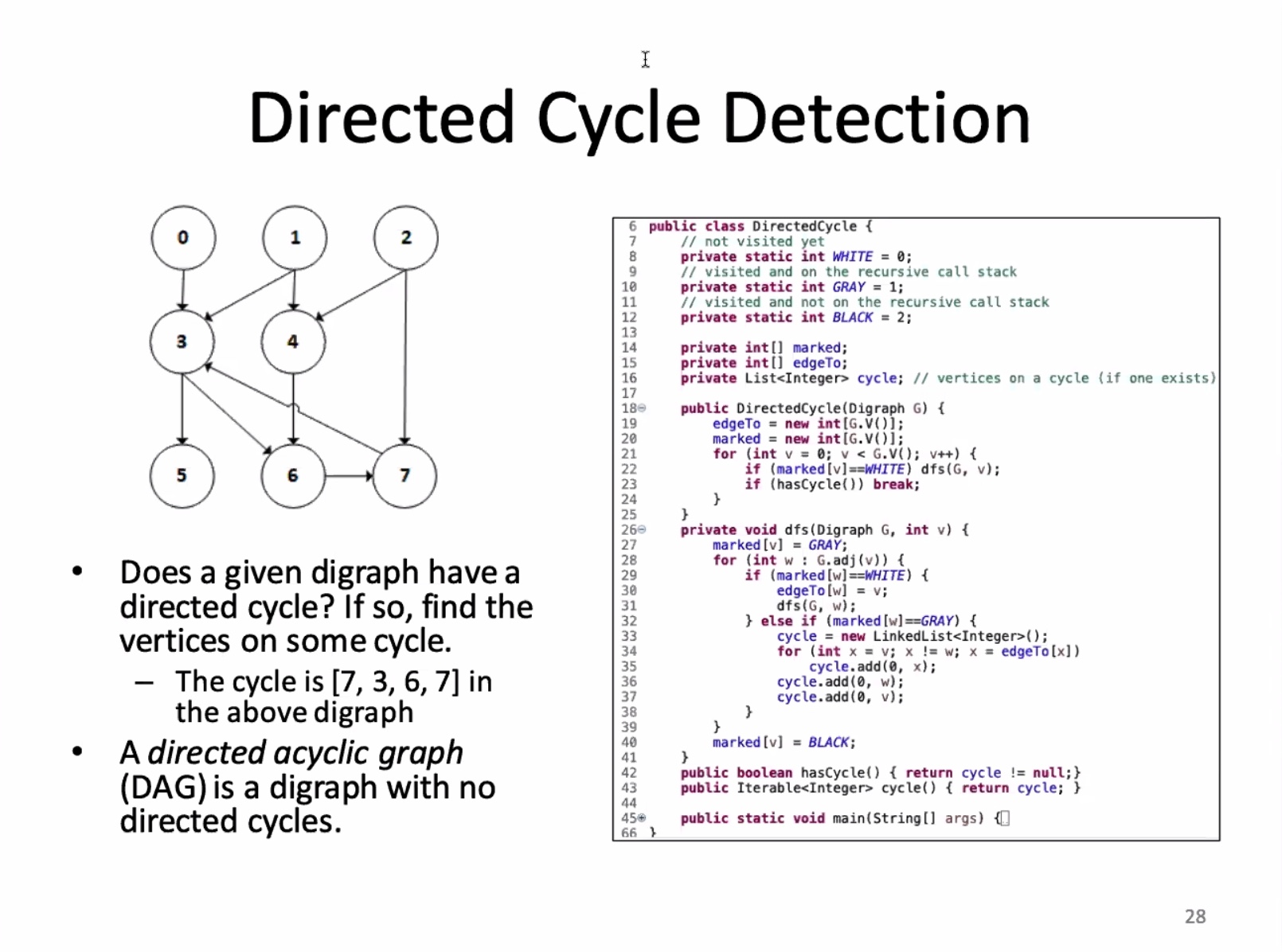
Directing cycle

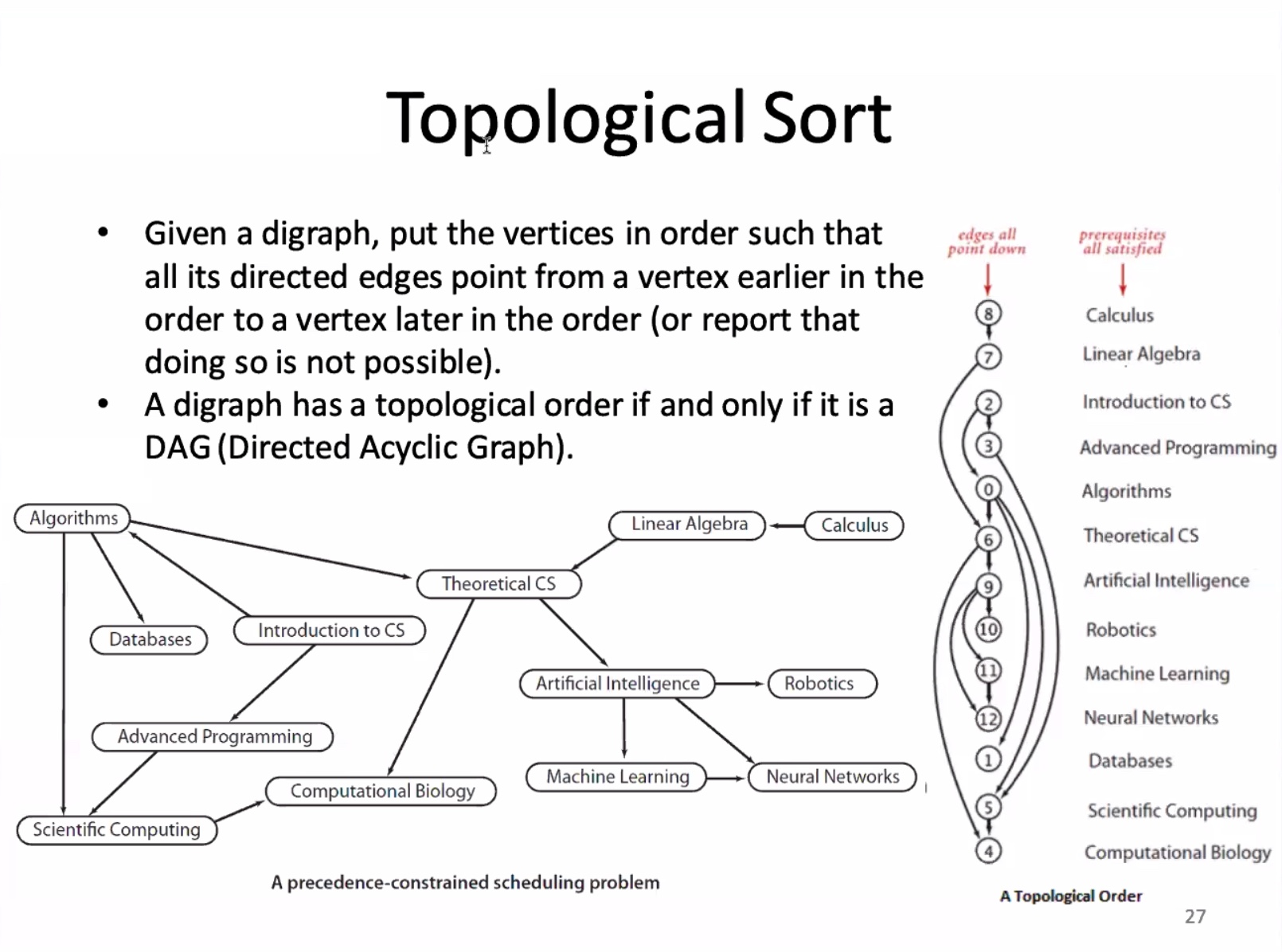
This would be impossible to take any courses. There cannot be any directed cycles in the digraph, it would be impossible to find the topological order. (This is a DAG).

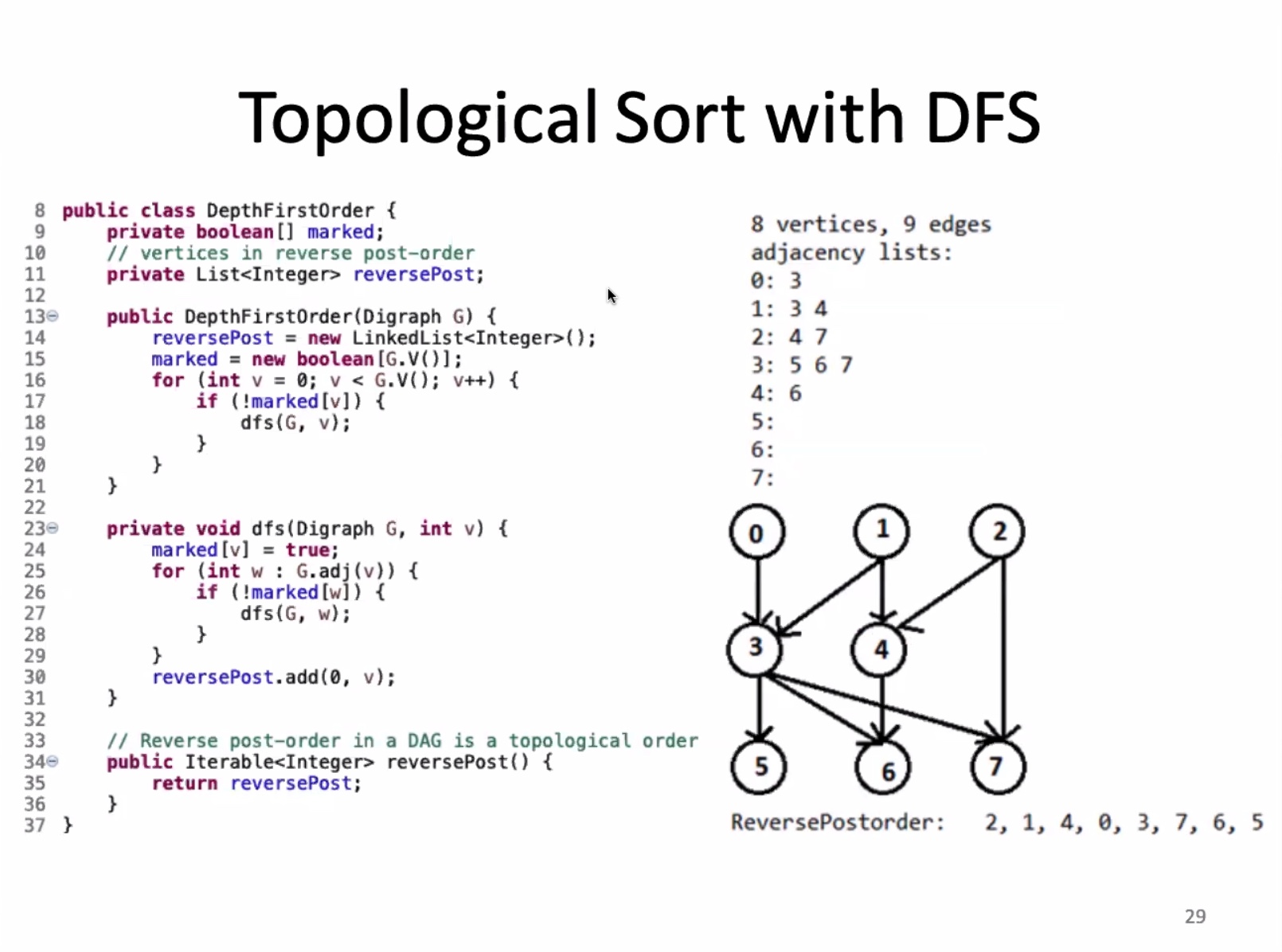
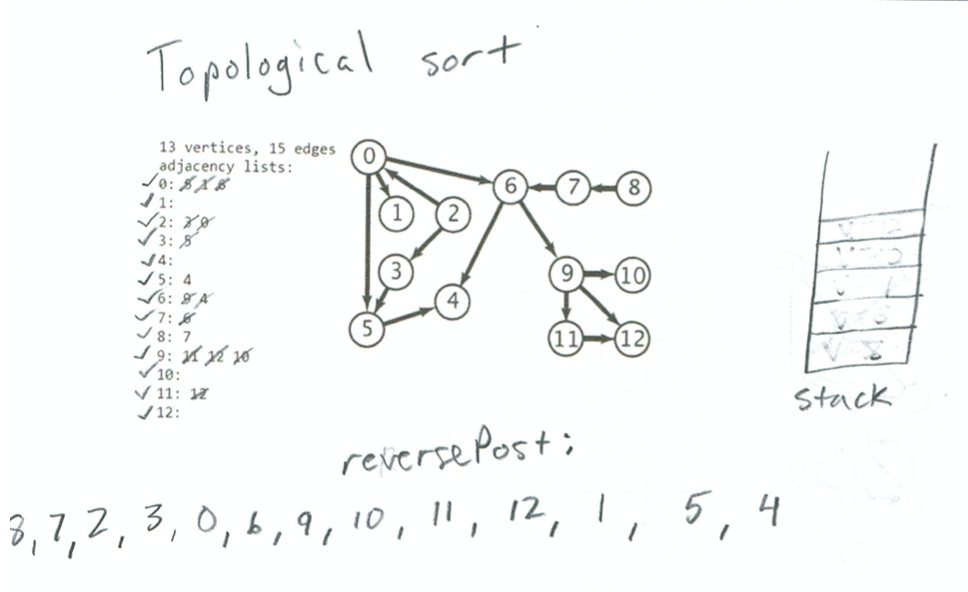
Topological sort with DFS trace

Vertexes in different color have been visited

0, 3, 7, 6, 5 are reachable from 0. Now go by vertex order and check 1

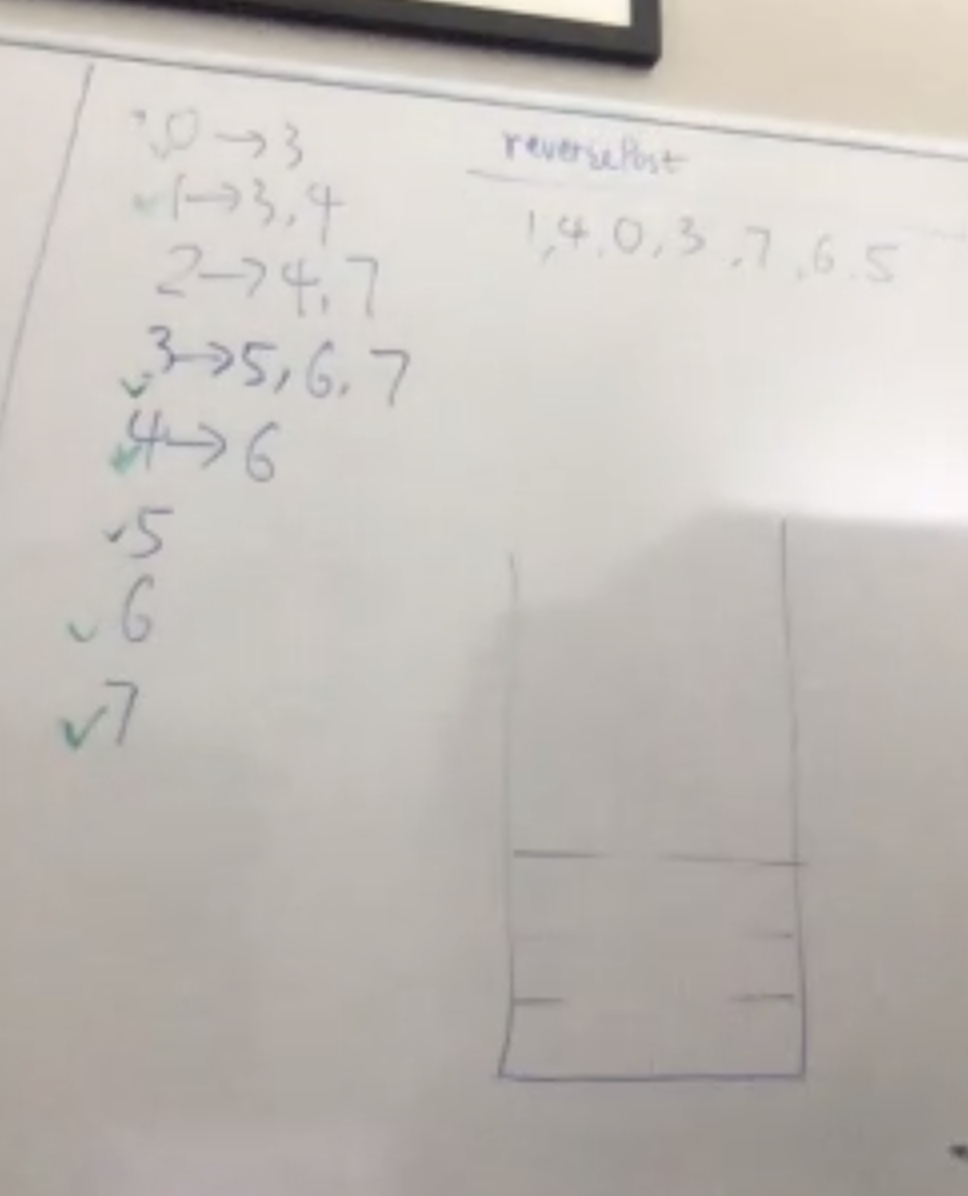
Now check 2

Everything has been visited now. Our reversePost is finished. All edges flow from left to right.

The runtime for the constructor is O(V+E). Space complexity for the constructor is O(V).

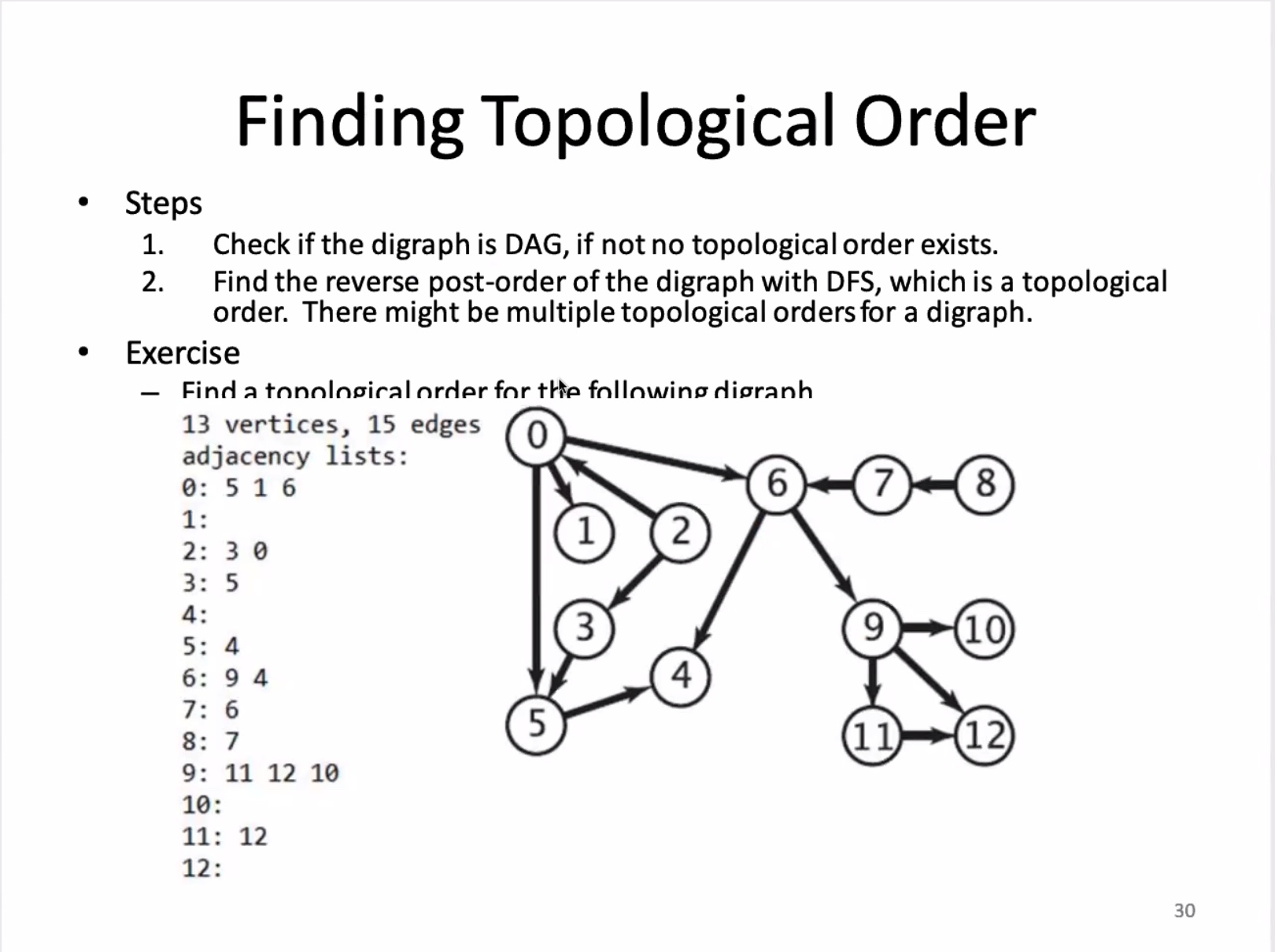
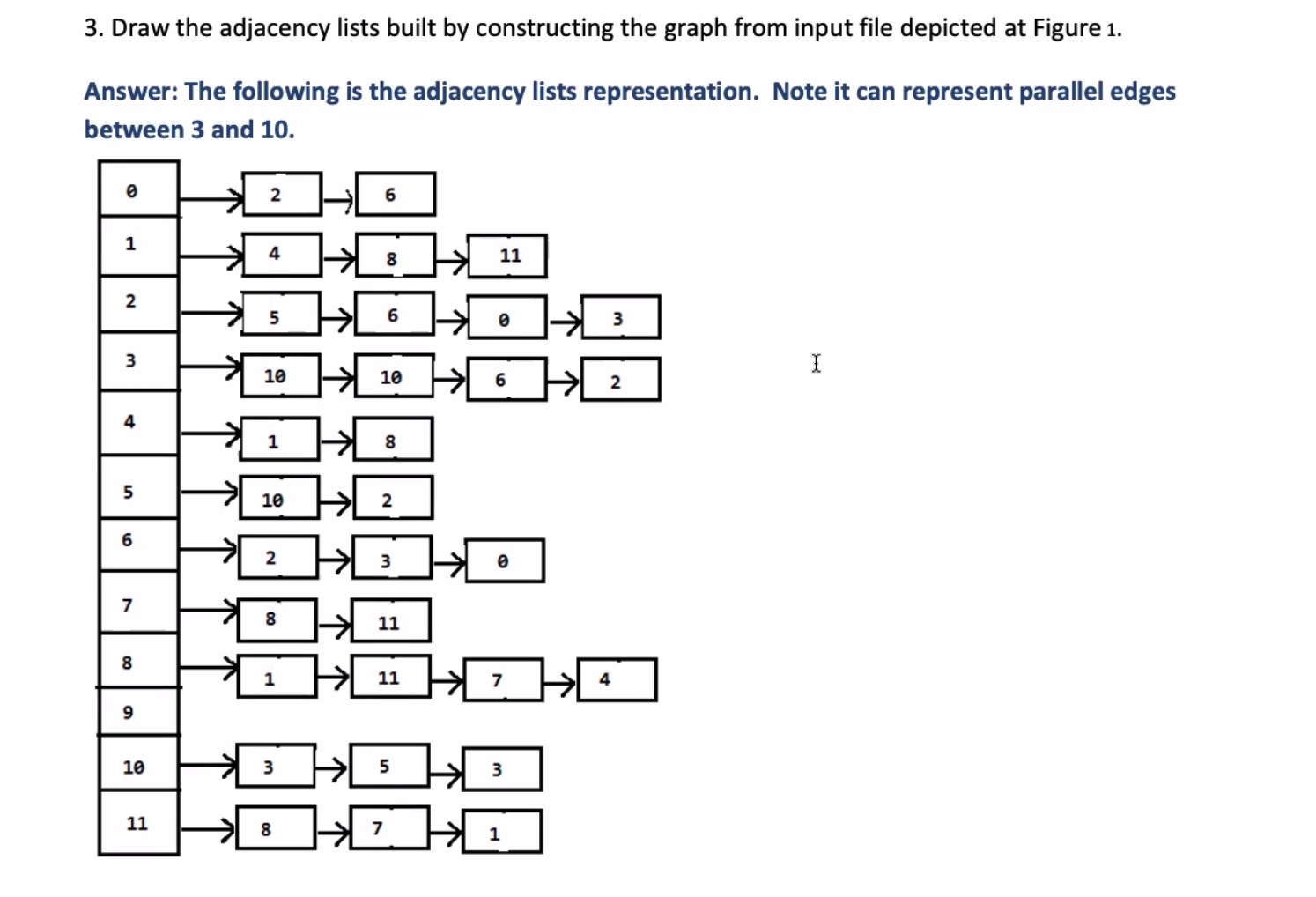
0: 6
1: 11
2: 0, 3
3: 6, 10
4: 1
5: 2, 10
6: 2
7: 8, 11
8: 1, 4
9:
10: 3
11: 8