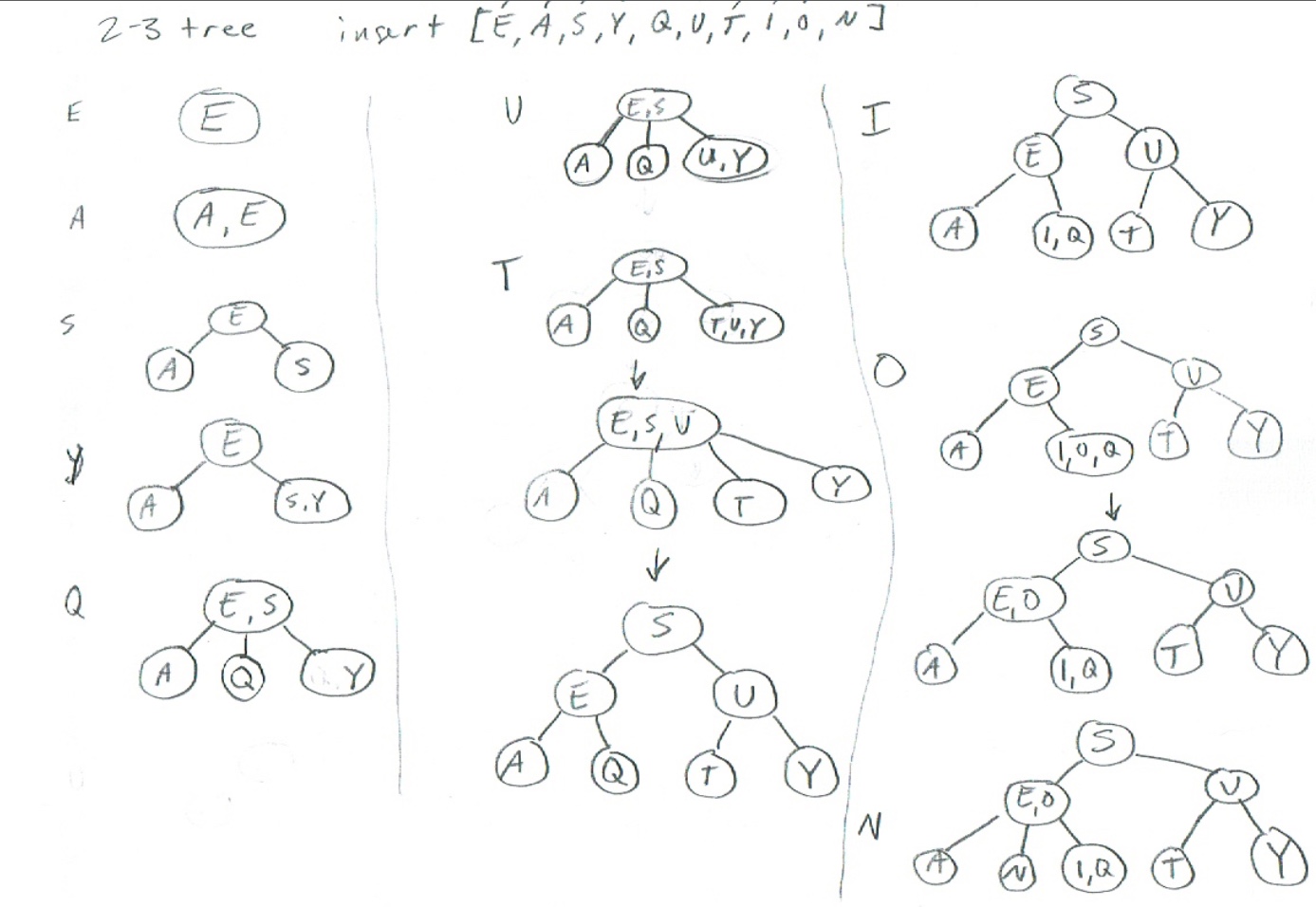
2-3 Tree #

1. An empty tree is a 2-3
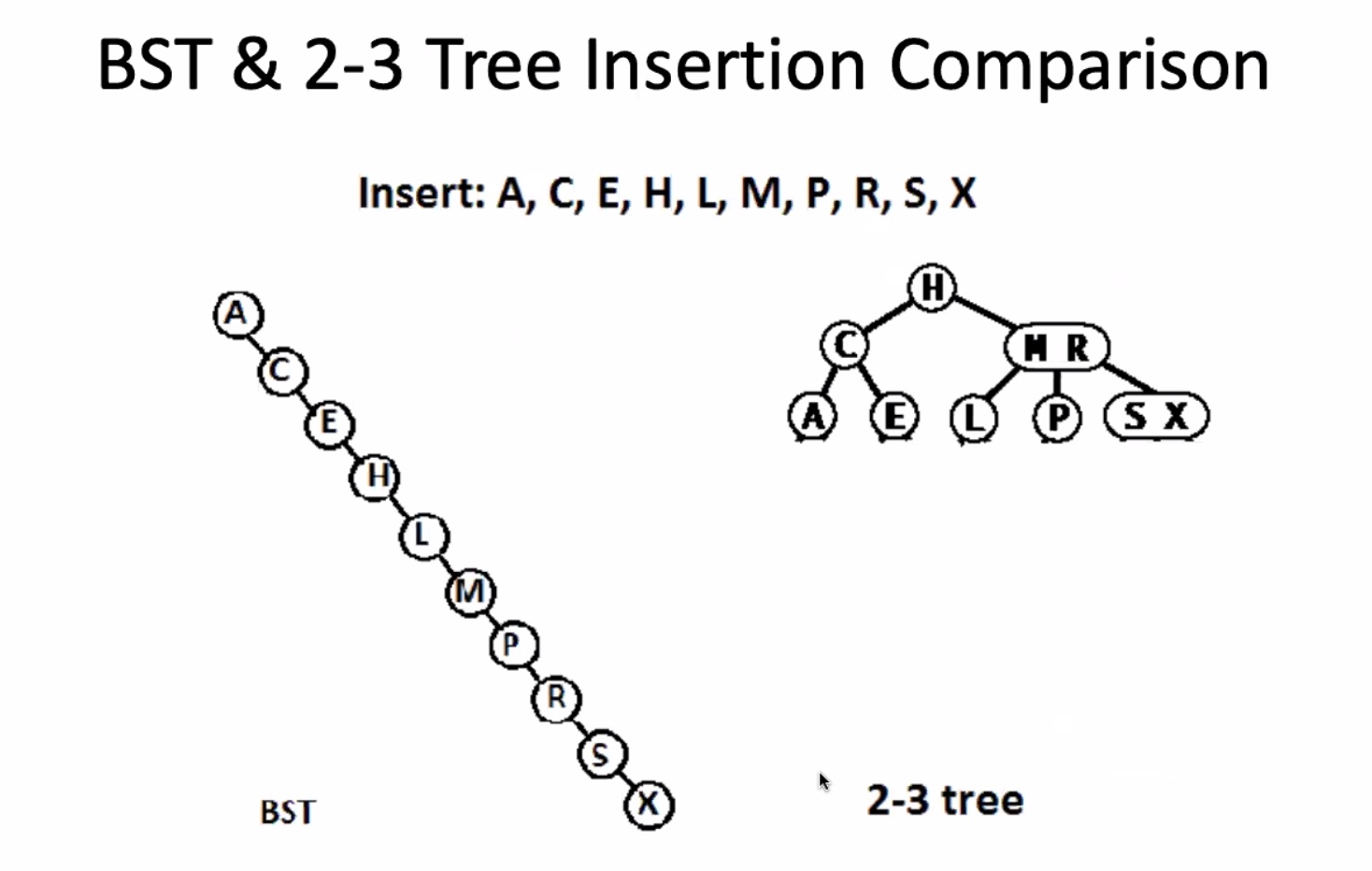
2. A BST is a 2-3 search tree
3. no
4. is yes

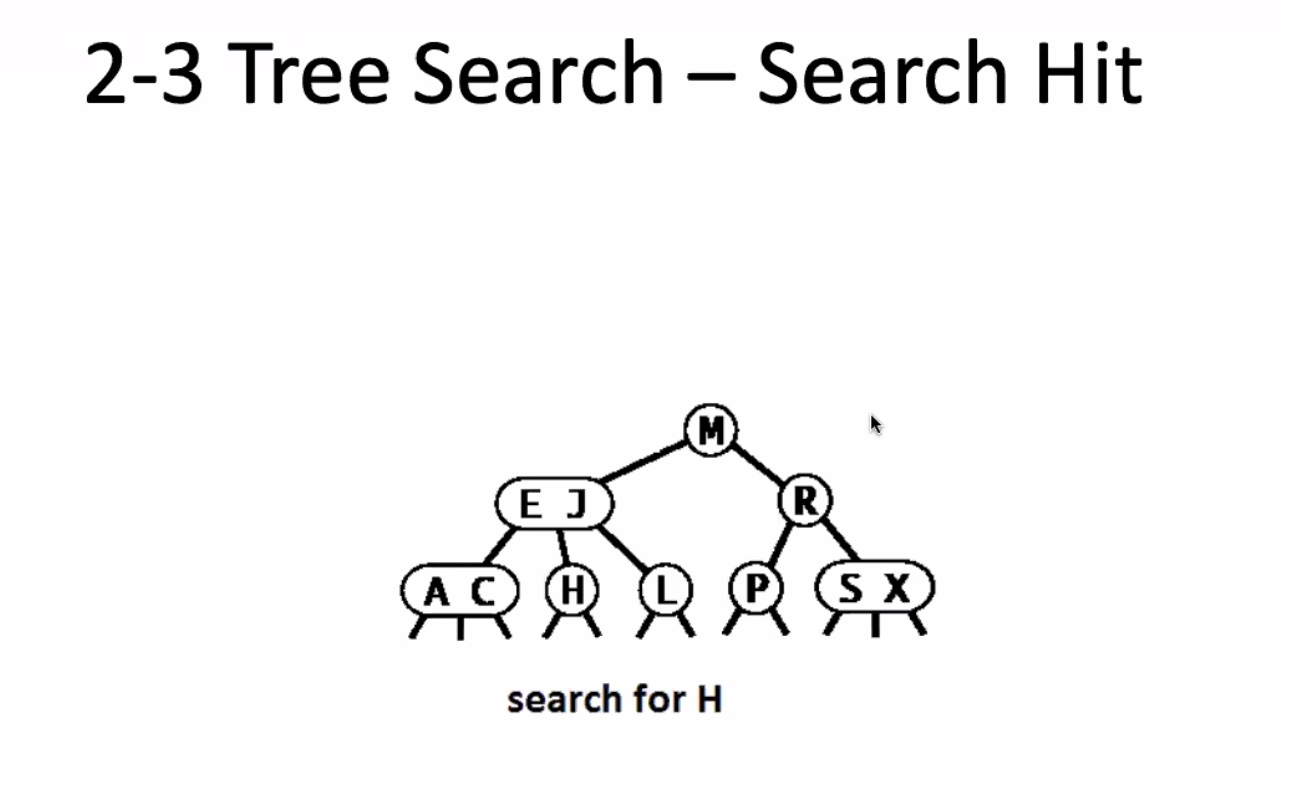
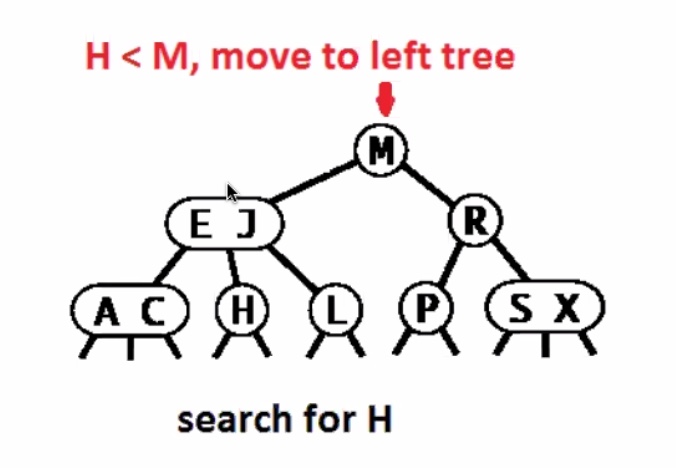
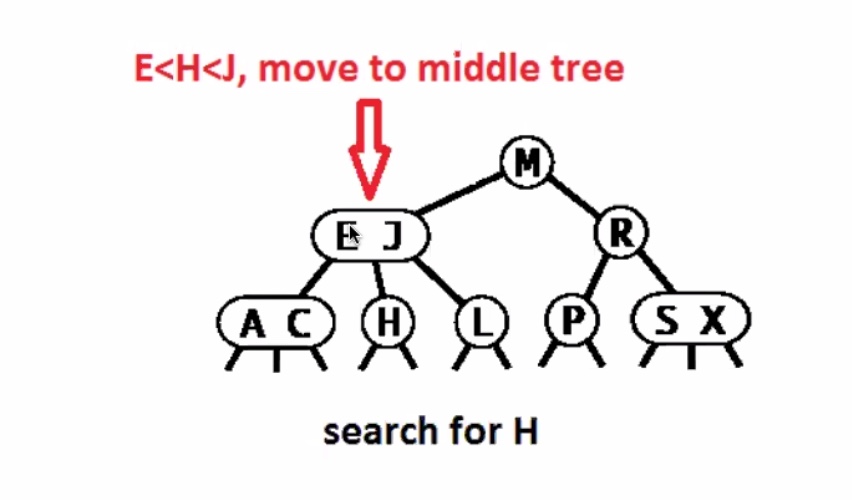
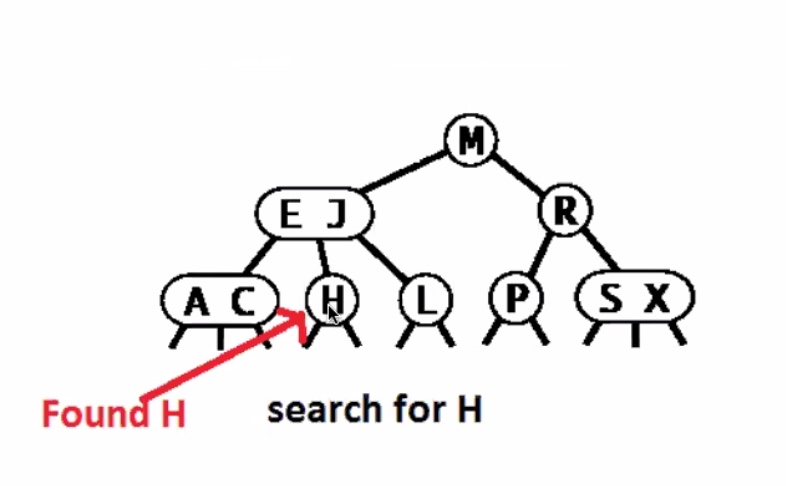
Search miss

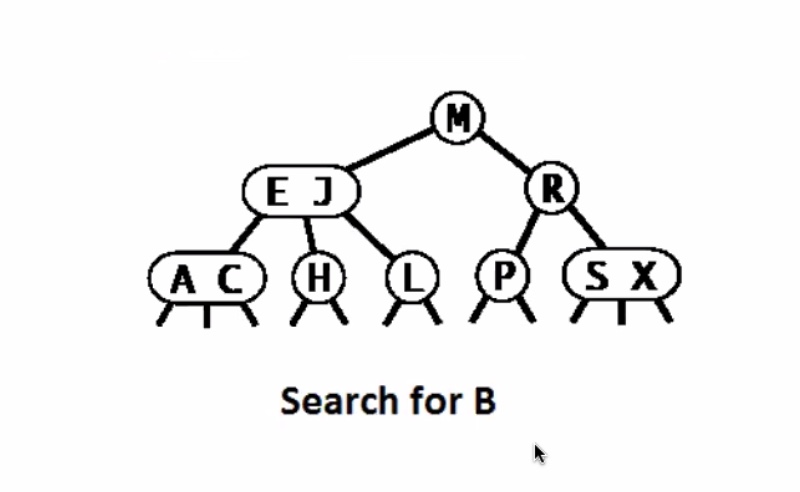
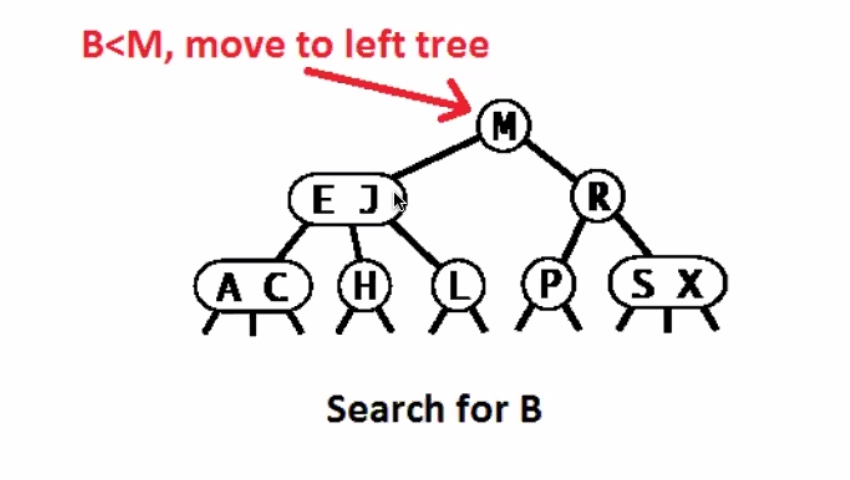
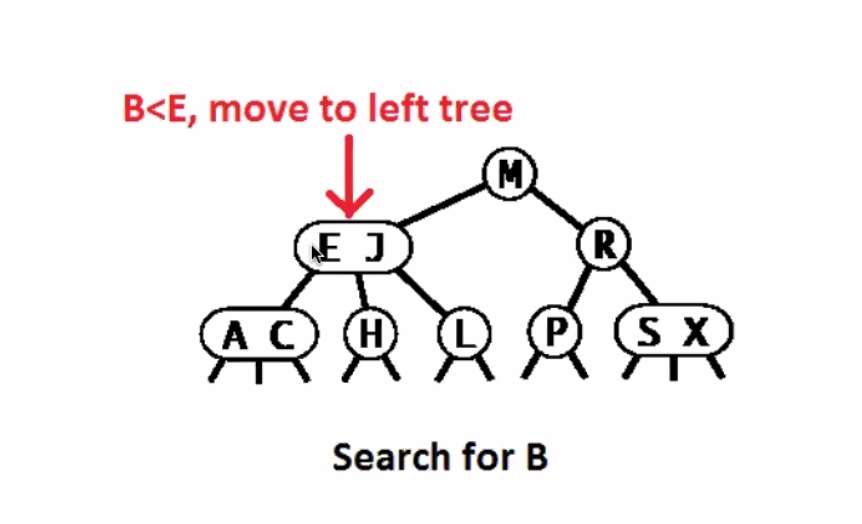
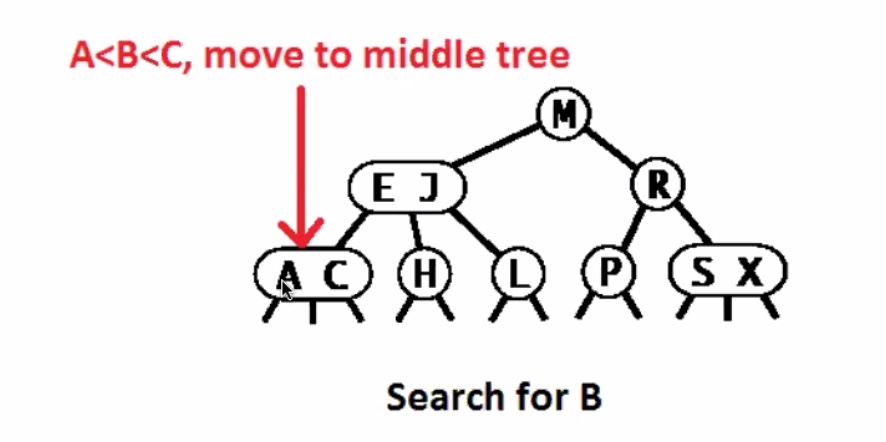
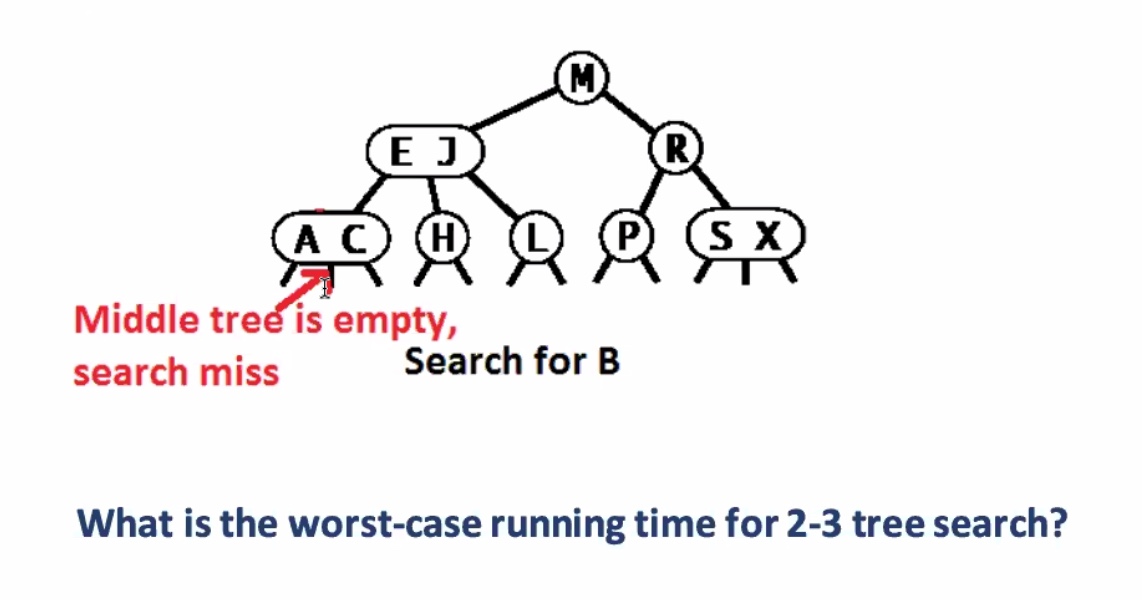
Worst case running time for 2-3 tree search is O(lgn). Remember the height of a 2-3 tree is between (floor(\log_3 N)) and (floor(log_2 N)). So in the worst case it searches the entire height of the tree + 1.

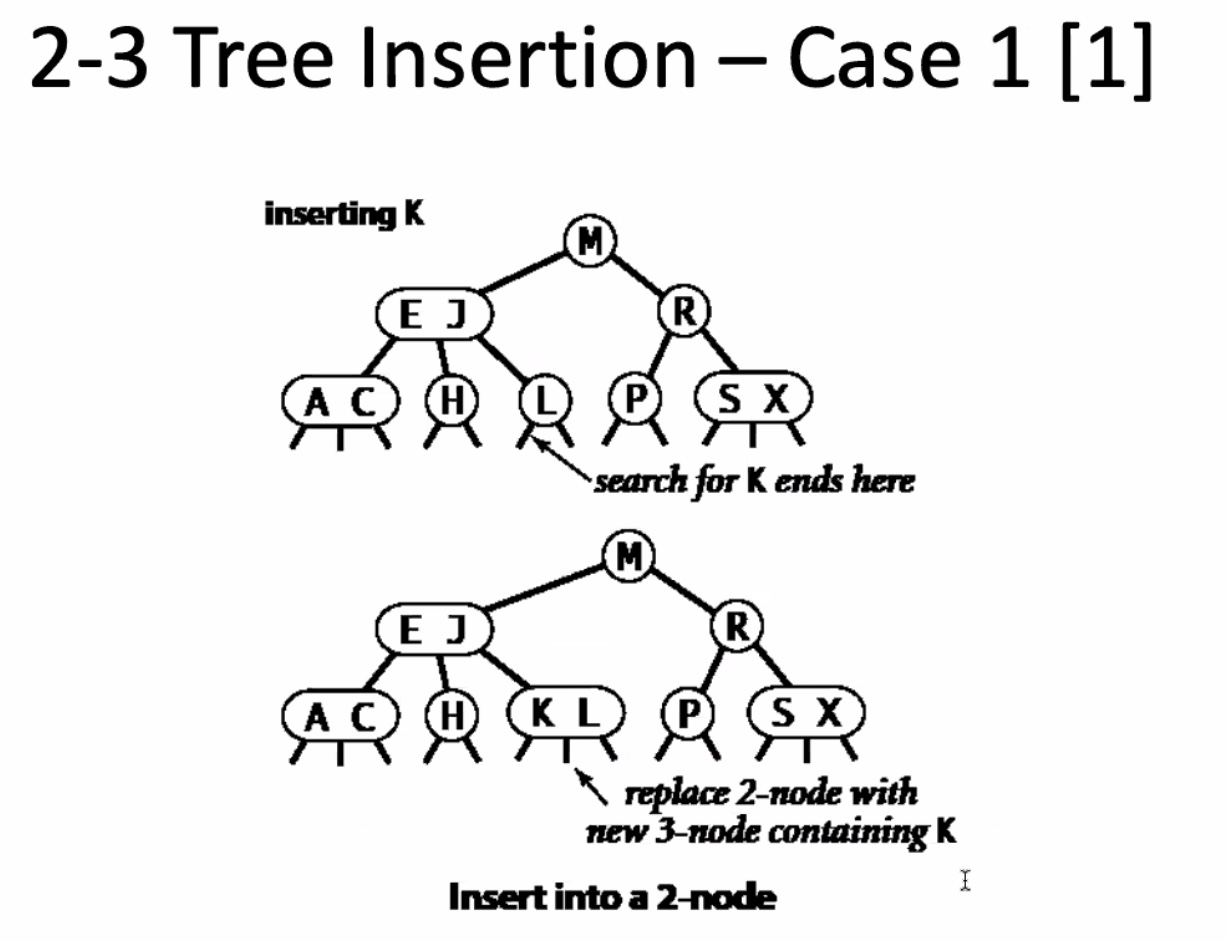
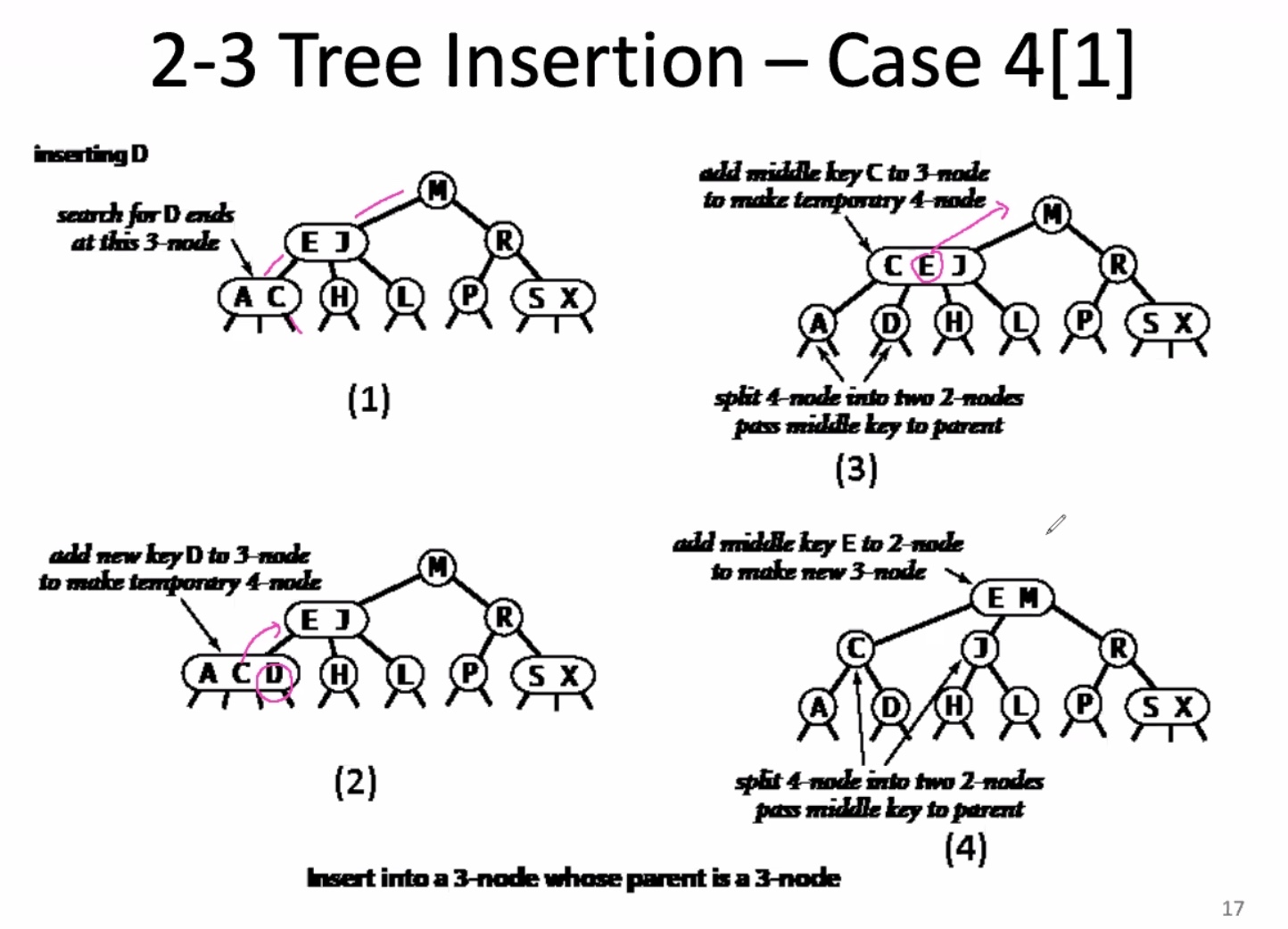
It inserts it into the 3 node to preserve the balance of the 2-3 tree.

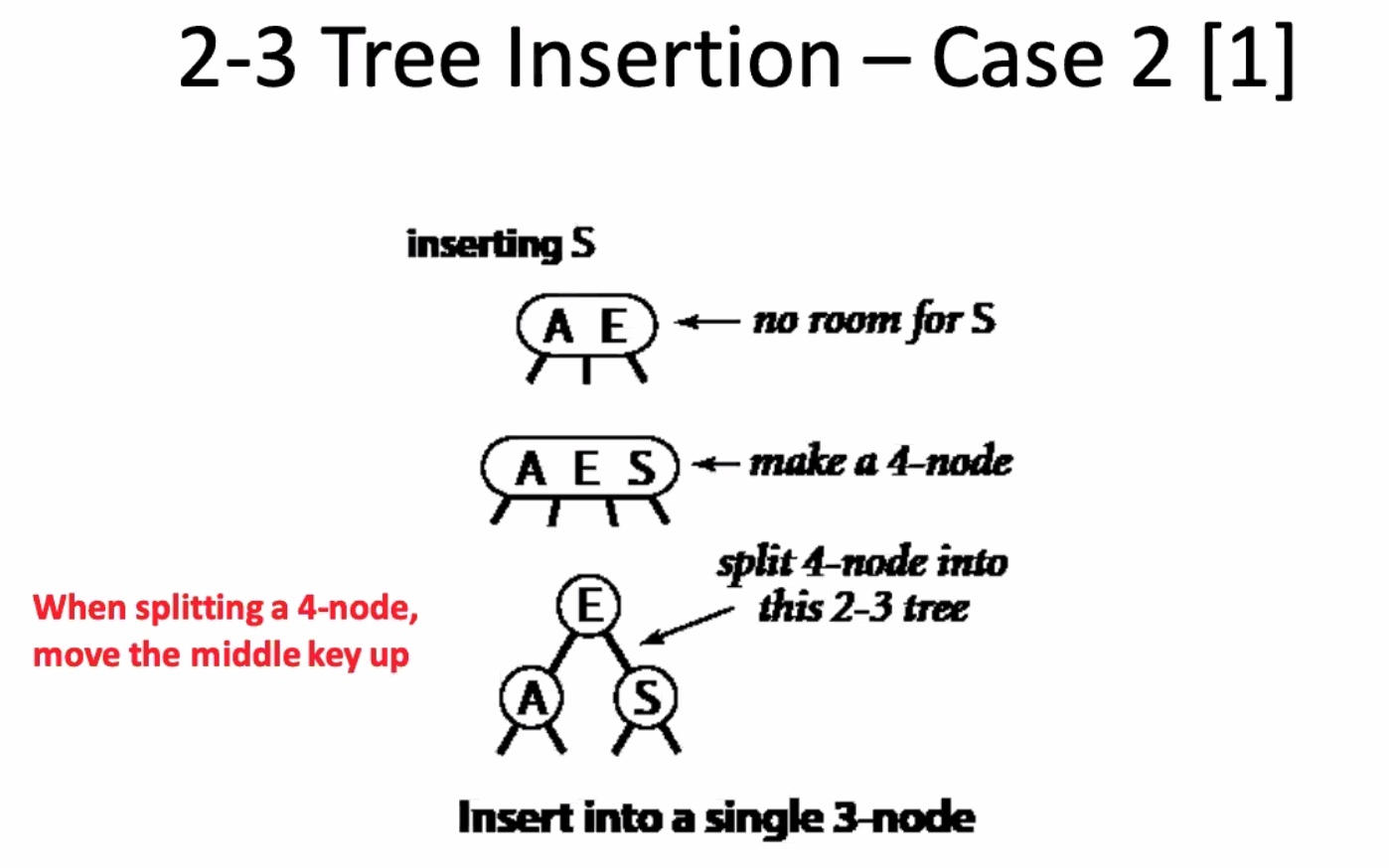
Creates a temporary 4 node, then it splits.

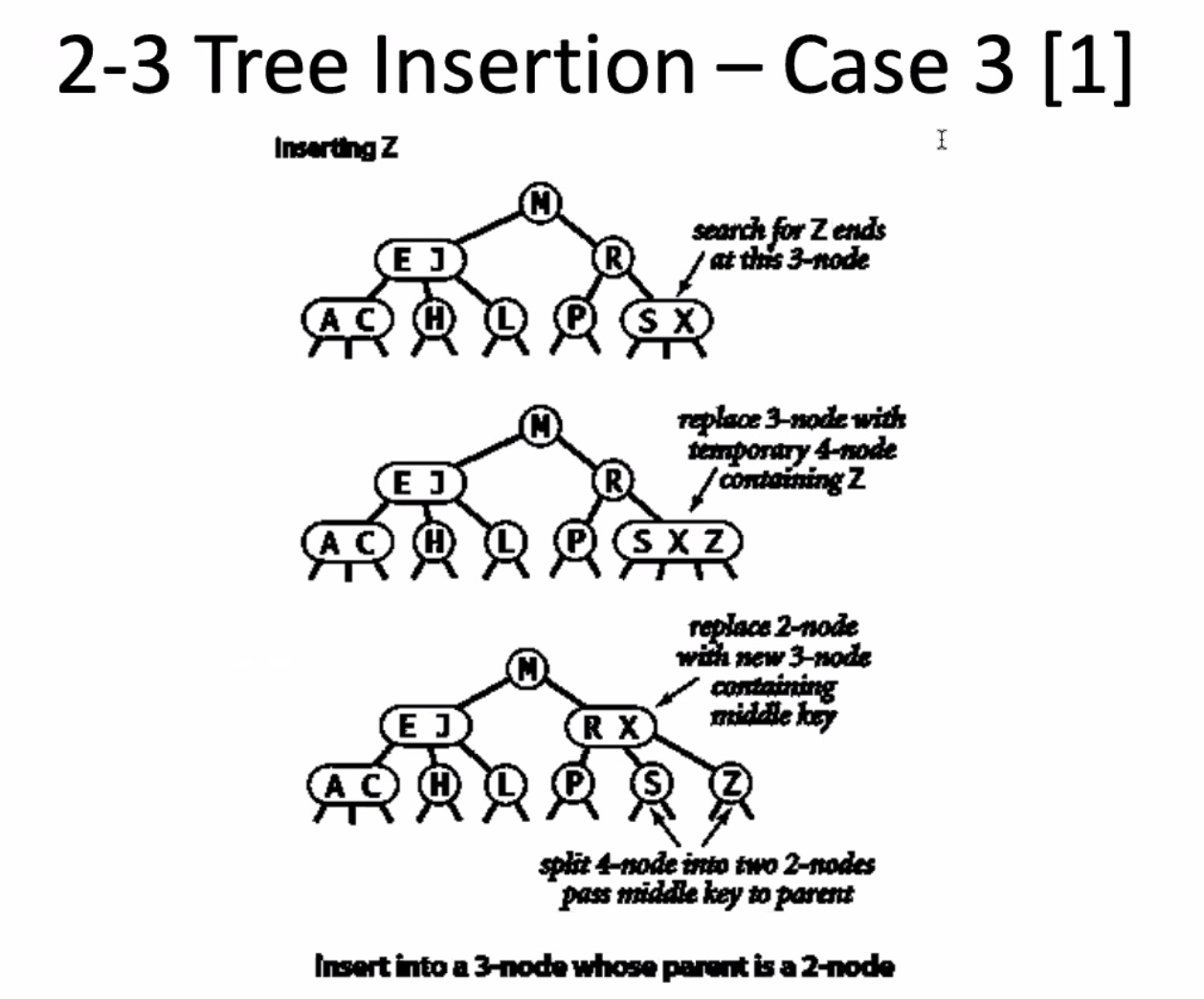
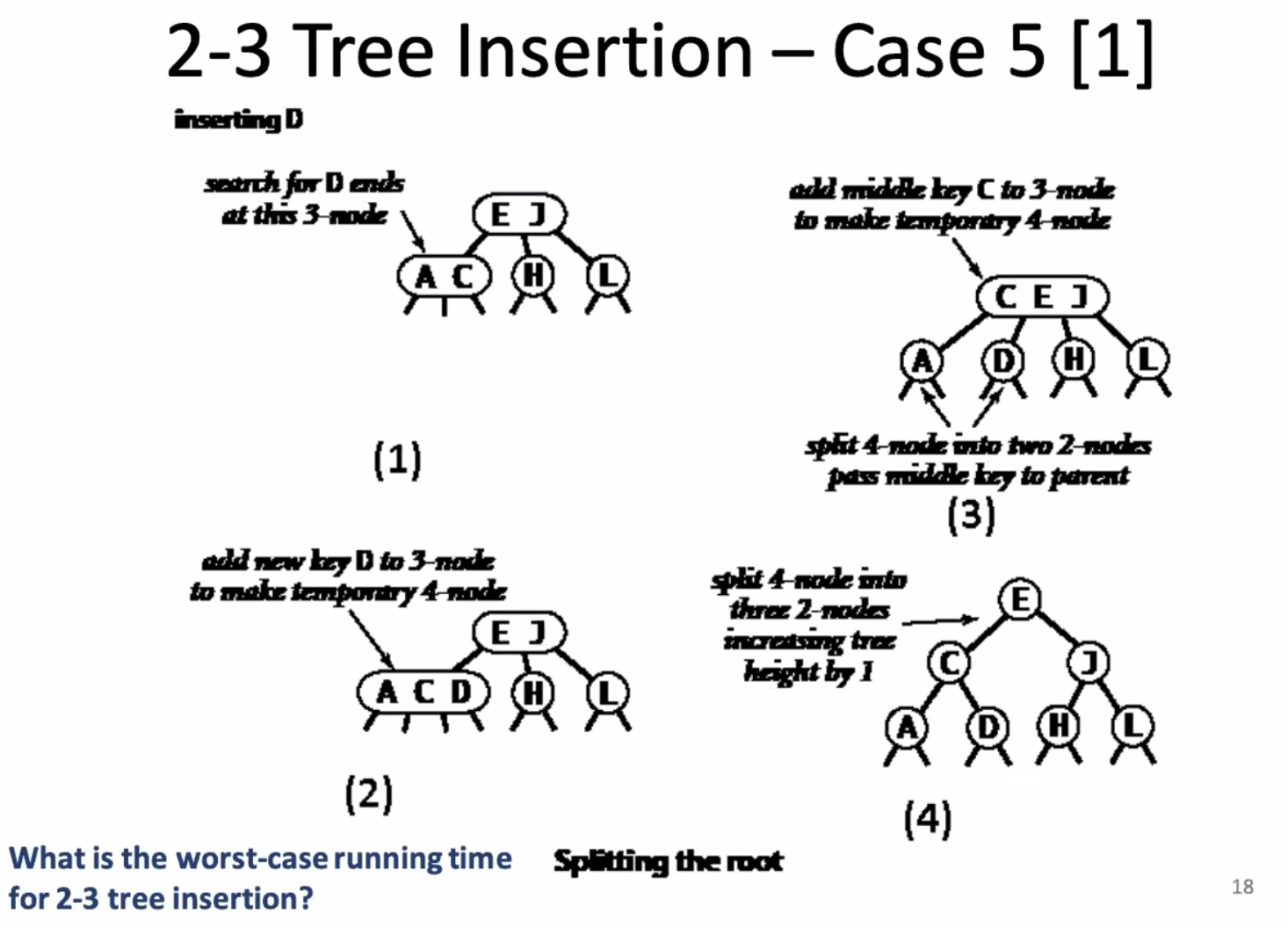
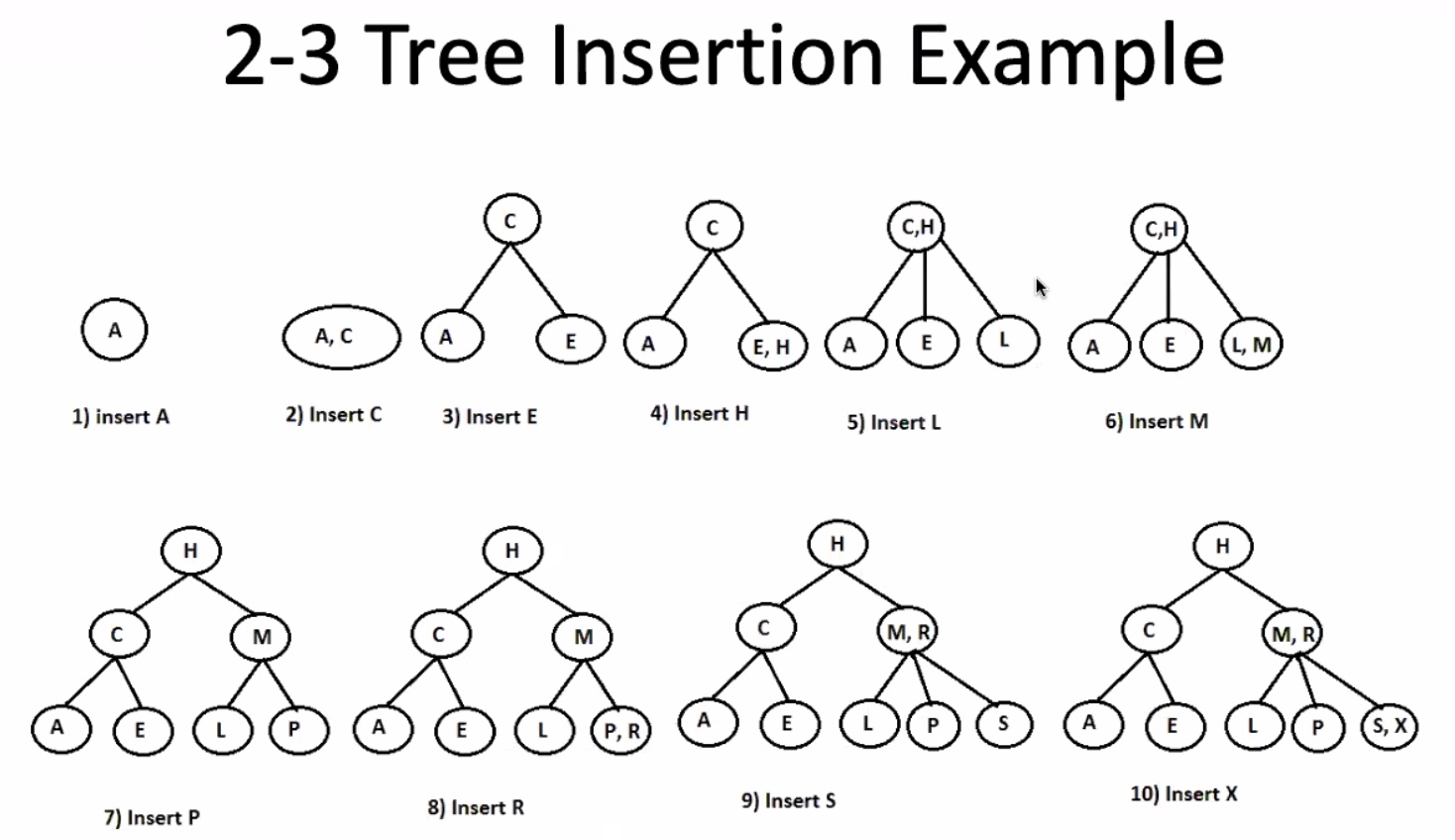
The worst-case running time for 2-3 tree insertion is O(lgn)

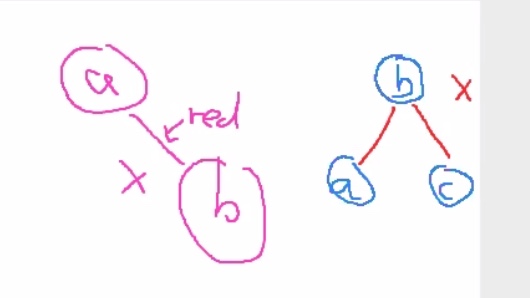
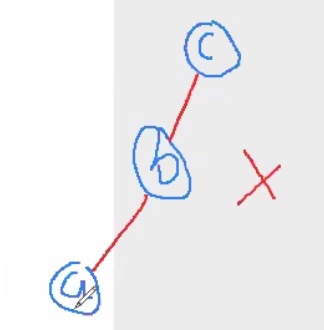
Invalid red-black BSTs

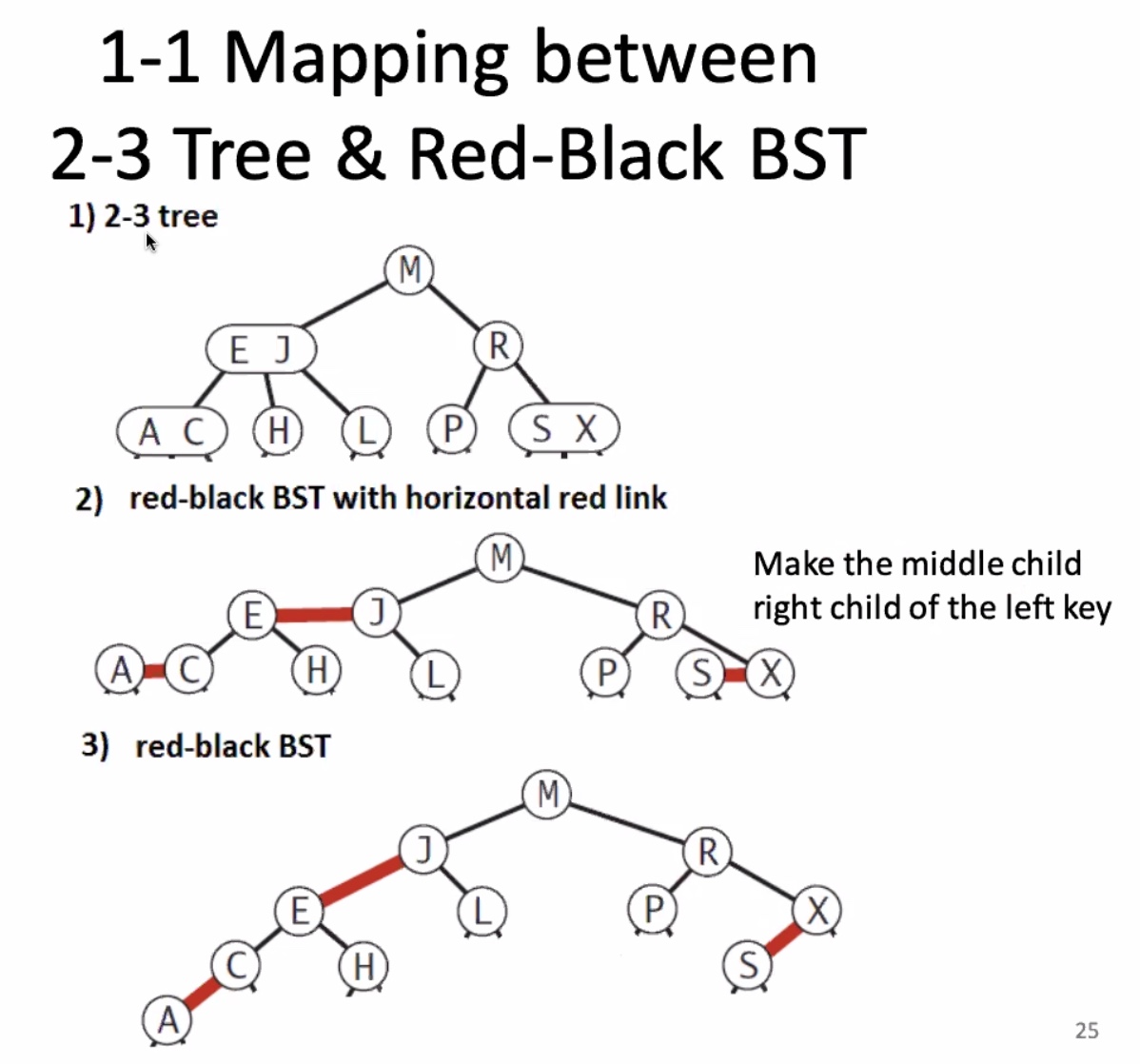
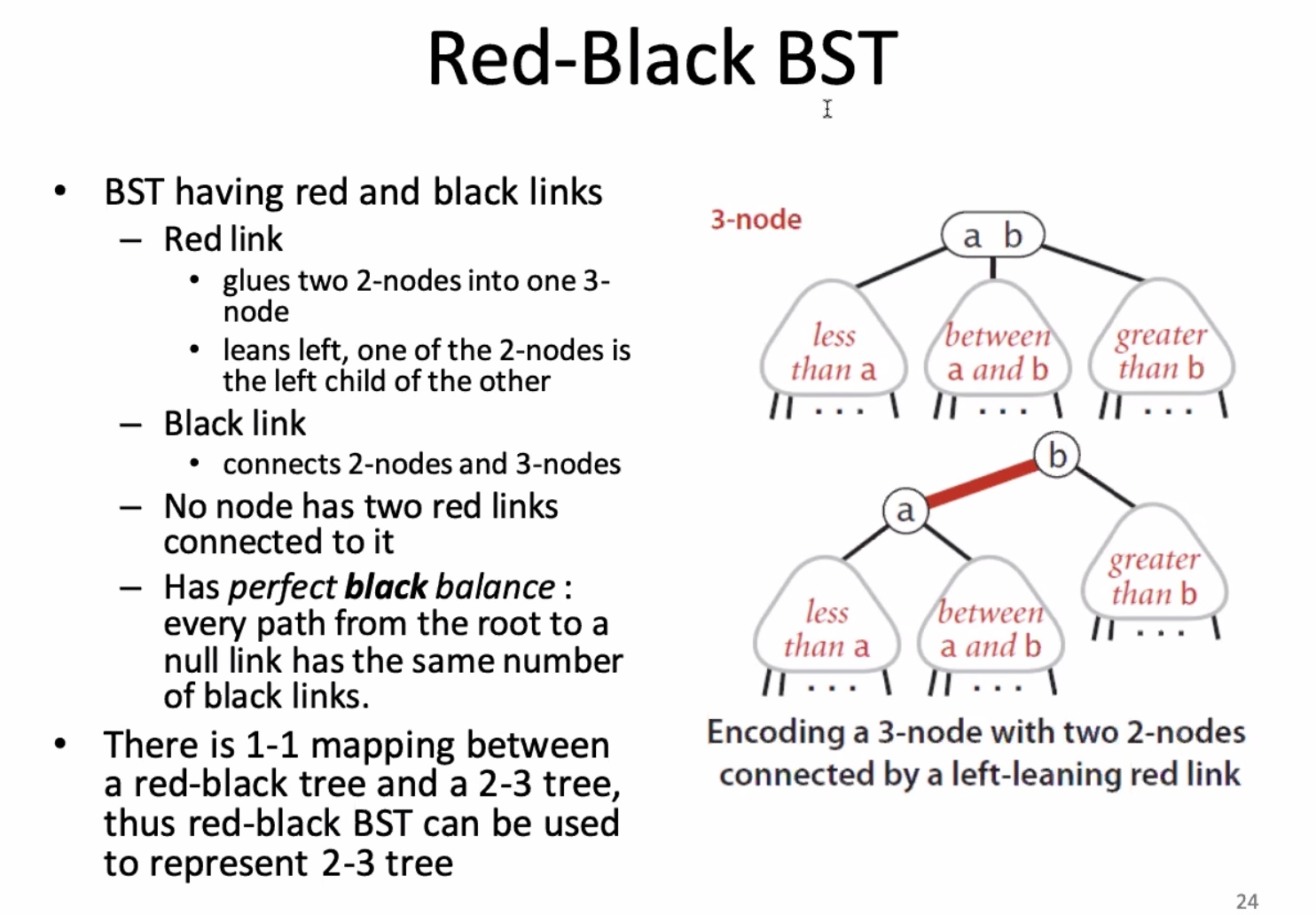
This is perfectly “black balanced” because each null leaf is 2 black links to the root. The height is 4 because you consider both black and red links.

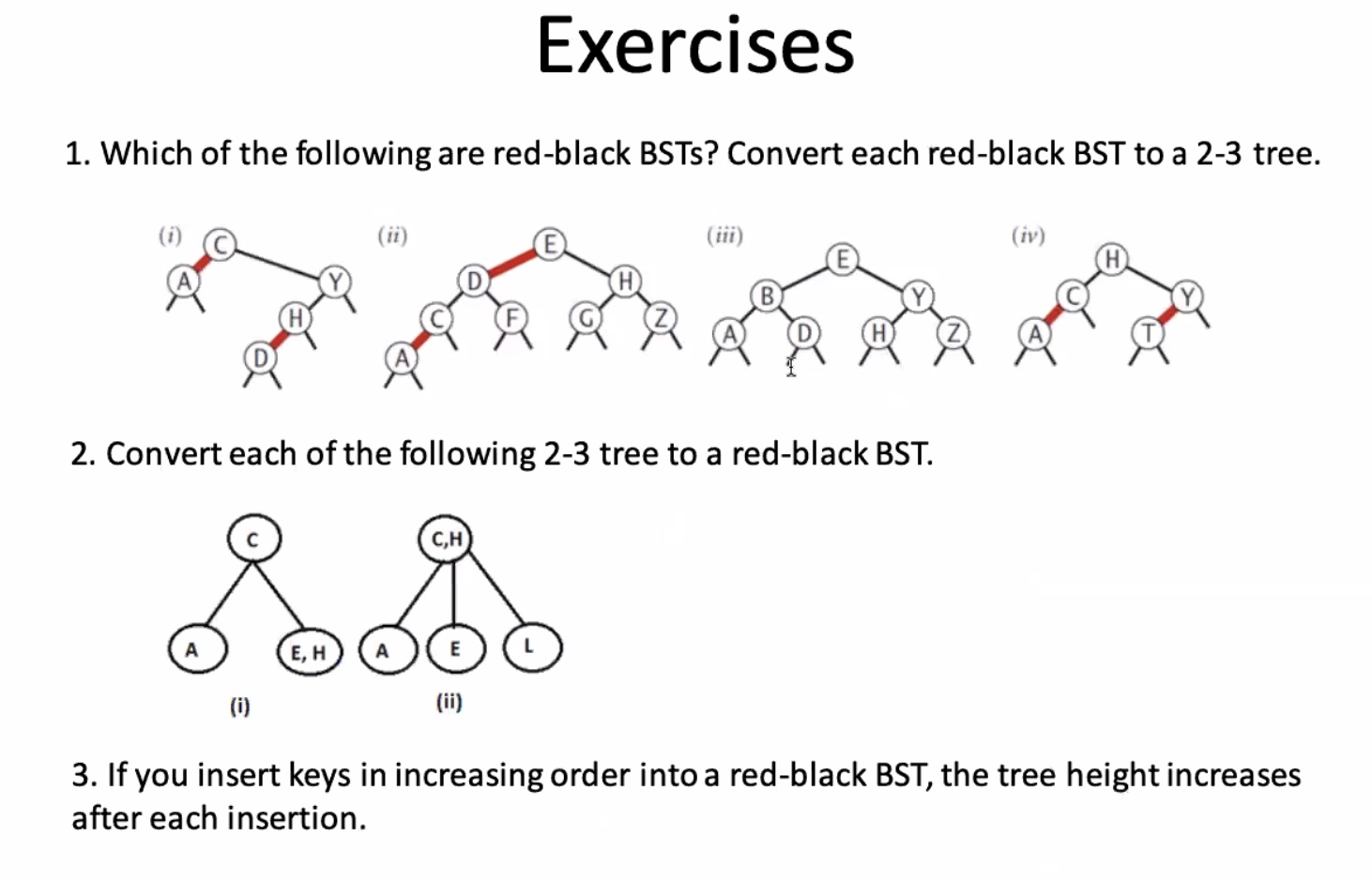
1. (i) is not black balanced, so not red-black BST (ii) is not black balanced, also key order is wrong, so not red-black BST (iii) is black balanced, special case where there is no red links (but they’re not required), so yes it is a red-black BST (iv) is black balanced, and red links are valid, key order is good, so red-black BST