Exercise solutions #
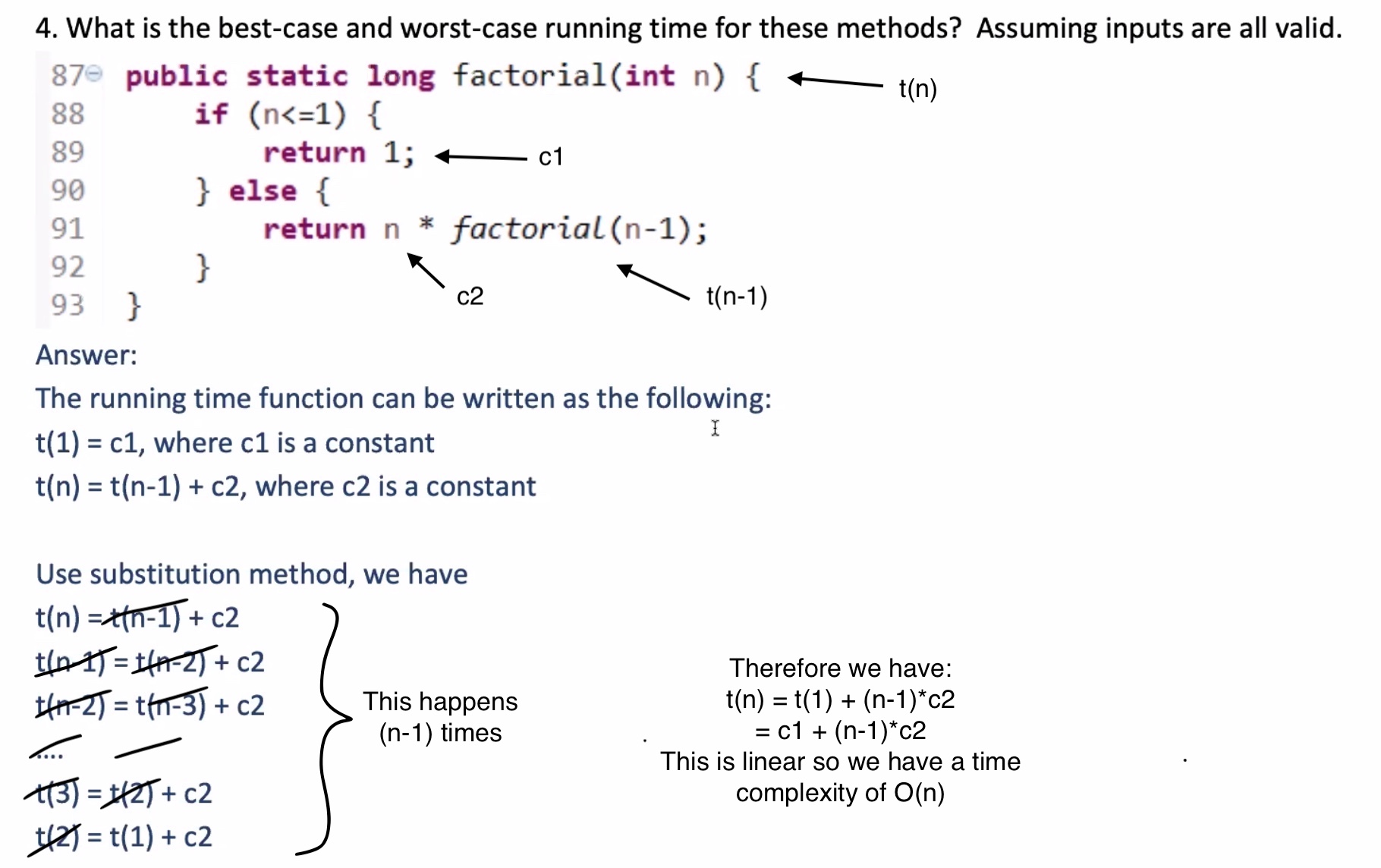

For example if \( n = 6 \) :
\[\begin{aligned} t(n) &= t(n) \cdot t(n-1) \cdot t(n-2) \cdot t(n-3) \cdot t(n-4) \cdot t(n-5) \\ &= \underbrace{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}_{\text{this happens} \,n\, \text{times}} \end{aligned}\]So we have a time complexity of \( O(n) \)



Space complexity cont. #

Time complexity of this is \( O(n) \) . Space complexity is \( O(1) \) .
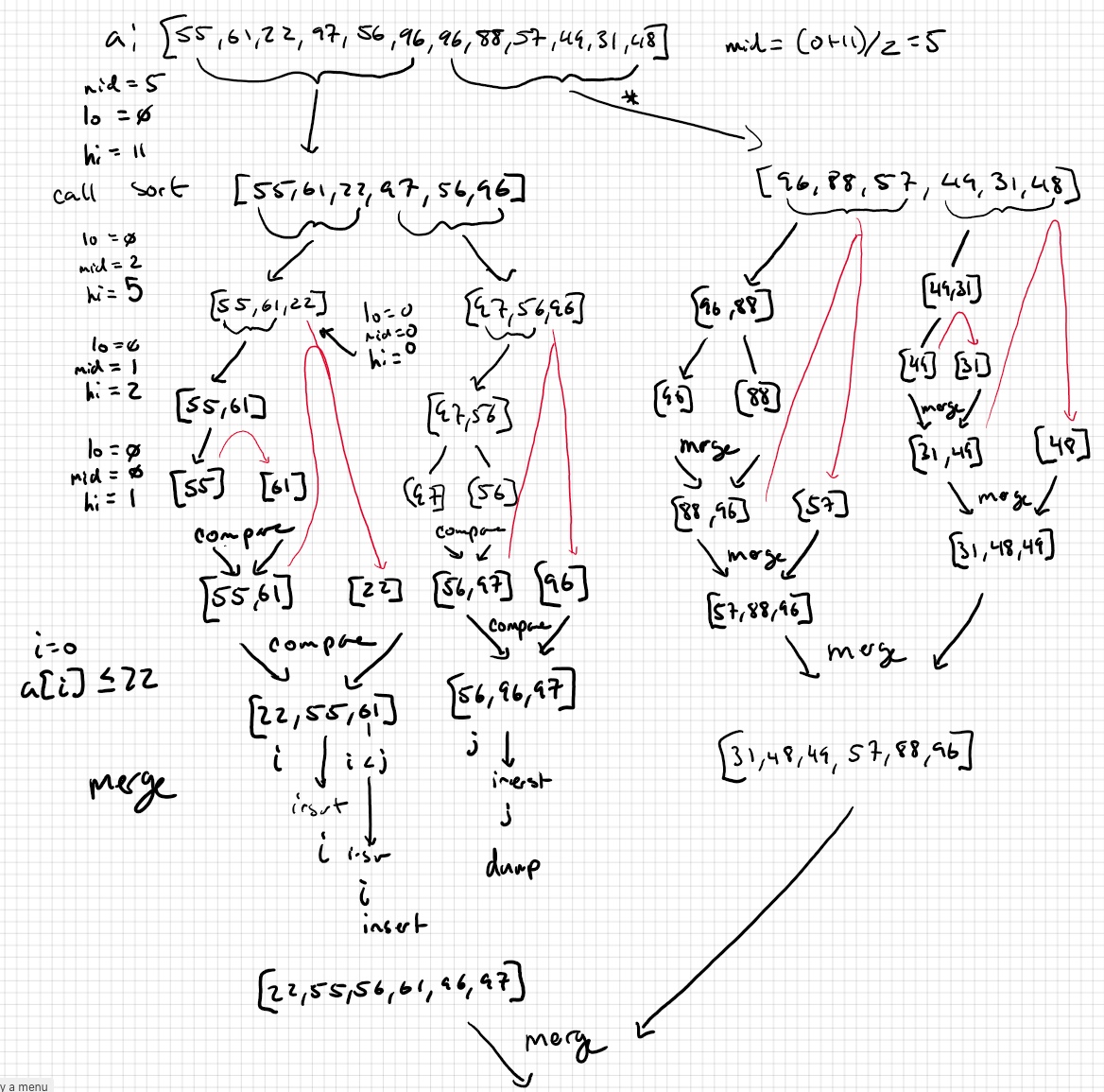
Sorting #


Requires 2 smaller arrays already sorted.

Compares the two elements under the cursors, sorted into a new array in non-decreasing order. Copy the smallest one to the destinatino array, and move the cursor forward on respective array.


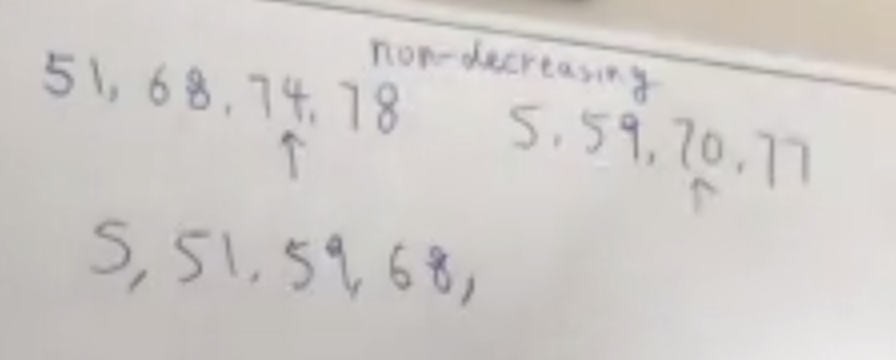



When one cursor goes past the end of an array you just copy the other cursor over.
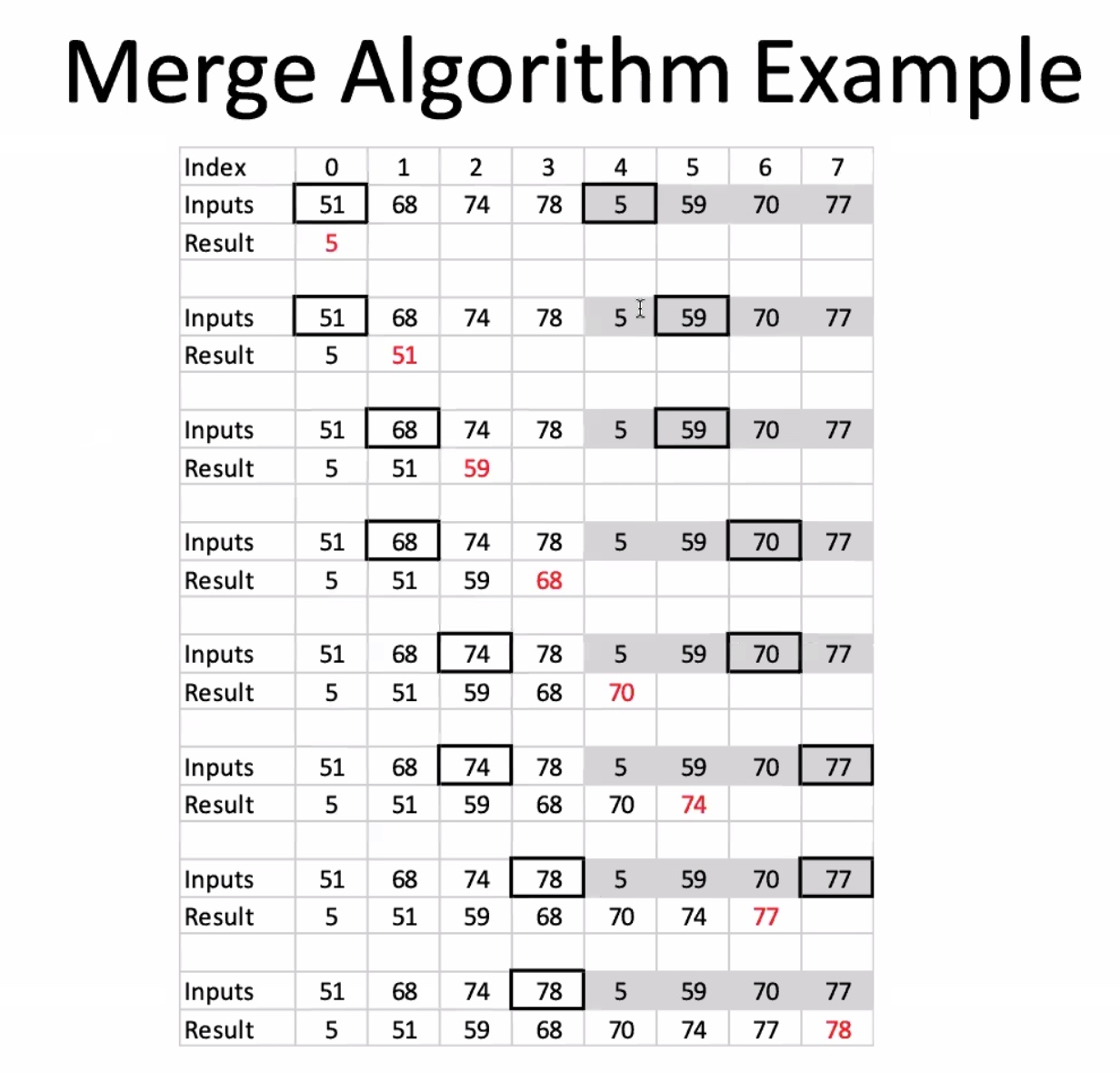

i is the cursor for the left array, j is the cursor for the right array. The first array is the first half of a and the second is the second half of a.
Lets assume hi - lo + 1.
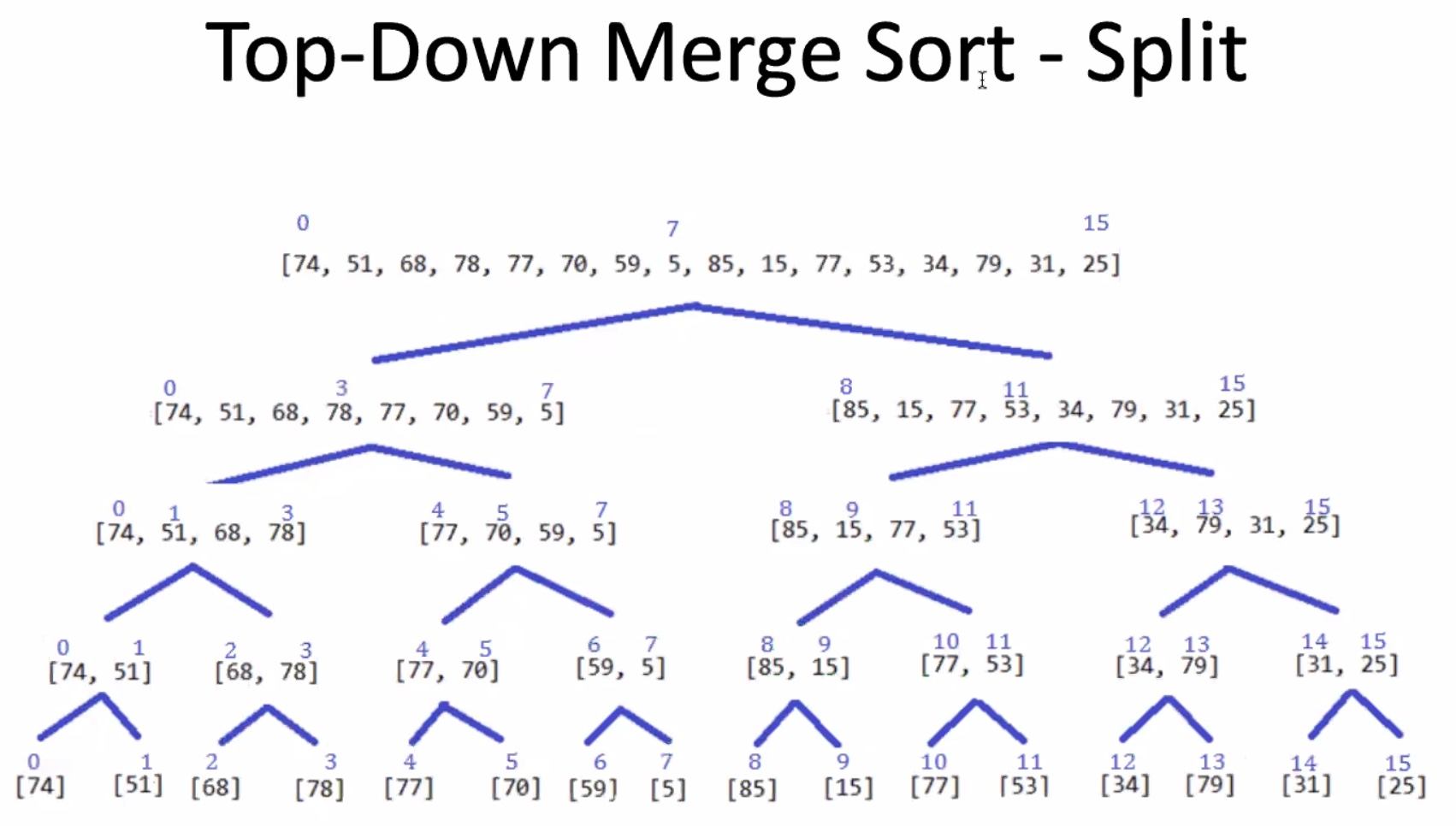
We split each array until each array only has 1 element. The reason for this is because an array with 1 element is sorted!


Lets analyze the space complexity. The recursive method is \( O(log(n)) \) . The first sort method is \( n + log(n) \) so it is \( O(n) \) .
Lets analyze runtime complexity.